基于贪心—线性规划算法的敏捷卫星观测时段选取

孙 慧，李 晖，赵 曼，张 超，应 文

(1.中国地质大学(武汉) 计算机学院，湖北 武汉 430074； 2.中国电子科技集团公司航天信息应用技术重点实验室，河北 石家庄 050081； 3.中电科海洋信息技术研究院(北京)有限公司，北京 100041)

0 引言

21世纪是我国全面发展的时代，经济、科学等方面的发展突飞猛进，航天技术方面也取得了一定的成绩。对地观测是卫星通过一定的传感装置对地球进行观测，获取地球表面信息并对其进行一定的处理过程。为了更有效地利用卫星资源，须结合实际任务需求进行资源的优化规划，即卫星任务规划。卫星技术不断发展，具有三维调整能力的敏捷卫星成为目前重要的对地观测卫星之一[1]，这使得卫星的观测较之前更为灵活和复杂，同时也意味着增加了任务规划的复杂性。在敏捷卫星任务规划中，当观测目标是点目标时，卫星对目标的实际观测时间比较短，不会占用整个可视窗口，因此，在敏捷卫星的任务规划过程中，还需要为每个点目标规划出观测时间段，即观测时间片段的选取问题[2]。

大多数卫星任务规划问题都是优化问题[3]，研究者采用各种优化算法对卫星任务规划问题进行求解[4]。许多研究表明，这些优化算法(例如差分演化算法)在解决卫星任务规划问题中凸显了自身的优势，得到了广泛应用[5]。因此，本文以差分演化算法为主要求解算法。在卫星任务规划过程中，存在很多约束条件，由差分演化算法直接迭代产生个体并不一定满足实际需求，需要对算法产生的个体进行冲突消解[6]，以满足卫星任务规划中的各项约束条件，该过程称为约束处理。本文在约束处理过程解决观测时间片段选取的问题，提出按最早可开始时间的贪心算法(以下简称贪心算法[7])和基于线性规划问题的求解方式(以下简称线性规划算法[8])进行求解，并将二者相结合，寻找出较好的求解方法。

1 敏捷卫星任务规划基本原理

1.1 敏捷卫星工作原理及对地观测过程

携带有传感器的敏捷卫星在围绕地球旋转的过程中以一定的姿态(俯仰、测摆和偏航)通过影像获取其星下点附近的地面信息，即卫星对地观测过程，如图1所示。卫星要获取的地面信息，即卫星的观测任务[9]。卫星对其星下点的观测可视范围，即可视时间窗口。

敏捷卫星运行包括许多复杂环节，其中对目标任务的图像采集是许多工作中十分重要的一个，其典型流程如下：首先明确观测目标与需求，确定观测任务的优先级和需求属性；对分级后形成的候选任务集进行任务规划，根据需求安排卫星资源；将确定好的规划过程转化为卫星控制指令；卫星根据程序指令执行相应的动作，完成成像工作[10]。

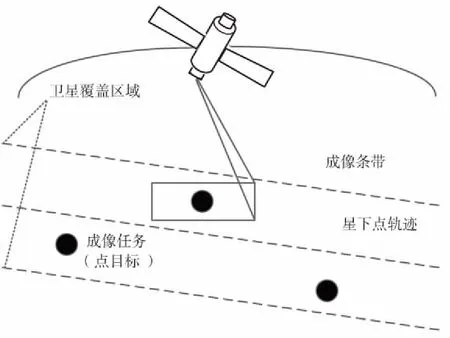
图1 敏捷卫星对地观测过程

1.2 敏捷卫星任务规划原理及过程

敏捷卫星任务规划就是在卫星成像之前，通过轨道方程计算，得出每个点目标的可视窗口(本文实验通过STK仿真软件计算[11])，然后通过各种算法，在满足各种约束的情况下，确定每个点目标的成像时间和观测顺序，得出满足需求的规划方案[12]。本文研究的问题是对点目标成像时间片段的选取，是敏捷卫星观测任务规划中的一部分，因此首先要实现对敏捷卫星观测任务的规划[13]。

卫星在对目标进行实际观测的过程中有很多约束条件，例如由于敏捷卫星对点目标的可视范围较大，窗口时间比较长，距离相近的点目标的窗口会出现重叠的情况，存在任务冲突；由于卫星工作需要指令控制，在一次观测过程中涉及一系列的指令如图2所示，因此在选片段的过程中要预留指令模板的时间，来避免指令模板冲突。此外，卫星的整个规划过程中还有许多约束要考虑，包括能量约束、单圈次观测时长约束和固存约束等。很多约束条件十分复杂，涉及到多个学科领域的专业知识，要将这些约束条件全部考虑进来会大大增加规划的难度。

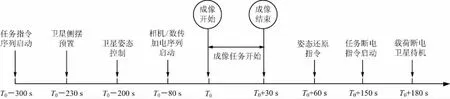
图2 卫星观测过程指令序列示意

本文所涉及的规划只包含观测部分，因此只考虑指令模板约束。指令模板冲突是指在2个连续观测任务之间时间间隔小于2个观测任务所需的指令模板时间之和，即在上一个任务的指令模板还未执行结束，下一个任务的指令模板却已开始。

1.3 敏捷卫星任务规划模型

一个观测可见时间窗口对应一个观测元任务。对需求中的每个点目标计算出对应的观测元任务，得到元任务集。选用差分演化算法对元任务集进行规划，并采取贪心—线性规划算法为每个元任务选择观测时间片段，以尽可能多地安排点目标。根据以上目标，建立任务规划模型的假设及约束变量的定义为：

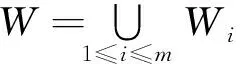
③ 观测元任务可视时间窗口的开始时间和结束时间分别用s，e表示，第j个元任务的窗口开始时间变量为sj，结束时间变量为ej；元任务的实际观测开始时间和结束时间用sa，ea表示，第j个元任务的实际开始时间为saj，实际结束时间为eaj；

④ 定义观测元任务决策变量x，如果元任务j能够完成，则xj=1，2…，反之，xj=0；

⑤ 侧摆所需时间用Tcs表示，单位为s；侧摆角度用c表示；指令模板间隔计算公式为：Tcs=k*c+d，k，d为常数，可以根据实际情况进行配置。对于连续侧摆10°与侧摆30°的模板间隔为(k*10+d)+(k*30+d)，对于n个元任务，指令模板时间间隔集合表示为Tcs=Tcs1，Tcs2，…，Tcsn；

⑥ 整个规划开始时间用TS表示，截止时间用TE表示。

基于以上的假设，建立相应数学模型：

(1) 规划目标

共有n个点目标要规划，为每个点目标选取合适的成像片段，使完成元任务数最多，表示方式如式(1)所示：

(1)

(2) 考虑约束

① 所有任务的窗口开始和结束时间必须在整个规划的时间段TS，TE之内，表示方式如下：

对∀j，1≤j≤n，满足

TS≤sj≤TE，TS≤ej≤TE。

(2)

② 所有的观测元任务的实际观测片段必须在观测可见时间窗口内，表示方式为：

对于∀j，1≤j≤n，满足saj≥sj且eaj≤ej。

(3)

③ 相邻2个观测元任务ai、aj之间的实际观测开始时间间隔不小于这2个元任务所需的指令模板时间之和，表示方式如下：

saj-eai≥Tcsi+Tcsj，∀i，j1≤i，j≤n，

assume： saj>sai。

(4)

2 基于差分演化算法的观测时间片段选取问题求解

基于差分演化算法在解决卫星任务规划问题上已有很多应用，本文使用差分演化算法作为任务规划的主要求解算法[15]。首先将卫星任务数据对应到染色体中，形成染色体种群；然后对每个染色体对应的元任务进行约束处理(冲突消解)，使得该染色体对应的解可行，本文在该过程中进行成像片段的选择；再对每条染色体进行适应值评价，并将当前代的最优染色体保存下来，然后通过差分演化算法迭代产生下一代种群，重复上面的步骤，直到迭代结束，选出最优的染色体，最后对最优染色体进行解析，对应到卫星规划问题中，得出每个点目标的成像片段，并得出规划的点目标数[16]。算法规划流程如图3所示。

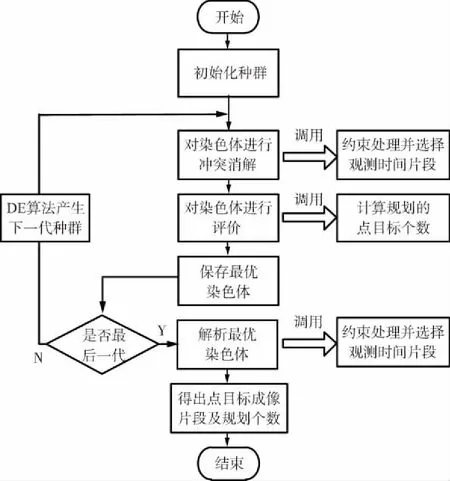
图3 算法规化流程

2.1 基于最早可开始时间的贪心算法选择成像片段

为了规划完成的任务数最大，在选择成像片段过程中，需要尽可能地避免模板上的冲突。本文采用的贪心算法就是通过调整观测元任务所选取的成像片段来减少它对其他任务的影响[17]。

选择成像片段的算法实现过程如图4所示。首先将观测元任务按照窗口时间先后进行排序，选取每个窗口的最后时间片段作为初始选择；由于没有其他任务的限制，可将第一个元任务的时间片段调整到可视窗口的开始位置；然后按顺序获取下一个元任务，判断该任务与上一个任务是否有指令模板冲突，如果有则删除该任务，如果没有，则调整该元任务的观测开始时间；继续上面的步骤，获取下一个元任务，选择时间片段，直到所有的任务都遍历完，则结束选成像片段过程。

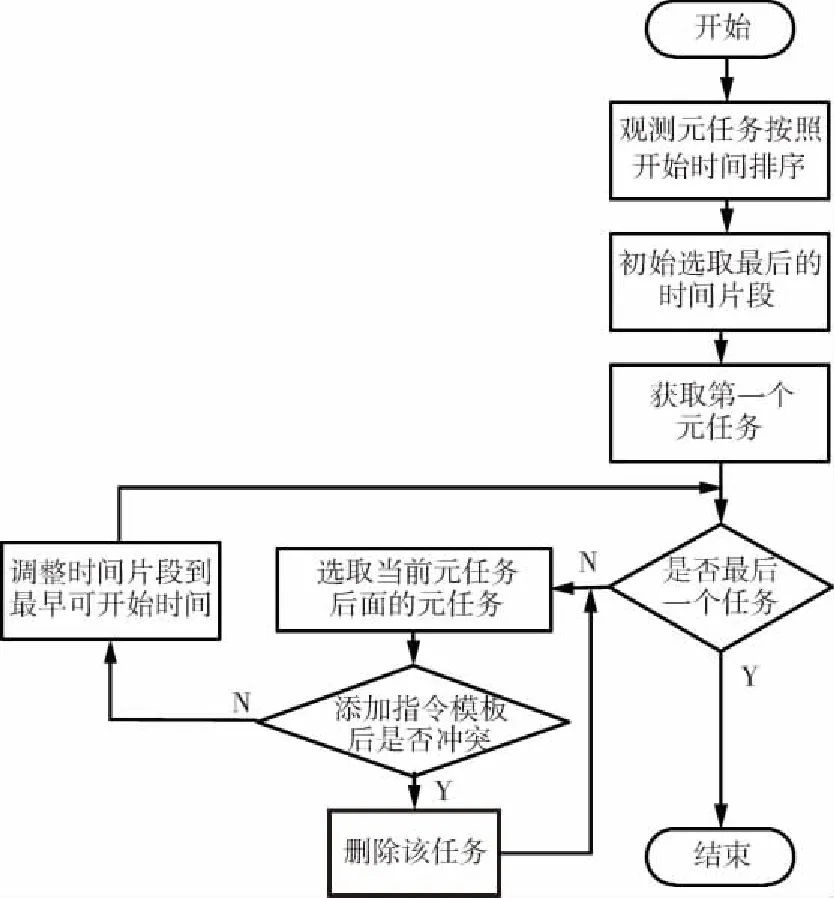
图4 基于最早可开始时间选择成像片段的贪心算法流程

在上述流程中，主要通过判断是否有指令模板冲突来调整观测时间片段，具体过程如图5所示。

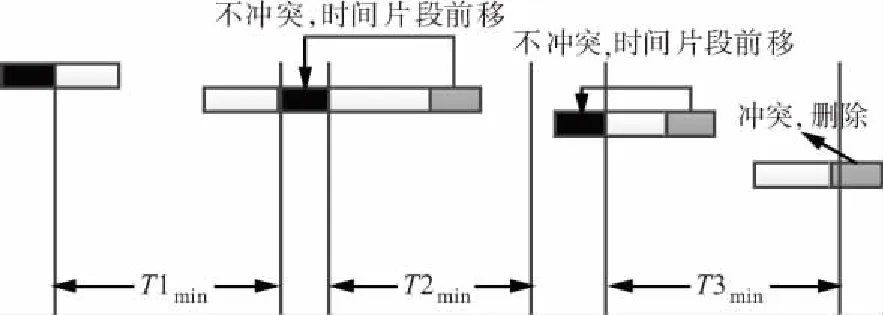
图5 调整成像片段示意

从图5中可以看出，从左到右有4个点目标，分别记为目标1、目标2、目标3和目标4，这些目标的顺序按其可视窗口的时间先后而定，假设目标1是当前一批目标中可视窗口最早的目标，点目标要求的观测时长为t。对于每个观测元任务，初始时均选取可视窗口的最后t时段作为选取的成像片段，如图5中的灰色部分；该窗口开始时间是观测的最晚开始时间，否则不能满足观测时长要求。然后根据约束，进行成像片段的调整，如图5中的黑色部分，调整顺序按窗口排序依次进行。对于当前批的第1个元任务，其时间片段的选取不会受前面元任务的影响，因此可将成像片段调整到窗口开始t时段。

然后对第2个元任务进行调整，处理方法是在第1个元任务选中的成像片段结束时间加上该任务的结束指令模板时间和第2个任务的开始指令模板时间，得到一个允许的最早开始时刻t1。t1时刻存在的区间有3种情况：① 晚于第2个任务的窗口开始时间但早于第2个任务初始选中片段的开始时间；② 早于第2个任务的窗口开始时间；③ 晚于第2个任务初始选中片段的开始时间。针对以上3种情况的调整情况是：将时间片段调整到t1时刻；将时间片段调整到窗口开始时刻；删除任务。分别对应图5中的目标2、目标3和目标4。

2.2 基于线性规划问题的求解方法选择成像片段

线性规划问题是在一系列线性约束条件下，对目标函数求最优解的过程[18]。由此可将求解线性规划问题的方法应用到卫星任务规划中，以此来选出点目标合适的观测时间片断[19]。要运用线性规划的解决算法，首先要对卫星规划问题采用线性规划问题的建模方式进行模型的建立[20]，在本文的研究中，主要考虑的约束条件是时间窗口约束和指令模板约束，即元任务的实际观测时间要在可视窗口的时间范围内，观测元任务之间的时间安排要符合指令模板约束。假设每个点目标的观测时间只需要5 s，以上约束关系可表示为：

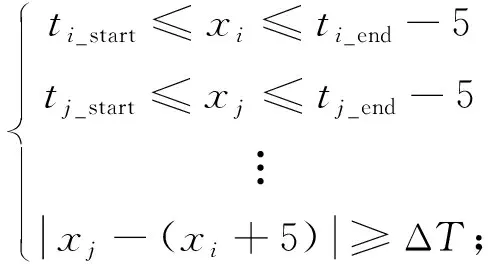
(5)

式中，xi和xj分别表示第i和j个观测元任务的实际开始观测时间，xi≥0，xj≥0且j≠i；ti_start和ti_end分别表示第i个观测元任务某个可视时间窗口的开始时间和结束时间；ΔT表示元任务i和元任务j之间指令模板间的时间间隔。

但是上述约束条件不能运用线性规划的求解方式来求解，因为线性规划问题中，线性约束条件之间是相与的关系，即所有的关系必须同时满足[21]。而式(5)中存在相或的关系，因此，对卫星规划中的约束条件做如下改进，即

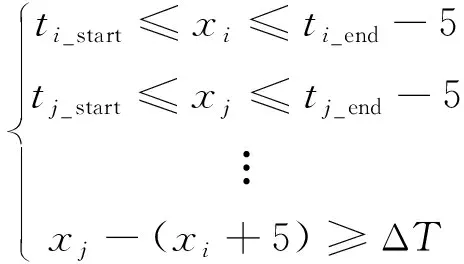
(6)

式中，xi≥0，xj≥0且xj>xi。

式(6)在式(5)的基础上进行一定的修改，去掉表示指令模板约束的式子中的绝对值，并且要求xj>xi，即任务j的实际观测开始时间早于任务i的实际观测开始时间，这意味着假设存在某一个可行的规划方案，任务j可以安排在任务i之后进行，但这个规划结果会被线性规划解决方法遗漏，可能会使线性规划得到的解并不是卫星规划中的最优解。虽然存在上述的不足，但是在单纯形算法解决线性规划问题的时候，如果问题有解，那么找到的一定是最优解。针对这一特性，利用线性规划的思想解决卫星规划问题还是有一定研究意义的。

在确定好约束条件后，需要构造对应的目标函数。卫星规划的优化目标是一次规划安排的点目标的个数，对应到线性规划问题中，就是当目标函数有解时对应的x个数[22]。由此发现，实际目标函数是X={x1，x2，x3，......xn}，其中，X中xi的个数最多，即最多个点目标被规划。但是，该目标函数无法用线性公式表示，不符合线性规划要求。因此，构造式(7)所示目标函数，当该目标函数有解，即实际目标函数达到最大值。

ymin=x1+x2+x3+x4+x5+…+xn，

(7)

式中，n为所有点目标的个数。

根据以上目标函数，当目标函数有解时，对应x的解即可得到每个点目标的成像片段。

当构造的目标函数无解时，意味着在该约束条件下，目标函数中涉及的x变量所对应的点目标不能全部被安排[8]。需要删除某些点目标，重构目标函数。

本文引用冲突量概念作为删除依据，计算每个点目标与其后目标的窗口冲突时长，冲突时间越长，冲突量越大。删除冲突量最大的点目标，继续上述规划算法，求最优解。重复上述过程，直到目标函数有解。

3 实验测试与分析

算法的参数会一定程度上影响算法的计算效果。在实验过程中，要根据不同的实验数据规模来确定算法参数。本文测试过程中选取了不同数据量的测试实例对算法进行测试，选取了以下2类具有代表性的测试用例对测试结果进行分析。2个测试实例的元任务数及参数设置如表1所示。

表1 测试实例元任务个数及差分演化算法参数设置

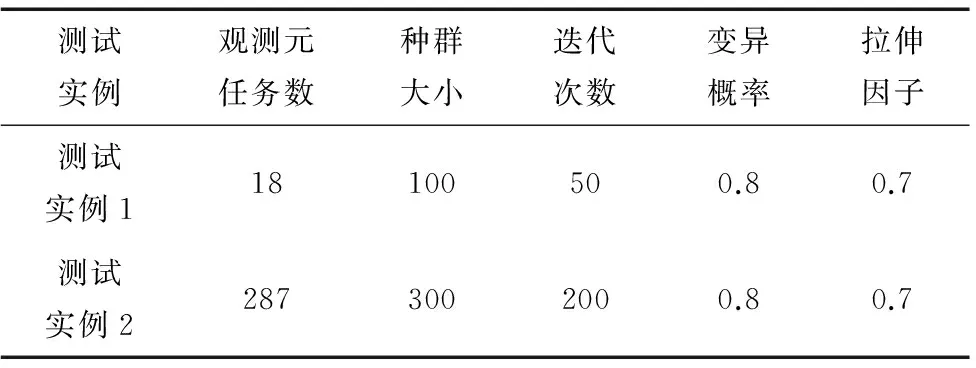
测试实例观测元任务数种群大小迭代次数变异概率拉伸因子测试实例118100500.80.7测试实例22873002000.80.7

3.1 规划结果对比分析

本文中的实验对基于最早可开始时间选择观测片段的贪心算法和基于线性规划选择时间片段的算法进行了组合测试，即在程序设计上，将这2个算法可以分别运用到2个地方：① 在差分演化算法迭代过程中，在每次迭代中运用上述之一的算法进行成像片段选取及指令模板约束处理；② 在迭代结束后对选择出评价结果最好的染色体进行解析，计算出成像时间片段。

对2个算法进行组合，共有4种实验方案：

① 基于最早可开始时间的贪心算法(G)+基于最早可开始时间的贪心算法(G)；

② 基于最早可开始时间的贪心算法(G)+基于线性规划问题的求解算法(L)；

③ 基于线性规划问题的求解算法(L)+基于最早可开始时间的贪心算法(G)；

④ 基于线性规划问题的求解算法(L)+基于线性规划问题的求解算法(L)；

在上述4项选择中，“+”前面表示在差分演化算法迭代过程中运用，“+”面表示在最后解析最优染色体过程中运用。

2组测试实例针对4种实验方案的规划结果(即安排的点目标个数)对比如表2所示。

表2 结果对比表

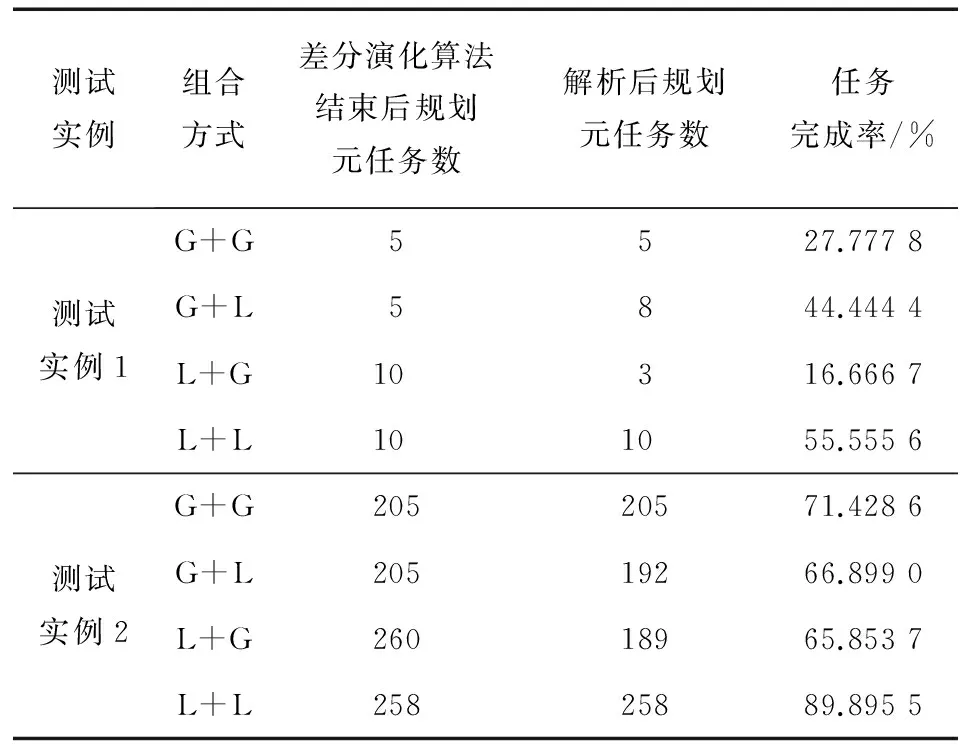
测试实例组合方式差分演化算法结束后规划元任务数解析后规划元任务数任务完成率/%测试实例1G+G5527.777 8G+L5844.444 4L+G10316.666 7L+L101055.555 6测试实例2G+G20520571.428 6G+L20519266.899 0L+G26018965.853 7L+L25825889.895 5

根据以上测试结果可以看出，在第1组测试实例中，方案基于线性规划问题的求解算法+基于线性规划问题的求解算法(L+L)的规划结果最好，完成任务率最高，其次是方案②、方案①和方案③。通过对比可以发现，在解析最优染色体阶段使用线性规划的解决方法一般可以规划较多的任务数，并且可以优化贪心算法得出的结果；而用贪心算法解析线性规划得出的最优染色体则会使原本的结果变差。如果单纯某一种算法，没有优化的效果。

在对测试实例2的大量实验过程中，大部分实验结果符合上述针对测试实例1的实验结论，但也存在一些结果并非与上述结论完全一致，如表2中关于测试实例2的结果中，方案②在解析阶段使用线性规划求解问题的方法并没有得出像测试实例1中的优化效果，这是由于线性规划处理阶段存在随机性，有时会有优化效果，有时效果反而变差。因此，在实际规划过程中，可以先采用贪心算法得出规划结果，然后用线性规划求解算法进行解析，如果结果变好，则用优化后的规划结果，如果没有优化，则用之前的规划结果。因此，说明采用线性规划的算法是一种可选的优化方案，但得到的结果并不一定是最优的，在实际应用中，可以将线性规划的结果作为一个参考项与贪心算法结果进行比较，择优选择解决方法。

3.2 规划时间及算法收敛性对比分析

与上述实验方法相同，对2组测试实例在运行时间和算法收敛性方面进行分析总结。2组实例的时间对比情况如表3所示。

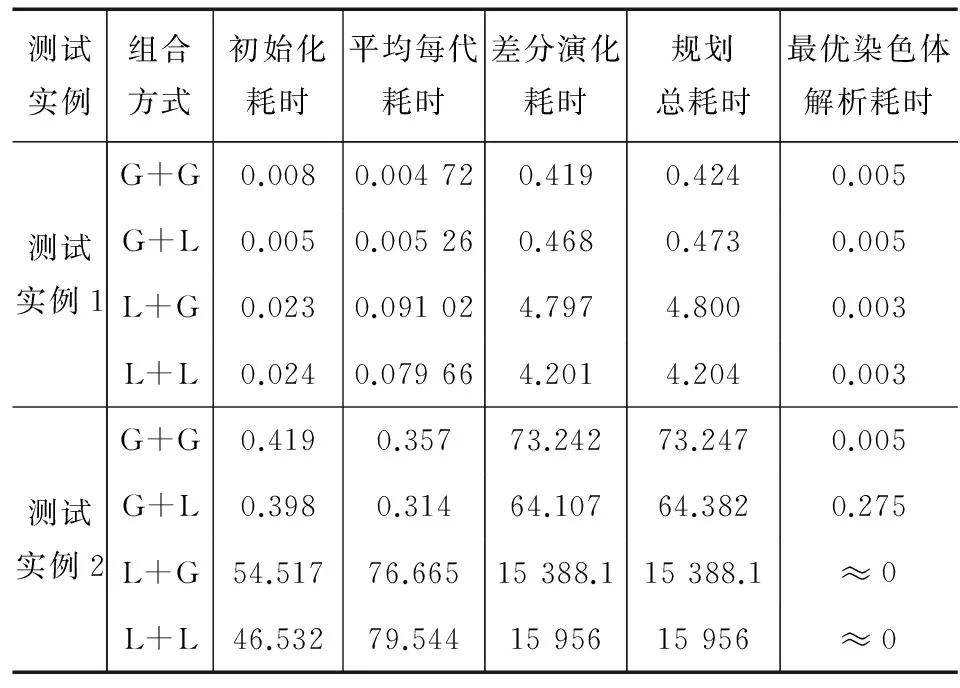
表3 各项运行时间对比 (s)

由表3可以看出，在整个规划过程中，差分演化算法迭代会占用较多的时间，解析过程所占的时间比重十分小；线性规划算法耗时比较长，贪心算法耗时比较短。因此，一般只在解析阶段使用线性规划对结果进行优化，不会用到演化过程中，而贪心算法在演化过程中的效率比较高。

对2组测试结果进行对比分析可以得出，在数据量小的情况下，在差分演化算法过程中使用线性规划算法的耗时还在一定的可以接受范围内，但当数据量即要规划的点目标个数增大时，线性规划的耗时对整个算法的运行效率影响很大，在实际工程应用中是无法接受的，这也说明线性规划使用在差分演化算法过程中是不适用的，只适合最后的优化选项过程。

对测试实例2进行收敛性分析，分别用方案①(贪心算法+贪心算法)和方案④(线性规划算法+线性规划算法)的规划组合进行实验，2种不同的策略对应差分演化算法的收敛情况如图6所示。

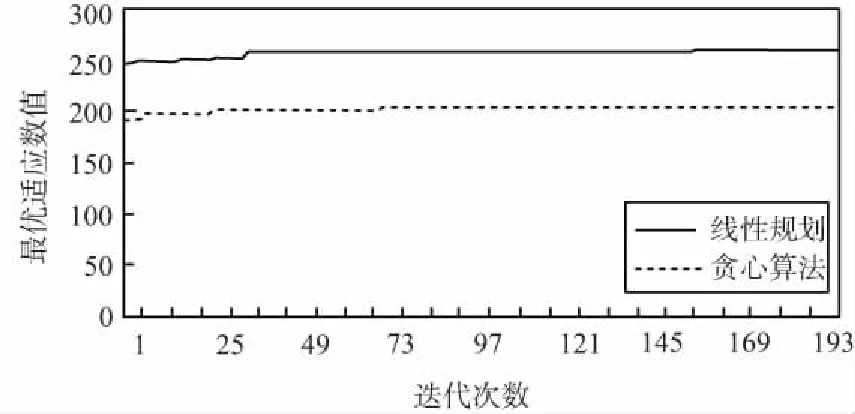
图6 2种策略收敛情况对比

由图6可以看出，贪心算法在100代左右收敛，而此时线性规划还在优化过程中，直到160代左右收敛，由此可见，二者收敛速度都较快，贪心算法比线性规划算法使差分演化算法收敛相对更快些。

3.3 实验结论

结合上述对规划结果、运行时间和算法收敛速度3个方面的对比测试可以发现，在选择成像片段的过程中，如果采用线性规划的解决方法则可以较多地规划任务数，但是线性规划的耗时十分长，是贪心算法的10倍以上，会影响整个程序的性能。相比之下，贪心算法收敛速度快并且耗时少；在选择成像片段的过程中，为了能够尽可能多地规划任务并且使耗时在可接受的范围内，可以将耗时少的贪心算法运用到差分演化迭代过程中来选择最优染色体，在得出一个结果后，选择线性规划方法尝试优化，如果结果比原来的好，则采用该方法选片段，否则，维持原来已有的结果。

4 结束语

本文提出基于贪心—线性规划相结合的方式进行敏捷卫星任务规划过程中观察时间片段的选取。在差分演化算法迭代过程中采用贪心算法可以比较快速地得出点目标的成像片段，在解析最优染色体的过程中采用线性规划算法多数情况下可以优化规划结果，安排更多的点目标。该方法提高了整个卫星规划的效果，更好地利用卫星资源，有着很好的研究价值和应用前景。