基于BLT方程的线性传输线网络自动化分析

罗文君，赵 翔

(四川大学 电子信息学院，四川 成都 610064)

0 引言

在设计和分析电子系统时，通常需要分析其在复杂电磁环境中的工作状况和电磁兼容性，其中一个重要部分是对系统中传输线网络(Transmission Line Network，TLN)受到的电磁干扰进行分析评估。通常在低频情况下对线缆网络的建模分析是采用电路理论，而高频情况下由于波的传播特性受电尺寸影响较大，低频电路理论不再适用，主要采用时域有限差分法、矩量法、有限元方法和BLT方程方法等[1]。其中全波分析方法的时空开销相对较大，在对大型的传输线网络进行分析时，基于电磁拓扑理论和BLT方程方法计算效率更高。

电磁拓扑学概念最先由Baum等人在1974年提出[2]，从此应用于分析复杂电磁交互环境的问题上[3-4]；1978年，Baum等基于之前研究推导出了BLT方程，接着网络BLT方程也逐渐得到推广[5-6]；同年，Liu等人基于相关理论开发出了软件QV7TA，美军方曾经将其应用于飞机、导弹和人造卫星等的设计，1997年法国航空航天局(ONERA)的科学家也开发出可进行宽带传输线分析的软件CRIPTE，这2种软件的相同点在于均是在频域中对BLT方程进行求解[7]。在国内，相关研究主要涉及基于BLT方程的传输线网络理论分析[8-14]，但相应的自动化分析技术和外场辐照下TLN分析的研究鲜见。

本文研究目的在于提出并实现对线性TLN在辐射和传导干扰情况下响应的自动化分析技术。首先，对于一个一般性的线性线缆网络结构，应用电磁拓扑方法，将其中的线缆结构等抽象为管道(Tube)，线缆之间的器件负载等结构抽象为节点(Node)，从而降低干扰源和受干扰对象们之间的电磁耦合复杂度，最后建立其BLT方程进行计算分析。然后，在自动化实现上述过程时，基于面向对象编程理念(Object Oriented Programming)，对所给线性TLN的数据信息进行数据解析、参数保存和网络BLT方程的构造并求解[15-19]。最后以典型的树形和环形网络为例，分别在辐照和传导激励的情况下求解网络端口的时域和频域响应，并通过与基于全波分析方法的软件的对比，去验证本文自动化分析技术的有效性和准确性。

1 BLT方程的建立和求解

应用电磁拓扑理论，复杂的线性TLN可以看作一个只有节点和管道的拓扑网络结构。

假设一个拓扑网络结构中有n个管道、m个节点。要对网络结构中的2n个端口求解响应时，由BLT方程可以推导出十分简洁的矩阵形式：

(1)

式中，VL，IL分别为网络的端口总电压和总电流超向量；Vs为激励源超向量，它们均为如式(2)所示的2n维列向量。式(2)中VL、IL，Vs下标的i1和i2分别代表第i号管道2个端口的编号；Γ为2n×2n的传播超矩阵，代表网络中所有管道的传输参数；ρ为2n×2n的散射超矩阵，表示网络中所有节点的散射参数；Ι为2n×2n阶的单位超矩阵；Yc为节点导纳矩阵，即

(2)

当采用集总电压源V0或电流源I0作为管道上的传导激励源时，沿线等效电压源计算公式为：

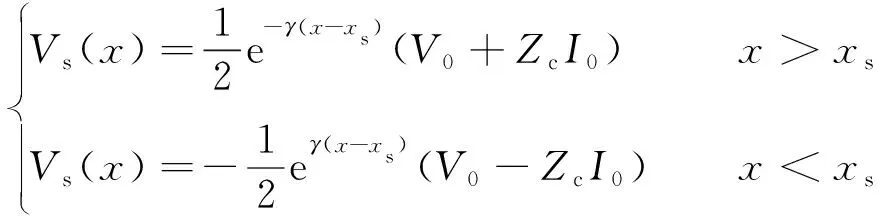
(3)

式中，Zc为管道的特征阻抗；γ为传播常数；xs为集总源在管道上的位置。

当采用外电磁场辐照激励时，未屏蔽的传输线会在整条管道上产生等效分布源。以理想导体地面上高度为h、长度为L的一段单导体传输线为例，分布源计算公式为：

(4)

这种情况下，管道的等效源矢量为：

(5)

BLT方程中的散射超矩阵ρ由各节点的散射参数和网络结构决定，是一个2n×2n的矩阵。一个典型树形TLN拓扑图如图1所示，其中，N代表节点，T代表管道，P代表端口。

图1 一个典型的树形网络拓扑图

根据网络散射矩阵的定义：Vref=ρVinc，对多端口的节点如N2，散射系数即其S参数；对于单端口的结构，如N1，N3，N4，当终端阻抗为ZL，

(6)

图1中的网络散射超矩阵为：

(7)

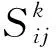
Γ为2n×2n的传播超矩阵，包含网络中所有管道的传输参数，它是一个对称矩阵。管道间的电压和电流波按照e-γiLi指数规律传播[1]，Li代表第i号管道的长度，这个管道的传播矩阵为：

(8)

整个网络的传播超矩阵为：

(9)

将以上求得的源矢量、散射超矩阵和传播超矩阵代入BLT方程的一般形式，即可求得在此频点下网络中各个端口的电压电流值。

2 线性TLN分析的自动化实现

为了实现自动化的构造并求解线性TLN的BLT方程，采用如图2所示流程图完成以下几个部分工作：对用户输入的TLN拓扑结构数据进行读取和预处理；通过对数据的解析，建立各类超矩阵，构造网络BLT方程；处理激励信号，对其时域波形运用FFT变换，获取频域信号值；对各频点分别构造激励源向量，代入网络BLT方程，得到当前频点下的各端口响应；对每个端口的完整频域响应运用IFFT计算得到其时域响应；时频域响应结果输出。

在进行自动化分析程序的开发时，采用面向对象编程理念(Object Oriented Programming)进行程序总体架构的设计，将各种物理对象进行封装，构建相应的类(Class)[15-17]。例如，通过将管道自身参数和其端接节点信息进行封装，构建Tube类；将节点自身参数和其端口所连管道信息进行封装，构建Node类。这种封装方法能够高效并直观地管理数据，方便添加、删除和修改拓扑结构中的节点和管道信息[18-19]。

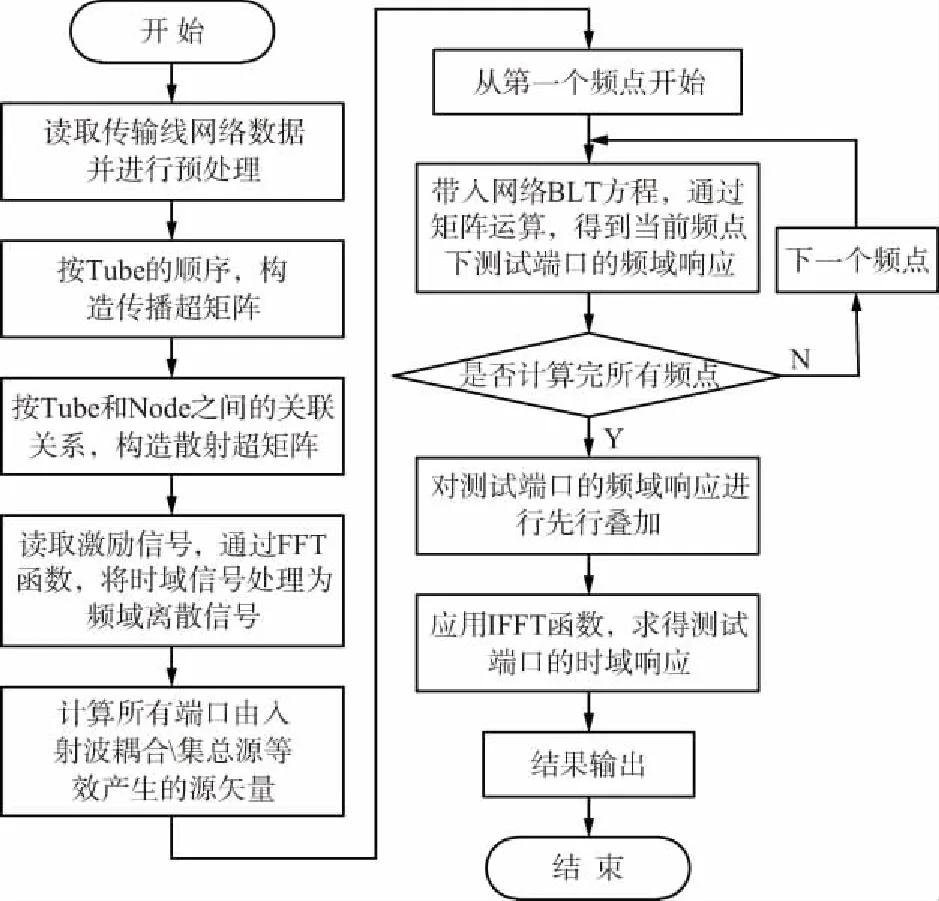
图2 程序流程

3 算例及验证

针对若干常见网络，以树形和环形结构TLN为例进行分析，网络距地面高度0.1 m。

3.1 算例1：传导激励下的线性TLN

激励信号波形如图3所示，网络拓扑结构如图4所示。采用双指数脉冲作为激励信号，作用于一个Y状的树形线性TLN上，信号从Port1端输入，设置2个测试端Port2和Port3。

图3 激励信号波形

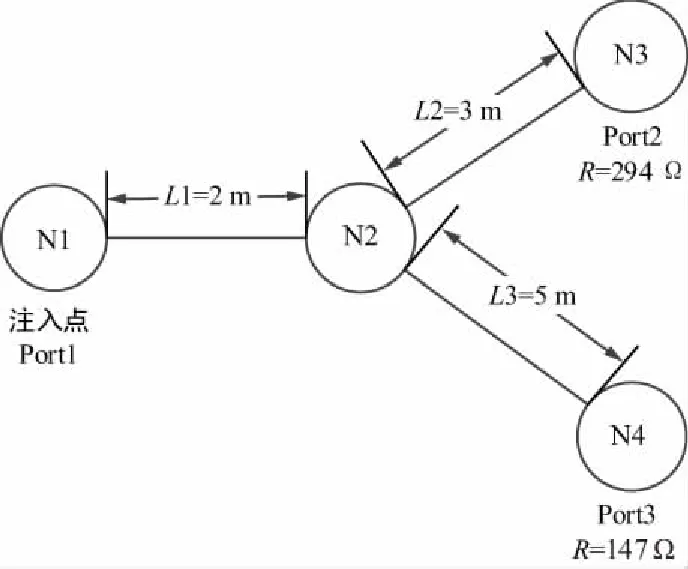
图4 树形结构的线性TLN拓扑模型

3个端口的时域响应与全波分析软件计算结果的对比如图5所示。3个端口频域响应归一化值的曲线如图6所示。

图5 3个端口的计算和验证的时域对比

图6 测试端口的频域计算结果

一个环形结构TLN如图7所示。在相同激励情况下对环形结构线性TLN进行计算。

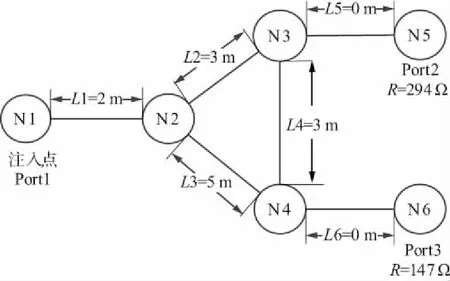
图7 一个环形结构TLN

3个测试端口的时域响应与全波分析软件计算结果的对比曲线如图8所示，3个测试端口频域响应归一化值的计算曲线如图9所示。

图8 3个端口的计算和验证的时域对比

图9 测试端口的频域结果

图5和图6中分别比较了2种网络的3个端口的时域响应结果，可以看出验证结果和计算结果吻合良好，从而验证了本文所采用自动化技术和程序的有效性和准确性，并且在同样计算机配置情况下，全波分析软件对2种网络结构的计算时长均在5 min以上，本文方法在保证准确度的情况下，对2种网络的计算时长分别为0.24 s和0.29 s，体现了方法的高效性。

3.2 算例2：辐照激励下的线性TLN

将具有和算例1相同拓扑结构的线性TLN，置于图10所示的辐照激励环境中。选择一个频率为200 MHz的正弦平面波作为激励，入射方向与xoy平面夹角为60°，与x正方向夹角为180°，电场极化方向平行于入射面。

3个测试端口的时域响应与全波分析软件计算结果的对比曲线如图11所示。

可看到仿真验证中3个端口输出的正弦波信号与本文自动计算得到的结果基本吻合，证明了方法的有效性和准确性。

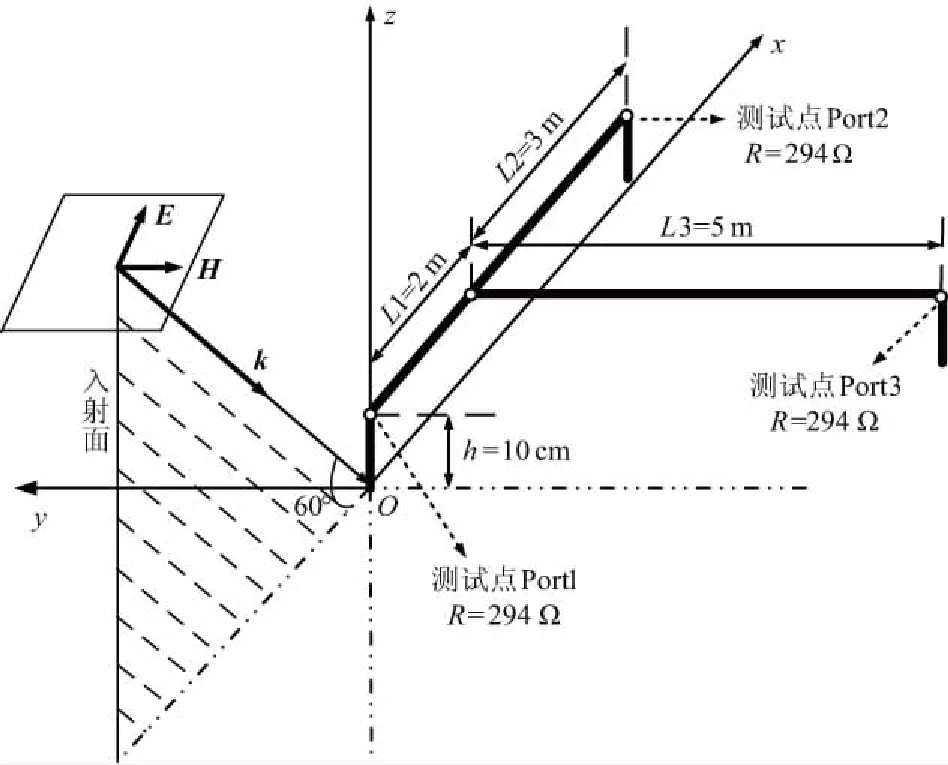
图10 辐照激励下的树形线性TLN

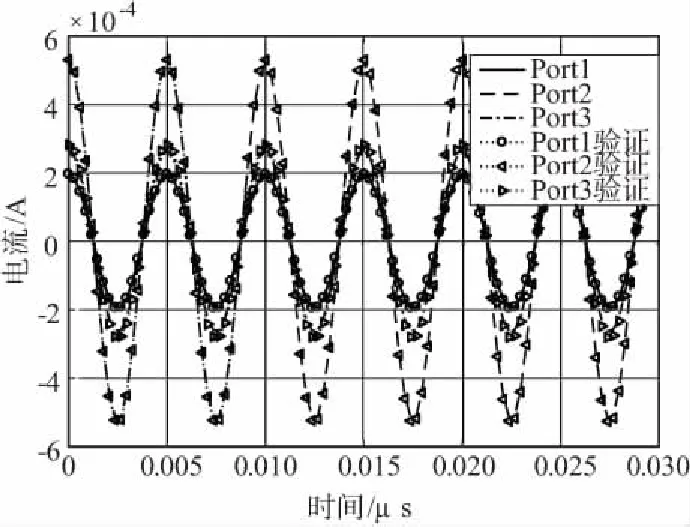
图11 3个测试端口的计算和验证的时域对比

进一步对更复杂的激励信号和更复杂的线性TLN拓扑结构案例进行计算。将辐照的连续波信号换如图12所示的电磁脉冲(EMP)信号。

图12 一个EMP激励信号

对算例2中的树形线性TLN进行计算得到的3个测试端口分别在时域和频域的响应曲线，如图13所示。

图13 3个测试端的响应输出

在相同的EMP激励信号下，将树形线性TLN换成更复杂的环状网络，如图14所示，并进行计算。

图14 EMP辐照下的环形线性TLN

计算得到的3个测试端口分别在时域和频域的响应曲线如图15所示。

通过上述算例可以看到，本文的自动化分析程序可以对多种拓扑结构的TLN进行集总源和外场辐照激励下的时、频域响应分析。

图15 3个测试端的响应输出

4 结束语

本文实现了对线性TLN在辐照和传导2种激励方式下响应的自动化评估。上述算例结果不仅证明了自动化分析的准确性和有效性，并且计算速度突显优势。这是因为电磁拓扑理论结合面向对象理念，对于分析复杂的网络和复杂的激励，起到了简化模型和减少计算量的作用；自动化处理过程对较大型网络的分析具有优越性；快速傅里叶变换和反变换能高效地完成对激励信号和响应结果在频域和时域上的转换。需要注意的是，该方法只适用于线性条件下的TLN分析，因为线性条件的TLN才能线性叠加各频点的响应。