基于机器人折弯应用的运动规划
■ 张涛

扫码了解更多
进入21世纪以来,工业机器人已广泛应用在汽车、电子、金属、化工、食品等各大领域,从事着诸如搬运、焊接、冲压、装配等工作,大幅减少了人工劳动成本,提高了生产效率。而随着制造业的快速发展,钣金件在机床、电气、厨具及门业等领域中的应用越来越多,折弯则是一种重要的钣金成形方法。
目前,机器人折弯已引入到折弯行业中,但人工辅助的方式仍较为普遍,这就造成了折弯的一致性低、可靠性差等多种问题。机器人全自动折弯系统,可以保证折弯工艺的一致性和可靠性,国内外学者也进行了大量的研究工作。这样的系统无需人工介入,由机器人完成取件、对中、折弯、放件等一系列动作,而折弯机的动作通过与机器人建立的通信来进行。
在折弯过程中,由于折弯机和机器人是两套独立的设备,仅通过PLC来交换信号,但机器人需要抓取着工件,并伴随折弯机上模的动作来做出跟随动作。如果动作提前或动作滞后,将会使工件发生变形从而成为废料,并在一定程度上会损坏折弯机模具、机器人手爪,甚至机器人本体。
如何使机器人和折弯机能够完美的配合完成折弯,是机器人行业和折弯机行业研究的重要课题。
一、机器人折弯系统
1. 系统组成
机器人折弯系统主要由以下几部分组成:机器人、折弯机、重力对中台、吸盘手爪、上下料台等,如图1所示。
吸盘手爪安装在机器人手腕上,负责对工件抓和放。机器人将工件从上料台上抓起,移动到重力对中台上方将工件放下,再重新抓起来,保证抓取位置的一致性。然后机器人带着工件移动到折弯机的下模上方,开始跟踪折弯。待折弯完成后,机器人带着工件离开折弯机,移动到下料台并放下工件。以上是只对一道工序折弯的流程描述,实际生产中每个工件的折弯工序一般会有很多道,期间会进行工件的换向等操作。
除折弯工艺外,其他点位通过人工示教完成,这样机器人执行程序可自动完成工件取料、定位、折弯、放料,并加工出需要的产品。

图1 折弯系统组成
本文重点探讨折弯工艺中的机器人跟随问题。
2. 折弯工艺描述
折弯工艺分为以下步骤:
机器人带动工件至折弯机下模具上方,工件完全贴合下模具,此时机折弯机上模具位于上死点,也就是说折弯机是静止不动的,如图2a所示。
折弯机起动,上模具快速向下运动,且运动至变速点,此过程机器人保持不动,如图2b所示。
折弯机上模具以慢速从变速点移动到夹紧点,此过程机器人依然保持不动,如图2c所示。
折弯机上模具以慢速继续往下运动,此时机器人带动着工件做出相应的动作,直到上模具达到下死点,折弯完成,如图2d所示。
上述过程完成后,上模具快速往上运动到上死点,同时机器人带着工件退出折弯机工作区域,完成该道工序的折弯。
3. 机器人跟随方案
在折弯过程中,机器人的跟随方案一般分为两种类型:开环和闭环。开环是根据折弯过程中的几何模型,预测折弯机上模具位置和机器人本体姿态的关系,预先生成机器人的运动路径,这种方式可以保证机器人的运动速度,且不受额外硬件的限制。闭环则需要额外的模块,如编码器、光栅尺等可以实时捕获折弯机上模具位置,然后通过折弯几何模型,实时计算出机器人应该到达的位置并反馈给机器人,机器人再做出相应的动作以匹配折弯机上模具的位置。但这种方式需要一定的成本,跟随速度难以保证,跟随效果可能会遭遇延迟。
本文讨论的机器人跟随方式为开环,流程如图3所示。
二、坐标系确定
在开始几何模型分析之前,首先需要对坐标系做出明确规定。机器人的工具坐标系(工具坐标系是定义工具中心点位置和工具姿势的坐标系)的值需要尽可能准确,而用户坐标系(用户坐标系是用户对每个作业空间进行定义的直角坐标系)需要建立在折弯机下模具表面,原点位于折弯机下模具槽口的中心线上,Z轴竖直向上,Y轴指向机器人所在位置。
如图4a、图4b所示,用户坐标系Z轴竖直向上,Y轴指向机器人,X轴根据右手定则确定。图4c是机器人安装了TCP针在建立用户坐标系的过程,此时针尖正处于折弯机下模具槽口的中心线上。

图2 折弯工艺过程

图3 开环方案流程
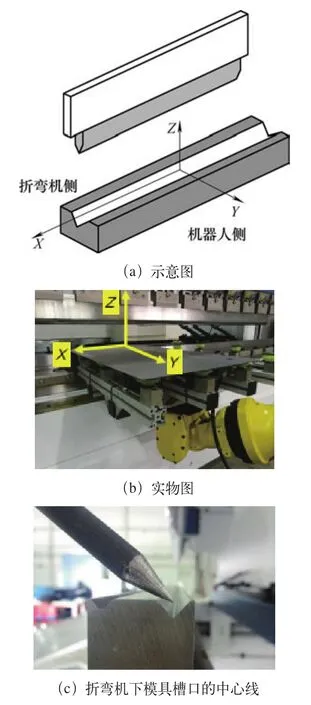
图4 建立用户坐标系
三、几何模型分析
1. 建立几何模型
在图4a、图4b的Y轴和Z轴构成的平面上,建立几何模型,如图5、图6所示。
其中:O点为折弯机下模具的上端倒角的圆心,Rsm为其倒角半径。O´为上模具(即刀具)的倒角圆心,Rp为其倒角半径。2α为下模具的角度。H为下模具的上表面到最低端的深度。h为当前工件的下表面距离下模具的上表面的深度。T为折弯工件的厚度。角度a为O和O´连线与水平线的夹角。角度b为O和O´连线与工件方向的夹角。θ为工件方向与水平线的夹角,且有θ=b-a。
2. 几何模型计算
目的要计算出h和θ的关系,首先要计算的是O与O´连线的长度。
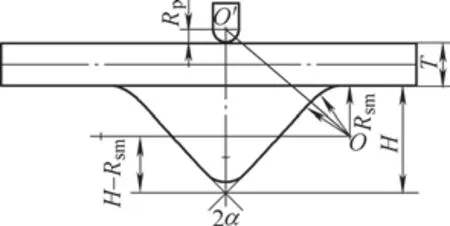
图5 折弯开始前模型
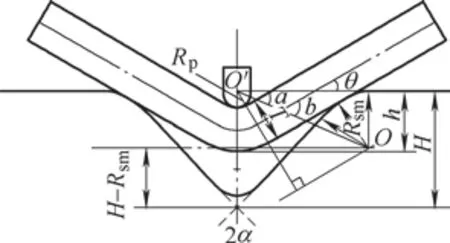
图6 折弯过程中模型
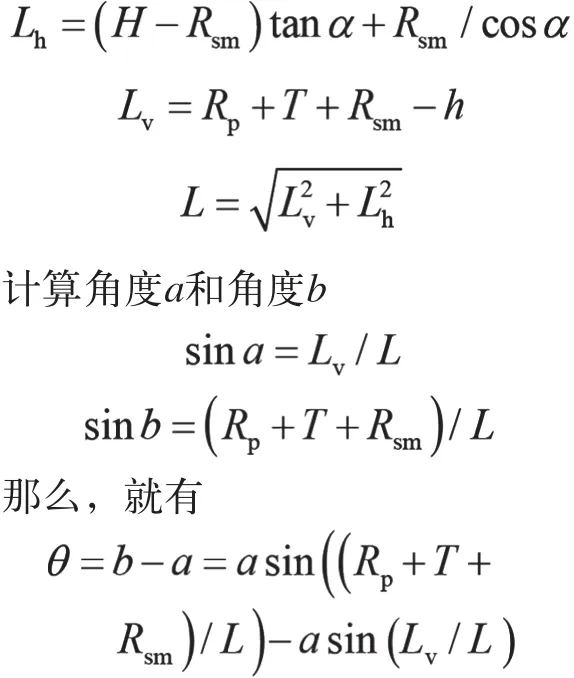
接着来计算折弯时动态点U的位置变化,如图7所示。
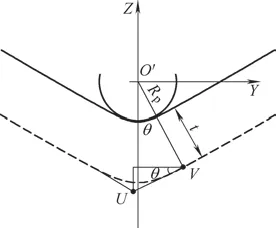
图7 折弯动态点
设中性层厚度为t。由于折弯前中性层与Z向的交点U会随着折弯过程发生位置变化,故该交点U的坐标与折弯角度θ有关。
根据图7中的几何模型,V点为O´点到中性层的垂足,当θ=0时,U点与V点重合。折弯拉伸引起的U点与V点之间的距离,可近似为

考虑到原点O´的坐标也是在变化的,且初始位置将会建立在中性层上,故Uz的值需要加上Rp+t-h,因此修正Uz为:
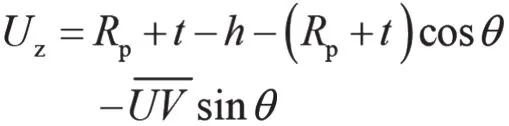
至此,Uy、Uz和θ将构成折弯过程中机器人姿态的三个元素。
除参数h外,其他的输入参数都是已知的,故θ是关于h的函数,即:
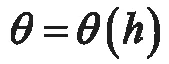
而对Uy、Uz来说,它们只和θ、h有关,也就是只和h有关,即:
简而言之,当h不同时,Uy、Uz和θ就不同,机器人的姿态也就不同。
3. 模型检验
当h=0时,式中θ等于0,此时折弯机没有动作,机器人也没有动作。当折弯机起动后,h的值发生变化,通过上述推导可以计算出机器人的实际坐标。
例如,如当输入参数如附表时,目标是将工件折成90°,可以计算出当h取不同值时,当前机器人的姿态都会发生变化。
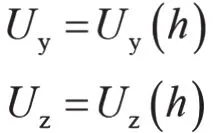
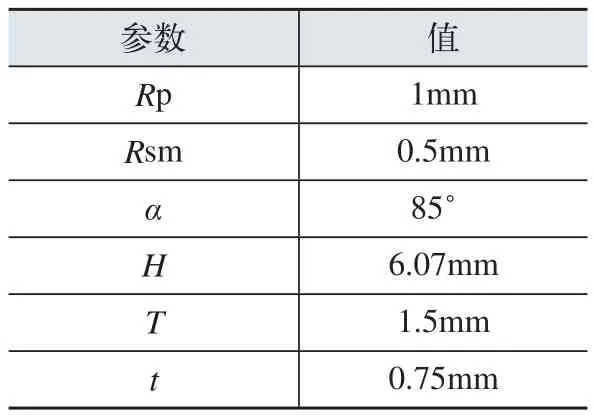
模具及工件参数
如图8所示,折弯机上模向下运动后,机器人的动态点(图8中的U点)的Y坐标会发生少量的偏移,但Z坐标将会向下发生变化,同时回转角W也在逐渐变大,直到45°停止。可以看出Z和W的变化曲线并非完全的直线,也就说明Z和W相对于折弯机动作距离并不是线性关系。
四、试验验证
为验证此套算法应用于钣金折弯上的效果,采用实际机器人来进行折弯。机器人负载165kg,工件尺寸600mm×200mm×1.5mm,折弯角度为90°,其他模具和工件的参数如附表所示。
将计算出来的机器人姿态存入机器人程序中,并使用运动指令来操作机器人。使用PLC来传输折弯机到机器人之间的信号,以保证折弯机和机器人通信的实时性。
如图9所示,机器人带着工件运动至折弯位置,随后折弯机起动。当折弯机上模到达夹紧点后,发送信号给机器人,随后折弯机上模和机器人同时运动,完成整个折弯过程。最后,折弯机回上死点,机器人带着折弯后的工件离开折弯机。图10是90°折弯后的工件。
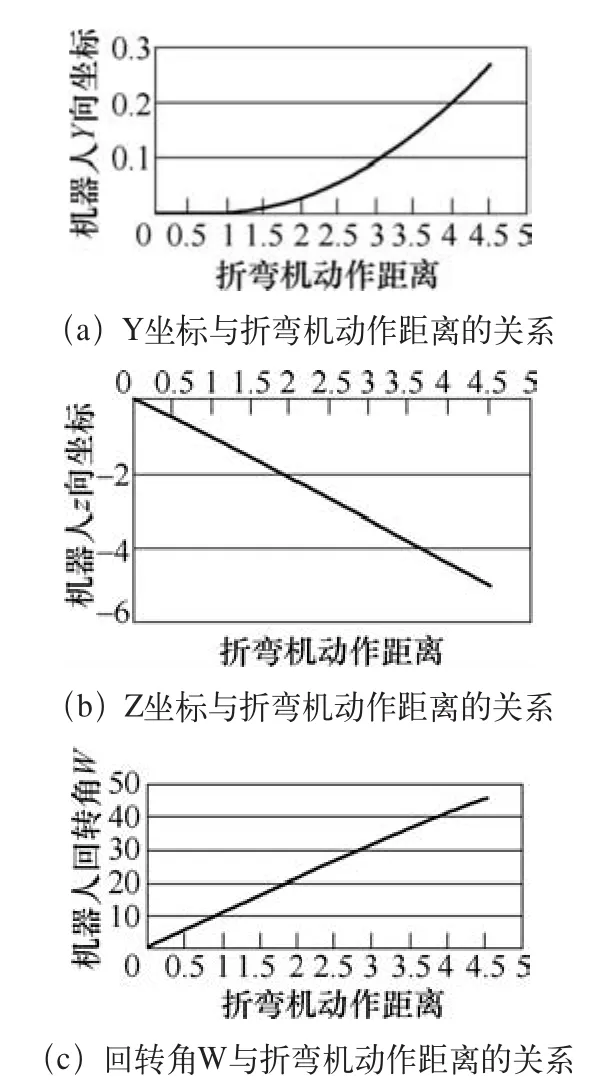
图8 机器人姿态与折弯机动作距离的关系
从图10可以看出,工件未发生变形,这就说明机器人和折弯机的同步效果非常一致。而通过图11可以了解到,一旦折弯机滞后,或机器人滞后,折出来的工件都会发生变形,从而这个工件就会成为次品,影响后续生产。

图9 机器人折弯跟随试验过程

图10 折弯90°的效果

图11 机器人和折弯机的同步和非同步性
五、结语
针对机器人折弯中的跟随问题,分析了折弯工艺,建立了几何模型,并通过模型的计算推导出折弯过程中的机器人姿态,将姿态存入机器人编程语言后,可实现机器人的跟随折弯。最后,通过机器人与折弯机组成的整套系统,对算法进行了验证,结果表明机器人跟随折弯的效果良好,成品工件能够符合工艺需求。
——WILA气动夹具系列

