以学生发展为本

刘梁生

有人曾经说，“教学是一门遗憾的艺术”。教学“圆的面积”这节内容时，我在这门遗憾的艺术中获得了一点点的成功。兴奋之余，我对自己的教学进行了反思。

在以往的教学中，我发现学生对圆的面积公式的理解只是停留在“知其然，而不知其所以然”的层面，不会把所学的知识应用到实际生活中。自己也感到这节内容不容易上活。为此，在教学设计时，我仔细研读教材，依据学情，将教学目标定为：学生理解圆面积公式的推导过程，并能运用公式解答一些简单的实际问题。同时，设计相应的活动，激发学生参与的兴趣，培养学生的动手操作能力和分析、概括能力，发展学生的空间观念。以下是几个主要的教学环节。

一、导入：在观察中引入

多媒体出示奥运五环、鸟巢、运动场等图片。

师：你们有办法求出运动场的面积吗？这节课我们一起学习圆的面积。

教师拿出一个圆形纸片贴在黑板上，提问：我们已经认识了圆，也学习了如何计算圆的周长。已知圆的半径，怎样求圆的周长？已知半径，怎样求圆周长的一半？

师：什么是圆的面积？（就是指这个圆面所占平面的大小）你有什么办法求出圆的面积吗？

结合学生的回答，师生共同投入到新课的学习中。

二、探究：在活动中理解

1.复习旧知

师：以前我们学过哪几种平面图形的面积计算？在学习三角形、平行四边形和梯形的面积公式时，是采用什么方法来推导公式的呢？（课件演示）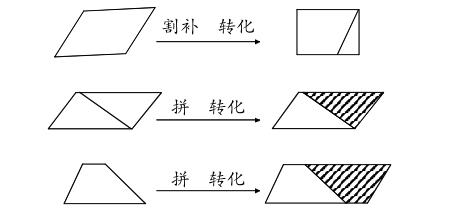

复习时，我先让学生回忆以前学过的平面图形的面积公式的推导方法，并利用多媒体课件直观再现推导过程。学生在回顾旧知识的过程中领悟到这些平面图形面积公式的推导都是通过切、割、拼的方法，把要学的图形转化成已经学过的图形来推导面积公式的。

2.引导学生主动参与知识的形成过程

师：对于圆的面积公式，你们打算怎样进行研究呢？

生：我们可以像前面学习三角形、平行四边形和梯形的面积公式一样，通过切、割、拼的方法，把圆转化成已学过的图形推导它的面积公式。

师：你们有办法把圆形转化为我们已学过的平面图形吗？请你们利用手中的纸片和工具通过小组合作进行研究。小组内先商量好采用的方法，再动手试一试。

学生6人为一个小组进行剪拼，教师巡视。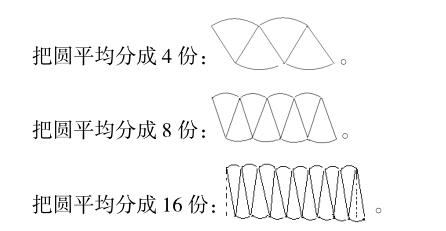

师：通过折一折、剪一剪、拼一拼，你有什么发現？

引导学生比较：把4个等圆分别平均分成4等份、8等份、16等份、32等份后拉开，看曲线的变化，你发现了什么规律？（课件演示曲线接近直线的过程）

教学时，教师作为引导者只是给学生指明了探究的方向，而把探究的过程留给学生。学生则以小组为单位，通过合作剪拼，把圆转化成学过的图形（平行四边形）。教师把各小组剪拼的图形逐一展示后，又结合课件演示，引导学生通过观察发现分的份数越多，拼成的图形就越接近长方形，并从中发现圆和拼成的长方形之间的关系。

3.推导圆的面积公式

教师用课件演示圆剪拼成近似长方形的过程，帮助学生思考。

学生在小组内讨论，然后推导圆面积公式。

讨论提纲：

（1）原圆形面积与剪拼后图形的面积有什么关系？

（2）剪拼后图形的长相当于圆的哪部分？宽相当于圆的什么？

（3）剪拼后图形的面积结果是多少？

各组派代表汇报讨论的结果，学生拿着各自的剪拼图说出推理的过程。教师根据学生的汇报板书如下。

这样由扶到放，由现象到本质进行引导，学生始终参与到把圆转化为长方形的探索活动中。在这一过程中，学生的思维在交流中碰撞，在碰撞中发散，思维的能动性和创造性得到充分激发，分析问题和解决问题的能力得到了提高。

4.巩固知识

（1）例题：一个圆的半径是10厘米，它的面积是多少平方厘米？

（2）思考题：求体育场的面积。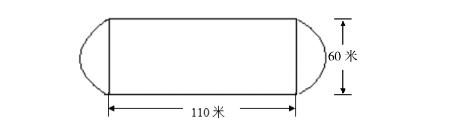

课后思考：如下图，将圆平均分成16等份，拼成近似三角形和近似梯形，怎样推导圆面积公式？

由这节课的教学我认识到，在数学课堂上，要树立以学生发展为本的理念，发挥学生学习的自主性和创造性，让学生在自主探索中不断地发展思维、培养能力。

（作者单位：衡阳市实验小学）