民间金融网络中的风险传染机制与监管策略
张 欣,苏继超
(哈尔滨工业大学 人文社科与法学学院,哈尔滨 150001)
0 引言
在金融抑制背景下,民间金融利用其在信息、抵押机制与交易成本等方面的优势,有效地满足了民营中小企业的融资需求,在弥补正规金融的市场缺位上有重要作用。随着民间金融范围逐渐扩大、形式不断创新,其对整体经济和正规金融的影响日趋深刻。民间金融风险来源复杂,长期累积易形成系统性风险,危及整个经济体系的安全。党的十八大以来,中央多次强调维护金融稳定和防范系统性、区域性金融风险的重要性,特别要防范“灰犀牛事件”和“明斯基时刻”。这对剖析金融体系中风险传染机理,以及风险出现时开展有效干预提出了迫切要求。本文将复杂网络上的传播动力学理论引入民间金融风险的研究中,构建风险传染模型——将小世界网络模型和SEIR传染病模型相结合,引入监管部门干预这一外生因素,使用2014—2016年各省公开的小额贷款公司数据,并进行网络仿真拟合,从而探讨监管部门对民间金融风险的干预策略。
1 民间金融网络风险传染机制建模
1.1 民间金融网络选择与算法构建
由于民间金融网络不存在“大而不倒”金融机构,而且民间金融机构更倾向基于地缘、亲缘开展业务,而在规模扩张后又会出现一定程度的跨区业务扩展,因此,民间金融网络呈现出小世界网络的特征。Watts和Strogtz发现:作为从完全规则网络向完全随机网络的过渡,只要在规则网络中加入一定比例的随机性连边就可以产生具有小世界特征的网络模型,这就是WS小世界网络模型。具体算法构造如下:
(1)从规则图开始:给定一个含有N个节点的环状最近耦合网络,其中每个节点都与它左右相邻的各K 2个节点相连,K是偶数;
(2)随机化重连:以概率 p随机地重新连接网络中原有的每条边,即把每条边的一个端点保持不变,另一个端点改取为网络中随机选择的一个节点。其中规定不得有重边和自环。
在具体算法实现中,可以把网络中所有节点编号为1,2,…,N。对于每一个节点i,顺时针选取与节点i相连的K 2条边中的每一条边,边的一个端点仍然固定为节点i,然后再以概率 p随机选取网络中的任一节点作为该条边的另一端点。小世界网络的度分布也可以用泊松分布来表示,其度分布在均值处有一峰值,并且呈指数衰减。
1.2 民间金融网络风险传染模型的选择与构建
根据前文所述的传染病模型,我们引入模型设计综合性更强、更贴近实际情况的SEIR传染病模型,将民间金融风险传染的过程分为未知状态S、潜伏状态E、感染状态I和免疫状态R,并将监管部门M对民间金融风险的干预能力考虑到模型中。以此分析我国民间金融市场间的风险传染状态,并在此基础上提出相应的金融风险预防和控制策略。
民间金融网络风险传染过程中个体状态转移规则为:
(1)未知状态个体受处于感染状态邻居的影响,以α1的概率受到影响并进入潜伏状态;同时在干预系数α2比例下的部分节点会成为控制节点,变为潜伏状态,其中α1+α2=1;
(2)潜伏状态个体以β1的概率变成感染状态,并在下一时步对其邻居节点造成感染威胁,而潜伏状态中的控制节点会以β2的概率变成免疫状态个体,其中β1+β2=1;
(3)感染状态个体以γ的概率转化为免疫状态,在下一时步保持免疫状态,并对其邻居节点产生示范保护作用。
民间金融SEIR传染病模型具体如图1所示。其中,S表示未知状态的民间金融机构,E表示潜伏状态的民间金融机构,I表示已处于感染状态的民间金融机构,R表示处于免疫状态的民间金融机构,M表示监管机构。
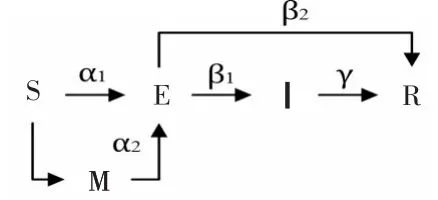
图1 民间金融SEIR风险传染模型
根据SEIR传染病模型,建立在监管部门干预下的民间金融网络风险传染平均场方程:
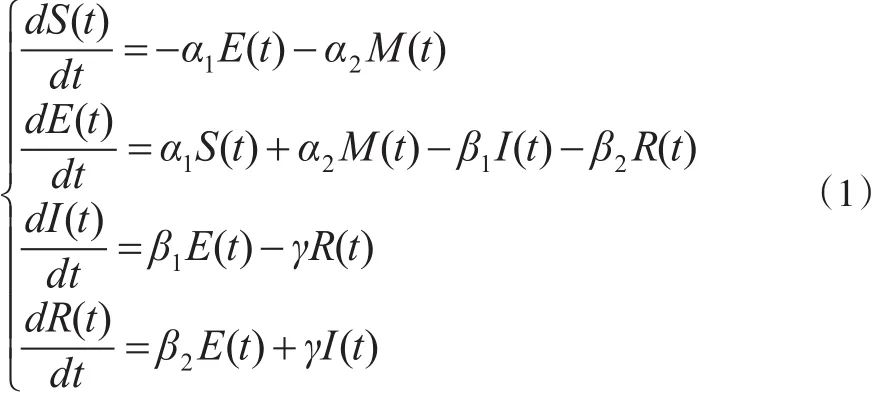
其中,dS(t)/dt、dE(t)/dt、dI(t)/dt和 dR(t)/dt分别表示未知状态、潜伏状态、感染状态和免疫状态的人数所占比例的变化率。上述转化率参数和干预系数的约束具体为
1.3 对状态转移概率β1和γ的实现模型
在金融风险传染的过程中,未知状态S会全部转化成潜伏状态E;但是,在干预系数α2的影响下,有一部分节点被标记为控制节点,并从潜伏状态E按照干预系数β2直接转化为免疫状态R;其余节点则会根据周围邻居节点的状态情况按照概率β1从潜伏状态E转化成感染状态I,而感染状态I则会按照概率γ转化为免疫状态R。β1和γ的转化概率模型具体如下:

其中,节点i为网络中任意一个节点,而节点 j表示节点i的邻居节点,kj表示节点 j的度占整个民间金融网络节点数量N的比例,kj∈[0,1]。若kj越大,说明与节点j相联系的民间金融机构数量越多,节点 j在民间金融网络的业务量和资金流动量的比重也相应越大,对节点i的影响程度也越大。而λj则是调节因子,当节点 j为潜伏状态时不产生外部性;当节点 j为感染状态时会对整个系统产生负外部性,使得周围节点有更大概率进入感染状态;当节点 j为免疫状态时会对整个系统产生正外部性,使得周围节点有更大概率进入免疫状态,因此根据节点 j的不同状态对其赋予不同的调节因子。假定节点i状态的变化完全取决于其邻居节点的影响,结合上一时步t-1处于感染状态(或免疫状态)的邻居节点占全部邻居节点影响力的比例,即可得出节点i在当前时步t中转变其状态的概率。
2 仿真结果与分析
基于前文的模型分析,接下来将从我国各省民间金融的有关统计数据中提取有用信息,构造区域性民间金融网络,并在此基础上根据SEIR传染病模型,对参数比较和监管干预策略进行数值仿真,各省小贷机构数量如表1所示。
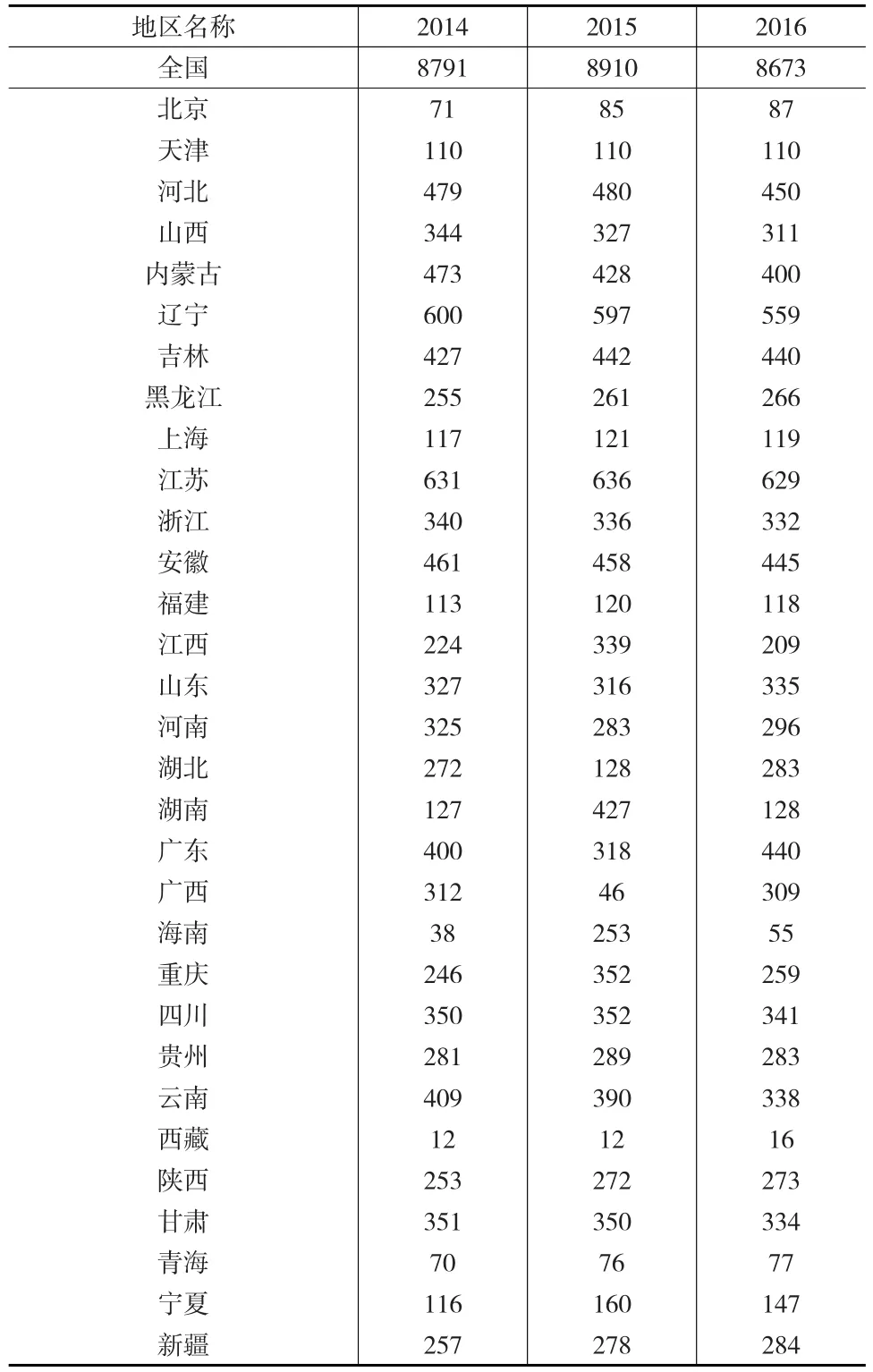
表1 2014—2016年全国各省小额贷款机构数量统计
结合中国人民银行2014—2016年对我国各省小额贷款公司的机构数量等数据的统计分析结果不难发现:经济总量较大地区的小额贷款公司数目都在300家左右,部分经济发达地区如江苏省、广东省、浙江省和山东省的小额贷款公司规模甚至超过300家。结合上述数据分析结果,本文设定区域性民间金融网络的规模大小为N=300,并通过重复实验的方式来减少随机均匀分布参数的不确定性影响。
表2给出了生成的网络基本参数,从中可以看出该网络具有较大的聚类特性,又具有较短的平均路径长度,符合小世界网络的特征要求。

表2 生成小世界网络后的基本参数
小世界网络的生成示意图和节点度的概率分布图具体如图2和图3所示。

图2小世界网络生成示意图
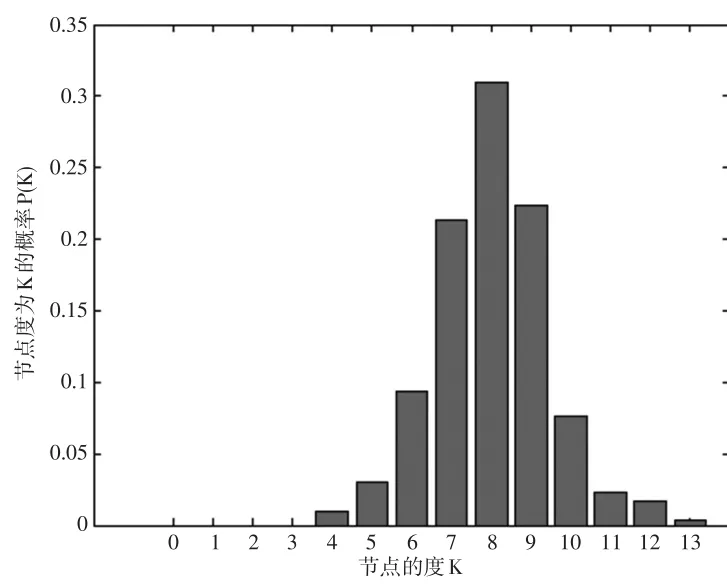
图3 小世界网络节点度的概率分布图
本文对所有仿真对比实验都进行20次重复迭代实验,并取所得数据的平均值作为最终实验结果。利用Matlab软件进行编程,并完成对比仿真实验的有关参数设置和仿真图像绘制。
仿真实验的设计主要从四个方面进行研究:一是从有无监管部门干预的角度考察民间金融风险传染影响;二是从不同干预强度的角度来考察民间金融风险传染影响;三是从不同免疫策略的角度来考察风险传染影响;四是从监管滞后的角度考虑民间金融的风险传染影响。
2.1 有无监管部门干预情况下的风险传染影响
实验利用Matlab随机选择网络中1%的节点作为金融风险爆发点,具体节点编号为(13,118,237)。假定在监管部门干预的情况下,网络的干预系数 β2为1%,即利用Matlab随机选择三个控制节点,具体节点编号为(24,123,263);在无监管部门干预的情况下,网络中没有控制节点,SEIR模型在不受监管部门影响的情况下按照SEIR传染机制进行风险传染行为。本文选取这两种实验条件下的I态和R态密度进行比较。仿真实验图像如下页图4所示。
从I态密度的变化上看,在无监管部门干预风险传染过程的实验条件下,I态密度的峰值为0.96,且持续的时间更长,传染范围更广,整个民间金融网络在25个时步后才将所有I态转化成R态节点;在有控制节点的实验条件下,I态密度的峰值为0.81,比前者低15.6%,网络在20个时步内就将所有I态节点转化为R态,比前者少了20%。
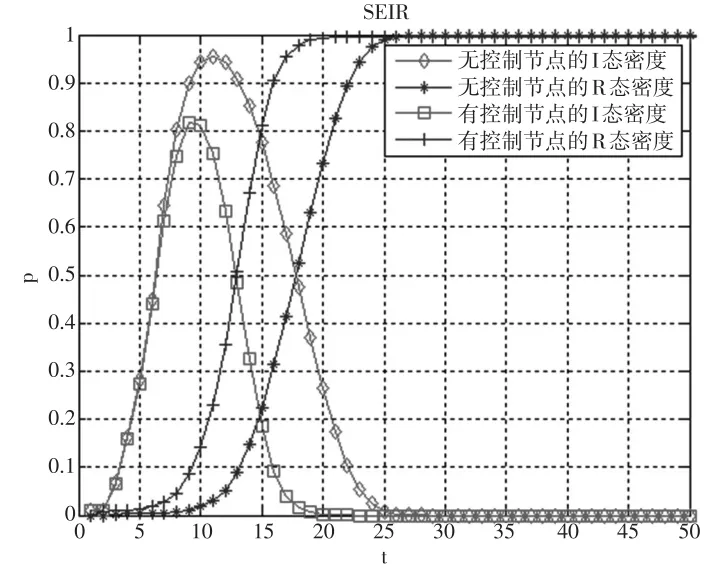
图4 有无控制节点的I态和R态密度
从R态密度的变化上看,有控制节点网络的R态在速度和效率上要远高于无控制节点的实验网络。有控制节点网络在20个时步后达到稳态收敛,而无控制节点网络在25个时步后才能达到稳态收敛。
2.2 不同政府监管强度情况下的风险传染影响
相比于弱监管强度条件,强政府监管条件下的网络控制节点占整个网络节点的比例更大。实验假设在弱监管条件下,网络的干预系数β2为1%;而在强监管条件下,网络的干预系数β2为2%。根据网络规模大小,在弱监管条件下所选择的控制节点编号为(24,123,263),而强监管条件下的控制节点编号为(24,59,109,178,233,264)。同样选取了这两种不同实验条件下的I态和R态密度进行对比。仿真实验图像如图5所示。

图5 不同监管强度下的I态和R态密度
从I态密度的变化看,监管部门的监管强度越大,I态的峰值越低,当网络中的干预系数是2%的情况下,I态密度的峰值为0.7;当网络中的干预系数为1%时,I态密度的峰值为0.82,比强监管条件下高出17.1%。说明随着监管部门干预力度的增大,对民间金融网络的风险传染抑制能力也越强。从R态密度的变化上看,在强监管情况下,网络中R态密度的收敛速度要快于弱监管情况。
2.3 不同免疫策略情况下的风险传染影响
在复杂网络的研究中,如何选择合适的免疫策略对传染病防控有着非常重要的意义。目前主流的免疫策略有三种:随机免疫、目标免疫和熟人免疫。结合民间金融网络风险传染的实际情况,本文在实验中设置了三种针对风险传染的免疫策略:随机性免疫策略、规则性免疫策略和针对性免疫策略。下面对三种策略进行说明:随机性免疫策略是指监管部门在非正规金融网络中随机选择控制节点的策略形式;规则性免疫策略是指监管部门按照一定的间隔距离选择控制节点的策略形式;针对性免疫策略是指监管部门根据调查评估结果所确定的高风险机构作为控制节点的策略形式。
实验中随机选择网络中1%的节点作为金融风险传染爆发点,具体节点编号为(13,118,237)。考虑到控制节点数量对实验结果的影响,为了保证不同免疫策略之间的可比较性,本文设定所有策略的控制节点数量一致,都占据网络节点总量的2%。在随机性免疫策略条件下,随机在网络中选择控制节点,具体节点编号为(264,159,109,233,24,178);在规则性免疫策略条件下,按照监管距离为50的标准,在网络中选择控制节点,具体节点编号为(50,100,150,200,250,300);在针对性免疫策略条件下,选择距离风险爆发点最近的向上向下取整点作为控制节点,具体节点编号为(10,20,110,120,230,240)。选取这三种策略所出现的I态密度进行对比实验。实验仿真图像如图6所示。
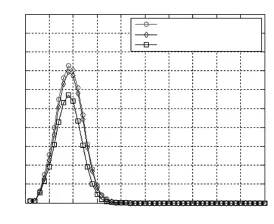
图6 不同免疫策略下I态密度
从图6中可以发现,针对性策略控制的效果优于规则性策略,而规则性策略的效果又要优于随机性策略,即:针对性策略效果>规则性策略效果>随机性策略效果。其中,针对性策略的I态密度峰值为0.57,规则性策略的I态密度峰值为0.69,随机性策略的I态密度峰值为0.72。因此,规则性策略效果虽然优于随机性策略效果,但是二者之间的差距较小;而针对性策略效果要远比其他两种策略的效果好,感染峰值比规则性策略低17.4%,比随机性免疫策略低20.8%。
2.4 不同监管滞后情况下的风险传染影响
由于监管部门与民间金融网络之间存在信息不对称情况,因此监管部门想在第一时间对民间金融网络中的风险进行控制是存在困难的。在现实情况中,监管部门一般采取定期搜集民间金融机构信息数据的方法来减缓这种信息不对称问题。考虑到监管部门介入的滞后性问题,控制节点对风险控制的时机易出现迟滞问题,导致更大的风险传染范围和传染影响。
实验随机选择网络中1%的节点作为金融风险起始点,具体节点编号为(13,118,237)。为了保证不同滞后时步下的I态密度的可比较性,本文以规则性控制策略为基础,设定所有控制节点数量一致,都是网络节点总量的2%,控制节点的具体编号为(50,100,150,200,250,300)。假定如果调查信息搜集间隔为n个时步,那么滞后时步也为n。仿真程序分别在无滞后时步条件,滞后5个时步、10个时步、15个时步、20个时步、25个时步和30个时步的条件下进行实验,选取不同滞后时步的I态密度收敛时间进行比较。仿真实验图像如图7所示。
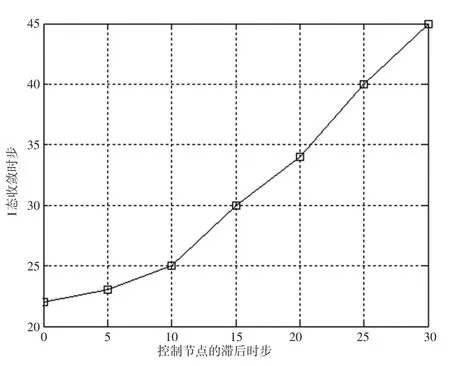
图7控制节点在不同滞后时步下的I态收敛情况
从图7中可以发现,监管滞后的时间越长,I态密度的收敛时步就越长,二者之间存在正相关关系。不同信息搜集频率导致的监管滞后效果也有很大差异。在监管滞后10个时步以内,感染态的收敛时步增长速度较低;而在滞后10个时步以上时,感染态的收敛时步增长速度很快,说明滞后10个时步以后对民间金融网络的冲击变得更大。因此,可以认为存在一个信息搜集时间间隔的阈值:在阈值以下,监管滞后带来的影响较小;在阈值之上,监管滞后带来的影响较大。
3 结论
本文在民间金融风险传染研究中引入复杂网络中的传播动力学理论,以小世界网络上的SEIR传染病模型为基础,首先刻画了复杂民间金融网络的风险传染过程,厘清风险传染机理;然后,利用中国人民银行公布的2014—2016年小额贷款公司数据,构造出区域性小世界民间网络,建立监管部门干预下的民间金融风险传染模型;最后,从监管强度、监管策略和滞后监管三个角度设计仿真实验,通过数值仿真对风险传染和监管干预策略进行研究。
通过理论分析和数值仿真,可以得到如下结论:
(1)民间金融网络具有明显的小世界网络特征,民间金融风险在这样的网络中一旦爆发,极易累积风险,出现大范围的风险传染问题。
(2)民间金融网络在风险爆发时,有无监管部门采取措施进行干预对风险传染的影响有很大差异,尤其体现在风险扩散峰值和扩散范围两个方面。无干预情况下的风险传染比有干预情况要有更高的峰值和更大的扩散范围。因此,有关部门应该采取主动策略进行干预,不可放任风险扩散。
(3)当风险传染源一致,监管部门介入强度较高时,风险扩散峰值要低于介入强度较低的情况。因此,在客观条件允许的情况下,监管部门应该采取更为强力的监管措施。
(4)不同免疫策略会出现不同的干预效果。在本文提出的三种免疫策略中,假定风险传染源头一致,则针对性免疫策略的效果要明显优于随机性免疫策略和规则性免疫策略,这可以使干预成本不变的情况下得到更好的风险控制效果。因此,监管部门在风险爆发前应做好区域内民间金融机构的摸底调查工作,对易出现风险的机构进行提前判断,尽量能够在距离风险爆发点最近地方设置控制节点,这样才能使针对性免疫策略得以更好实现。
(5)监管滞后问题源于民间金融机构与监管部门之间存在的信息不对称问题。在滞后10个时步以内时,感染状态的节点都可以在25个时步内得以收敛;但是一旦滞后时步在10以上时,收敛的时间出现了大幅增加,说明监管滞后带来的影响较大。因此,监管部门应该努力减轻监管滞后给民间金融风险感染带来的影响,防止某些民间金融机构打着“普惠金融”旗号危害金融系统安全。
民间金融风险传染的网络理论是一个综合金融学、网络理论和系统动力学的交叉领域。本文仅是对其研究的初步探索,未来可以在如下两方面再做推进:一方面,研究民间金融网络的信息不确定性问题对风险传染的推动作用;另一方面,利用SIRS传染病模型考虑某一民间金融风险所带来的其他衍生风险对民间金融网络结构的影响以及对正规金融和实体经济的冲击。

