湖北省最低工资就业效应研究

刘玉成

（长江大学a.经济学院；b.长江经济带研究院，湖北 荆州 434023）

0 引言

最低工资制度的诞生已有100多年的历史，目前已成为世界各国的基本社会保障制度之一。在就业领域内，最低工资的影响历来受到各国研究者的重视，近年的研究有向微观层面延伸的趋势，在最低工资对不同性别、年龄、肤色、收入层次、劳动技能结构等劳动者的就业影响方面产生了较多研究成果。但是，由于研究方法、研究工具、研究对象、研究数据等方面的差异，导致研究结论并不能趋于一致。Katz、Card、Neumark等著名学者之间就曾经爆发过激烈的学术争论[1-4]，Teulings甚至把最低工资对就业的影响称之为“最低工资悖论”[5]。目前的主流观点认为最低工资对就业具有负面影响，且对低收入劳动者、低技能劳动者、女性等群体负面影响更显著[6-9]。

我国实行最低工资制度仅有20多年，随着近年来各地最低工资标准频繁上调，最低工资对就业的影响日益显现。在最低工资的就业影响效应方面，研究者对农民工就业[10]、不同行业就业[11]、不同部门就业[12，13]、不同类型劳动者就业[14,15]作了较多关注。从现有文献来看，研究主要集中在宏观层面，且大多使用截面数据和参数模型。本文在前期利用宏观数据研究[16,17]的基础上，进一步基于湖北省地级市的数据从更为微观的角度来考察最低工资对就业的影响。基于最低工资对就业影响的复杂性，本文假设最低工资与就业之间的函数关系未知，由此利用半参数模型来探索最低工资的就业影响效应。

1 理论模型及估计方法

对于面板参数模型来说，需要假定变量之间的关系为已知并用确定的数学模型来模拟，但经济变量之间的关系非常复杂，而且会受到各种影响因素的干扰，因此参数模型虽然可以简化变量之间复杂的关系，但同时也可能导致估计偏差。而非参数模型不需要设定变量之间的函数关系，且在模型的假设条件方面更为放松，由于非参数模型的诸多优点，近年来越来越多的研究者采用非参数模型来研究变量之间的关系。

为了研究变量Y与 X1，X2，…，Xk之间的关系，可以建立下列非参数面板模型：

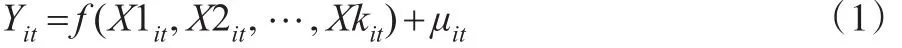
其中，f为未知光滑函数，i=1，2，…，N 表示个体，t=1，2，…，T 表示时间，μit为随机误差项，且满足条件E(μit|X1it，X2it，…，Xkit)=0，Var(μit|X1it，X2it，…，Xkit)= σ2，σ为常数。

对模型（1）来说，当k值较大时将导致模型中的回归元较多，由此非参数回归估计量的有效性和收敛速度在很大程度上受到变量维数(k×N×T)的制约。实际中通常对模型（1）进行改进，即在模型的非参数部分只保留部分变量，由此形成半参数面板模型:

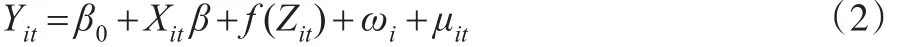
其中,β为m×1维系数列向量，X为1×m维变量行向量，Z为k-m维变量行向量，X和Z中的变量都来自X1，X2，…，Xk 。不失一般性，假设 X=(X1，X2，…，Xp)，Z=(X(p+1)，X(p+2)，…Xk)。 ωi为未知的个体特征差异，ωi、μit构成模型的误差项。

当模型（2）中的个体特征差异ωi具有固定效应时，可以使用一阶差分来处理：

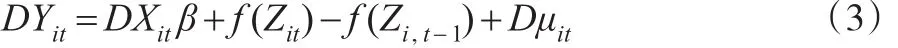
其中,DYit=Yit-Yi，t-1，DXit=Xit-Xi，t-1，Dμit=μitμi，t-1，D为差分算子。对模型的非参数部分 f(Zit)-f(Zi，t-1)可以采用非参数光滑法进行拟合，目前常用的非参数光滑方法包括核函数光滑、样条光滑和多项式光滑等，本文将采用核函数光滑法、利用局部加权多项式拟合以最优化均方根误差

2 实证分析

2.1 研究变量及数据统计描述

实证采用了湖北省13个地级市的面板数据，时间范围为2000—2014年，因变量为就业，观察变量为最低工资。此外，本文还在模型中引入了较多控制变量，这些控制变量的选择来源于就业相关研究文献。变量数据来源于各年度《湖北统计年鉴》《地方统计年鉴》《城市统计年鉴》，部分数据来源于调研资料。表1列出了变量含义及统计描述。

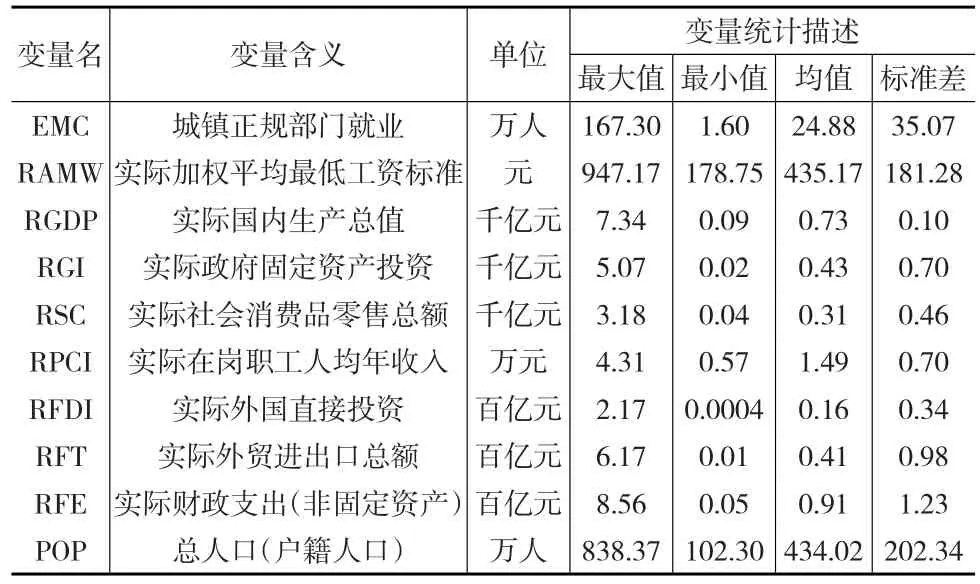
表1 变量含义及统计描述

本文的控制变量所涉及的影响因素主要来自于四个方面：（1）经济发展水平，用GDP、社会消费品零售总额和职工收入来度量；（2）投资水平，用固定资产投资和财政支出来度量；（3）劳动供给水平，用人口来度量；（4）经济开放水平，用FDI和外贸进出口总额来度量。已有研究表明，这些因素均会对就业产生影响。本文引入这些控制变量，一方面希望在控制这些变量的基础上更准确地识别最低工资的影响效应，另一方面希望尽量保证最低工资变量的外生性，从而最大限度克服内生性问题。

2.2 模型构建及估计

根据前文理论模型分析，本文以实际最低工资变量RAMW和滞后的实际最低工资变量RAMW(-1)为模型的非参数部分，分别建立如下的两个局部线性半参数面板模型：

模型（4）为主要观察模型，为了与模型（4）进行对比，本文也给出了参数面板模型：

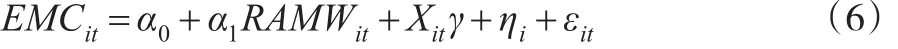
模型（4）至模型（6）中，i=1，2，…，13表示地区数，t=2000，2001，…，2014 表示时间，β、β′、γ为系数列向量，ω、ω′、η为地区特征差异，μ、μ′、ε为随机误差项，f、g为未知的平滑函数，X为变量行向量，且X的表达式为X=(RGDP，RGI，RSC，RPCI，RFDI，RFT，RFE，POP)。

对模型（4）、模型（5）采用核函数光滑法进行拟合，选择Epanechnikov核密度函数为其中I(|u|)为指标函数，且 I(|u|≤1)=1，I(|u|＞1)=0。利用交错鉴定法确定窗宽为110.25，经过反复模拟确定加权多项式的最高次数为4。模型（6）经Hausman检验和冗余固定效应F检验，确定为固定效应估计类型。

2.3 实证结果及分析

模型（4）到模型（6）线性部分的参数估计结果见表2，残差走势见下页图1。

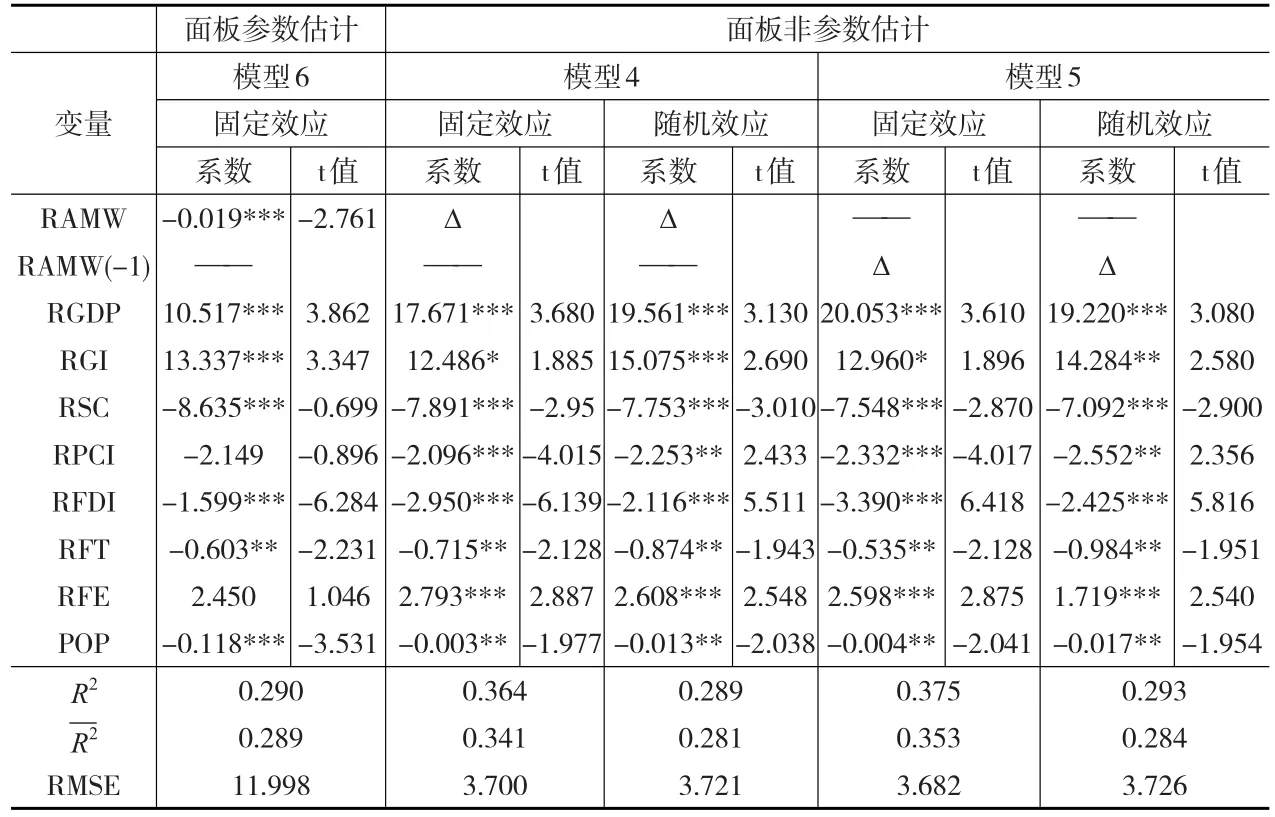
表2 模型估计结果

比较图1a和图1b可知，参数面板估计的残差波动幅度较大；从表2可知，参数面板估计的均方根误差RMSE显著大于半参数面板估计。由此可以佐证，半参数面板估计比参数面板估计更优。同时，从表2的线性部分估计可知，各变量的系数符号一致，显著性变化不大，表明模型和控制变量具有稳定性。

对于模型（4）和（5），通常可以采用固定效应估计或随机效应估计，但目前缺乏有效的手段对两种估计方法进行取舍，本文通过对残差进行比较来确定估计方法。观察图1b可知，固定效应估计的残差走势比随机效应估计更为平稳、波动幅度更小，从表2可知模型4固定效应估计的均方根误差（RMSE=3.700）小于随机效应估计的均方根误差（RMSE=3.721），模型5固定效应估计的均方根误差（RMSE=3.682）小于随机效应估计的均方根误差（RMSE=3.726）。由此可知，对于模型（4）采用固定效应估计更优。对于模型（5），类似的分析可知采用固定效应估计更优。

图1参数估计与半参数估计残差走势对比

模型（4）、模型（5）的非参数部分拟合如图2，图2中阴影部分给出了最低工资（滞后的最低工资）就业影响效应的95%置信区间，横轴为实际最低工资（滞后的实际最低工资），纵轴为中心化的就业边际影响效应。图中的拟合曲线表达出最低工资（滞后的最低工资）对就业影响的复杂关系，且二者之间呈现出非线性关系。

通过对图2的分析可知：（1）关于最低工资的当期影响。最低工资对就业的影响最初表现为正向影响，但随着最低工资逐步提高该正向影响逐步缩小，在最低工资超过一定的标准时（约为500元），最低工资对就业的影响由正向转向为负向，且随着最低工资标准的继续提高负向影响逐步扩大；当最低工资标准较高时（拐点约为850元），最低工资的负向影响达到最大，当最低工资继续增加时，最低工资对就业逐渐表现出正向影响。（2）关于最低工资的滞后影响。最初的滞后影响为负向，当最低工资标准逐步提高时，负向影响逐步缩小，当最低工资超过一定标准时（约300元），最低工资对就业表现出正向并在一定区间内（约300～700元）维持小幅波动，当最低工资继续增加时，滞后影响表现出负向，在最低工资约850元时，负向影响达到最大，此后随着最低工资增加而转向为正向影响。（3）结合最低工资的当期影响和滞后影响来看，最低工资对就业的影响存在自我修正机制。当最低工资标准较低时，最低工资的当期影响和滞后影响的方向相反，滞后影响在一定程度上修正了当期影响，虽然在时间上并不完全同步，但也反映出最低工资对就业的影响存在自我修正机制。总体来看，这种修正作用比较缓慢且幅度有限，因此在实际中需要用“政策+经济系统自身调节”的方式来舒缓最低工资对就业的冲击效应。另外也应该看到，当最低工资标准较高时（实际最低工资超过850元），最低工资对就业的当期影响和滞后影响是同向的，此时自我修正机制并未发生作用。

图2实际最低工资的就业影响效应

3 结论

本文基于湖北省地级市2000—2014年的面板数据，利用半参数面板模型研究了最低工资对就业的影响效应，得出主要结论如下：

（1）在利用模型研究最低工资对就业的影响时，发现半参数面板模型要优于线性面板模型，而固定效应半参数模型要优于随机效应半参数模型，而且最低工资对就业影响的半参数面板模型具有较好的稳定性。

（2）最低工资与就业之间表现出非线性关系。在现有文献中，通常假定最低工资与就业之间的关系为线性，由此利用多元线性模型来研究二者之间的关系，而本文利用线性模型和半参数模型进行对比研究，发现二者之间表现出复杂的非线性关系，也不能用简单的“U”型关系来描述。

（3）最低工资对就业的影响具有阶段性特征。最低工资对就业存在显著的当期影响和滞后影响，但是在最低工资标准较低阶段和较高阶段，最低工资对就业的影响效应并不相同，这种阶段性特征在最低工资的当期影响和滞后影响中都得到体现。在最低工资较低阶段，最低工资对就业的当期影响主要表现为正向影响，滞后影响主要表现为负向影响；在最低工资较高阶段，最低工资对就业的当期影响和滞后影响均表现出正向影响；在最低工资由较低阶段向较高阶段转变的过程中，最低工资对就业的当期影响以负向为主，而滞后影响以正向为主。

（4）在最低工资上涨过程中，最低工资对就业的影响存在自我修正机制。在实际最低工资低于一定的标准（约850元）时，最低工资对就业的当期影响和滞后影响方向是相反的，这表明最低工资对就业的影响存在一定程度的自我修正机制，使得最低工资对就业的影响不会过度远离均衡。但是当实际最低工资超过一定的标准（约850元）时，这种自我修正机制并不存在。