时间尺度对农田灌溉设计保证率的影响

宰松梅，冯雪芳，仵 峰※，李陆生

（1. 华北水利水电大学水利学院，郑州 450046；2. 河南省节水农业重点实验室，郑州 450046）

0 引 言

随着灌溉水资源供需矛盾的加剧，农业节水备受关注。降水的时空分布不均极大地影响着农业节水工作，康绍忠等[1-2]提出应该加强对农田尺度水分高效利用方面的研究。针对农业节水灌溉的尺度问题国内外进行了一系列的研究，“灌溉水文学”这一概念随之产生[3-4]。目前，在空间尺度效应研究方面已取得了很多有用的成果[5-9]。在时间尺度效应方面的研究，大部分从作物蒸散发角度进行[10-13]，或选用小尺度（日、小时、分钟）分布式水文模型进行流域水文模拟[14]，或采用旬降雨尺度结合降雨中短期预报制定灌溉制度[15]，对于时间尺度效应与灌溉设计保证率之间的关系研究较少。

灌溉设计保证率是灌溉设计工作的基础，是反映灌区效益的一个重要技术指标。灌溉设计保证率的选定，将影响着整个灌区灌溉工程建筑物的规模和灌溉面积的大小，取值太高或太低都是不经济的[16]。目前，根据中国《灌溉与排水工程设计规范》（GB 50288—99）[17]（以下简称“规范”）规定，灌溉设计保证率可根据不同地区、不同灌水方法及不同种植作物种类查表选择，极大地方便了灌溉工程设计工作。随着农业水资源紧缺状况的加剧，对灌溉设计保证率的要求越来越精确。

传统的灌溉设计保证率通常采用典型年法来确定，典型年的选择通常仅考虑降水的数量，并没有考虑降水的时间分布不均问题，而灌溉制度的制订需要精确到月或旬，甚至是周、日。尹正杰等[18]指出，现行的灌溉保证率按年进行评价，而作物的灌溉是按月或旬来管理，二者在时间步长上不同步。针对于此，周潮生等[19]将季调节与连晴天数结合起来计算灌溉设计保证率，以此弥补灌溉设计保证率选定时降雨在时间上的分布不均问题。蔡甲冰等[20]为了消除降雨的时空分布不均问题，提出用作物静灌溉需水量进行频率计算选定设计典型年。罗高荣[21]在考虑实际上游来水、天然降水及作物需水量的随机性的前提下，提出 1种计算灌溉设计保证率的数学模型，以此来提高灌溉设计保证率的保证程度。邹谷泉等[22]采用水利经济分析方法选定灌溉设计保证率。

在审查和参与全国各地小型农田水利工程的过程中，发现传统的典型年法确定灌溉设计保证率在时间尺度上与小型农田水利工程实际存在较大偏差，需要审视现行灌溉设计保证率及其选取方法。本文针对季风气候区夏季降水多、冬季降水少的季节分布不均匀特征[23-24]，以河南省郑州市为例，研究不同时间尺度对灌溉设计保证率的影响，并将不同时间尺度下的降雨量进行对比分析，通过不同时间尺度下的节水效果探讨合适的时间尺度，以期完善灌溉设计保证率的选定方法，推动中国节水灌溉事业的发展。

1 材料与方法

1.1 数据来源

以河南省郑州市为例，郑州市气象基准站站号为57083，位于东经 113.65°，北纬 34.72°，海拔高度为110.4 m。气象数据来自中国气象数据网，取1951—2015年的逐日数据。

按研究目的，将气象数据分为降雨数据和用于修正彭曼公式计算ET0的数据2大部分，该公式所需的主要逐日气象资料包括平均气温、水气压、日照时数、2 m高处风速等。

式中ET0为参考作物需水量，mm/d；Rn为输入冠层静辐射量，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；T为 2 m高处日平均温度，℃；u2为2 m高处风速，m/s；es为饱和水汽压，kPa；ea为实际水汽压，kPa；D为饱和水汽压与温度关系曲线在某处的斜率，kPa/℃；γ为干湿温度计常数，kPa/℃：式中各变量的计算方法具体参考文献[25]。

1.2 灌溉设计保证率

灌溉设计保证率是指灌区用水量在多年期间能够得到充分满足的几率，一般以正常供水的年数或供水不破坏的年数占总年数的百分数表示[25]，利用经验频率公式计算

式中P为灌溉设计保证率，%；m为按设计灌溉用水量供水的年数，a；n为总年数，a。

灌溉设计保证率是灌溉工程参数之一，是规划设计的一个基础指标，其所定数值合理与否将直接影响到工程的规模及效益。

1.3 典型年选择方法

对一个给定灌区，由于降雨量的年际变化，在进行灌溉工程规划时，需要确定一个特定的水文年份，作为规划设计依据，根据设计典型年的气象资料来计算“设计灌溉制度”。

常规典型年的选择采用配线法，其时间尺度为年尺度。该方法从以往的年份中，通过对年尺度下的降雨资料系列排频计算，得到 1条皮尔逊Ⅲ型理论频率曲线，从该曲线上选出2～3个符合灌溉设计保证率的年份，按“年内分配最不利”原则确定典型年，并以此作为拟定灌溉制度的依据。

研究中，首先以年降雨为计算尺度选择典型年，再对相同保证率下不同年份的月、旬降雨进行比较分析。然后以作物需水关键期对应的月、旬的降雨为计算时间段，选出相应保证率时的典型年，并分析其降雨变化。

按照上述拟定的计算时间尺度，运用水文频率计算中的配线法，对郑州市1951—2015年的年降雨量、月降雨量及旬降雨量分别进行排频计算。

1.4 灌溉制度

河南是国家粮食主产区，以冬小麦-夏玉米连作为主，根据多年来的生产经验，4月是冬小麦灌浆期，7月、8月分别为玉米拔节和灌浆期，是以上 2大农作物的关键生育时期[26]。为简化分析，在典型月及典型旬的选择时，重点考虑作物需水关键期，即选择4月、7月和8月进行分析。

在制订作物灌溉制度时，按降雨的年尺度进行排频，选择不同保证率时对应的降水资料，按1.3所述的方法，分别计算不同降雨计算时间段（季尺度、月尺度、旬尺度、日尺度）对应的降雨量，作为农田水量平衡分析中的降雨量，有效降雨参考文献[25]的方法进行计算。

作物需水量计算时，以河南省节水农业重点实验室的试验地为例，其土壤最大含水率为 35%，最小含水率为 16%（均为体积含水率），因当地的地下水埋深超过8 m，地下水补给量暂不计。作物系数查文献[26]得到。冬小麦和夏玉米各生育期内计划湿润层深度如表1所示。

表1 作物各生育期计划湿润层深度及作物系数Table 1 Planned wetted soil depth and crop coefficient in different growth periods

参考作物需水量采用修正彭曼公式，利用EXCEL自编计算程序进行计算，按水量平衡法进行作物灌溉制度的推求。

2 结果与分析

2.1 时间尺度降雨量分析

用皮尔逊Ⅲ型曲线对郑州地区1951—2015年的年降雨数据进行拟合，选出在对应不同灌溉设计保证率下（P=25%、50%、75%、90%）的各典型年，结果如下。

2.1.1 年尺度降雨量

1）典型年降雨量计算

对1951—2015年的年降雨量进行排频计算，当降雨频率与灌溉设计保证率差值在±5%以内，即可选定为典型年。选出的典型年及其降雨量见表2。从表2可以看出，相同灌溉设计保证率下各典型年的年降雨量数值相差较小。

2）典型年的月降水分布

以灌溉设计保证率为 25%为例，在年降雨量相差不大的情况下，将对应的月降雨量进行对比，结果如图 1所示。

从图 1可以看出，在相同灌溉设计保证率下，虽然各典型年的降雨量相差较小，但各典型年对应的月降雨量数值相差较大。如5月份的降雨量最大值是1985年的227.4 mm，最小值是1994年的42.4 mm，相差5倍以上；而8月份的降雨量最大值为2009年的270.2 mm，最小值为1994年的54.2 mm，相差接近5倍，说明灌溉设计保证率按年尺度来选择时，对降雨的时间分布不均问题考虑不足，作物不能很好地利用降雨资源，甚至一部分降雨是无效的，从而造成水资源的浪费。

3）典型年的旬降水分布

对比灌溉设计保证率为 25%时各典型年下对应的 4月、7月、8月的上中下各旬的降雨量，4月上旬降雨量的最大值和最小值分别为1963年的17.8 mm、2009年的0 mm；4月中旬降雨量的最大值和最小值分别为1994年的82.6 mm、2005年的0 mm；4月下旬降雨量的最大值和最小值分别为1963年的5.0 mm、1994年的0 mm和2005年的0 mm。相同频率下各典型年的旬降雨量差值较大，极值分布年份也不同。7月、8月的旬降雨量极差规律与4月相似。

表2 灌溉设计保证率下典型年的年降雨量Table 2 Annual rainfall of typical year under probability of irrigation water requirement

对于作物而言，生长期通常在1 a以内，而且其关键生长期需要精确到月或旬，故在灌溉系统中按年尺度来选定灌溉设计保证率，对于作物而言并不具有代表性，其保证程度也较低。另外，规范[17]中选择典型年按“年内分配最不利”原则，若恰巧选择的典型年在作物生育期内降水较少，为满足作物生长的需要，依靠灌溉系统向作物供水量就多。这样带来的负面影响有 2个方面，一是不利于作物生长期中对降水的充分利用；二是造成灌溉设计工程投资大，与当地生产实际需要脱节。

2.1.2 月尺度降雨量

分别对1951—2015年4月、7月、8月的月降雨量进行排频计算，仍按频率上下浮动5%选出月尺度对应的典型年。灌溉设计保证率相同，根据不同时间尺度选择的典型年年份不同。对比不同时间尺度下4月、7月、8月的降雨量极差，如图2所示。

在灌溉设计保证率分别为25%、50%、75%和90%时，4月、7月和8月的降雨量极差，年尺度大于月尺度（除P=75%的情况，此时由于典型年只有1 a，故年尺度下4月、7月、8月的极差为0），这表明按年尺度选择典型年，其月降雨量值极差大于相应月尺度下的降雨量极差，则降雨量的不均匀程度最高。由于灌溉工程预先根据典型年确定相应的灌溉规模及灌溉量，在灌溉量一定的情况下，作物需水能否得到满足就取决于降雨的保证程度，故典型年选择的时间尺度合理与否将影响到灌溉设计保证率的保证程度。

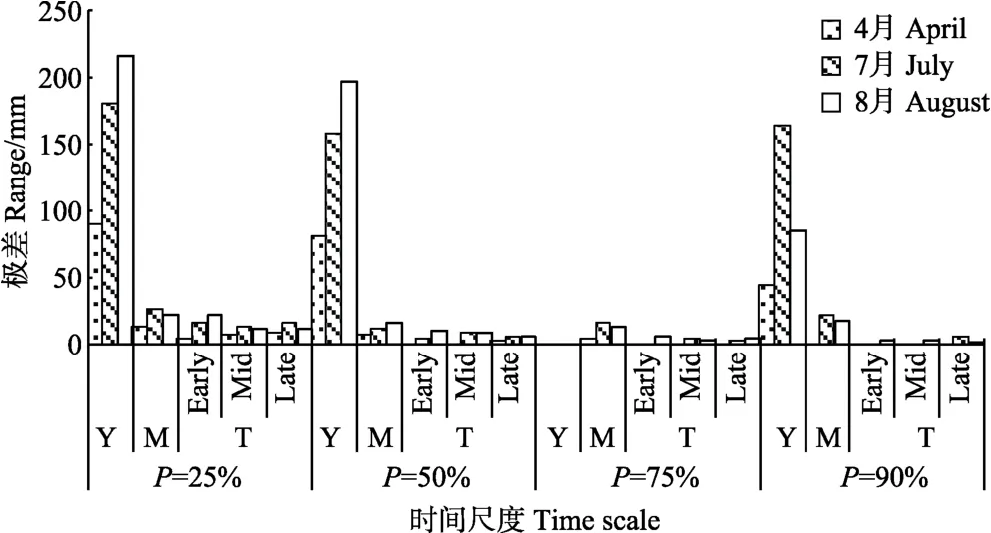
图2 不同时间尺度下的降雨量极差Fig.2 Range of rainfall under different time scales

2.1.3 旬尺度降雨量

通过对1951—2015年4月、7月、8月的上中下各旬的降水排频计算，设计时段为旬时，在频率分别为25%、50%、75%、90%的情况下，4月、7月、8月的极差变得更小。从图 2可以看出，降水极差由大到小依次为年尺度、月尺度、旬尺度。对于不同的作物，其作物需水敏感期及灌水周期也不同，故在确定典型时段时需要结合作物的实际情况选择不同的设计时段。

2.2 时间尺度对灌溉设计保证率的影响

依据自然条件、经济状况、灌水方式和作物种类等，不同国家（地区）有不同的规定。国外的灌溉设计保证率一般在 75%以上，甚至有的国家达到 98%[27-28]。中国的规范[17]规定，灌溉设计保证率需在50%～95%之间。其他相关规范及导则有对规范[17]中灌溉设计保证率的定义及要求的完全引用[29-32]，也有单独规定[33-35]，其设定值的大小主要是依据灌溉设施、种植作物及水源条件等变化。如缺水地区以旱作物为主时，灌溉设计保证率取值可以低一些；丰水地区以水稻为主时，其值需要高一些；同一地区，水田的灌溉设计保证率比旱田高一些。利用先进的灌溉设施灌溉经济作物时，灌溉保证率高一些；对于园林绿地植物，选定中等干旱年作为设计标准，在保证工程较强的适应能力的同时，也使得工程具有合理的投资。在具体计算灌溉设计保证率时，还需考虑灌溉取水工程有、无径流调节措施。

从各种规范、标准、导则中可以看出，灌溉设计保证率较少涉及其时间尺度，多以年降雨量排频进行分析，选择了年作为计算时间尺度，默认了来水量可以在不同计算时段内实现完全调节，使得来水量完全能够被灌溉所利用。事实上，当以年为单位时，来水量的计算就是以年调节为前提条件，而作物灌溉则以作物生育期、季或旬为时间单位，其需水调节也达不到年调节，这就出现了典型年选择的时间尺度与作物灌溉需要不匹配的矛盾。

同时，在没有工程调节措施时，作物的需水量调节是以根区土壤有效库容为基础，结合作物需水量、气象条件、灌水周期等实现灌溉水量的有限调节，与上述同时段的来水量也不能完全保持一致。因而，利用降雨或来水量进行灌溉设计保证率计算，存在供需水时间尺度不同步的现象。

2.3 时间尺度对灌溉制度的影响

在制订河南省节水农业重点实验室试验田的冬小麦和夏玉米的灌溉制度时，依然用典型年法来确定其典型年。P=25%时，典型年分别为2005、1985和1994；P=50%时，典型年分别为1982、1961和1976；P=75%时，典型年为1989；P=90%时，典型年分别为1959、1966和1988。将典型年中的降雨分成不同时间尺度（由大到小依次为季尺度、月尺度、旬尺度、日尺度），利用不同的降雨尺度来拟定各自的灌溉制度。

根据水量平衡法计算得出不同典型年冬小麦及夏玉米的灌溉制度，由小麦各生育期的计划湿润层深度计算土层允许储水量的上下限，作物灌溉定额、生育期内的降水利用量及作物需水量（该处定义需水量为作物灌溉定额和生育期内的降水利用量之和）见图3。

由图 3可知，灌溉设计保证率相同时，不同时间尺度下，典型年各年份的需水量差异均不大，但灌溉定额和降雨利用量均有差异。在不同灌溉设计保证率下，随着时间尺度的减小，冬小麦和夏玉米灌溉定额呈现下降趋势，相应的降雨利用量呈现增长趋势。这表明冬小麦和夏玉米的灌溉定额与降雨利用量是一种互补关系，即降雨利用量少，灌溉定额就多；反之，降雨利用量多，相应的灌溉定额就少。

不同时间尺度下的年灌溉定额及年降雨利用量如表3所示。采用方差分析研究时间尺度对灌溉定额和降雨利用量影响的显著性，检验水平α为0.05。

由表3可知，在灌溉设计保证率为25%时，季尺度下的年灌溉定额显著高于日尺度下的年灌溉定额，日尺度下的年灌溉定额较季尺度、月尺度和旬尺度分别降低了34%、23%和3%。季尺度和月尺度下的降雨利用量均显著低于日尺度下的降雨利用量。这说明在制定灌溉制度时，丰水年采用季尺度有可能造成降雨量浪费，降雨计算的时间尺度不适合采用季尺度。在偏枯水年（P=90%），随着时间尺度的减小，年降雨利用量呈上升的趋势，季尺度均明显低于旬、日尺度，年灌溉定额呈下降趋势，但差异不明显。说明随着降雨的计算时间尺度减小，降雨越来越充分得到利用，将会节省一定的灌溉水量。

图3 不同时间尺度下作物需水量、灌溉定额及降雨利用量Fig.3 Crop water demand, irrigation quota and rainfall utilization under different time scales

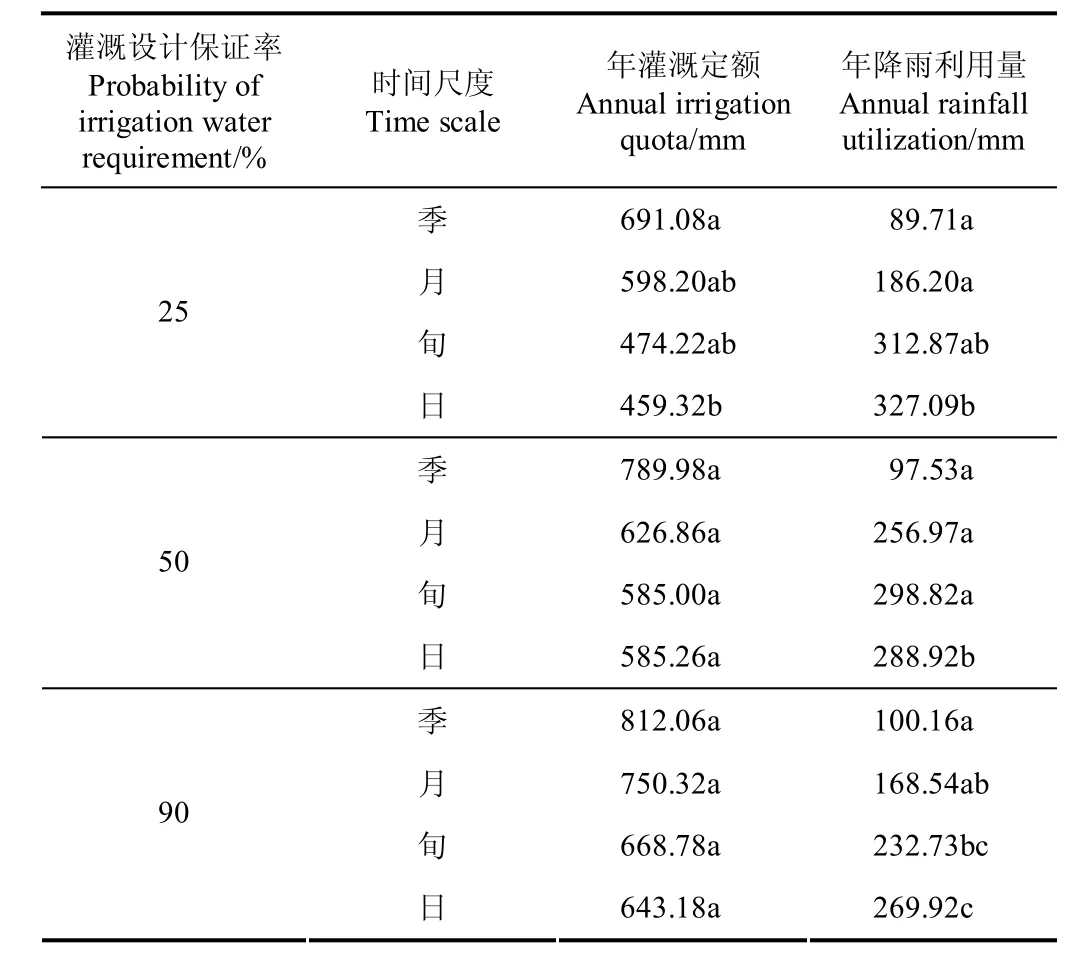
表3 不同时间尺度下年灌溉定额及年降雨利用量均值Table 3 Average annual irrigation quota and annual rainfall utilization under different time scales

但是，采用的降雨计算时间尺度并不是越小越好。由于降雨的随机性，未来降雨在选定的尺度下可能发生提前或推迟的现象，尺度越小，对应降雨区间越小，降雨发生在该区间的可能性越小，故降雨计算时间尺度越短，降雨时间精准性程度越低，从而使得灌溉设计保证率的保证程度降低。故在缺乏调节措施时，要兼顾降雨利用率和灌溉设计保证率的实现程度，建议小规模的小型农田水利工程的计算时间尺度可以增加旬或月分析。

3 结 论

利用河南省郑州市1951—2015年的降雨资料，按年降雨量和作物需水关键期对应的月降雨量、旬降雨量，分析了灌溉设计保证率的时间尺度效应。同时按照规范，选出不同灌溉设计保证率对应的典型年，分析了不同的降雨计算时间尺度下对应的典型年；采用水量平衡法，制定了作物灌溉制度，对比分析不同典型年的灌溉定额及降雨利用量的差别。得出以下主要结论：

1）针对中国大部分地区位于季风气候区，降水季节性明显，年内分布不均等特点，采用月、旬等小尺度选择典型年，在一定程度上解决了降雨的时间分布不均问题，可以提高作物生育期内降雨利用率。

2）不同时间尺度下，河南郑州地区典型年冬小麦-夏玉米连作的灌溉制度存在差异。随着时间尺度的减小，年灌溉定额呈下降趋势，而年降雨利用量表现出上升趋势。在 25%灌溉设计保证率下，季尺度下的年灌溉定额显著高于日尺度，日尺度下的年灌溉定额较季、月和旬尺度分别降低了34%、23%和3%；偏干旱年灌溉定额随降水计算尺度减小而减小，但差异不明显。

3）灌溉设计保证率选择的依据是各相关规范、标准、规程、导则等，各规范对灌溉设计保证率的规定主要参照《灌溉与排水工程设计规范》（GB50288—99）的要求，虽然有明确灌溉设计保证率定义、选择及计算，但总体上对时间尺度效应考虑不足。在大力推动节水灌溉事业的今天，时间尺度的长短会影响其保证程度，且不同的时间尺度具有不同的节水潜力与效果。若能选择合适的时间尺度，既能保证灌溉设计保证率的保证程度，又能很好的利用各种水资源，对于促进节水灌溉事业发展大有帮助。

4 展 望

目前，对灌溉设计保证率的理解和认识尚不完善，如采用作物生育关键期的月尺度或旬尺度来制定灌溉制度，重点需要从以下几个方面来考虑：1）灌溉设计保证率与作物需水敏感期相结合，保证在作物需水敏感期的灌水；同时，从作物对水的反应机制上入手，考虑调亏灌溉，协调土壤-植物-大气之间的关系，提高水分利用效率。2）灌溉设计保证率与作物的灌水周期相结合，以便于指导灌溉管理工作；3）考虑灌水方式和灌水技术等的影响；4）经济性评价，如何选择灌溉设计保证率使得经济效益最佳，需要利用经济分析的方法。

同时，在天气预报日益精准的今天，能否结合其中、短期预报成果来制定灌溉制度，以使得小尺度的降雨量及降雨时间更精准，有待深入研究。

[1]康绍忠，胡笑涛，蔡焕杰，等. 现代农业与生态节水的理论创新及研究重点[J]. 水利学报，2004(12)：1－7.Kang Shaozhong, Hu Xiaotao, Cai Huanjie, et al. New ideas and development tendency of theory for water saving in modern agriculture and ecology[J]. Journal of Hydraulic Engineering,2004(12): 1－7. (in Chinese with English abstract)

[2]康绍忠. 水安全与粮食安全[J]. 中国生态农业学报，2014，22(8)：880－885.Kang Shaozhong. Towards water and food security in China[J]. Chinese Journal of Eco-Agriculture, 2014, 22(8):880－885. (in Chinese with English abstract)

[3]Wallender W W, Grismer M E. Irrigation hydrology:Crossing scales[J]. Journal of Irrigation & Drainage Engineering, 2002, 128(4): 203－211.

[4]许迪. 灌溉水文学尺度转换问题研究综述[J]. 水利学报，2006，37(2)：14l－149.Xu Di. Review on scaling study in irrigation hydrology[J].Journal of Hydraulic Engineering, 2006, 37(2): 14l－149. (in Chinese with English abstract)

[5]谢先红，崔远来，代俊峰，等. 农业节水灌溉尺度分析方法研究进展[J]. 水利学报，2007，38(8)：953－960.Xie Xianhong, Cui Yuanlai, Dai Junfeng, et al. Review on scaling analysis approaches for agricultural water saving irrigation[J]. Journal of Hydraulic Engineering, 2007, 38(8):953－960. (in Chinese with English abstract)

[6]代俊峰，崔远来. 灌溉水文学及其研究进展[J]. 水科学进展，2006，19(2)：294－300.Dai Junfeng, Cui Yuanlai. Progress in study of the irrigation hydrology[J]. Advances in Water Science, 2006, 19(2):294－300. (in Chinese with English abstract)

[7]Schulze R. Transcending scales of space and time in impact studies of climate and climate change on agrohydrological responses[J]. Agriculture Ecosystems Environment Environ,2000, 82: 185－212.

[8]崔远来，董斌，李远华，等. 农业灌溉节水评价指标与尺度问题[J]. 农业工程学报，2007，23(7)：1－7.Cui Yuanlai, Dong Bin, Li Yuanhua, et al. Assessment indicators and scales of water saving in agricultural irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(7): 1－7.(in Chinese with English abstract)

[9]董斌，崔远来，李远华. 水稻灌区节水灌溉的尺度效应[J].水科学进展，2005，16(6)：833－839.Dong Bin, Cui Yuanlai, Li Yuanhua. Scale effect of water saving in rice-based irrigation system[J]. Advances in Water Science,2005, 16(6): 833－839. (in Chinese with English abstract)

[10]魏新光，陈滇豫，汪星，等. 山地枣林蒸腾主要影响因子的时间尺度效应[J]. 农业工程学报，2014，30(17)：149－156.Wei Xinguang, Chen Dianyu, Wang Xing, et al. Time scale effect on main factors that influence juju by transpiration in hillside jujube orchard[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2014, 30(17): 149－156. (in Chinese with English abstract)

[11]陈鹤，杨大文，吕华芳. 不同作物类型下郑珊发时间尺度扩展方法对比[J]. 农业工程学报，2013，29(6)：73－81.Chen He, Yang Dawen, Lü Huafang. Comparison of temporal extrapolation methods for evapotranspiration over variant underlying croplands[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2013, 29(6): 73－81. (in Chinese with English abstract)

[12]夏浩铭，李爱农，赵伟，等. 遥感反演蒸散发时间尺度扩展方法研究进展[J]. 农业工程学报，2015，31(24)：162－173.Xia Haoming, Li Ainong, Zhao Wei, et al. Review of temporal scale expansion for evapotranspiration retrieved by remote sensing data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2015, 31(24): 162－173. (in Chinese with English abstract)

[13]张宝忠，许迪，刘钰，等. 多尺度蒸散发估测与时空尺度扩展方法研究进展[J]. 农业工程学报，2015，31(6)：8－16.Zhang Baozhong, Xu Di, Liu Yu, et al. Review of multi-scale evapotranspiration estimation and spatiotemporal scale expansion[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015,31(6): 8－16. (in Chinese with English abstract)

[14]周祖昊，贾仰文，王浩，等. 大尺度流域基于站点的降雨时空展布[J]. 水文，2006，26(1)：6－11.Zhou Zuhao, Jia Yangwen, Wang Hao, et al. Interpolating precipitation in space and time in large-scale basin based on rain gauges[J]. Journal of China Hydrology, 2006, 26(1):6－11. (in Chinese with English abstract)

[15]崔远来，袁宏源，李远华. 考虑随机降雨时稻田高效节水灌溉制度[J]. 水利学报，1999，30(7)：40－46.Cui Yuanlai, Yuan Hongyuan, Li Yuanhua. The optimum irrigation scheduling for rice with stochastic rainfall under limited water supply[J]. Journal of Hydraulic Engineering,1999, 30(7): 40－46. (in Chinese with English abstract)

[16]沈佩君，郭元裕，刘洪先，等. 灌溉保证率的优选及其经济论证[J]. 武汉水利电力大学学报，1994(4)：351－357.Shen Peijun, Guo Yuanyu, Liu Hongxian, et al. Optimization on the design probability of irrigation works and its economic demonstration[J]. Engineering Journal of Wuhan University,1994(4): 351－357. (in Chinese with English abstract)

[17]中华人民共和国水利部 灌溉与排水工程设计规范：GB50288—99[S]. 北京：中国计划出版社，1999.

[18]尹正杰，王小林，胡铁松，等. 灌溉供水可靠度的经济设计[J]. 灌溉排水学报，2005，24(2)：52－54.Yin Zhengjie, Wang Xiaolin, Hu Tiesong, et al. Economic design of irrigation water supply reliability[J]. Journal of Irrigation and Drainage, 2005, 24(2): 52－54. (in Chinese with English abstract)

[19]周潮生，祁宗雄. 季调节灌溉工程设计保证率和设计年选择方法的探讨[J]. 水利学报，1963(5)：45－49.Zhou Chaosheng, Qi Zongxiong. Discussion on irrigation probability and design year selection methods of seasonal regulation irrigation project[J]. Journal of Hydraulic Engineering,1963(5): 45－49. (in Chinese with English abstract)

[20]蔡甲冰，刘钰，蔡林根，等. 灌区灌溉设计频率分析计算方法研究[J]. 灌溉排水，2001，20(4)：30－31,46.Cai Jiabing, Liu Yu, Cai Lingen, et al. A method of determining suitable probability for irrigation project design[J]. Irrigation and Drainage, 2001, 20(4): 30－31,46. (in Chinese with English abstract)

[21]罗高荣. 灌区灌溉保证率的概念及其计算[J]. 武汉水利电力学院学报，1991，24(1)：102－110.Luo Gaorong. Conception of the irrigation guarantee rate of irrigated area and its calculation[J]. Engineering Journal of Wuhan University, 1991, 24(1): 102－110. (in Chinese with English abstract)

[22]邹谷泉，胡采林. 灌溉设计保证率的优化选择[J]. 海河水利，1990(5)：17－23.Zou Guquan, Hu Cailin. Optimal selection of probability of irrigation water requirement[J]. Haihe Water Resources,1990(5): 17－23. (in Chinese with English abstract)

[23]王友贺，谷秀杰，师丽魁，等. 郑州市降水特征分析与水资源问题初探[J]. 气象与环境科学，2007，30(3)：61－64.Wang Youhe, Gu Xiujie, Shi Likui, et al. Preliminary study on precipitation characteristic and water resources in Zhengzhou[J]. Meteorological and Environmental Sciences,2007, 30(3): 61－64. (in Chinese with English abstract)

[24]王友贺，申双和，谷秀杰. 1965—2009年河南省降水量的时空演变特征[J]. 气象与环境科学，2011，34(3)：56－60.Wang Youhe, Shen Shuanghe, Gu Xiujie. Time-space evolution feature of precipitation in Henan Province from 1965 to 2009[J]. Meteorological and Environmental Sciences,2011, 34(3): 56－60. (in Chinese with English abstract)

[25]郭元裕. 农田水利学[M]. 北京：中国水利水电出版社，1997.

[26]陈玉民，郭国双，王广兴，等. 中国主要作物需水量与灌溉[M]. 北京：水利电力出版社，1995.

[27]Baraka T, Chamberlin, I N C. Water Supply Reliability in California[R]. Oakland: California Urban Water Agencies,1992.

[28]The Department of Water Affairs and Forestry. Water for Growth and Development in South Africa[EB/OL].2008-11-21[2008-11-24].http://www.dwa.gov.za/WFGD/documents/WfCDv6Nov21.pdf.

[29]中华人民共和国水利部 灌区改造技术规范：GB 50599-2010[S]. 北京：中国计划出版社，2010.

[30]中华人民共和国住房和城乡建设部 灌区规划规范：GB/T 50509-2009[S]. 北京：中国计划出版社，2009.

[31]中华人民共和国水利部 水闸设计规范：SL 265-2016[S].北京：水利水电出版社，2009.

[32]中华人民共和国水利部 农田水利规划导则：SL 462-2012[S]. 北京：中国计划出版社，2012.

[33]中华人民共和国水利部 喷灌工程技术规范：GB/T 50085-2007[S]. 北京：中国计划出版社，2007.

[34]中华人民共和国水利部 微灌工程技术规范：GB/T 50485-2009[S]. 北京：中国计划出版社，2009.

[35]中华人民共和国水利部 农田低压管道输水灌溉工程技术规范：GB/T 20203-2006[S]. 北京：中国计划出版社，2006.