利用于博弈论的雷达有源干扰资源分配算法
韩鹏,卢俊道,王晓丽
(中国洛阳电子装备试验中心,河南 孟州 454750)
0 引言
雷达干扰资源是现代电子战中不可或缺的一支重要力量,为了削弱敌方雷达系统的作战性能,需要运用各种技术手段干扰敌方雷达系统。但是,雷达干扰资源是有限的,如何快速合理地分配干扰资源,已成为一个决定电子战成败的重要问题。
干扰资源的优化分配问题属于非确定多项式难题[1],为此,众多学者提出了许多有效算法,如基于贴近度算法[2]、模拟退火算法[3-4]、协同拍卖算法[5]、蚁群算法[6]、遗传算法[7]等,但是利用博弈论来研究干扰资源分配问题的不多。
博弈论[8-11]是研究最优化问题的一种有效理论工具,其研究的是在同一无线环境中若干个利益冲突者进行决策来满足自身利益的问题。在近年来的研究中,博弈论作为与传统优化理论并列的一个理论工具被广泛用于无线通信等领域[12-13],取得了很多研究成果,但是在雷达有源干扰资源分配方面研究的不多。
本文基于博弈论理论探讨如何根据已探测到的敌方各雷达信息,对我方多部干扰资源进行合理分配,充分发挥作战效能,对敌方威胁目标造成最大干扰压制效果。
1 干扰效果评估指标
假定雷达干扰分队下属有N部干扰机,现有M个敌目标雷达正在对我方的通信指挥机进行监测,如图1所示。假设干扰机i最多可同时干扰Ki部雷达,各雷达的威胁系数为λj,j=1,…,M。
在干扰机的基本工作参数满足威胁雷达条件的基础之上,本文基于通信指挥机、干扰机和雷达位置分别提出干扰位置、干扰正对度以及干扰效果程度3个干扰效果评价指标,并给出了量化公式[14-15]。
1.1 干扰位置
干扰机与雷达之间的距离是影响干扰效果。因此,采用干扰位置评价指标Elij从距离上评估干扰机干扰效果。
如图2所示,干扰机的部署位置距离雷达越近,Elij越大,干扰效果越好。
1.2 干扰正对度
在对雷达进行干扰时,干扰效果受干扰机对雷达辐射主瓣的瞄准程度的影响。因此,采用干扰正对度指标Eaij从角度上评价干扰效果。
定义正对度函数为

1.3 干扰效果程度
定义干扰效果程度指标Edij,由雷达威胁半径和位置以及通信指挥机位置决定。Edij越大,干扰机的干扰效果越好。
式中:υij为干扰机i对雷达j的干扰程度,其范围是(0,1);lj为雷达j未受干扰前的探测半径;d为雷达j到通信指挥机的距离
式中:(xj,yj)为雷达j的位置坐标;(xl,yl)为通信指挥机的位置坐标。
由以上分析可知,各个干扰机对雷达j的干扰效果评估矩阵为
j=1,2,…,M.
定义向量Ω=(ω1,ω2,ω3)为干扰效果指标权重,且有ω1+ω2+ω3=1。则雷达j受到干扰机干扰的效益为
Qj=Ω×Ej=(ω1,ω2,ω3)×
(q1j,q2j,…,qNj),
(6)
则雷达总体干扰效益矩阵
式中:qij表示干扰机i干扰雷达j获得的效益。
定义雷达干扰资源分配的目标函数:
(8)
2 干扰资源分配博弈模型

本文以最大化所有干扰机收益为目标,因此干扰策略选择的竞争最优问题可以用式(10)表示为

(10)
式中:R-i表示除了干扰机i之外所有干扰机的干扰策略;Co1表示干扰机i同时最多干扰Ki部雷达。
不满足Co1限制的干扰策略不会被选择,然而干扰机很难提前知道哪些干扰策略不满足Co1限制,所以不能直接采用U作为干扰机的收益函数。为此,定义每个干扰机的收益函数为
从博弈论的观点来看,N个干扰机构成博弈参与者,干扰策略集构成纯策略空间,干扰机的收益函数构成博弈参与者的收益函数,则干扰机干扰策略选择行为可以被看作是一个博弈GE。
GE=[N,{Ri}i∈N,{ui}i∈N],
(12)
式中:N为干扰机的集合;Ri为干扰机的纯策略空间;ui为干扰机i的收益。
设up定义为
则可以得到以下结论。
结论1. GE是一个势博弈,其势函数为up。

在公式(14)中,用Φ代替up,则博弈GE满足文献[16]对势博弈的定义:

(15)
因此,GE是一个势博弈,Φ=up是它相应的势函数。
由于存在Co1限制,不是每一个纳什均衡解都满足Co1限制,因此需要分析纳什均衡的可行性。
结论2. 如果存在一个ξK满足条件
那么不满足Co1限制的干扰策略不会是博弈GE的纯策略纳什均衡。其中

(17)

对于任意一个干扰策略Ri≠0,
当Ri=0时,
ui(0,R-i)=U(0,R-i)+ξKΘ(Kj)=U(0,R-i).
(19)
从式(18)到(20)可得
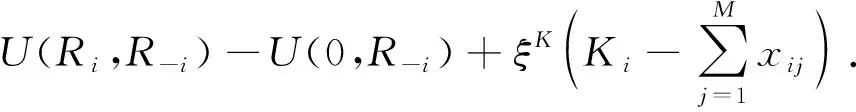
(21)
由式(16),(17)可知,ui(Ri,R-i)-ui(0,R-i)<0,即ui(Ri,R-i) 下面分析纳什均衡的存在性。 设GC的定义为 则显然不会存在另一个干扰策略组合{Ri}i∈N⊂{Ri}i∈N使得 (24) 结论4. 博弈GE最少具有一个可行的纯策略纳什均衡。 本文基于最佳动态反应设计一个低复杂度的迭代干扰策略选择算法(iterative jamming strategy selection,IJSS)来求解所设计博弈的纯策略纳什均衡,具体描述如图3所示。 因此,该算法的迭代过程是一个非递减的过程,一定会经过有限次的迭代后收敛。 下面我们分析IJSS算法的复杂度,并与穷举法进行对比。 随着干扰机和雷达数量的增加,IJSS算法和穷举法复杂度对比如表1所示(t=4),其中A(N;M;Ki)表示系统中由N个干扰机,M个雷达,干扰机i可以同时干扰Ki部雷达。从表1可以看出,IJSS算法复杂度随着N,M的增加成线性增长,而穷举法则随着N,M的增加成指数变化。因此,与穷举法相比,IJSS算法能够显著地降低计算复杂度,避免计算时造成大量的内存溢出,尤其是当系统中干扰机和雷达数目较大时。 表1 算法复杂度对比(t=4)Table 1 Comparison of algorithm complexities (t=4) 假设系统中有12部雷达,随机分布在以(100,0),(300,0),(100,150),(300,150) km为顶点的矩形区域内。有5部干扰机,随机分布在以(100,300),(400,300),(100,450),(400,450) km为顶点的矩形区域内,雷达的威胁系数分别为0.898 8,0.273 4,0.646 3,0.131 3,0.725 9,0.437 1,0.540 0,0.124 4,0.310 8,0.519 5,0.310 8,0.519 5。每个干扰机最多能同时干扰3部雷达。通信指挥机的坐标为(200,600),Ω=(0.3,0.4,0.3)。 图4为干扰机和雷达数量不同时,IJSS算法收敛速度的对比。从图中可以看出,IJSS算法具有很好的收敛性,当干扰机和雷达数量较少时,只需迭代两三次即可收敛,收敛速度很快。 表2 干扰机干扰策略选择过程 (A(4;10;3))Table 2 Process of jamming strategy selection (A(4;10;3)) 图5为不同干扰机数量情况下不同算法的性能对比,其中“随机选择算法”是指干扰机随机选择干扰策略。从图5中可以观察到,不论雷达数量多少,IJSS算法性能远优于随机选择算法,且非常接近穷举法。之所以IJSS算法的性能不如穷举法,主要原因是本文利用博弈论求解的纳什均衡解是帕累托最优解,不是全局最优解。通过图4,5说明IJSS算法在低复杂度前提下具有较好的性能。 本文利用博弈论研究了雷达有源干扰资源分配问题,提出了迭代干扰策略选择算法,为求解雷达干扰资源分配数学模型提供了新的思路。尽管迭代干扰策略选择算法与穷举法相比性能有所下降,但是考虑到该算法的复杂度较低,并且有很快的收敛速度,在电子对抗干扰资源分配上有很好的适用性。因此,该分配算法在电子对抗实时决策系统中具有一定的应用价值。






3 算法设计
3.1 迭代干扰策略选择算法


3.2 算法复杂度分析

4 仿真与分析


5 结束语

