要地防空作战中防空武器掩护能力评估方法
代进进,李相民,薄宁,吴小鹤
(海军航空大学,山东 烟台 264001)
0 引言
海军要地是未来作战海上主战兵力的驻屯基地、前进出发基地和后方保障基地,因其地理位置和战略地位重要,必将成为敌空袭的首选目标。在未来战争中,海军要地防空作战,不仅关系到海军兵力的生存,而且对夺取战争胜利有着重要的影响[1-4]。
要地防空作战是以一定数量的远、中、近和高、中、低防空火力,对重要的固定目标实施保护的作战行动。要地防空兵力的合理配置对于充分发挥要地防空武器的作战性能获得到对保护要地的最佳保护效果起着决定性作用[5-10]。
要地防空兵力配置由防空兵力数量和位置关系决定,而确定防空兵力数量和位置关系的关键因素就是要地防空武器对要地的掩护范围[11-12]。因此,本文选取掩护范围作为掩护能力的评价指标,对掩护能力的评估方法展开研究[13-14]。
1 相关概念
如图1所示,要地中心位置位于O2,载机以零航路捷径空袭要地,其投弹圈半径为rtf,要地防空武器阵地位于O1,与要地中心距离为rb,最大杀伤半径为Rmax,最大航路捷径为Pmax。
图1中:
O2O1:方位基准线;
空袭方位角α:载机空袭方向与基准线夹角,顺时针为正,逆时针为负,α∈(-π,π];
航路捷径P:地面防空武器到载机航路水平面投影的最短距离;
掩护纵深Rn:指载机到达投弹圈前穿过要地防空火力圈的距离[15];
掩护范围φyh:指要地防空武器对载机存在掩护纵深,且航路捷径小于最大航路捷径的空袭方位角集合,即
φyh={α|Rn≥0,P (1) 如图1所示,θp为最大航路捷径所对应的来袭方位角,称为最大航路捷径方位角,取θp∈[0,π/2],其计算公式为 θj为要地中心到防空火力圈和投弹圈交点的连线与基准线夹角,称为交点方位角,取θj∈[0,π],其计算公式为[15] (1)Rmax≤rtf 1) 如图 2所示,当0≤rb≤rtf-Rmax时,可得掩护角范围: φyh=∅. (4) 2) 如图 3所示,当rb>rtf-Rmax,且θp=θj(或π-θj)时,rb取值为 掩护角范围: (6) (2)Rmax>rtf 1) 如图 4所示,当0≤rb≤Rmax-rtf时,掩护角范围计算如下: (7) 2) 如图 5所示,当rb>Rmax-rtf时,掩护角范围计算如下: 若rb≤Pmax,则 φyh=[-θj,θj]. (8) 若rb>Pmax,如图6所示,当θp=θj(或π-θj)时,rb计算同式(5)。 (9) φyh=[-θp,θp]. (10) 要地防空武器对保护要地掩护范围计算流程 如图7所示。 (1) 要地防空武器火力圈小于载机投弹圈 假设条件:载机投弹圈rtf=100 km,地面防空武器的最大杀伤距离Rmax=50 km,地面防空武器与要地中心距离rb∈[0,300] km。 当航路捷径Pmax=30 km时,掩护角范围变化如图8所示。 当航路捷径Pmax=45 km时,掩护角范围变化如图9所示。 (2) 要地防空武器火力圈大于载机投弹圈 假设条件:载机投弹圈rtf=100 km,地面防空武器的最大杀伤距离Rmax=200 km,地面防空武器与要地中心距离rb∈[0,600] km。 当航路捷径Pmax=40 km,掩护角范围变化如图10所示。 当航路捷径Pmax=80 km,掩护角范围变化如图11所示。 当航路捷径Pmax=160 km,掩护角范围变化如图12所示。 本文以要地防空作战为背景,研究了一定要地防空火力部署下,要地防空武器对保护要地的掩护范围计算方法。本文的研究有利于完善要地防空作战理论体系,对辅助要地防空作战指挥员进行阵地优化配置具有重要指导意义。2 掩护范围解算方法
3 解算流程
4 算例
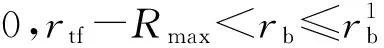
5 结束语

