准滑动模态控制在四级倒立摆的应用*

胡耀各 ，冯祖仁

（1.西安交通大学机械制造系统工程国家重点实验室，西安 710049；2.中国电子科技集团公司第二十八研究所，南京 210007）

0 引言

倒立摆系统是一个典型的多变量、高阶次、强耦合的非线性系统。从工程实际应用来讲，步态机器人的平稳控制，两轮自平衡小车平衡控制，火箭发射的姿态控制等等都和倒立摆的稳定控制有一定的相似性，因此，研究倒立摆所产生的理论方法以及结论具有很强的推广意义［1-3］。

倒立摆系统的控制方法已经十分成熟，如PID控制、LQR控制、LQY控制、模糊控制、专家控制、神经网络控制、滑模控制等。以及控制理论的综合应用如模糊专家控制、基于遗传算法的模糊控制、基于神经网络的模糊控制等。对一、二、三级倒立摆系统实现了较好的控制［4-10］，但是四级倒立摆的控制难度更大，因为状态变量更多，相关的文献较一、二、三级倒立摆系统要少很多［11-12］。

本文提出了一种新的准滑动模态控制方法，采用李雅普诺夫方法证明其稳定性，并对四级倒立摆模型进行了控制仿真。相比较于基于趋近律的滑模控制，准滑动模态控制能够有效地减弱系统状态和控制量的高频抖振。

1 四级倒立摆模型介绍

1.1 物理模型

四级倒立摆系统主要由控制对象、驱动系统以及传感系统组成。控制对象为小车与4个摆，小车与摆、摆与摆之间依次铰连接。由电机通过皮带传动驱使小车在导轨上直线运动。传感系统包括5个电位器，其中4个作为角度传感器，分别测量摆之间的相对偏角 θ4-θ3，θ3-θ2，θ2-θ1及 θ1，一个作为位置传感器检测小车位移r。系统原理结构如图1所示，几何描述如图2所示。控制目标是通过给定电机电压，对小车施加一个控制力P，保持4个摆呈竖直状态，且小车位于指定位置。

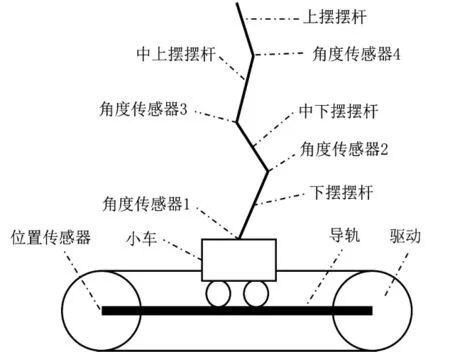
图1 四级倒立摆原理结构图

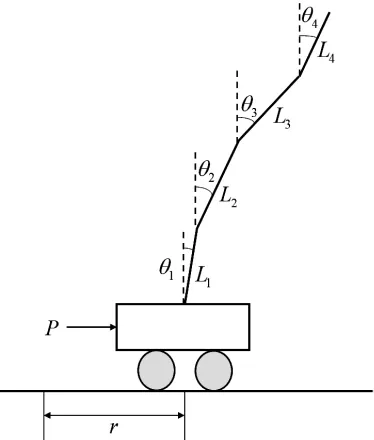
图2 四级倒立摆几何描述图

1.2 状态空间描述

选择输入为：u=e（功率放大器的输入电压）

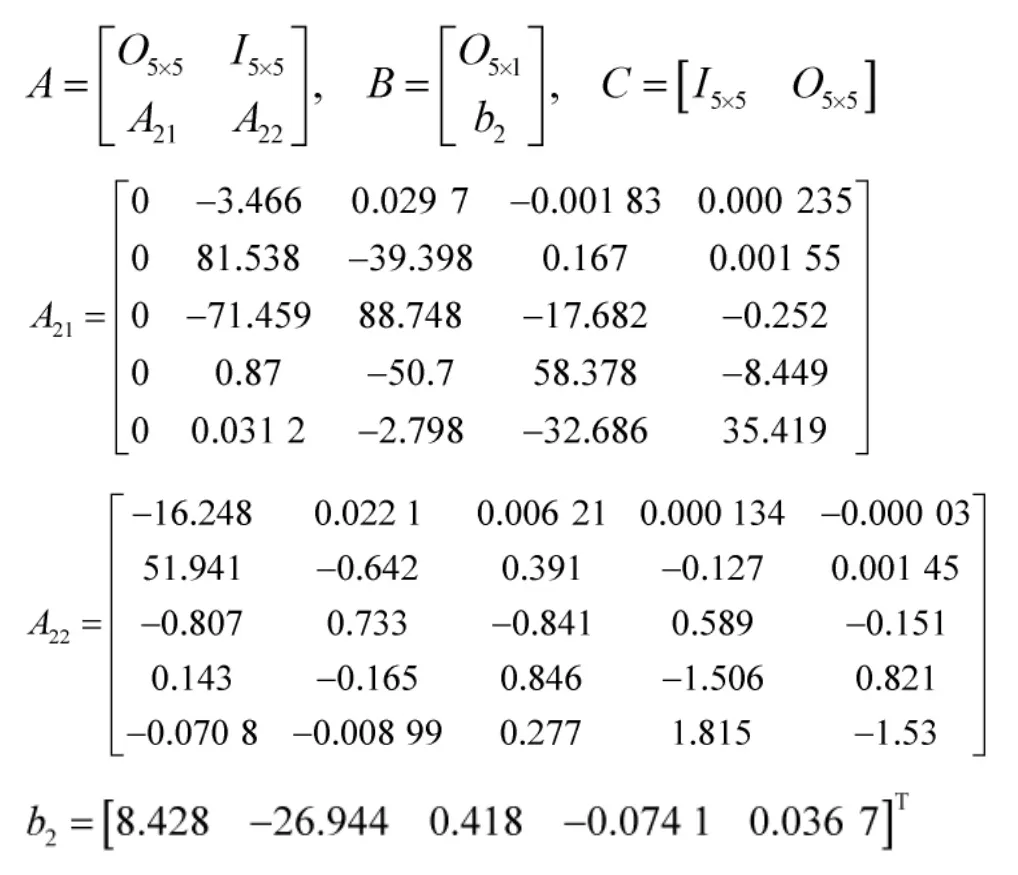
参考文献［12］可以得到四级倒立摆的状态空间方程：

其中，

1.3 稳定性和可控性分析

计算得到系统的特征值为［0，-17.316 9，-12.445 6，-9.3755，-6.3630，-3.5784，11.1250，7.3981，5.9694，3.820 0］。系统稳定的条件是特征值都位于原点左边，显然四级倒立摆是一个不稳定系统。对系统进行能控性分析，构造能控性判别矩阵M=［B，AB，AB2，AB3，AB4，AB5，AB6，AB7，AB8，AB9］。计算可得rank（M）=10，所以系统是完全能控的，可以设计控制器对四级倒立摆进行控制使其保持稳定。

2 滑模控制

2.1 滑模控制原理

滑模控制（SMC）与常规控制的区别在于控制的不连续性。这种控制可以让系统沿着预定的状态轨迹做小幅度高频率的上下运动，也就是滑模运动。滑模运动可以设计为与系统的参数和外界的扰动无关，所以具有鲁棒性。

滑模控制基本问题描述：

对于控制系统：

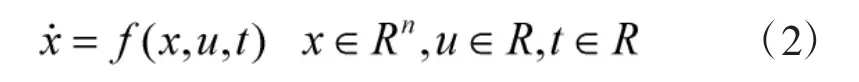
有一个确定的切换函数：

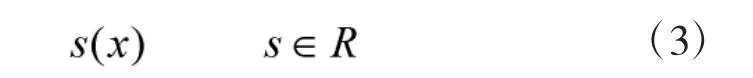
设计控制函数：

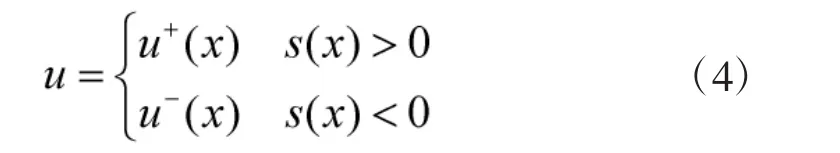
定义李雅普诺夫函数：

要使得系统稳定应该满足：

2.2 切换函数设计

采用Ackermann公式设计切换函数对倒立摆进行控制。切换函数为：

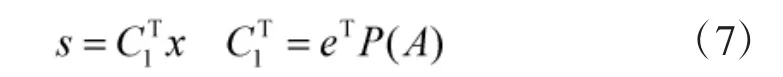
Ackermann公式：

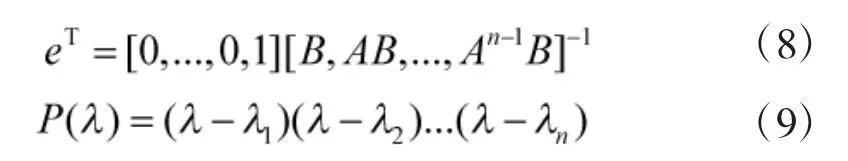
为了保证系统的稳定性应该满足：

2.3 基于趋近律的滑模控制器设计

滑模控制包含两个阶段，第1个阶段是趋近运动，即切换面外的状态趋向切换面的过程；第2个阶段才是滑模运动，即状态沿着切换面到达稳定状态。基于趋近律的滑模控制器可以对趋近运动进行限制，改善运动的特性。采用指数趋近律：

此时：

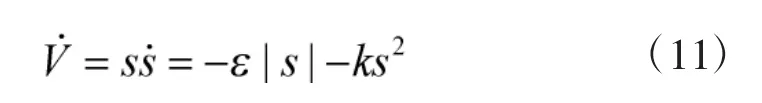
由：

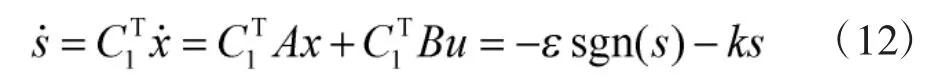
可以得到控制率：

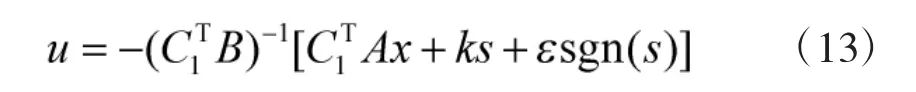
2.4 准滑模控制

理想滑模控制需要将状态点吸引至切换面，而准滑模控制只要将状态点吸引到某一个Δ邻域内，Δ邻域是切换面的边界层，在边界层内采用连续化反馈控制，在边界层外采用切换控制。准滑模控制最常用的方法是用饱和函数sat（s）代替指数趋近率中的 sgn（s）。

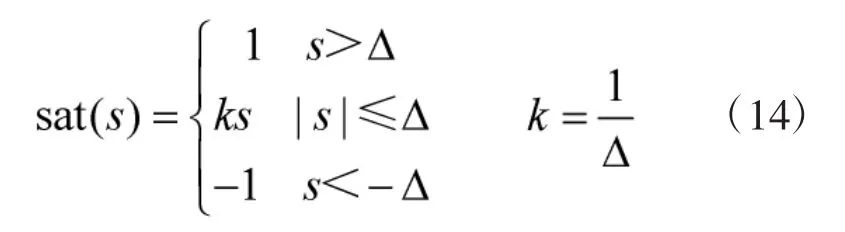
此时：

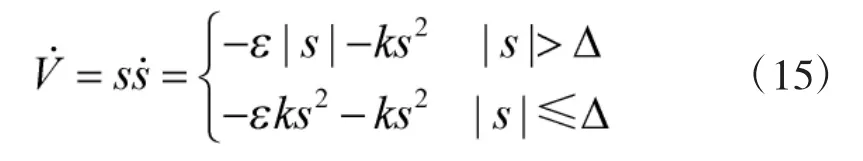
控制率：

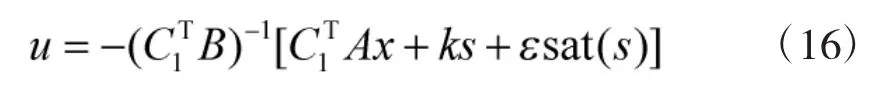
本文提出一种新的准滑模控制方法，用sig（s）代替指数趋近率中的sgn（s）。sig（s）相对于sat（s）的优点在于函数具有光滑性。

此时：

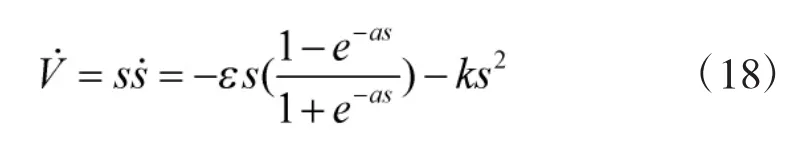
控制率：

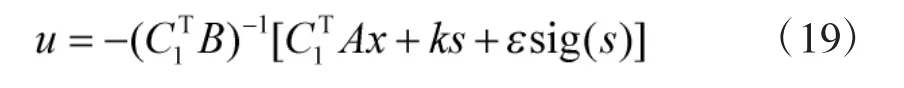
3 仿真实验

图3 指数趋近率滑模控制的状态响应

设计对照实验，对比基于趋近律的滑模控制与准滑动模态控制的控制效果。取四级倒立摆的初始状态为，期望得到的稳定状态为。系统有10个状态变量，取滑动模态控制切换面的参数。取指数趋近率的参数k=5，ε=1。取饱和函数 sat（s） 的参数 k=20。取类sigmoid函数sig（s）的参数a=50。图3是指数趋近率滑模控制的状态响应，下页图4是指数趋近率滑模控制的控制输出；图5是采用饱和函数的准滑模控制的状态响应，图6是采用饱和函数的准滑模控制的控制输出；图7是采用类sigmoid函数的准滑模控制的状态响应，图8是采用类sigmoid函数的准滑模控制的控制输出。

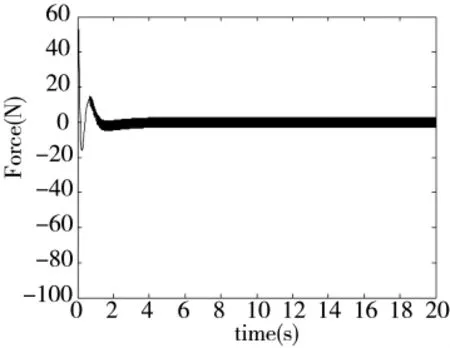
图4 指数趋近率滑模控制的控制输出

图5 采用饱和函数的准滑模控制的状态响应

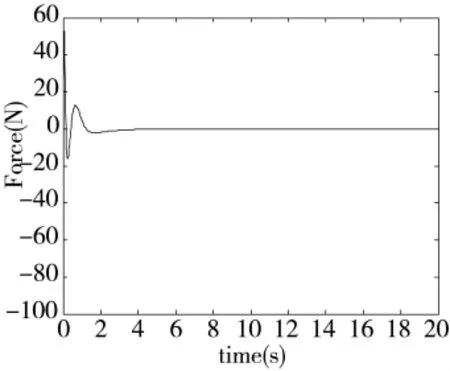
图6 采用饱和函数的准滑模控制的控制输出

图7 采用类sigmoid函数的准滑模控制的状态响应

仿真结果表明3种滑模控制都可以实现四级倒立摆的稳定控制，且都能够在4s内使倒立摆的4个摆回到稳定位置。但是指数趋近率滑模控制的系统状态和控制力都存在高频抖振，其中控制力的抖振幅值高达3 N，而两种准滑模控制都可以减弱抖振。

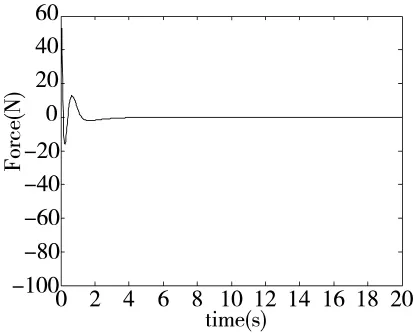
图8 采用类sigmoid函数的准滑模控制的控制输出

4 结论

本文首先介绍了四级倒立摆的物理模型和状态空间方程，并对其进行了稳定性和可控性分析。设计了基于趋近律的滑模控制器对四级倒立摆进行稳定控制，系统状态响应和控制输出具有明显的抖振，而采用饱和函数的准滑模控制和本文提出来的采用类sigmoid函数的准滑模控制都可以减弱抖振。验证了准滑模控制对于高阶倒立摆稳定控制的有效性和优越性。