不同设计参数下土工格室柔性挡墙受力及变性分析

苗满胜，刘 军

(河南高速公路发展有限责任公司， 河南 郑州 450000)

土工格室是20世纪80年代初在国际上出现的一种新型土工合成材料，其材质轻、耐磨损、伸缩自如、施工速度快并提供较高的侧向限制，广泛应用于土木工程领域。由于其结构轻、施工方便、造价低廉，能够满足绿化墙面的要求，在公路边坡防护中得到了广泛的应用[1-7]。一些学者针对土工格室柔性挡墙这种新型边坡支护结构展开了相关的研究，取得了一些成果。谢永利等[8]运用有限元分析软件MARC对土工格室柔性挡墙的工程性状进行了弹塑性数值仿真分析。宋飞等[9]运用PLAXIS软件研究了在不同高宽比、坡度及路基表面荷载下对土工格室挡墙变性性状的影响。马新岩等[10]采用数值模拟和结构计算相结合的方法，结合实际工程，对路堑土工格室柔性挡墙进行实例分析，并根据施工经验总结柔性挡墙施工工序。王根等[11]以瑞鹰高速土工格室柔性挡墙工程为背景，采用ADINA有限元数值仿真分析，考虑墙体与路基土的耦合关系，研究了土工格室多级柔性挡墙的受力机理，对比多级挡墙在多种工况下的受力情况。杨利等[12]分析了土工格室加筋粗粒土的效果分析。刘军等[13]结合工程分析了土工格室柔性挡墙的敏感因素。而在土工格室挡墙设计过程中，土工格室柔性挡墙在不同设计参数下的受力及变形规律仍不清楚，因此土压力计算方法缺少合理的理论基础，理论研究仍然落后于工程实践，需要进行深入的研究。

本文采用岩土工程有限差分软件FLAC3D计算分析了设计参数下土工格室柔性挡墙的受力及变形特征，研究了厚度、坡比以及弹性模量对于柔性挡墙受力及变形性状的影响。为柔性挡墙土压力计算方法的提出提供了理论基础，对于工程设计具有一定的参考意义。

1 模型的建立及相关参数

1.1 模型的建立

土工格室柔性挡墙数值计算模型包括几何模型与材料模型。本文根据工程实际问题和研究目的需要建立柔性挡墙计算模型。计算模型是由挡墙墙身、基础、墙后填土三部分组成。经过查阅参考资料[13]以及试算，确定各部分的模型尺寸为：挡墙长度15 m，高度为6 m，厚度为3 m，挡墙设计坡率为1∶0.5；基础宽度为4 m，厚度为1 m，墙后土体宽度取15 m。其三维实体几何模型与边界示意图分别如图1、图2所示。由于该模型采用整体挡墙的一部分进行分析，所以需要确定挡墙模型边界条件。挡土墙前立面和后立面边界施加X方向位移约束为零，挡土墙前后两两个侧面边界施加Z方向位移约束为零，柔性挡墙底面边界在X、Y、Z三个方向施加位移约束为零。

1.2 网格划分

FLAC3D数值分析过程中，单元划分越多，计算结果越精细，但是单元划分过多，会增加计算机负担，导致计算过程缓慢。综合考虑各种因素，本次计算单元网格划分采用“扫略网格划分”，将挡墙墙体作为重点研究对象，进行网格加密处理；基础部分和土体部分作为非研究重点，网格划分时相对疏一些。具体单元网格划分如图3。整个模型共17 904个节点，15 585个单元。

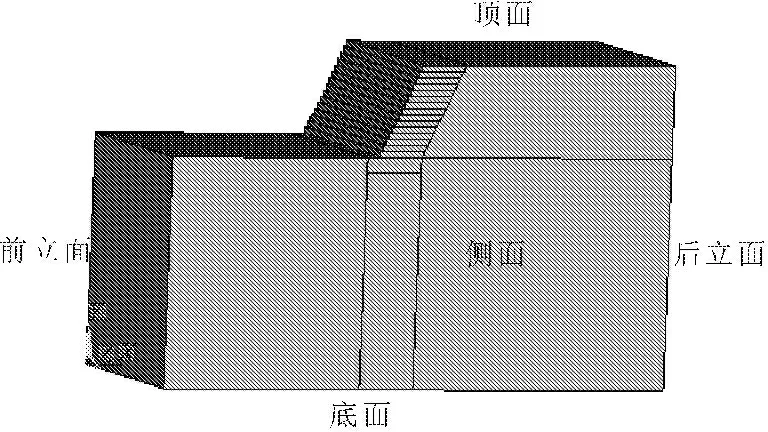
图1 几何模型示意图(单位：m)

图2 边界示意图

图3网格划分立体图

1.3 模型参数的选取

在土工格室柔性挡墙中，土体本构模型Mohr-Coulomb理想弹塑性模型，该理论比较完善且简单实用，被广泛应用于岩土工程和理论实践中[14]。FLAC3D数值分析软件中的Mohr-Coulomb理想弹塑性模型需要输入5个参数，分别为黏聚力c、内摩擦角φ、密度ρ、剪切模量G和体积模量K。其中黏聚力c、内摩擦角φ和密度ρ可以通过土样的常规试验来获取，而剪切模量G和体积模量K可根据弹性模量E和泊松比μ求得，其计算方法如式(1)所示。

(1)

参考工程实际勘察报告及课题组试验结果对柔性挡墙强度参数取值，挡墙各部分具体参数见表1。

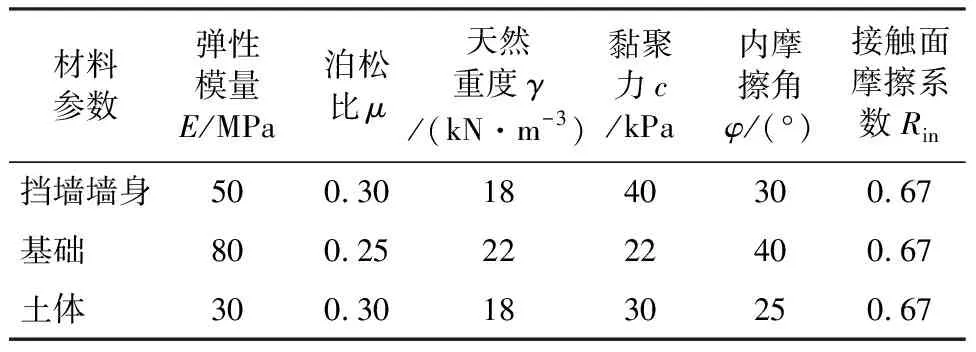
表1 模型材料计算参数

1.4 接触面优化

本文对挡墙墙体、地基基础以及墙后填土相连接的结构面采用接触面形式处理，即采用FLAC3D软件中自带的Interface接触单元来模拟[15-16]。Interface接触单元厚度为零，但具有方向性，是通过将三角形面积单元分配到各节点上来表示的，在设置接触面单元时需要Interface单元平铺到事先确定的目标面上，并与另一个接触面连接在一起。

接触面上受到的切向力小于最大切向力时处于弹性阶段，可通过式(2)和式(3)来确定其某一时刻的法向力与切向力。

Fn(t+Δt)=KnμnA+σnA

(2)

(3)

当|Fs|=Fsmax，接触面滑动时，切向力保持不变，进入塑性变形阶段，法向应力随着位移增大而增大，可按式(4)计算。

(4)

2 工程实例计算

2.1 初始应力平衡

土工格室柔性挡墙建造之前，施工场地地表位移为零，但是土体内的应力却是一直存在的，这种没有位移只有应力存在的状态即地应力平衡状态。数值模拟过程中，初始应力平衡是为了使数值模型获得一个存在初始应力但初始应变为零的状态。考虑到柔性挡墙施工场地中自重应力是主要初始应力，显然其自重应力是外力，地应力场是将自重应力下的场地内力提取出来施加于数值模型上，开始工程数值计算时再施加自重应力，使得场地内的内力与外力平衡从而获得较精确的、没有受到人为因素干扰情况下的数值模型初始状态。

边坡坡体在自重应力下的水平有效应力与水平位移见图4和图5。

2.2 水平土压力及变形对比分析

基于前文分析成果，并将数值模拟计算结果同现场测试和模型试验进行对比。土压力数值模拟结果与对比曲线见图6、图7。水平位移数值模拟与曲线见图8、图9。

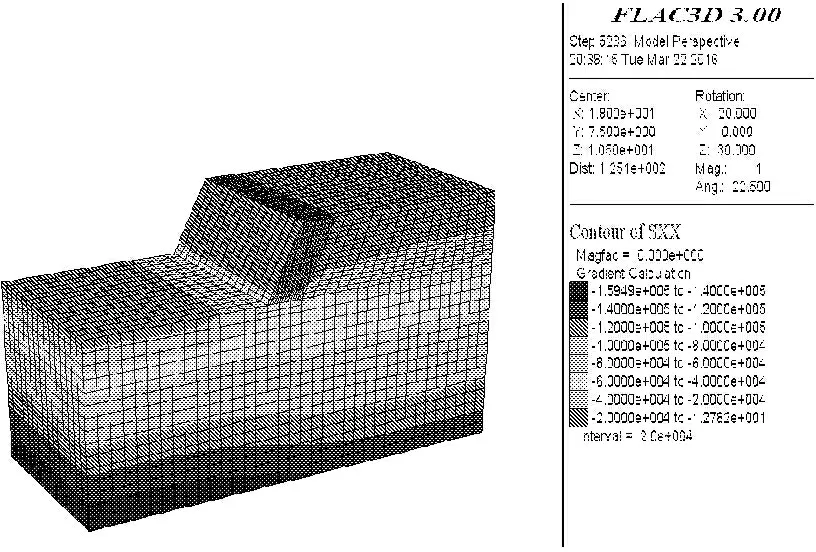
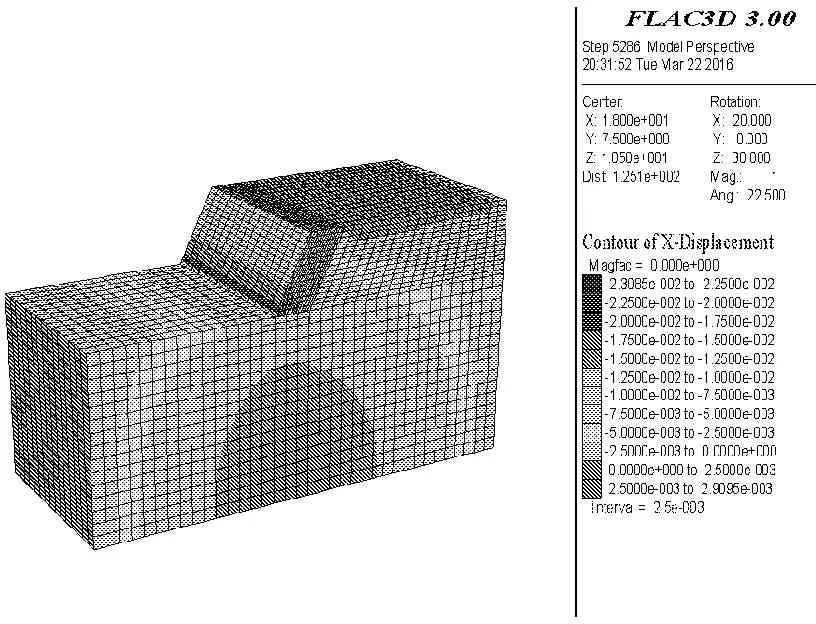
图4 重力作用下的初始水平有效应力分布

图5 重力作用下的初始水平位移分布

图6 柔性挡墙墙体水平受力云图

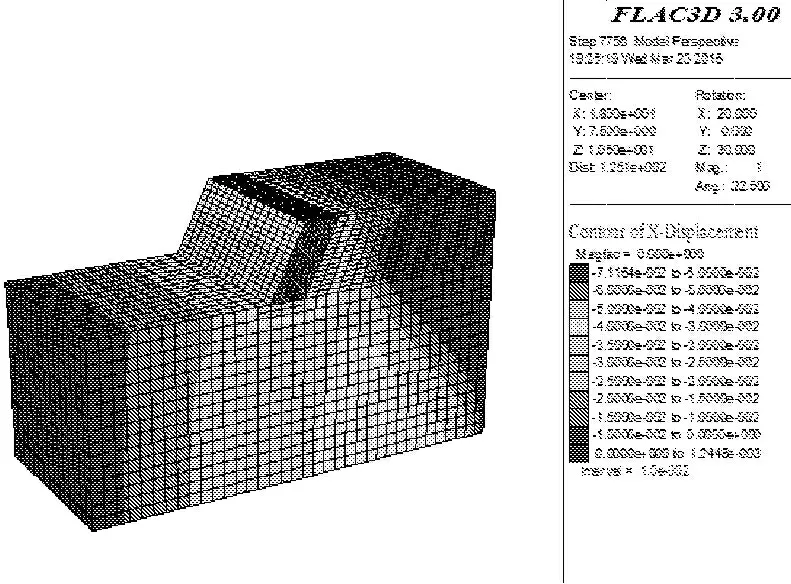
图7 柔性挡墙水平土压力数值模拟计算结果

图8柔性挡墙墙体水平位移云图

从图7中可以看处，柔性挡墙水平土压力数值计算结果与现场实测值存在一定差距，数值计算结果较实际偏小。数值计算解得最大土压力值为55.32 kPa，位于挡墙高度2.5 m位置处；而现场实测土压力值最大为57.62 kPa，且位于墙高1/2H处(挡墙高度为3 m)。这主要是由于数值分析在理想状态下建立计算模型和设定边界条件，无法完全准确模拟挡墙具体和施工机械影响，所以现场实际测量存在一定差异，而且现场实际测量除了容易受周边环境影响，还会出现一些不可避免的人为操作误差。

从图9中可以看到，柔性挡墙墙体水平位移数值模拟计算结果曲线与现场测试和模型试验基本一致，均以墙高1/2H为界，分界以上水平位移随墙高减小，分界以下沿墙高增大。数值模拟算得最大墙体位移为4.52 cm，比现场测试结果要小15.04%，比模型试验要大2.03%。则说明本文数值模拟计算结果与现场测试和模型试验结果在数值上差距不大，且曲线发展趋势也基本相似，因此可以认为本文数值分析在墙体水平位移方面比较接近实际。

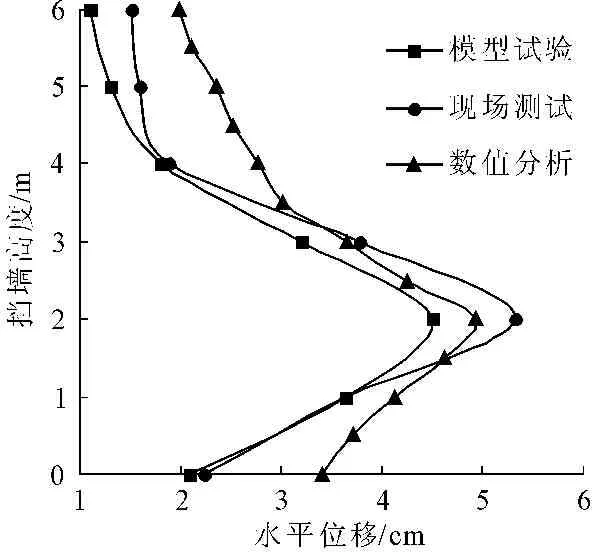
图9柔性挡墙水平位移数值模拟计算结果

3 柔性挡墙设计参数影响分析

根据前文分析可知，了解各个挡墙设计参数对于土工格室柔性挡墙的受力及变形的影响程度，对于挡墙设计及施工有着重要意义。本文选取挡墙厚度、挡墙坡比、挡墙弹性模量三个参数设立3种工况展开分析，具体如表2所示。以期把握此类参数对于挡墙受力与变形的影响，从而对挡墙设计进行优化，对挡墙土压力计算提供依据。

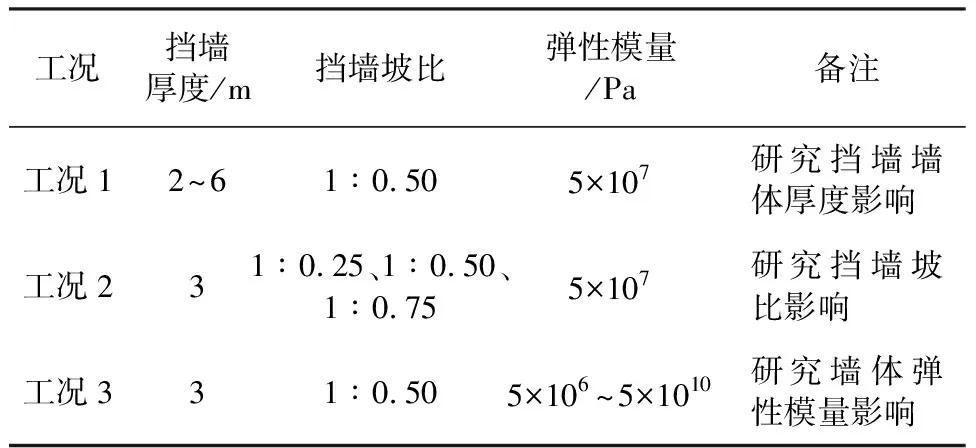
表2 数值模拟各工况设计表

3.1 挡墙厚度影响分析

图10为墙高为6 m，坡比为1∶0.5的挡柔性墙，墙身厚度在2 m到5 m范围内变化时的墙背水平应力及位移。

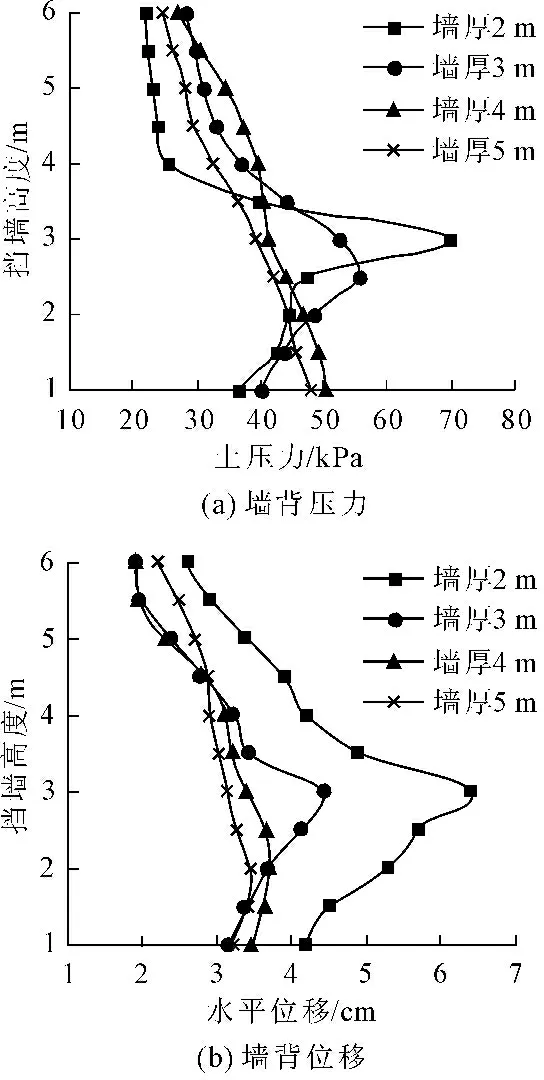
图10柔性挡墙墙体厚度变化影响图

从图10(a)中可以看出，高为6 m的柔性挡墙墙体厚度不同时，土压力沿挡墙高度分布差异较大。当墙体厚度为2 m时，挡墙水平土压力整体较小，但是在墙高为3 m位置处，土压力急剧增大，达到69.73 kPa；当墙体厚度为3 m时土压力分布较均匀，在墙高2.5 m位置处达到最大，最大为55.32 kPa；当墙体厚度为4 m和5 m时，挡墙水平土压力值相差不大，均呈不规则的线性分布，且随挡墙高度降低逐渐变大。

从图10(b)中可以看出，不同挡墙厚度下墙背水平位移曲线与土压力曲线具有一定相似性。墙厚为2 m时挡墙变形较大，尤其在墙高为3 m位置处达到6.34 cm，变形量大于挡墙厚度3%，说明2 m的挡墙厚度并不能满足该挡墙安全设计要求。墙体厚度为3 m、4 m和5 m时，挡墙墙体水平位移相差不大，这也说明在满足挡墙安全设计要求基础上，盲目增加挡墙厚度对于挡墙变形的控制有限，反而只会增大工程造价。

3.2 挡墙坡比影响分析

图11为墙高为6 m、墙厚为3 m的土工格室柔性挡墙，在变化挡墙坡比情况下的墙背土压力及水平位移曲线。

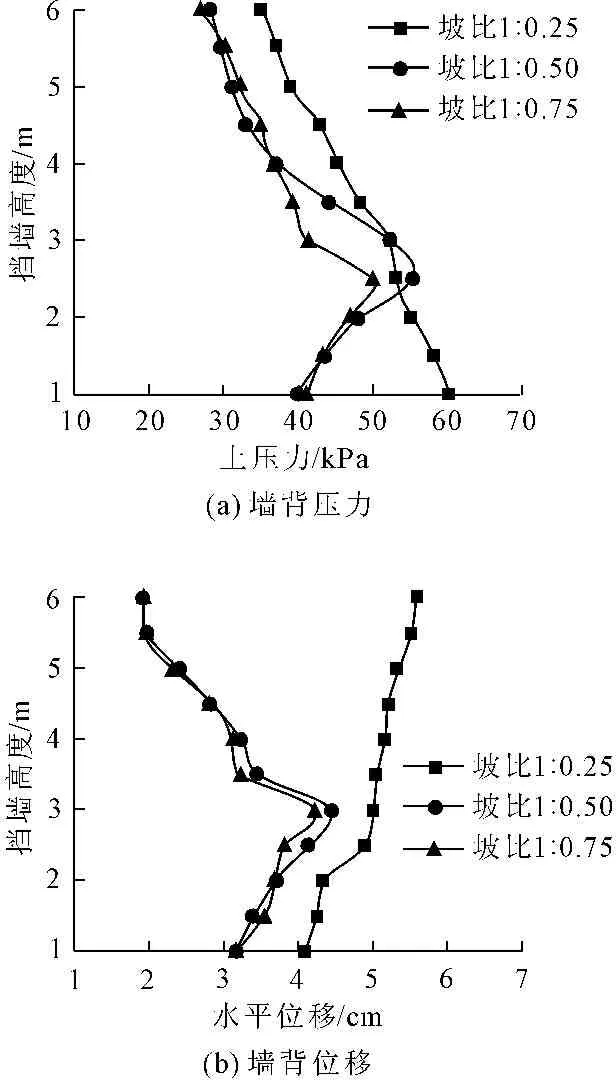
图11柔性挡墙坡比变化影响图

从图11(a)可以看出，柔性挡墙坡度越陡，挡墙水平土压力越大。挡墙坡度为1∶0.75和1∶0.50时，挡墙水平土压力分布曲线相似，均在墙高2.5 m处分界，分界以上部分，土压力沿墙高线性减小，分界以下部分恰好相反，分界点处土压力值最大，分别为55.32 kPa和49.96 kPa；柔性挡墙坡度为1∶0.25时，土压力沿墙高呈线性分布，在挡墙底部达到最大为60.11 kPa。

结合图11(a)和图11(b)可以看出，挡墙坡比在1∶0.75到1∶0.50之间时，坡比对于挡墙水平土压力及墙体位移影响不大，说明在挡墙设计过程中，可适当地在坡比1∶0.75到1∶0.50之间提高挡墙坡度，从而减少挡墙占地面积；但是当挡墙设计坡比大于1∶0.50时，要想继续增大挡墙坡来减少占地面积度则需要谨慎，因为坡比为1∶0.25的柔性挡墙墙体水平位移较大，且沿挡墙高度呈线性增大，最大位移点达到5.57 cm，说明该柔性挡墙设计较陡时，其受力形态和位移变形规律产生了较大变化，在施工过程中及施工完成后，挡墙可能还发生了绕墙顶转动的位移。

3.3 挡墙弹性模量影响分析

图12为墙体弹性模量对墙高为6 m、坡比1∶0.50、挡墙厚度为3 m的土工格室柔性挡墙水平方向土压力及墙体位移的影响。图中模量是指墙体弹性模量，取值范围为5×106Pa～5×1010Pa。

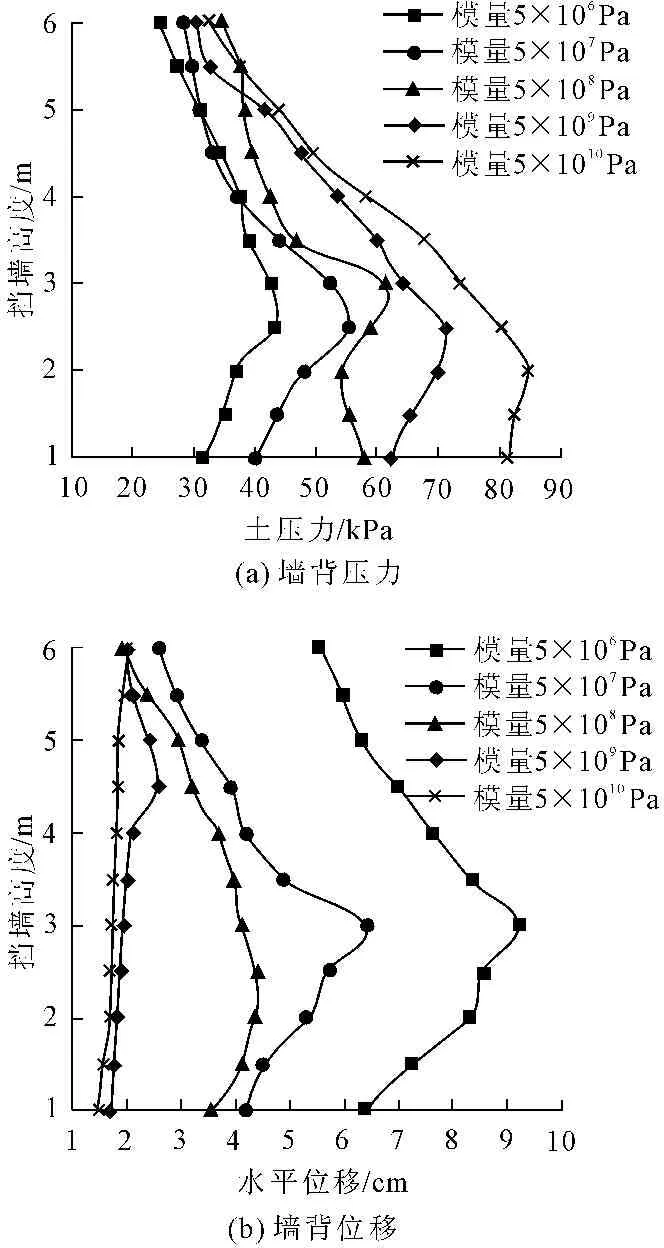
图12柔性挡墙墙身弹性模量对土压力及变形的影响

从图12(a)中可以看出，挡墙水平土压力随着挡墙墙体弹性模量的增大而增大。墙体弹性模量在5×106Pa到5×108Pa之间时，挡墙水平土压力近似呈鼓形分布，只是最大土压力值所在挡墙位置不同，墙体弹性模量为5×106Pa和5×107Pa时，最大土压力值位于墙高2.5 m处，分别为43.21 kPa和55.32 kPa；墙体弹性模量为5×108Pa时，最大土压力位于墙高3 m处为61.32 kPa。墙体弹性模量为5×109Pa和5×1010Pa时，墙体材料更接近刚性材料，挡墙土压力曲线也与刚性挡墙相似，在墙高1/3H附近处土压力值最大，分别为71.19 kPa和84.76 kPa。

从图12(b)中可以看出，柔性挡墙墙体水平位移随挡墙墙体弹性模量的增大而降低。墙体弹性模量在5×105Pa～5×107Pa之间，挡墙墙体位移呈鼓形分布，最大位移点位于挡墙中部达到9.21 cm，是挡墙厚度的3.07%，不满足设计安全要求，说明挡墙材料弹性模量过低，会导致挡墙产生较大变形，因此挡墙施工前一定要进行对格室材料进行检查验收；墙体弹性模量在5×106Pa～5×107Pa之间时，挡墙水平位移规律基本一致，呈明显非线性分布，在墙高1/2H附近处达到最大；墙体弹性模量大于5×108Pa时，挡墙墙体水平位移曲线发生了很大变化，随挡墙高度线性增加，在墙顶位置达到最大。

4 结 论

本文应用FLAC3D软件对土工格室柔性挡墙进行了数值模拟研究，分析了不同设计参数对于6 m高的路肩式土工格室柔性挡墙的受力及变形的影响，并得出了如下结论：

(1) 6 m高的柔性挡墙墙体厚度为2 m～3 m时，挡墙水平土压力和墙体位移均呈鼓形分布，最大值位于墙高1/2H附近处；墙体厚度大于3 m时，墙体水平位移变小，墙背土压力及位移曲线也逐渐过渡为线性模式。

(2) 1∶0.50和1∶0.75两种坡率的柔性挡墙其挡墙水平土压力及墙体位移曲线相似，数值相差不大，且都以墙高1/2H分界；当柔性挡墙坡比为1∶0.25时，挡墙水平土压力值及位移值，都出现了不同程度的增加，且位移曲线也近似变为直线，在墙顶位置达到最大，为5.57 cm。

(3) 6 m高的柔性挡墙水平土压力随着墙体弹性模量的增大而增大，水平位移恰好相反，随墙体弹性模量增大而减小。当体弹性模量在5×106Pa～5×108Pa之间时，挡墙土压力及墙体水平位移呈鼓形分布，在墙高1/2H附近处达到最大；当墙体弹性模量在5×109Pa～5×1010Pa之间时，水平土压力及位移曲线发生明显转变，位移曲线大致呈线性分布，土压力也变得与刚性挡墙所类似，在墙高1/3H处达到最大。