路堤荷载下水泥土搅拌桩复合地基失稳机理及其稳定性分析

聂文峰，邱邵富，张 蕊，陈 琼

(中铁二院昆明勘察设计研究院有限责任公司， 云南 昆明 650200)

目前，水泥土搅拌桩复合地基已广泛应用于高速公路软弱路基加固[1-3]。但在高填方路堤荷载作用下，针对路堤整体稳定性及其桩体失稳破坏模式的研究仍严重滞后于工程实践[4-6]。我国规范中使用的路堤稳定分析方法为极限平衡法，即根据桩体抗剪强度和桩体置换率计算复合地基的复合抗剪强度进而分析各种桩体复合地基上的路堤稳定[7-8]。但事实上，对路堤荷载作用下的水泥土搅拌桩而言，其可能发生桩体剪切破坏、弯曲破坏、受压破坏以及桩周土体绕流等[9-12]，如Kitazume M等[13]借助离心机缩尺试验指出路堤荷载下水泥土搅拌桩并非仅仅发生剪切失稳破坏，而是表现为弯曲破坏。宋苗苗[14]通过离心机试验研究了路堤荷载下素混凝土桩的破坏模式，发现路堤复合地基破坏模式较为复杂多样，包括桩体上刺破坏、坡角局部剪切破坏、路基整体剪切破坏以及倾斜挠曲破坏等。显然，确定路堤下加固桩的破坏模式是衡量路堤稳定性的关键。但是目前的传统极限平衡法不能反映路堤下桩体的真实破坏模式，进而难以准确评估路堤的稳定性。

为此，本文以某高速公路水泥土搅拌桩复合地基支撑路堤为研究对象，基于有限元强度折减法探讨了路堤荷载作用下不同位置桩体的受荷机制，籍此研究水泥土搅拌桩的失稳破坏机制及可能的失稳破坏模式。

1 传统复合地基稳定分析

目前，路堤荷载下复合地基的稳定性计算仍假定加固体和土体沿圆弧滑动面发生整体剪切破坏，如图1所示。

图1路堤稳定性圆弧滑动分析法

其中，复合地基土体综合强度指标可采用桩土面积置换率计算。复合地基黏聚力csp和内摩擦角φsp可由下述两式表达：

csp=cs(1-m)+mcp

(1)

tanφsp=tanφs(1-m)+mtanφp

(2)

式中：cs，cp分别为桩间土和桩的黏聚力；φs，φp分别为桩间土和桩的内摩擦角；m为桩土面积置换率。

虽然上述传统方法简单易用，但是其不能分析路堤荷载下桩体的内力和位移变化；且传统方法假定滑动面上的加固桩与土体的抗剪强度同时发挥，此时，路堤稳定性将被高估[10-12]。因此本文针对一具体工程实例，运用有限元强度折减法分析了路堤填筑后处于临界破坏状态下的桩土位移矢量、桩体内力以及对应的安全系数。

2 有限元强度折减法的复合地基稳定分析

所谓有限元强度折减法，就是在弹塑性有限元计算中将边坡内土体抗剪强度参数逐步折减直到其破坏为止，然后根据数值计算收敛与否、特征部位的唯一拐点以及是否形成连续贯通区作为评价标准[15-16]。

折减后的抗剪强度参数可表达为：

cr=c/Fr

(3)

tanφr=tanφ/Fr

(4)

式中：c和φ分别是土体所能提供的黏聚力和内摩擦角；cr和φr是维持平衡实际发挥的土体黏聚力和内摩擦角；Fr则是对应的强度折减系数。

2.1 数值计算模型及参数

为分析水泥土搅拌桩对路堤稳定的贡献机理，根据某高速公路水泥土搅拌桩试验段，采用ABAQUS建立一个有限元分析模型。路堤计算剖面如图2所示。试验段桩身直径0.5 m，桩长16.5 m，桩间距为1.3 m。设计路面宽度35 m，边坡比1∶1.5。路堤填土高度为4 m，分两级填筑，通过控制生死单元来模拟其堆载过程。取轴对称模型予以分析，采用接触单元来模拟水泥土搅拌桩与土体之间的相互作用，且遵循库伦定律，其中水泥土搅拌桩与淤泥质黏土的摩擦系数按当地经验取为0.2。

图2水泥土搅拌桩路堤加固剖面图

试验段典型地基土层剖面如图3所示，地基土及路堤填土均采用Morh-Coulomb模型，同时为反映水泥土搅拌桩的屈服破坏，亦采用Morh-Coulomb屈服准则。水泥土桩、填土以及地基土的材料参数可根据该高速公路试验段的勘察报告或当地经验确定，相应的计算参数如表1所示。同时为分析桩体抗剪强度对极限平衡法和强度折减法计算结果的影响，在此工程中我们取水泥土搅拌桩抗剪强度的取值区间为50 kPa～450 kPa。

图3 土层剖面图

根据前文对极限平衡法和强度折减法的概述以及具体的工程实例，图4(a)和图4(b)分别给出了有限元强度折减法计算所对应的网格、边界条件和复合抗剪强度极限平衡法所对应的计算模型。

图4两种不同方法的计算模型

为分析路堤下水泥土搅拌桩对路堤加固稳定的贡献，首先分别基于有限元折减法和极限平衡法建立一个无水泥土搅拌桩的计算模型，所得的安全系数分别为1.501与1.558，如图(5)所示。具体而言，图5(a)为有限元强度折减法所计算的位移矢量图，图5(b)为极限平衡法所得的最危险滑裂面。对比两图可知，位移矢量图的外轮廓线与最危险滑裂面基本对应，且计算所得的安全系数基本一致。

2.2 路堤稳定分析

在图2和图3的基础上，借助ABAQUS建立相应的有数值分析模型，并基于强度折减法确定其安全系数。同时根据式(1)和式(2)所确定的复合地基抗剪强度参数，并利用极限平衡法开展其稳定性评价。如前文所述，为探讨水泥土搅拌桩抗剪强度对桩体破坏模式以及路堤稳定性的影响，本文取水泥土搅拌桩的黏聚力的变化区间为50 kPa～450 kPa，为此建立9个相对应的数值计算模型。

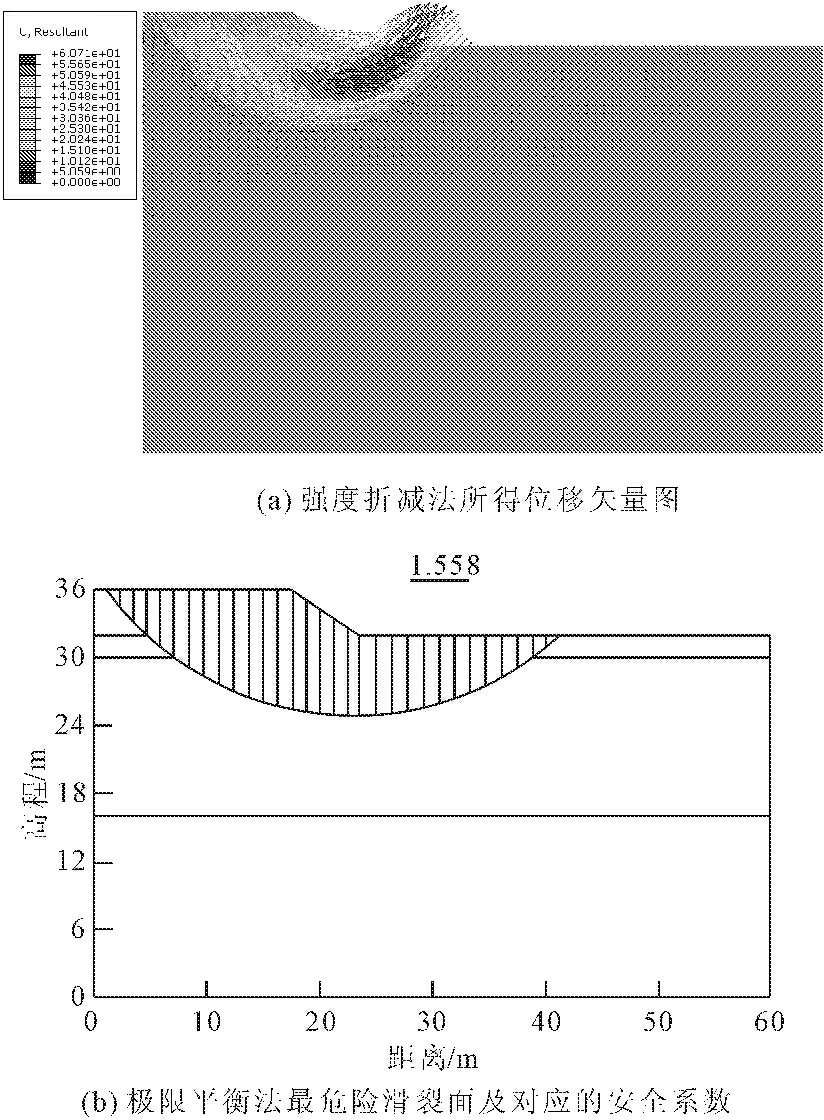
图5无桩时路堤的安全系数

为判别由强度折减法所得的路堤安全系数大小，本文采用某特征点的水平位移作为路堤失稳的判别准则。图6即为有限元强度折减法所得的水平位移与安全系数的关系。

图7为不同计算方法和路堤不同失稳判别条件下安全系数随水泥土搅拌桩黏聚力变化的曲线。由图6可知，特征点对应的水平位移均对应于一个明显的拐点，路堤安全系数随着水泥土搅拌桩抗剪强度的增加而增加，但是特征点的水平位移并未有明显的增加趋势，这说明桩体的抗剪强度对路堤稳定性有一定的贡献。由图7可知，当路堤下无加固桩时，极限平衡法与强度折减法中以不收敛和特征点水平位移为判断准则所得的安全基本相同，但是随着桩体黏聚力的增加，两种方法所得路堤安全系数均近似呈线性增加。其中，极限平衡法所得的路堤安全系数最大，且随着桩体抗剪强度的提高，其对应的安全系数逐渐趋近与以收敛作为判别准则的强度折减法所对应的安全系数；相反，以特征点水平位移为判别准则的强度折减法所得的安全系数最小，且随着桩体抗剪强度的提高，其对应的安全系数逐渐偏离以收敛作为判别准则的强度折减法所对应的安全系数。

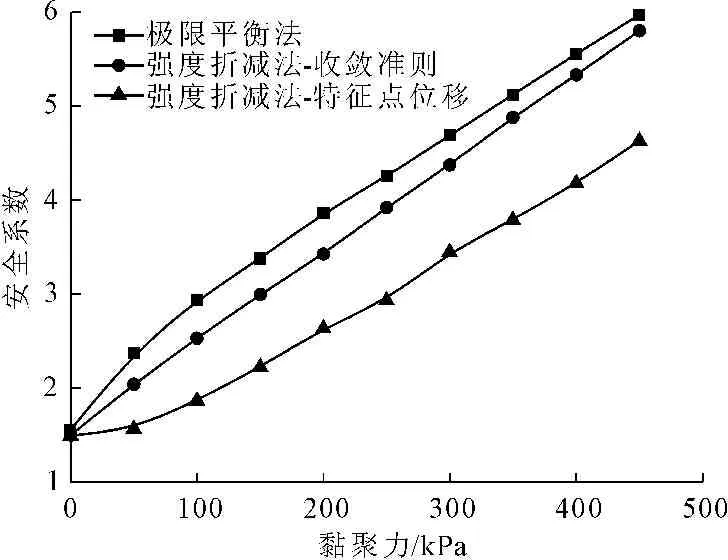
图6 安全系数与水平位移的关系

图7安全系数与黏聚力的关系

2.3 路堤下水泥土搅拌桩受荷分析

路堤荷载下不同位置的水泥土搅拌桩对维持路堤稳定的作用是不同的，不同位置的桩可能主要提供抗压、抗弯或抗剪等作用。为此，选取水泥土搅拌桩c=250 kPa的数值模型进行具体分析。图8即为相应的路堤临界失稳状态下的桩土位移矢量图。

由图8可知，左侧桩所对应的区域位移矢量以向下为主，说明此区域的桩主要承担竖向荷载；对于中间部位水泥土桩所对应的区域，其表现为向下和水平方向的位移，此部分的桩主要发挥其竖向承载作用和抗弯作用而起到阻滑效果；而右侧的桩土的位移矢量逐渐向水平方向偏转，特别是桩18#～20#所处区域的路基土体近似于水平向移动，此时桩主要承受土体的水平推力。同时相较于图5(a)可知，水泥土搅拌桩对路堤的稳定贡献主要体现于桩的存在使路堤和路基中的位移场分布不再相对集中，而是分布范围更大且最大水平位移亦显著减小，从而阻断了路堤、路基潜在滑动面的形成与贯通。

图8路堤临界失稳状态下桩土位移矢量

图9为路堤临界失稳状态下桩体最大主应力矢量图。由图9可知，水泥土搅拌桩1#～16#的最大主应力均平行于桩体方向，而边桩的最大主应力方向却发生了偏转，这就说明边坡主要承受路堤的所给的剪力。

图9路堤临界失稳状态下桩体最大主应力矢量

虽然边坡主要承受剪力，但这并不意味着路堤下桩体的失稳破坏模式为整体滑动剪切破坏。另一方面，图10给出路堤临界破坏状态下部分水泥土搅拌桩对应剪力沿桩深的分布。由图10可知，桩体剪力总体上随桩深增加趋势，且随桩体编号的增加其对应的剪力亦大致增加，其中桩19#的剪力随桩深变化最为多变。且知路堤临界破坏状态下的最大剪力仅为6 500 N左右，远远小于水泥土搅拌桩所能承受的最大剪力。

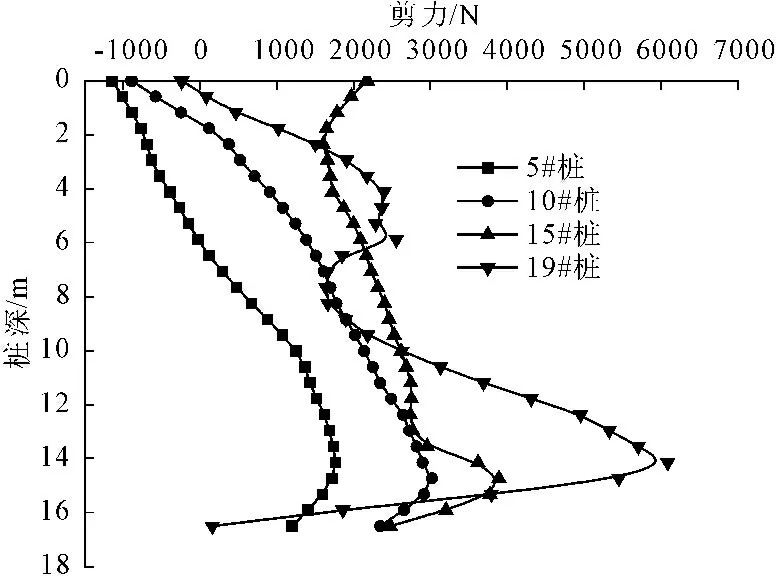
图10路堤临界失稳状态下桩体剪力

通过进一步研究，随着桩体抗剪强度的增加，对应的等效塑性应变逐渐降低，而且最大等效塑性应变所对应的位置也相应变化。且当桩体抗剪强度较大时，其更有可能发生桩体刺入破坏。

以上分析表明，路堤荷载下水泥土搅拌桩的抗剪强度并未充分发挥，其破坏模式并非像传统极限平衡法所假设的沿滑动面产生剪切破坏。

3 结 论

本文针对某水泥土搅拌桩加固的软土路基，采用有限元强度折减法研究了路堤临界破坏状态下桩土位移矢量分布和桩体剪力分布等，采用某特征点的水平位移以及收敛准则来评价路堤的整体稳定性，并将此结果与传统复合抗剪强度的极限平衡法进行了对比分析，结果表明：

(1) 在无水泥土搅拌桩加固路堤的情况下，传统极限平衡法与有限元强度折减法所得的安全系数分别为1.558和1.501，两者结果基本一致。

(2) 当存在水泥土桩加固路堤的情况时，随着桩体黏聚力的增加，两种方法所得路堤安全系数均近似呈线性增加。

(3) 在路堤荷载下，仅有边桩的最大主应力发生偏转，且路堤临界破坏状态下桩所受剪力远远小于其自身的抗剪强度，表明桩体并非发生受剪破坏；同时常规的极限平衡法不仅高估路堤的整体稳定性，而且难以反映路堤填筑下桩体的真实破坏模式。

(4) 本文着重探讨了路堤荷载下水泥土搅拌桩并非受剪切破坏，实际上由于桩体表现为较低的抗弯强度，其最有可能发生弯曲破坏。同时，还有可能发生桩间土绕流破坏，或桩体的整体倾覆破坏。而这些都有待进一步的研究，以便发展准确合理的路堤稳定计算方法。