基于需求侧响应与成本模型的风电中的储能系统运行优化

田 德，陈忠雷，邓 英

（新能源电力系统国家重点实验室（华北电力大学），北京 102206）

0 引 言

随着能源危机和环境污染问题日益严峻，风电、光伏等新能源发挥着越来越重要的作用[1-2]。但风电（wind turbine，WT）、光伏（photovoltaic，PV）的出力具有间歇性和随机性，给电网的调度带来了一定困难。储能（energy storage，ES）系统能够有效地平抑分布式电源出力的波动，发展前景良好[3-4]。根据储能的充放电特性，可以将其分为2类[5]：1）能量型储能。这类储能容量较大，容易储存，但响应速度较慢，如蓄电池、压缩空气储能等；2）功率型储能。这类储能响应迅速、可进行频繁充放电，但容量不足，如超导储能、飞轮储能、超级电容储能等。研究对象为广泛应用于配电网的能量型储能。

随着风电渗透率和储能配置容量的不断提高，如何安排风电和储能的出力，使配电网的经济效益达到最优成为了研究的热点。目前，国内外已有大量学者对该问题进行了研究。文献[6-8]分别以经济效益、环境效益、综合效益等为目标函数，通过建立优化模型给出了孤网和并网模式下的经济调度策略，但只计算配网的经济效益，没有充分考虑储能的寿命；文献[9-11]以孤立微电网最优经济运行为目标，研究了铅酸蓄电池充放电深度和次数以及储能寿命的关系，但没有考虑实时电价对调度策略的影响。随着电力市场进程的推进，受到电价政策、运行商竞争等因素的影响，优化调度不仅从电源侧进行，还考虑到需求侧响应的重要作用[12]。文献[13]在日前调度计划中考虑了负荷对不同时段电价的响应情况，基于弹性理论验证了电价型需求响应对风电消纳的作用。文献[14]在日前调度计划模型中，融入了可中断负荷和激励负荷，体现了需求侧资源的潜在调峰效益。考虑需求侧响应的特性并将其同时纳入日前调度计划，能进一步提高源荷互动的效果[15-16]。

传统的经济调度以收益最大化为原则，策略通常如下：1）由于WT发电不直接消耗燃料，不污染环境，故优先利用其出力，跟踪控制最大功率输出，若 WT功率超出负荷功率，则安排其向主网售电；2）若WT功率不足以向负荷供电，则安排ES放电，同时检测ES的状态，若满足容量约束，则增加ES出力向主网售电；3）若ES功率满发仍不满足负荷需求，则向主网购电；4）当 ES达到能量约束下限时，持续充电，直到达到能量约束上限为止。此时若出现电源功率不足的情况则向主网购电。

传统的经济调度策略存在如下几个问题：1）ES寿命和放电深度密切相关，传统策略对电池寿命不加考虑，容易对电池造成较大的损伤；2）未考虑电价的影响，如果在高峰时段，电价很高，此时如果ES容量较低，会带来较高的购电成本，从而大大降低经济效益，因此应尽量保证ES在高峰时段处于放电状态，低谷时段保持充电状态。

风储配电网优化运行是一个多目标非线性优化问题。目前的求解算法包括粒子群算法、遗传算法、蚁群算法等[17-19]。然而，这些算法在求解过程中存在局部最优、搜索能力不强等特点。微分进化算法（differential evolution algorithm，DE）[20]是由Rainer Storn和Kenneth Price在1995年提出的，是一种随机的并行直接搜索算法。它与遗传算法类似，也包括选择、杂交、变异等操作，但寻优方式不同，与传统的优化方法相比，微分进化算法具有较好的全局寻优能力。

在考虑实时电价、储能寿命和需求侧响应的基础上，采用改进微分进化算法对风储混合配电网的经济优化运行问题进行了研究，提出了优化调度模型，并进行实例研究，通过比较其他方法和该方法的经济效益，验证了模型的科学性和可行性。

1 风电/储能系统结构

传统的风储配电网模型如图 1所示。通过SCADA系统采集电网的实时风电、储能和负荷数据，并通过连接组件、通信网络上传至调度中心，完成计算功能，并将计算结果和决策下发，完成负荷功率预测、实时优化调度等功能。

图1 风电/储能配电网模型Fig.1 Wind turbine/energy storage system (WT/ES) distribution grid model

在系统中，风电和储能是主要的电源，同时和外部电网完成电能交换。通过对电源、负荷的控制调节，实现优化运行。主要关注与运行相关的关键技术，包含 2个方面：

1）需求侧响应技术

系统中，WT和ES不仅要参与供电，还要同主网进行电能交换，能量流动更加复杂。考虑到电价因素和WT的波动性，不仅要在电源侧进行优化，还需要结合负荷侧的自身特性，充分发挥可转移负荷、可中断负荷的响应特性，实现削峰填谷，降低运行成本。

2）储能技术

由于分布式电源出力的不确定性和波动性，为了实现系统稳定运行，需要安装大量的储能设备进行平抑和补偿。在制定运行策略时，既要结合电价因素实现储能的低储高发套利，同时也要考虑储能的寿命，尽量减少过度充放电，使储能的利用达到最优。

2 优化调度模型

2.1 需求侧响应模型

传统根据 WT和电负荷的短期功率预测结果，使可平移负荷（如电动汽车）、可中断负荷（如热水器）参与需求侧响应，实现分布式电源就地消纳最大化。以系统净负荷最小为目标，需求侧响应的目标函数为：

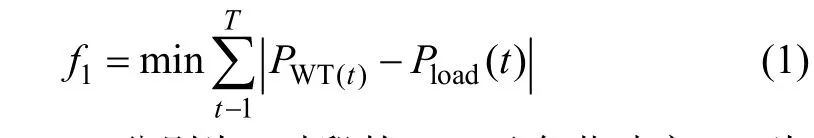
式中WT()P t、loadP 分别为t时段的WT及负荷功率；T为运行总周期，h。

响应约束包括：

1）削减量约束

式中ΔPload(t)为负荷削减量，kW；ΔPload,max(t)为最大削减量，kW； v( t)为0～1的变量，为1时表示负荷被削减，反之未被削减。

2）削减量爬坡约束

需求响应要满足爬坡约束，否则会导致负荷曲线波动性增加。

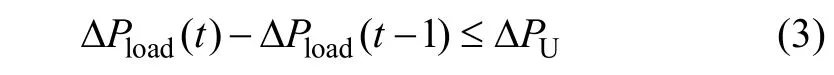
式中UPΔ为爬坡功率的上限，kW。

3）总削减量约束

整个调度期的负荷削减量应低于总的负荷可削减量，即

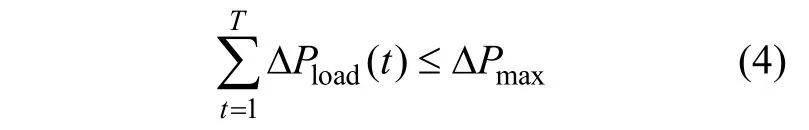
2.2 风电及储能成本模型

1）风电模型

风力发电机的输出功率是风速的函数:

WT的发电成本很低，可忽略。因此，仅需考虑WT的运行管理成本：

式中 CWT(t)为 t时段的运行管理成本，元； KWT为 WT的运行管理系数，元/kW。

2）储能模型

ES在t时段的剩余电量如下式所示：

式中 SOC(t)为 t时段 ES的剩余电量，kWh； PES(t)为 t时段ES的充放电功率，kW，当ES放电时， PES(t)大于0；当ES充电时 PES(t)小于0。η为ES的充放电效率。

对ES而言，寿命和充放电过程、温度、环境湿度等多种因素相关。本文侧重于研究储能寿命与充放电次数、充放电深度的关系。当ES充放电循环深度为R时，最大循环充放电次数NES可表示为：

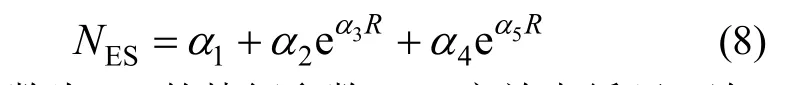
式中5个α参数为ES的特征参数。ES充放电循环1次，电池寿命损耗占总寿命百分比为1/NES，等效经济损耗成本C0为：

式中Ccost为ES的初始投资成本，元。

因此， ES等效经济损耗总成本CES为：

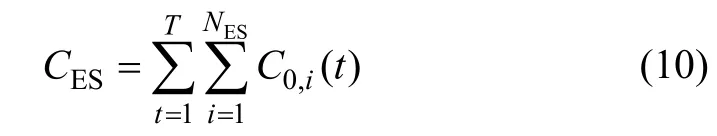
式中 C0,i(t)为第i个储能在t个控制周期内放电深度为Ri下的等效损耗成本，元；NES为储能个数。

2.3 优化调度目标函数及约束条件

经济性最优准则以系统的运行成本为目标函数：

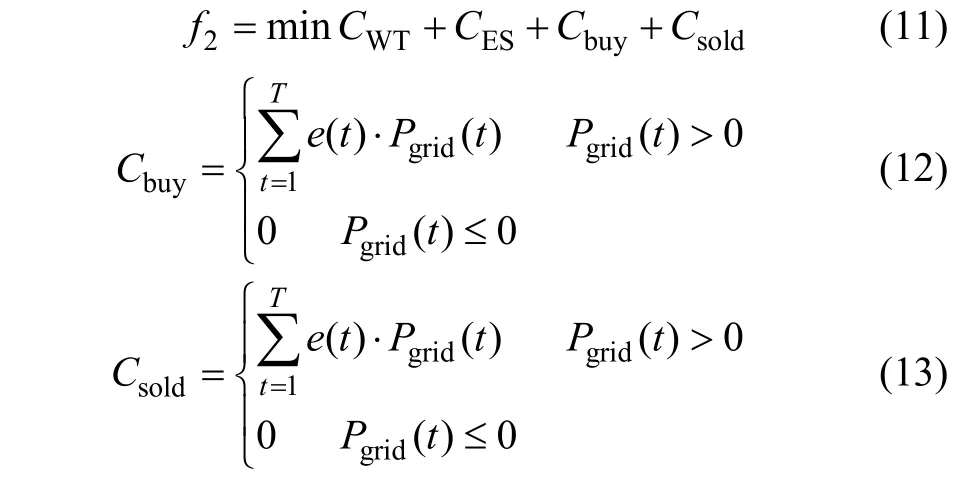
式中2f为经济效益函数，元；buyC 为系统向主网购电成本，元；soldC 为系统向主网卖电收益，元；e(t)为实时电价，元/kW；grid()P t为系统之间交换的功率，kW，当购电时为正，反之为负。

结合需求侧响应，则最终目标函数形式为：

约束条件包括：

1）功率平衡约束

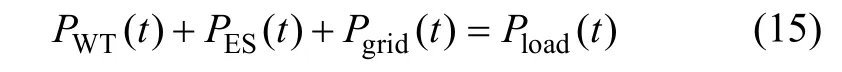
式中 Pload(t)为t时段电负荷，kW。

2）系统之间传输功率约束

式中 Pgrid,max(t)为传输功率的上限，kW。

3）ES运行约束

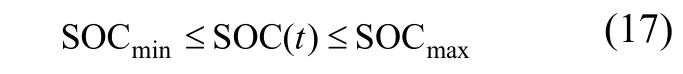
式中 S OCmin和 S OCmax分别为ES容量的下限和上限。式(15)～ 式(17)和式(2)～式(4)共同组成模型的约束条件。

3 求解方法

3.1 微分进化算法DE介绍

微分进化算法与遗传算法相似，同样包含交叉、进化、选择等过程。但与传统的优化方法相比，微分进化算法的区别在于：1）微分进化算法从整个种群开始搜索；2）微分进化算法是针对变量的，不对优化函数进行操作，也不对连续性作要求；3）微分进化算法摒弃了确定性的操作，采用概率方法。

夏冰一边往后门走，一边回头看，不想踢翻了一个花盆，花盆掉进水池里，激起一股水花，一声闷响在静夜里格外刺耳。“谁？”夏冰听得身后方向传来一声询问，心里一惊，立即矮在树影里，紧握手枪，浑身冒汗。过了好一会儿，并不见人，才小心地站起来，四处打量。

微分进化算法DE的变异、杂交和选择操作是基本操作，下面进行介绍。

3.2 数据初始化

设初始化种群 S = ｛ X , X ,… ,X ｝,X ∈Rn，第i个个

1 2N i体Xi= (xi,1, xi,2, … ,xi,n)，其中n为优化问题的解空间维数。一般个体向量 Xi的各个分量按下式产生：

式中,ijx ，,maxijx ，,minijx 分别为个体向量Xi的第j个分量以及第j个分量的上限和下限。

3.3 微分进化算法DE变异操作过程

微分进化算法的变异操作原理是，在种群中随机选择 2个个体，相减形成一个新的向量，再乘以一个变异因子，形成变异增量。变异操作可表示为：

3.4 微分进化算法DE交叉操作过程

交叉操作的关键在于，后代的第i个个体的第j个基因取决于变异得到的中间个体和当前个体其操作过程如下：

3.5 微分进化算法DE选择操作

DE算法的选择操作过程如下：

3.6 DE的控制参数

DE算法有4个控制参数: 种群数量Np，变异因子F，杂交因子CR，终止迭代次数C。一般来说，种群数量Np为5～10倍维度；变异因子F取值范围一般为[0.4,0.9]；杂交因子CR的取值区间为[0.3,0.8]。

3.7 控制参数的自适应调整

DE算法寻优的关键因素就是参数的选择。其中F和CR应该不小于某一特定值，防止出现早熟现象，但较大的F和CR可能导致局部最优解。然而，若F＞1，则算法的收敛速度会明显降低，收敛会更困难。因此，需要建立控制参数的自适应调整策略，使得算法具有更好的鲁棒性。

在本文的研究中，构造群体适应度方差来体现当前个体与最优点的分布关系，其计算公式如下

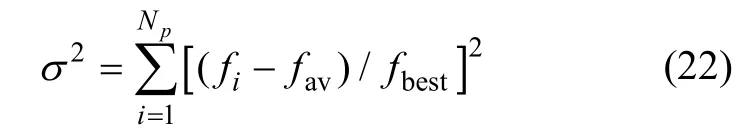
式中NP为种群数量；fi为第i个个体的适应度；fav为种群的平均适应度；fbest为群体最佳适应度。适应度方差的取值范围在[0，NP)之间，群体适应度方差2σ反映了种群的聚集程度。则DE算法的控制参数自适应调整策略为

3.8 微分进化算法改进（IDE算法）

为了解决DE算法可能出现的早熟问题，本文的改进算法采用解群转换方法进行改进操作。

对解群 Xi的第 j维分量按下式进行解群转换操作重新生成：

下面给出分散度的定义。当超过给定的分散度限制值时，进行解的转移以脱离局部最优点，否则继续保持原有搜索途径。公式如下：

式中 NP代表种群数量；n代表个体维数； ε1∈[ 0,1]、ε2∈ [ 0,1]分别代表设定的种群理想差异系数和相对于最优个体的理想差异系数；这里ηi,j为个体差异的指数，当ηi,j为0时表示第i代个体的第j维分量接近于最佳个体的第j维分量。如果种群多样性的程度因数u小于ε1时，将进行变异操作产生新的个体来摆脱局部最小而导致的早熟问题。

4 算例分析

算例系统考虑图 1的系统并进行适当简化。该系统包含主网等效电源、等效网络、WT、ES、以及负荷。设置仿真参数如下：WT的运行管理系数WTK 设为0.0096；ES的初始投资成本Ccost设为200 000元；b设为0.233 3；传输功率的上限 Pgrid,max设为 10；ES剩余电量最小值SOCmin设为20%；ES剩余电量最大值SOCmax设为80%；a设为0.007 1；c设为0.433 3。仿真当日的风电功率和负荷变化情况如图2所示，实时电价表见表1。

图2 风电和负荷变化情况Fig.2 Wind power and load changes

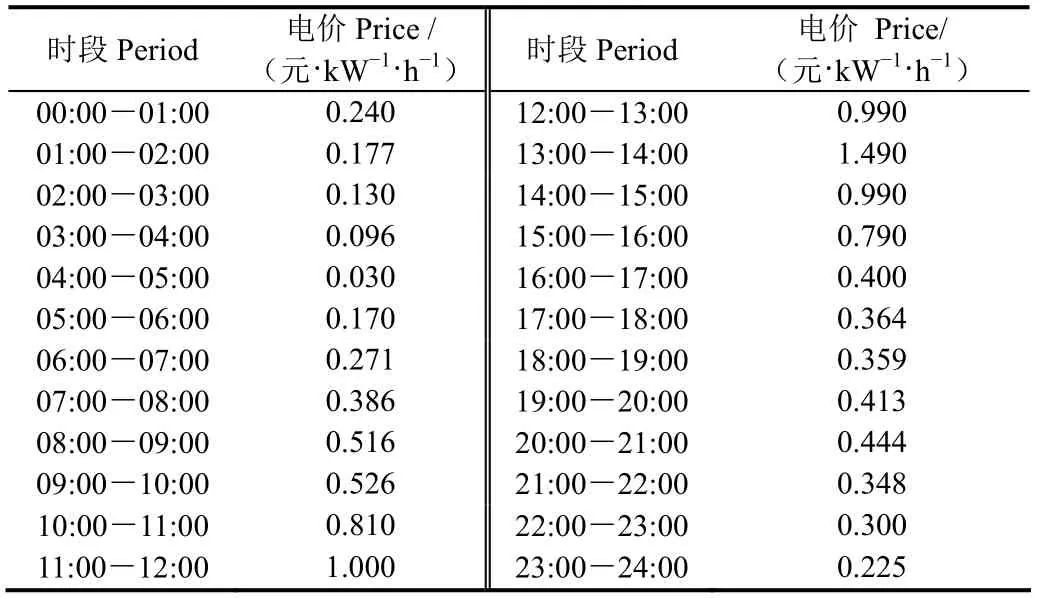
表1 实时电价Table 1 Real time price

4.1 算法的比较

本研究采用Matlab语言对改进微分进化算法（IDE）进行编程计算，同时跟基本微分进化算法（DE）计算结果进行比较分析。基本微分进化算法（DE）中种群数量Np设为30，终止迭代次数C设为100，变异因子F设为0.5，交叉因数CR设为0.4。改进微分进化算法(IDE)中种群数量NP设为30，终止迭代次数C设为100，变异因子的上下限Fmax，Fmin分别设为0.9，0.4，交叉因子的上下限CRmax，CRmin分别设为0.8，0.3，解群转换操作系数1ε和2ε分别设为0.6，0.01。

从图3、图4中可以看出：微分进化算法最佳适应度进化曲线呈阶梯状，运算到20代左右时逐步接近最优解；在15代之前，由于采用了控制参数的自适应调整措施，IDE算法明显比DE算法收敛速度快。在15代之后，出现局部最小而导致的早熟问题时，IDE进行解群转换操作。从适应度方差曲线可以看出，DE算法种群适应方差曲线由大变小，最后变成0，说明种群收敛到了个体；而IDE算法种群适应方差曲线在20代后不断波动，证明了该算法有利于维持种群多样性，有效地避免收敛到局部最优。

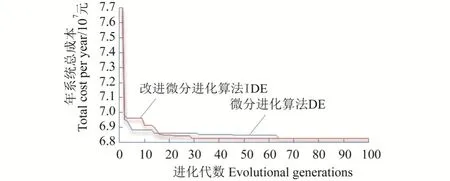
图3 微分进化DE算法和改进微分进化IDE算法进化迭代过程Fig.3 Evolutionary iterative process of differential evolution (DE)algorithm and improved differential evolution algorithm (IDE)

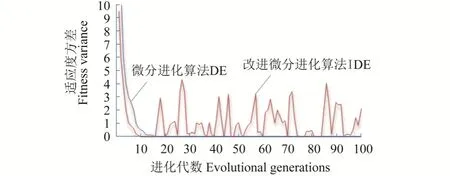
图4 种群适应方差动态演化曲线Fig.4 Population adaptation variance dynamic evolution curve

4.2 不同算法调度结果比较

为了说明优化调度算法的优势，选择遗传算法（genetic algorithm，GA）进行比较。将调度周期N取为24 h，间隔T=1 h，仿真计算结果如表2所示，储能及功率交换情况如图5所示。

表2 两种方案经济调度费用计算结果Table 2 Calculating results of economic dispatching costs of two schemes

图5 计算结果Fig.5 Calculating results

由图5可知，在整个日调度周期内，相比GA方案，IDE方案中的ES容量波动较小，变化更加平稳，SOC的最大值和最小值分别为80%和39%（GA方案分别为80%，22%），ES寿命等效成本IDE方案更低，差额为6476元。

由表1可知，09:00―16:00时为电价高峰期，此时IDE方案ES主要采取放电的策略，获得不错的售电收益；而GA方案中，在01:00―05:00时ES耗费的能量较多，虽然取得部分售电收益，但在电价高峰时段却由于ES容量不足一直充电，至13:00时才开始放电，反而浪费黄金时段的售电收益。

15:00―24:00时是用电高峰期，此时ES容量不足于满足全部负荷用电，2种方案都要从外网购电，但由于IDE方案中计及了ES的寿命成本，导致在该时段购电成本较高，而GA方案ES充分放电，因此购电成本要低于IDE方案。

综合以上分析，IDE方案的调度成本要比GA方案少9325元，IDE方案更优，在很大程度上提高了经济效益和ES寿命。

4.3 不同场景下调度结果比较

为了比较各类调度目标对调度结果的影响，设定 3种情景：Case 1：该场景不引入需求响应；Case 2：该场景不引入储能；Case 3：综合场景，即本文策略。各场景比较结果如表3所示。

从负荷角度来看，需求响应较好地降低了最大负荷和最小负荷的差距，负荷差从5.15 kW降低到3.91 kW，实现了削峰填谷，但并不能减少总负荷的大小。较小的负荷峰谷差也为储能的健康充放电提供了条件，有效地降低了储能的工作强度，如Case 1和Case 3所示。

从储能的角度来看，有无储能对园区的调度策略影响很大，Case 2中没有储能的状态下，造成电能供给不足，园区的购电成本大大增加了22 526元，导致经济效益和环境效益大大下降。

综合来看，良好的负荷侧需求响应和储能健康充放电是改善园区综合效益的基础，储能充放电策略是园区优化运行的关键。因此，本文所提出的调度优化策略能够有效改善运行设备运行状态，经济效益显著。

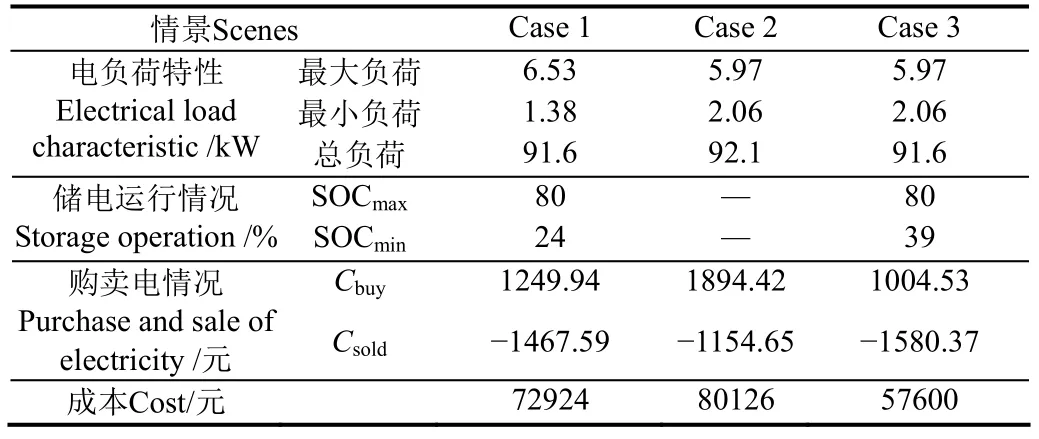
表3 各种场景计算结果Table 3 Calculating results of various scene

5 结论

在考虑实时电价、储能系统（ES）寿命的基础上，建立了风/储系统经济优化运行模型，采用改进微分进化算法进行计算，制定改进的经济调度策略。

仿真结果表明，日调度周期内，改进微分进化算法(IDE)方案中的 ES容量波动较小，变化更加平稳，SOC的最大值和最小值分别为 80%和 39%，相比遗传算法（GA），ES寿命等效成本IDE方案更低，差额为6 476元；综合各个时段的购电成本、售电收益、寿命成本等因素，IDE方案的调度成本要比GA方案少9 325元。

从负荷角度来看，需求响应将负荷差从5.15 kW降低到3.91 kW，实现了削峰填谷。从储能的角度来看，有无储能对园区的调度策略影响很大，无储能的状态下，造成电能供给不足，成本增加22 526元，导致经济效益和环境效益下降。基于 IDE算法的改进经济调度策略能够更好地平衡各类成本，提高系统经济效益和ES寿命。

在本文研究的基础上，未来还可有以下研究方向：1）本文设置的成本函数较为简单，实际情况可能更加复杂，可以进行深入的研究；2）在经济调度的目标函数中，可以加入环境成本，使之更加完善。