深水养殖网箱浮架变形模拟及结构改进设计

黄小华，刘海阳，胡 昱，陶启友，王绍敏，袁太平

(中国水产科学研究院南海水产研究所，广东省网箱工程技术研究中心，农业部外海渔业开发重点实验室，广州 510300)

0 引 言

当前，中国临海重工业、滨海旅游业发展迅速，部分近岸海域污染严重，近海养殖业发展空间进一步压缩，海洋养殖向离岸深水发展已成业界普遍共识。深水网箱通常设置于较深海域，具有养殖水产品品质好、产量高、效益大的显著优势，已成为中国深水养殖拓展海洋养殖空间的重要设施装备[1-4]。但由于深水海域海况复杂，深水网箱系统必须具备足够的安全可靠性来抵抗大浪强流的冲击，以降低养殖风险和保障养殖效益。作为网箱系统的重要组成部分，浮架系统在网箱抗风浪性能中起到至关重要的作用[5]。国内外已有众多学者采用计算机模拟方法开展了深水网箱水动力特性研究，但绝大多数研究均未考虑网箱浮架的实际变形情况，往往将浮架假设为刚体[6-11]。实践表明，由高密度聚乙烯（high density polyethylene，HDPE）材料制作的浮架在波浪流冲击下具有明显的变形，且规格越大的深水网箱，其浮架变形越大[12]。Huang等[12]通过建立数值模型模拟分析了纯波条件下浮管的弹性变形，确定了浮管变形最大位置，并对网箱模型的正确性及有效性进行了验证。此外，物理模型试验作为一种有效的方法也被广泛应用于网箱动力学研究中，主要涉及网箱浮架运动[13-16]、网衣运动变形[17-23]、锚泊受力等[24-27]。但由于小比例尺网箱模型试验在满足几何相似的条件下无法满足网箱浮架的刚度相似，使得开展波浪流网箱试验时，由于浮架变形太小而不容易观测，在试验验中网箱浮架基本上为一个未变形的刚体，尤其在测试水流作用下网衣变形时，通常将浮架完全固定住[17-18]。近年来，随着网箱大型化发展，浮架变形问题不容忽视，过大变形甚至会导致浮架失效破坏，从而造成重大经济损失。国内外已有部分学者采用数值模拟方法，开展了网箱浮管的动态变形响应[28]、疲劳分析[29]、锚绳张力[30]以及网箱护栏的力学性能分析[31]。如Li等[28]采用Abaqus软件将浮架简化为一根单浮管，基于杆单元和梁单元建立的网箱模型，分别模拟分析了浮管及网衣的运动响应，计算获得了不同流速条件下的网衣容积损失率。

抽穗扬花期要求空气湿度为70%～80%，土壤湿度占田间持水量的70%～80%，并要求有充足的光照。土壤湿度>85%或<60%均有不利影响。

该研究是在文献[12]的基础上，基于有限元方法建立整体网箱系统数值模型，并对波流联合作用下网箱系统模型的准确性进行了验证。在此基础上，以中国南海区常用规格80 m周长的HDPE圆形网箱为研究对象，开展波浪流组合工况下浮架变形模拟研究，评估了网箱系统浮架极限承载力，科学提出了一种能够有效增强网箱浮架结构安全的技术措施，旨在有效降低网箱结构在台风冲击下发生的失效破坏风险。

另外，在卖粮的过程中，注意水分测试的骗局。玉米水分达标后才能卖，于是，有的人就做起了水分测试仪的文章，他们通过一些手段将仪器改变，不管怎么测，粮食都是不合格的，这样就可以压低粮食收购价。

1 数值模型

基于专业水动力分析软件Orcaflex[32-33]，建立深水网箱系统数值计算模型，采用有限元法将浮架离散成系列线单元及质点，利用线单元模拟网箱系统各部件，包括浮架、网衣及锚绳，质点位于线单元的两端。质点分为2种：六自由度质点和三自由度质点。对于网箱浮架，采用六自由度质点来传递弯矩；而对于柔性网衣及锚绳构件，线单元的两端为三自由度质点，设置为自由旋转不承受弯矩。将每个线单元受到的力及力矩，包括重力、浮力、波浪力、张力、剪力及弯矩等，集中到线单元两端的质点上，建立每个质点的运动方程见式（1）[32]：

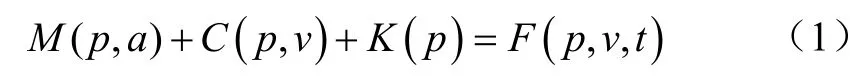
为了进一步验证整体网箱系统有限元计算模型的正确性和有效性，针对Li等[28]波流组合条件下单浮管网箱系统的动态变形情况进行了数值模拟，并将计算结果与文献中数据进行比较，具体计算参数及网箱布置详见参考文献[28]，波流组合条件设置为：波高5 m、周期8 s、流速为0.6 m/s，波浪为规则波。图3为波流作用下浮管最左端点水平方向和竖直方向位移的时间历程线。从图中可以看出，基于本研究建立的有限元模型的计算结果与Li等[28]的研究结果均比较吻合，位移最大相对误差在5%以内，表明本研究建立的有限元模型适用于模拟波流组合条件下网箱系统的动力响应。

1.1 结构荷载

网箱的结构荷载来自于各部件，对于 HDPE材料的浮架主浮管，波浪流作用下其结构荷载包括张力、剪力及弯矩；对于网衣及锚绳部件，因弯曲刚度很小可以设置为零，其结构荷载主要为结构单元的张力。线单元张力的计算表达式为[32]

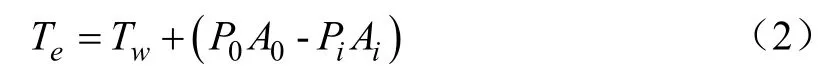
域间二维路由器建立协议连接时，会向对端路由器其发送携带二维路由标识的OPEN报文。如果对端路由器支持域间二维路由则回复携带有相同标识的OPEN报文，如果对端路由器不支持二维路由即无法识别标识信息，则返回常规的OPEN报文。发起连接的域间二维路由器会根据返回的OPEN报文是否携带特定标识来识别和记录对端路由器是否支持二维路由，将来二维路由相关信息只会发给建立连接的二维路由器，而不会发给传统路由器。

式中Tw为管壁张力，kN，可根据式（3）计算得到。

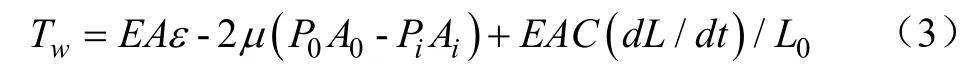
式中SZ为线单元轴向单位向量；M1和M2分别为线单元两端的弯矩，kN·m；L为线单元即时长度，m。

纳什均衡是博弈到达均衡时的一种状态。在这个状态下，博弈中任何参与者在其他参与者的策略既定的情况下，都无法通过改变当前策略来获得更好的支付或更高收益。如果∀si∈Si,πi(S*)≥

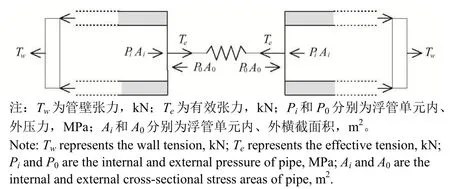
图1 浮管结构张力计算示意图Fig. 1 Sketch of tension and pressure forces of pipe structure

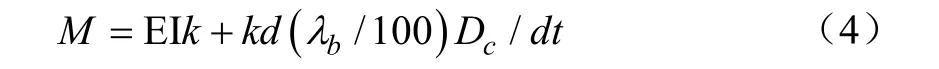
计算浮架结构线单元弯矩后，其剪力可根据下式相应得到[32]

式中 EI为线单元浮管的弯曲刚度，kN·m2；k为曲率，m-1；λb为目标弯曲阻尼占比，Dc为弯曲临界阻尼值等于L0(mEIL0)1/2，kN·m2；在线单元的两端质点具有弯矩 M1和 M2，kN·m。

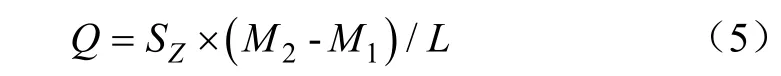
浮架结构线单元承受的弯矩可以表示为[32]

师：嗯，你提出了一个很有价值的问题，就是“角“有大小之别，那角的大小用什么来度量？这节课，我们一起来学习角的度量。板书课题：角的度量

式中EA为线单元轴向刚度，kN；ε是轴向应变，Pi和P0分别为浮管单元内、外压力，MPa；Ai和 A0分别为浮管单元内、外横截面积（见图 1），m2；C为阻尼系数，μ为泊松比，dL/dt是线单元长度增长率，L0为线单元初始长度，m。对于网衣和锚绳部件，P0A0等于PiAi。

根据地勘报告，该场区土层中，第1层耕填土含潜水，第5层粉土中含弱承压水，其余各层均为微透水、弱透水或不透水层。场区稳定水位在2.40～2.62 m(黄海高程)之间，随季节动态变化，夏高冬低，历史最高洪水位达到3.40 m。在该工程施工期间，由于基坑的周围设计了密排的混凝土搅拌桩作为止水帷幕，因此，地下水的主要来源是大气降水，施工结束后，雨水通过周围的回填土渗透到地下。综合以上分析，假定该工程的抗浮水位设计值为3.0 m。

1.2 环境荷载

网箱各部件包括浮架、网衣、锚绳的结构线单元的水动力荷载均采用Morison方程计算，包括速度力及惯性力两部分[34]

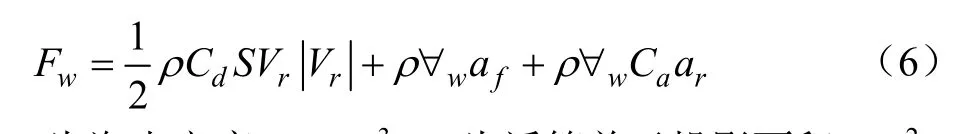
式中ρ为海水密度，kg/m3；S为浮管单元投影面积，m2；Vr为水质点与线单元构件的相对速度，m/s；w∀为线单元构件排开水的体积，m3；af为水质点加速度，ar为相对加速度，m/s2；Cd和Ca分别为速度力系数和惯性力系数。

在作者此前的研究中[12]，已分别采用集中荷载下单圆管变形和规则波作用下单圆管的运动变形 2个算例的研究数据，对数值模型的计算结果进行了比较验证，结果显示数据吻合很好，验证了模型的合理性，具体介绍详见文献[12]。

当网箱浮架在波浪作用影响下，其结构的入水深度会随着波浪运动时刻发生变化，浮架结构的浮力需时刻根据每一个线单元的入水比例重新计算得到（见图 2），见式（7）。

式中Pw为入水比例，∀B为线单元体积，m3。

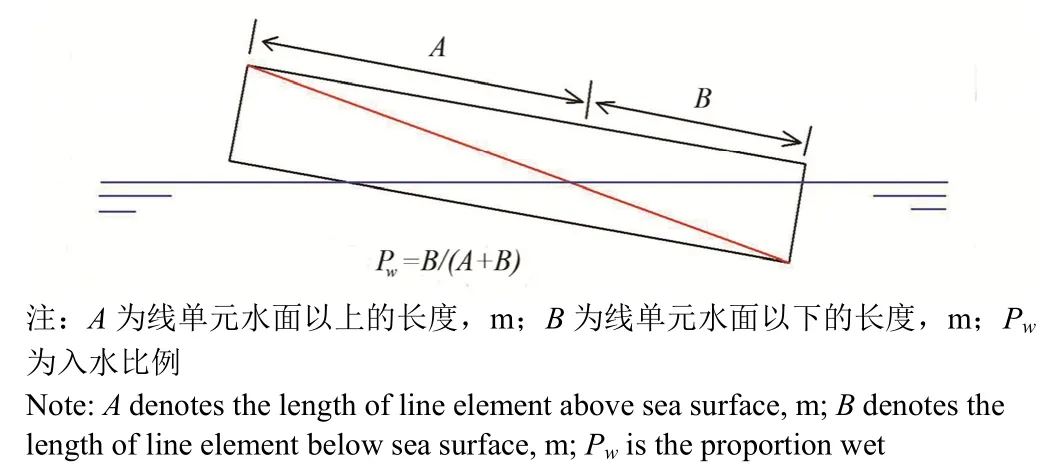
图2 浮架结构线单元浮力计算示意图Fig. 2 Proportion wet for surface-piercing segment

2 模型验证

借用国标件——针阀式注油杯[3]，容量为16cm3，通过螺纹连接安装在壳体上。使用时，打开针阀开关，容器内的消毒液即滴入剪叶器壳体内，通过高速旋转的切刀打成雾状，实现对壳体内所有零件的消毒，防止污染烟苗。

式中M(p, a)是惯性荷载，C(p, v)是阻尼荷载，K(p)是刚性荷载，F(p, v, t)是外力荷载，kN；p是位置，m；, v 是速度，m/s；a是加速度，m/s2。

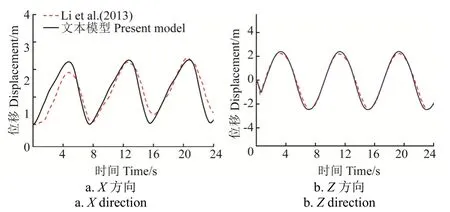
图3 浮架运动位移比较Fig. 3 Comparison of displacement for floating collar

3 网箱系统布置及结构参数

针对中国南海区常用规格周长80m的HDPE圆形网箱，开展波浪流组合工况下浮架的受力变形分析，评估网箱系统中浮架的极限承载力。如图 4所示，网箱浮架简化为2根平行的内外浮管，内外浮管之间设有40个连接件，相邻2个连接件间隔2 m。浮架采用8点系泊方式。网衣为圆台形状，在网衣底端装配沉子作为配重。波浪传播方向沿 X轴正方向。网箱系统各部件尺寸及相关参数值见表1。

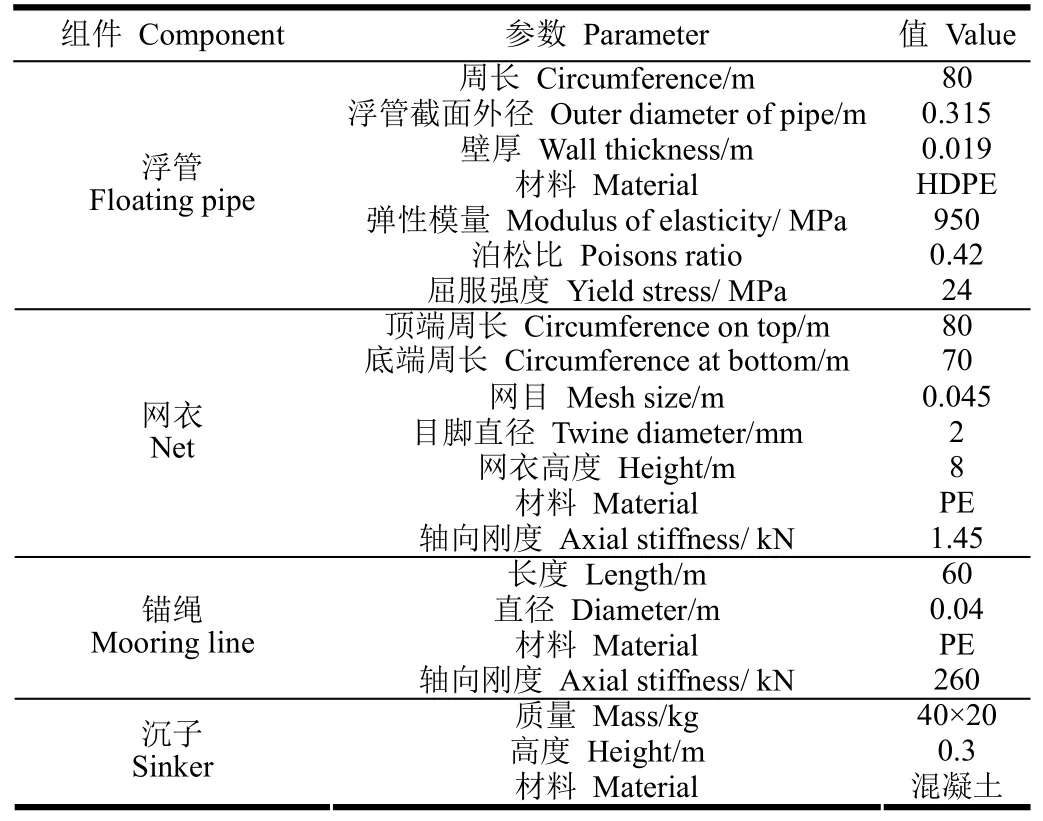
表1 网箱各部件参数Table 1 Parameters of each componet of net cage for calculations

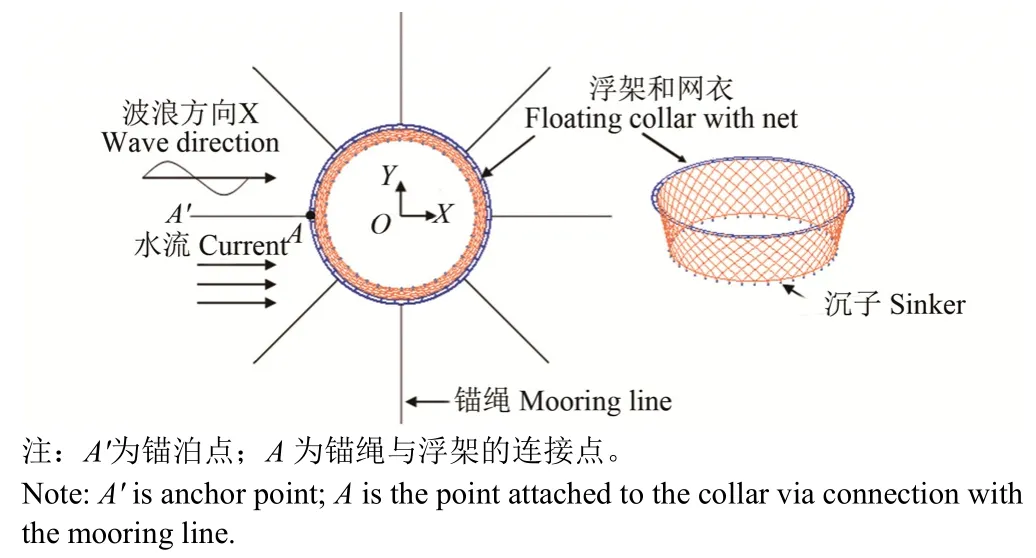
图4 整体网箱系统布置图Fig.4 Configuration of floating net cage

4 网箱浮架变形分析

在外海大浪强流的冲击下，网箱系统的受力变形加大，对网箱结构安全性能构成威胁。采用von Mises应变及应力来反映浮架不同位置处的变形情况，其计算表达式分别见式（8）、式（9）[32]。

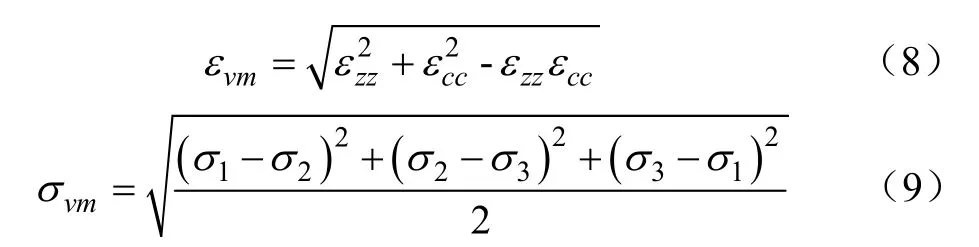
式中 εzz为轴向应变，εcc是环向应变，%；σ1, σ2, σ3分别是3个方向的主应力，MPa。

计算过程中波浪为规则波：波高5、6、7m，周期9、11、13 s；流速设为0.6、1.0、1.5 m/s。根据本文作者此前研究结果显示，当锚绳布置方向与波浪流方向相同时的浮架系泊点位置处变形最大[12]，为此选取图 4中的 A点位置作为分析浮架变形的依据。

图 5为大浪强流冲击下网箱系统的浮架变形响应。考虑到篇幅有限，未给出所有27种波流工况下的计算结果，这里仅列出两种波况和不同流速组合条件下的浮架变形模拟结果。比较得知，浮架的变形随着波高及流速的增大而增大，但随着波浪周期的增加变化很小，表明波浪周期对浮架变形的影响很小。在27种波浪流组合工况下，其中波高5m、周期13s、流速0.6 m/s条件下的浮架变形最小，最大应变值为1.14%（见图5a）；而波高7m、周期9s、流速1.5m/s条件下浮架变形最大，最大应变值为2.47%（见图5b）。参照弹性范围内von Mises应力和应变的线性关系曲线，波高7 m、周期9 s、流速1.5 m/s条件下的最大应力值为23.47MPa。根据浮管HDPE材料的屈服强度为24MPa[35]（见表1），则表明网箱在波高7m、周期9s、流速1.5m/s条件下，浮架变形接近弹性变形的临界值，浮架面临屈服破坏的风险很大。为此，需要考虑相应技术措施来减小浮架的变形，以避免浮架塑性破坏的发生。

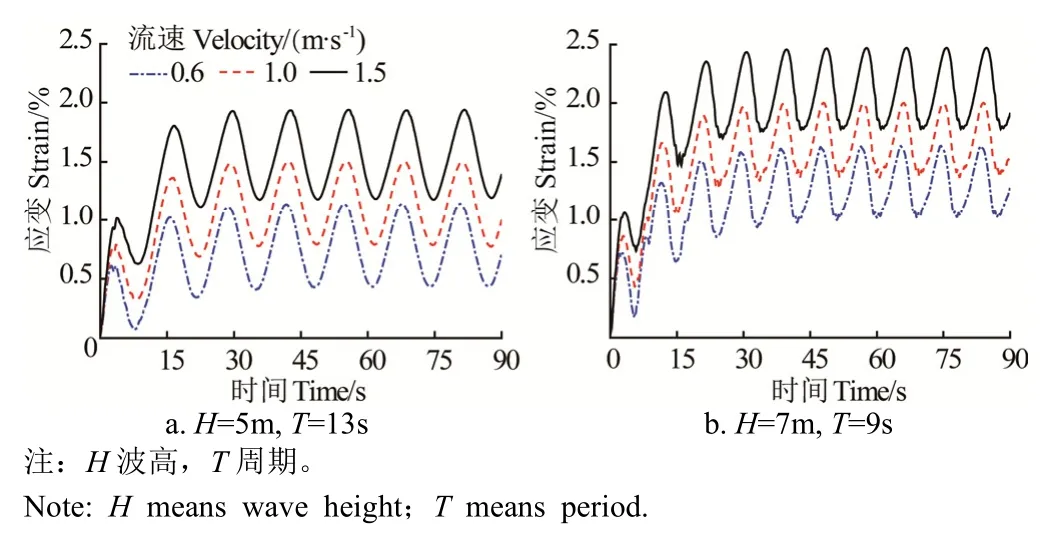
图5 整体网箱系统在规则波和水流组合工况下浮架A点位置处应变历时曲线Fig.5 Time-series of von Mises strain at point A under conditions of regular waves and current of floating net cage

5 浮架结构改进

由于浮架较大受力变形发生在锚绳系泊处，台风浪条件下锚泊系统受力过大导致浮架系泊处因弯曲变形严重，致使浮架坍塌破坏现象时有发生[5]，因此对锚绳与浮架连接处进行加固显得尤为重要。根据上述研究结果，由于在波高7m、周期9s、流速1.5 m/s条件下浮架发生屈服破坏的风险极大，为此考虑在浮架每个锚绳系泊处增加一个套管（见图 6），套管长度 500 mm，截面直径355 mm，壁厚15mm。浮架上共有8个锚绳系泊点，因此需要加设8个套管，套管之间长度为10m。设定的大浪强流条件与第4部分相同，因在设定的3种波浪周期条件中，波浪周期9s时的浮架变形稍大，故波浪周期统一设定为9s。

表 2为各种波浪流组合工况下有、无套管分别对浮架变形的影响比较，浮架变形仍选用A点的最大应变值来反映。由结果比较发现，在锚绳系泊处增设套管可以较大地减小浮架变形，如设有套管时在波高 7m、流速1.5m/s的波流组合工况下，最大应变值为1.34%，大大小于浮架无套管的情况，降低幅度达45.7%。说明在浮管系泊点处增加套管可以大大增强恶劣海况下网箱系统抵御自然风险的能力。图7为浮架A点所受锚绳张力与应变的关系曲线图，图中实线代表无套管的计算结果，虚线代表增设套管的计算结果。图中显示，无套管时的应变值范围为 1.27%～1.77%、锚绳张力变化范围为 31kN～45.6kN；增设套管后的应变值范围变为0.61%～0.94%、锚绳张力范围为32kN～46.8kN。说明增加套管对减少浮架应变值明显，而对锚绳张力几乎没有影响。在波高6m、周期9s、流速1.0m/s的相同波流工况下，两者的锚绳力峰值同约为46kN，说明浮架增设套管不会对锚绳张力有影响。

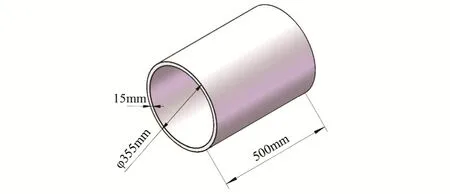
图6 浮架套管模型示意图Fig. 6 Sketch of casing pipe model

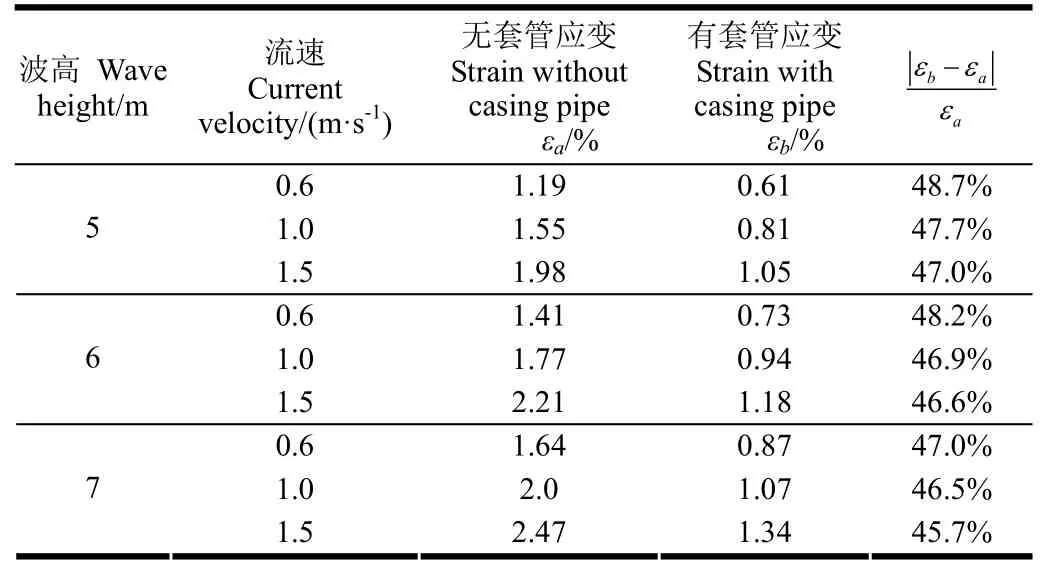
表2 有、无套管时浮架A点位置处最大应变值比较Table 2 Comparison of maximum von Mises strain at point A for cage with and without casing pipes

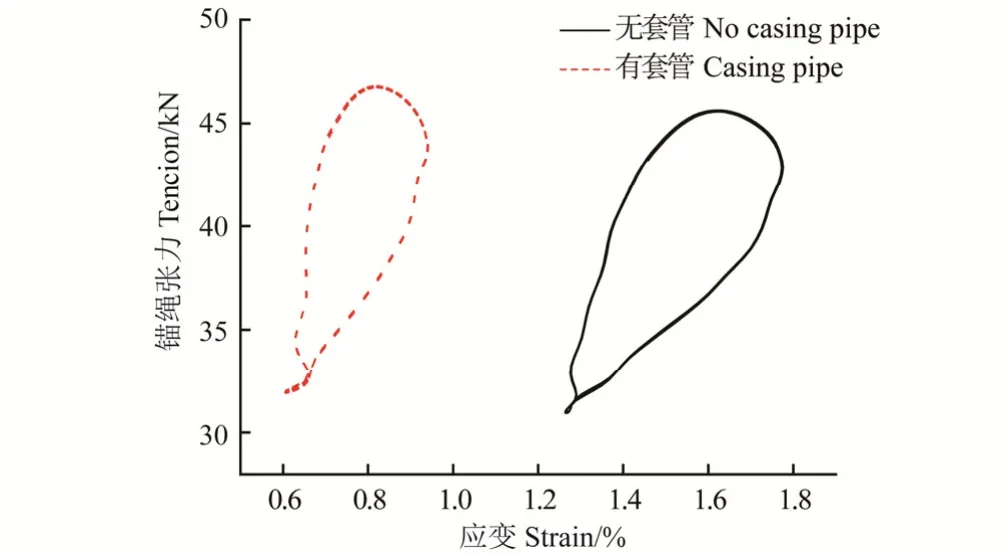
图7 锚绳张力与浮架变形的关系曲线（H=6m, T=9s, V=1.0m/s）Fig.7 Relationship between mooring line tension and strain under waves and current where wave height H = 6 m, wave period T = 9 s, and current velocity V = 1.0 m/s

6 结论

本文对大浪强流条件下深水网箱浮架系统的动力变形进行了模拟分析，并对浮架结构进行了改进研究，得到如下几点结论：

在每次迭代时,都采用归一化算法w←w/‖w‖,利用施密特正交化过程,使第p个特征向量与其他特征向量不相关，即

1）基于有限元法建立了波流作用下的网箱系统动力变形数值模型，并通过算例对模型的有效性及准确性进行了验证，浮架的最大位移相对误差在5%以内。

2）通过对80m周长的HDPE圆形网箱在不同波流组合工况下的浮架变形模拟结果的比较分析，发现浮架变形随着波高或流速的增加而增大，而受波浪周期的影响很小。在波高7m、周期9s、流速1.5m/s的波流组合条件下，浮架最大应变值为2.47%，浮架发生局部屈服破坏的风险极大。

3）为降低高海况下浮架局部屈服破坏风险，对浮架结构进行了改进，模拟结果表明，在浮架锚绳系泊处增设套管可以有效减小浮架变形，相比无套管情况，浮架最大应变值减小幅度达 43%，大大增强了恶劣海况下网箱系统抵御自然风险的能力。