PCA与随机森林相结合筛选高信息量SNP位点——应用于羊的品种鉴别

刘月丽，覃锡忠，贺三刚，李文蓉，王 悦，贾振红，刘明军

LIU Yueli1,QIN Xizhong1,HE Sangang2,LI Wenrong2,WANG Yue1,JIAZhenhong1,LIU Mingjun2

1.新疆大学 信息科学与工程学院，乌鲁木齐 830046

2.新疆畜牧科学院 生物技术研究所，农业部草食家畜繁育生物技术重点开放实验室，新疆维吾尔自治区动物生物技术重点实验室，乌鲁木齐 830046

1.College of Information Science and Engineering,Xinjiang University,Urumqi 830046,China

2.The Key Laboratory of Livestock Reproduction&Breed Biotechnology of MOA,The Key Laboratory of Animal Biotechnology of Xinjiang,Xinjiang Academy of Biotechnological Center,Urumqi 830046,China

1 引言

生物品种鉴别有着广泛和重要的应用价值。品种鉴别促进了对遗传信息的有效管理[1]；为育种策略的制定与实施奠定良好基础[2]；为生物品牌产品的认证提供了有效信息[3]；更为解决食品安全问题开辟了新途径[4]。在以往品种鉴别研究中少有涉及羊的种类鉴别，而我国有着饲养羊群的悠久历史，拥有丰富的羊群遗传资源，据《中国畜禽遗传资源志·羊志》记载的我国地方羊品种就达42个[5]，约占世界羊品种的5%[1]。本文将SNP位点应用于羊的品种分类。

在早期的品种鉴别研究中，利用微卫星和ALFP标记进行动物鉴别[6-7]。随着基因芯片技术的飞速发展，SNP位点渐渐用于动物品种及其副产品的鉴别中。与微卫星标记相比SNP位点的优势在于：基因分型错误率低，在基因组中分布广泛，检测速度快，易于标准化[8]。品种鉴别是对基因数据实际应用的一次探索性研究。已有的相关研究中将遗传信息与基本的数学统计方法相结合用于品种鉴别：Pfaff等人利用δ方法[9]，以两个物种间的等位基因频率绝对差为判别标准进行分类；Weir等人利用 Wright’s FST方法[10]，依赖于预先定义的两个物种间的等位基因频率的差异最大化进行判别。然而δ和Wright’s FST只可以用于两个种群的判别，并且没有清晰的统计特性定义。为解决两个品种以上的判别，Rosenberg等人[11]提出了一种相关性衡量的方法，使用互信息（In）描述相关性，以此来表示不同品种的FST之间的关系。很明显，上述的传统方法都没有考虑到SNP数据的高维小样本的特点[12]（本文中维度就达到了近50000），且都需要计算等位基因频率，大大增加了计算复杂度和运算量。为此，Paschou等人[13]提出利用PCA提取SNP位点的方法。

PCA虽然可以有效地降低样本维数，但是对于品种鉴别来说SNP位点个数还是过多。而且PCA对非线性数据的分类效果并不好，也无法评估所选SNP位点的重要程度。为了有效解决这些问题，本文将PCA和随机森林相结合提取高信息量的SNP位点。随机森林有以下优点，可以利用数据之间相互依赖的信息，构建多元分类规则；在每个类别边界上有很好的非线性；提供了变量重要性的衡量方法。目前还未被用于品种鉴别的高信息量SNP位点的识别中。

为验证方法的可行性，本文针对6种绵羊llumina OvineSNP50的SNP数（AustralianPollDorset羊、AustralianSuffolk羊、MilkLacaune羊、Soay羊、德国肉用美利奴羊GMS、哈萨克羊KSK），先利用PCA进行降维，去除冗余SNP位点，得到一个特征SNP子集。再利用随机森林评估这些SNP位点的重要性，并选出重要性排名靠前的SNP位点用于分类。最后，通过分类测试实验，验证了本文方法能够利用少量高信息量的SNP将未知品种的羊正确分类。

2 PCA和随机森林相结合提取SNP位点

PCA和随机森林相结合筛选高信息量SNP位点算法流程如图1。

2.1 SNP数据集与预处理

先将SNP基因型数据进行编码，但是SNP位点采样时不可避免地存在缺失值，因此对整个数据集进行缺失值插补。插补概率遵循哈温伯格平衡定律，使得SNP位点在不同品种中分布更加均衡，不会引入人为的偏倚。最后将数据分为训练集和测试集。

2.2 基于PCA的SNP位点提取

PCA是一种线性降维技术，可以从过于“丰富”的数据信息中捕获最重要的元素和结构。在遗传学中每个个体可以提取出来数以万记的SNP位点。由于维数过高，需要先将这些数据进行编码，再利用PCA和奇异值分解（Singular Value Decomposition，SVD）提取主SNP位点。

将编码后的SNP数据看成矩阵Xm×n，其中m为样本个数，n为SNP位点数目；再用SVD对矩阵X进行运算，返回m个正交向量ui,n个正交向量vi以及m个非负的奇异值δi。矩阵X表示成如下形式：

其中，左奇异向量ui与X的列（SNP位点）有关，是X矩阵列向量的线性组合，称作特征SNP[14]。可以保留少数特征SNP，达到降维的目的。再利用所选择的特征SNP表示所有样本，进行下一步的数据分析（如聚类或者分类）。

然而特征SNP是一种数学抽象，并不代表实际的SNP位点。Drineas等人[14-16]证明，由特征SNP张成的子空间所得到的奇异向量，可以近似表示矩阵X中的奇异向量。基于这一理论，所选出来的特征SNP就和实际SNP位点有关。假设有k个主成分，因此有k个特征SNP，则原始矩阵的列可以用前k个特征SNP张成的子空间中的列近似表示，如下式：

式中，表示第j个元素的第i个右奇异向量。X第j列由所有左奇异向量和其相应的奇异值组成，其中δiui是这个线性组合的系数。

图1 PCA与随机森林相结合的算法流程图

最后，利用对X矩阵的列进行评分，见式（3），选出最大的列组成特征SNP子集。

Drineas等人[15-16]证明，从X矩阵中，每次以概率pj独立随机选取j列，则被选择的这些列的前k个左奇异向量和原始矩阵的前k个左奇异向量十分接近。在实际应用中，选择pj值最大的列就可以达到很好的效果。

2.3 用于分类的随机森林算法

在实际应用中经过PCA预选后的SNP位点数目仍然很多，无法评估所选SNP位点的重要程度。因此需要建立一个规则，将样本分配到对应的品种中。出于这些目的本文利用随机森林进行分类。

随机森林是一种集成分类器[17]，在建模时有两个重要参数。一个是随机森林中决策树的数目，另一个是树节点预选变量的个数。第一个参数决定了整片随机森林的规模，第二个参数决定了单棵决策树的情况。算法流程如图2所示。图中每个节点都基于单一特征进行分类，每个分支的结束为终端节点。终端节点根据决策树的路径对样本的类别进行预测。终端节点的颜色表示预测的类别。对于样本的最终预测结果是基于所有的决策树的预测结果。

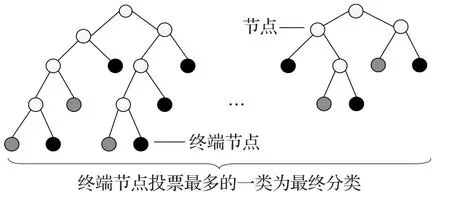
图2 随机森林的流程图（显示两棵树的细节）

随机森林中每棵决策树的训练集都是从原始训练集中抽取m个样本，每个样本的容量和原始训练集是一样的。这种方法叫作自助抽样法（Bootstrap Sampling）。这样每次有30%～40%的数据没被抽到，这些数据对于每棵树来说就是“Out-of-Bag（OOB）”数据。在随机森林的生成过程中利用这些数据在内部进行评估，可以得到相应的OOB错误率[18]，因此本文利用OOB错误率来评估随机森林的分类效果。如果OOB错误率为0，就表明每个样本都被正确分类了。

2.4 位点重要性评价准则

随机森林中每棵树的节点上，随机抽取d个特征用于二分类，并且d＜＜D,D是原始数据集中特征值的个数。父节点np可以根据Gini指数来划分子节点nl和nr。节点n的Gini指数可以用式（4）表示：

其中，pc代表在节点n处样本属于c类的相对概率。为实现最佳的二分类，两个子节点之间的Gini指数差值要取最大，Gini指数差值计算见式（5）：

其中，pl和pr分别表示np分裂为子节点nl和nr的比例值。

Gini指数可以评价的重要程度。还有一种衡量标准——平均精度下降（Mean Accuracy Decrease），可以作为节点分裂的标准，同时也可以评价用于分类的变量的重要程度。

3 实验及结果分析

3.1 SNP数据集与预处理

本文SNP位点数据来自于6个品种的羊，共计696个样本，其中Australian Poll Dorset 108个，Australian Suffolk 109个，Milk Lacaune 103个，Soay 109个，GMS 106个，KSK 161 个。Australian Poll Dorset、Australian Suffolk、Soay、Milk Lacaune来自于公开数据源ISGC（International Sheep Genomic Consortium），每个样本SNP位点数目46013个；而GMS和KSK由新疆畜牧科学院提供。共计26条常染色体，每个样本SNP位点数目54241个，包含了ISGC的所有位点；两类样本合并处理，用于实验的SNP位点个数共计46013个。然后进行数据预处理，过程如下：

（1）SNP位点编码。基因型AA编码为0；基因型AB编码为1；基因型BB编码为2，编码后的SNP位点数据构成矩阵Xm×n,m=696,n=46013。

（2）缺失值插补。利用0、1、2对整个数据集进行随即插补。

（3）训练集与测试集。从每个品种中随机抽取30%的样本组成测试集（Australian Poll Dorset 32只，Australian Suffolk 32只，MilkLacaune 30只，Soay 32只，GMS 31只，KSK 48只），用于测试最后的品种分配。训练集由余下的70%样本数据组成。

3.2 利用PCA选择高信息量的SNP子集

本文使用R语言3.3.0版本进行PCA计算。为了减少计算时间，分别按照每一条染色体进行计算，提高计算效率。每一个主成分所提取的信息量用方差来度量，其中某一个主成分方差的贡献就等于原指标相关矩阵相应的特征值δi，则第i个主成分的方差贡献率见式（6）：

Ti值越大，说明相应的主成分反映综合信息的能力越强。计算后的PCA方差贡献率见图3。

图3 所有SNP位点在前10个主成分上的方差贡献率

为保证准分类的准确性，最重要的是所选主成分是否涵盖了不同品种的差异，而不是累计方差贡献率的百分比。如图3所示，在PC2和PC3之间，主成分的方差贡献率值有大幅度的下降，因此保留前两个主成分，用于减少SNP位点的数目。再根据式（3）计算每个SNP标记的得分。利用得分对每条染色体上的SNP位点进行排名，选择每条染色体上排名前20的SNP位点，组成含有520个SNP位点的缩减集。

经过PCA计算后，SNP位点个数从46013减少到了520个。图4、图5展示了从520个SNP位点的协方差矩阵中分别提取出前两个和前3个主成分构成的空间。对于保留前3个主成分仅仅是以探索为目的，和Paschou等人[13]提出的基于PCA的甄选算法不同，本文对PCA结果绘图仅用于评价减少SNP的数量是否会丢失能够表达品种差异的相关信息。

图4 520个SNP位点的前两个主成分分析图

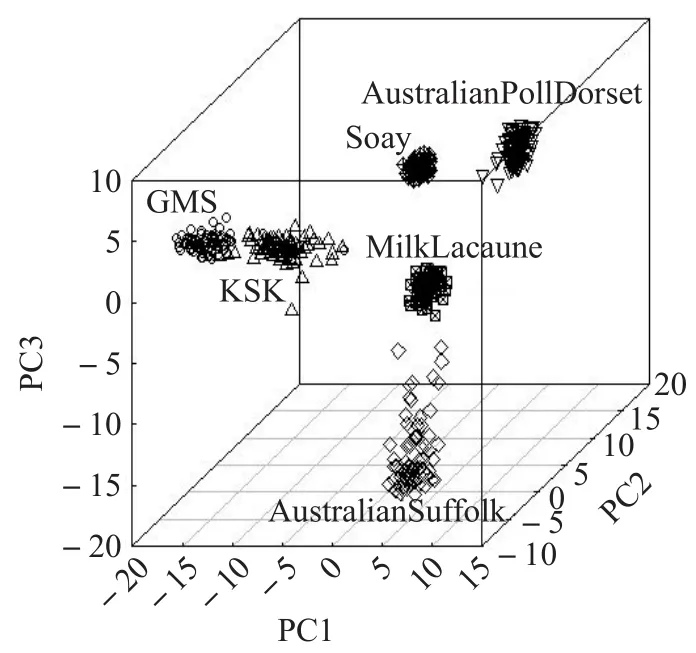
图5 520个SNP位点的前3个主成分分析图

由图4可以看出，在由前两个主成分组成的空间中GMS和KSK以及MilkLacaune之间有稍微的混叠，但是在三维空间图5中GMS和KSK以及MilkLacaune之间的混叠就消失了。PCA预先选择出的520个位点可以很好地表示不同品种之间的差异。

3.3 随机森林重要性评价及分类模型建立

利用随机森林，以预选出的520个SNP位点为基础，根据两种排名方式（Gini指数下降和平均精度下降），选择具有更大差异的SNP位点。根据实际应用保留排名前48和排名前96的SNP位点，用于最后的预测。对于这4种要求（两种排名方式×两种SNP集合），训练相应的随机森林模型，并计算对应的OOB错误率。最后，用测试集来测试最终的分类效果。

上节提到构建随机森林模型有两个重要参数，绘制图6（a）随机森林中决策树的个数与相关误差的关系，图6（b）树节点预选的变量个数与相关误差的关系，通过这两张图来选择参数值。

图6 随机森林参数与错误率之间的关系

由图6（a）可知：该模型的决策树数量在200以内时，模型误差会出现较大的波动。当决策树数量大于200后，模型逐渐趋于稳定，但还是有少许波动。通过观察发现在决策树数量为600时该模型的错误率最低，因此选择500为随机森林中决策树的数量。

由图6（b）可知：该模型在5之前错误率较高，在Mtry=6处错误率最低，之后错误率又有升高，因此每棵树节点预选变量的个数设置为6。

分别按照Gini指数下降和平均精度下降选出的SNP位点有一定的重叠。排名前48的SNP中有35个相同，排名前96的里面有68个相同。在Boulesteix等人[19]的研究中提出，基于Gini指数的排名靠前的位点的MAF（最小等位基因频率）值都较大。这也体现了本文分析方法的特性：剔除了基因频率较小的SNP位点。这样，实验中筛选出的SNP位点就能够捕捉到每个品种的普遍特性，也就是说所选出的SNP位点对于这几个品种来说具有较好的普适性。48个SNP位点的Gini指数如图7所示，可以明显看出不同的SNP位点对于分类的贡献不同，更利于对贡献较大的SNP位点进一步研究。

图7 48个SNP位点的Gini指数值

基于Gini指数选出的两种SNP集合的位点分布情况如图8所示。由图可知，在10号染色体上两种SNP集合（48和96）都有较多的SNP位点被选中（48中有6个，96中也有6个）。在96个SNP中，被选中位点最多的是1号染色体，有8个SNP位点。在48个SNP中有7个染色体上没有被选中的位点，分别是4、7、8、9、14、18、21号染色体。并且在96面板中，任何一条染色体上被选中的SNP位点个数都没有达到20个。说明本文选择出了每条染色体上最具代表性的SNP位点，也说明PCA预选出来的每条染色体上排名前20的SNP位点，是可以捕获到高信息量的SNP位点（用于品种分类）。

图8 被选中的SNP位点在每个染色体上的分布情况

3.4 随机森林的分类结果评价

为验证PCA可预选SNP位点，随机森林可以进一步减少用于分类的SNP位点个数并达到较好的准确率。基于4种数据集分别随机抽取48和96个SNP位点对随机森林的分类结果进行测试，结果见表1。

表1 利用随机森林的分类结果

方式1：从46013个SNP位点中随机抽取48个和96个SNP位点，然后用训练好的随机森林模型进行分类。OOB错误率达到了12.02%，而随机选取96个SNP位点在进行分类时，降到了8.96%，说明保留的位点数越多其准确率也就越高。

方式2：从PCA预选出的520个SNP位点中随机抽取48个和96个SNP位点，再利用随机森林分类。可以看到OOB错误率有明显的降低，这也进一步说明，利用PCA评分选出的SNP位点与随机选取的SNP位点相比更具价值。

方式3：根据Gini指数减少的排名选取48和96个SNP位点。方式4：根据平均精度减少的排名选取48和96个SNP位点。OOB错误率相对于仅仅根据PCA评分选出的SNP位点来说，利用随机森林两种排名方式选出的SNP位点更具有价值能够进一步降低错误率，提高计算效率。

不同的分类方法与本文方法对比结果见表2。

可以看到相对于文献[20-21]，本文中每个品种的参考样本是较多的，这表明本文方法能够捕获到更多的品种差异信息，会降低由冗余SNP位点导致错分的可能性[22]。在文献[20]中不同品种的分类需要根据决策树的不同层次建立不同大小的SNP集合，这样才能够保证到达要求的准确性，这个过程较为复杂。本文的随机森林利用相似结构的决策树，解决了不同层次的分类问题，优化计算过程，节约计算成本。在文献[21]中根据设定的典型系数（Canonical Coefficients）阈值选取SNP位点。当有K个品种则需要K-1个阈值，随着品种数的增多阈值的个数也会相应增多。而本文都是由统一的排名方式选取SNP位点，而不需要特意设定阈值，对于数据的通用性更好。从表中可以看出在相同准确性的情况下，本文使用最少的SNP位点个数，以此提高计算速度，节约计算成本。

表2 不同方法的分类性能对比

4 结语

本文提出了利用PCA和随机森林相结合的方法，可以从庞大的数据集中筛选出含有高信息量的SNP位点用于品种分类。实验证实，对于将未知个体分配到与其对应的品种的正确率达到了97.35%～98.37%。与其他SNP筛选方法相比较，将PCA和随机森林很好地结合到一起，有效地减少用于分类的SNP位点数目，节约计算成本。并且本文方法即使随机森林使用较少的SNP位点，在分类上也有良好的表现。但是对于其他物种和数据是否也有很好的性能还需要进一步的研究。