基于AMESim软件的胶带机自移机尾动态仿真分析
闫 慧
(神东煤炭集团设备维修中心,陕西 神木 719315)
0 引言
胶带机自移机尾是整个综采工作面运输设备的一个重要环节,是胶带机的一个重要组成部分。在现代综采煤矿开采设备中,一般都是使用胶带机自移机尾与带式输送机连成一体,与中间架一起构成综采工作面的运输系统。
煤矿综采工作面在运输过程中,胶带机自移机尾起到了联接作用。通过胶带机自移机尾,实现通过破碎机、转载机运输来的煤传输到胶带输送机上面的一整套运行过程[1],这样就使得开采过程更加连贯和顺畅,所以对胶带机自移机尾进行动态仿真分析,是设计自移机尾非常重要的环节。
1 胶带机自移机尾模型建立
本文分析的是5.9 km带式输送机所配套的胶带机自移机尾,具体参数见表1。
建立相关的带式输送机动力学模型主要借助AMESim软件,具体情况如图1所示。
在其模型构建环节,首先须在其软件的每个模块中找出所对应的各个部件,之后进行网络连接。在连接实现后,应在其软件子模型的模块下对每个部分的函数模块进行有效选取,当其针对每一个组件的函数模型实行有效选择后才能进入参数指标设定过程。这是该软件不同于计算机SimuHnk软件[2]的地方,这样无需构建每个部件具体的函数模块,而是在其子模型模式条件下进行有效合理的自建。数学模型建立后,还需进行相关仿真参数的设置。
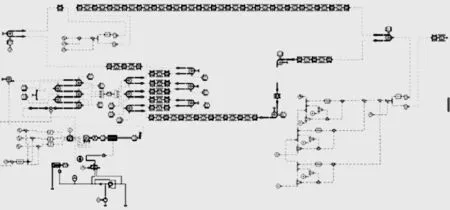
图1 自移机尾前移时胶带机仿真模型

具体参数具体值具体参数具体值输送带的实际单位质量/(kg·m-1)20.2输送带型号PVG2000S物料在输送带上的具体质量/(kg·m-1)233.1实际带宽度/mm1 600上托辑旋转部分等效质量/(kg·m-1)25.13输送带弹性模量/(kN·m-1)16 000带线路布置方f整机按水平布置自动张紧装置布置距机100 m处带速/(m·s-1)4下托辑旋转部分的等效质量/(kg·m-1)18.72储带的仓带长度/m200自移机尾的质量/t34.7首尾滚筒中心距/m5 900自移机尾行程/mm2 700
2 仿真参数设置
2.1 带式输送机部分
具体测算后,发现各单元粘性的阻尼指标系数是4 096 kN/m,刚度系数接近5 120 kN/m,然而在计算机承载部分的各输送带当中,等效质量约等于1 4521.3 kg,粘性的摩擦指标系数是943.75 N/(m/s),而库伦的摩擦力与静摩擦力约等于3 775 N;计算机回程部分输送带各单元等效的质量是1 996 kg,静摩擦力和库伦摩擦力近似于518.96 N,带式输送机的驱动滚筒的直径是1 000 mm,滚筒的转动的惯量接近于211/986;改向滚筒直径改为630/1 000 mm,游动车辆的部分质量约等于1 000 kg;机尾的滚筒直径约等于800 mm,转动的惯量是500 kg·m2,而自移机尾的单元质量是34.7 t,刚度的系数是5e+08 kN/m,粘性的阻尼指标系数是4e+08 kN/m,地面和自移机尾的摩擦指标系数是0.3,库伦摩擦力和静摩擦力近似等于1.04e+05N。
2.2 通过改变自动张紧装置频率来调整速度
制动器开启时承受的压力是3 MPa,减速比接近74,电机额定的转动的速度是1 485 r/min,液压系统承受的压力接近7.5 MPa,张紧绞车的滚筒的直径约等于530 mm,系统内的流量接近15 L/min,蓄能器蓄能提供的压力是9 MPa,整个泵站提供的压力为9.3~11 MPa。
2.3 胶带机自移机尾前移控制部分启动
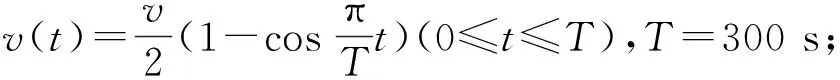
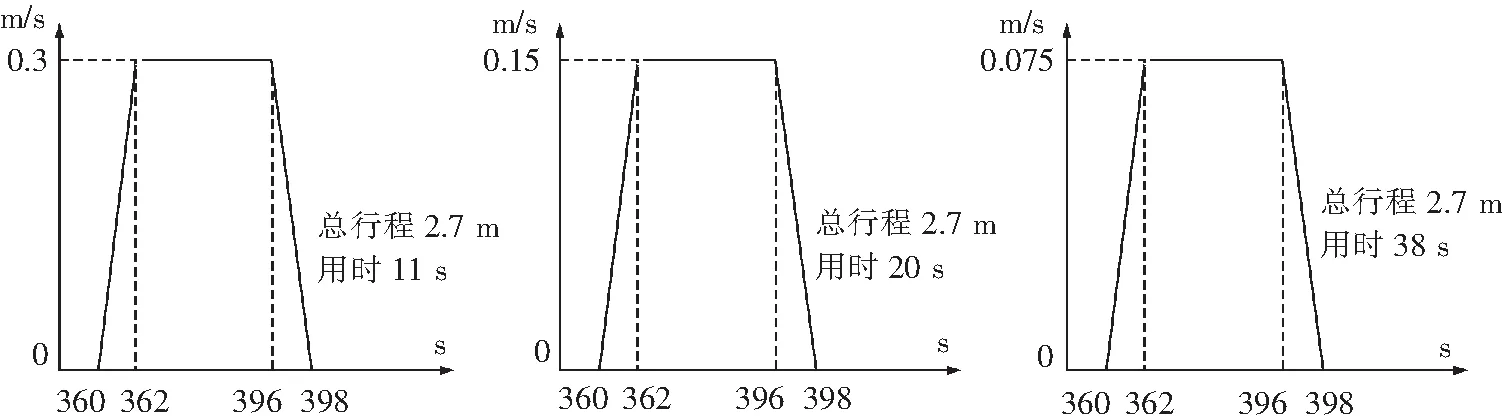
图2 自移机尾前移速度控制图
2.4 运行参数的设置
运用标准的积分仪器,而非一定步长的积分仪器,初始时间是0 s,结束期限是600 s,通信的间隔是0.6 s,期限的步长与通信的间隔是互相独立的。而其它参数都通过系统确认。时间跨步最大的是le+30 s,在标准的选项中,偏差值为le-05。
3 动态仿真分析
3.1 启动过程
启动之后,带式输送机处于稳定的状态之后,将移动小车和转载机的连接点作为支点,自移机尾会不断地往前移动,如图3所示。这个时候,输送带拉力和液压驱动力会不断地进行推动,让带式输送机在力的影响下逐步前进。依照先提速到平稳速率[4],再稳定运作一段期限后又慢慢减速到相对静止的规律运作,在自移的机尾运作环节中,带式输送机始终在运作,直至自移的机尾暂停运作,缓冲一些时间后达到平稳运作,这样进行仿真的过程。
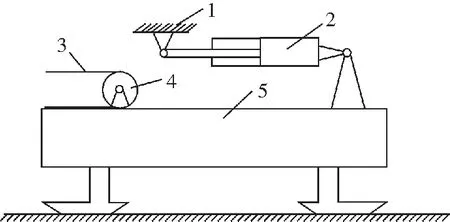
1-计算机转载机与滑移车辆等效的连接处;2-水平移动油缸;3-计算机的皮带;4-计算机机尾的滚轮;5-计算机的机架图3 自移机尾简化示意图
用正弦加速控制曲线开始启动,正式启动60 s之后,自移机尾开始向前移动,在使用的过程中带式输送机启动的时间接近300 s,3类状况总体前移的行程都是2.7 m,且平稳运作速度呈现出倍数的关系,比如0.3 m/s、0.15 m/s与0.075 m/s,依次对应着11 s、20 s与38 s,然后让其稳定运作到平稳的状态,运作速度的控制如图2所示。平稳速度和对应的期限呈现出对应的关系。
3.2 自移机尾运行20 s的仿真结果
图4为自移机尾运行时间为20 s时承载段头尾张力、速度的仿真结果,图5为机尾和张紧装置的张力仿真结果。
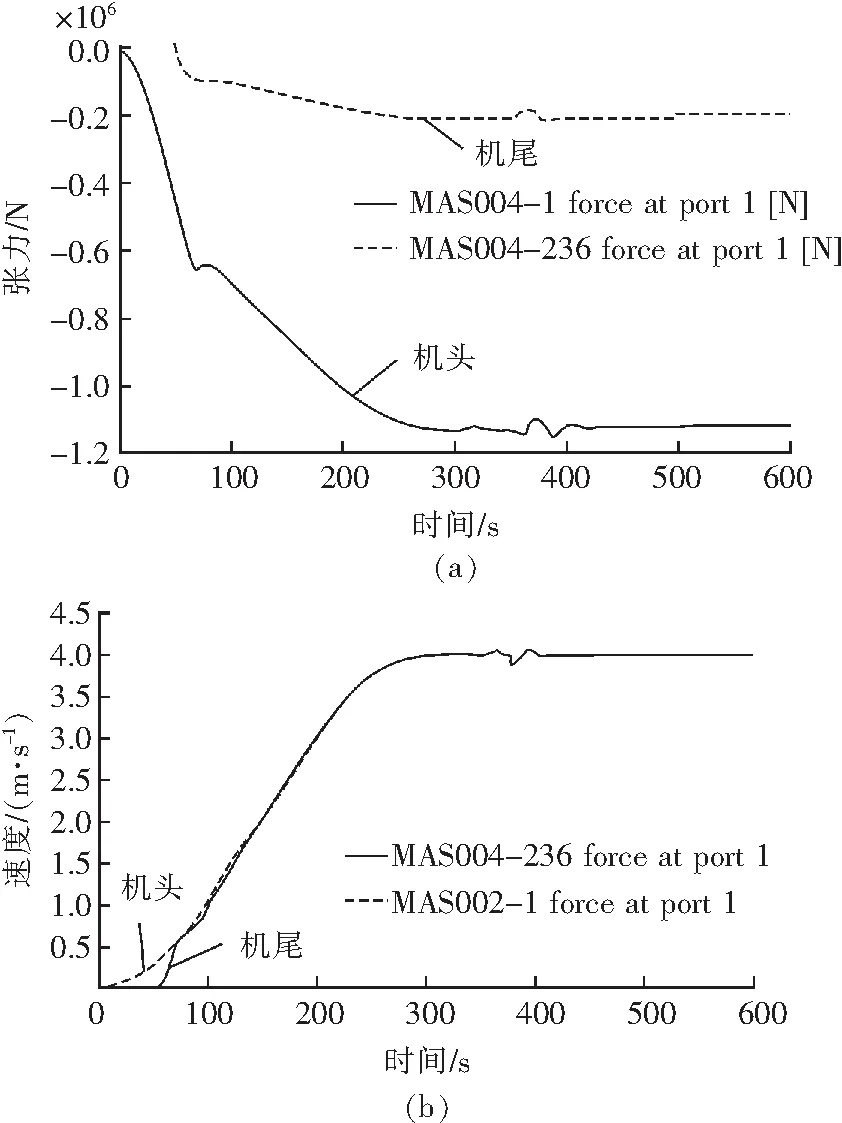
a-张力对比曲线;b-速度对比曲线图4 承载段输送带头尾张力、速度仿真曲线
从图4(a)可知,当自移的机尾发生前移的时候,机尾快速动作,通过3.33 s的应力波从机尾传输至机头,其满足张紧配置的设计要求。机尾输送带的张力要远远小于机头输送带的张力,当机头张力位于峰值时,张力是1.15×106N左右,逐步趋于平稳状态时的基本张力为1.125×106N,然而自移机尾在经过张力上下浮动以后,平稳后的张力是2.227×105N,而且能够知道胶带机启动的动态影响比机尾前移时影响要大得多。因而在注意启动的动态作用时,不可忽略自移的机尾移动影响。
从图4(b)看出,当自移机尾向前移动的时候,机尾输送带速率波动较大,而胶带机机头的输送带一般在该输送带稳定运作的4 m/s速度上下波动,能够看出机头没有产生打滑的问题,其仿真有效模拟了本质的状况。
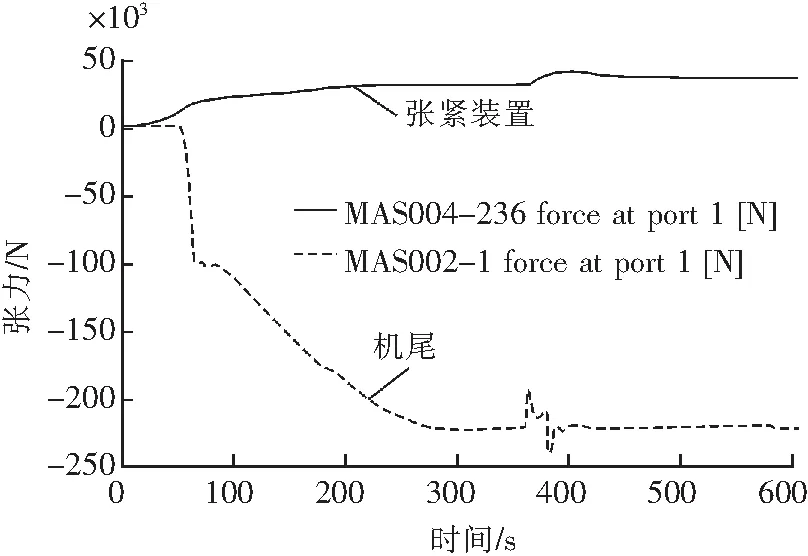
图5 机尾与张紧装置张力对比曲线
从图5可知,当自移机尾前移的时候,机尾会立刻产生张力的波动感应,通过2.8 s传输至机头装置处,符合了自动张紧设计的要求。
3.3 自移机尾不同速度前移的仿真结果
对仿真的模型进行运行,能够得到自移的机尾依次以0.3 m/s、0.15 m/s与0.075 m/s向前移动时机尾和机头部分输送带加速度、速度以及张力的比较曲线,如图6所示。每个图当中1、2、3依次表示自移机尾平稳运作时速度0.3 m/s、0.15 m/s与0.075 m/s,相对应的参数曲线。

a-机尾张力;b-机头张力;c-机尾速度;d-机头速度;e-机尾加速度;f-机头加速度图6 机尾不同速度前移时张力、速度、加速度仿真曲线
张力:①从图6(a)可知,当自移的机尾通过不一样的速度向前移动时,机尾尾部立刻做出一定的响应,反映出巨大冲击力,而输送带的张力快速降低,峰值体现的较窄,这样全面地体现了应力波瞬间性[5]。当自移机尾通过不一样的速率前移,平稳运作时,速度每提高一倍,该输送带的张力将提高一倍,且速率越大,其波动性就越剧烈,然后体现出往反向的基本紧带以及通过小幅波动到平稳运作,表明了尽量让自移机尾进行缓慢向前推移的道理;②从图6(b)可知,当自移机尾通过不一样的速率前移时,都通过3.33 s,应力波从机尾传输至机头,其满足张紧装置的设计制作要求。应力刚达到机头的时候,反映出瞬间的冲击力,机头输送带张力快速减少,平稳运作速度提高一倍,该机头拉力的峰值将提高一倍,之后体现出往反向运作的紧带,通过小幅振动以后处在平稳的运作状态,平稳的时候机头的输送带拉力是1 122 kN左右,3类控制要求下,最大的波动区域是4.63%,且在波动准许的区域内。与图6(a)进行比较后可知,在进行输送的时候,机尾受到的张力是远远小于机头张力的。自移机尾机头保持稳定状态之后,机头在输送的过程中,其中张力约等于1 122 kN,自移机尾的尾部张力是225 kN,因而要特别关注机头部分动态性能对于输送带张力的影响作用,输送带有可能由于张力过大而出现打滑现象,甚至造成严重的事故。
速度:①从图6(c)可知,当自移的机尾通过不一样的速度进行前移的时候,机尾的速率波动十分显著。当自移机尾按照不同的速度进行前移时,平稳运作的时候速度每提高一倍[6],该输送带的速率开始波动峰值将提升一倍,如果速度越大,其波动性将更加剧烈。显然,自移的机尾运作越缓慢,针对机尾滑动的问题就越小;②由图6(d)可知,以不同速度,自移机尾向前推移时,位于机头的传送带部分伴随有轻微的浮动,并且不难发现机头速度的峰值随着自移机尾前移的稳定速度的增加而增加,因此需要尽可能地令自移机尾缓缓向前移动。经历了小幅波动后,皮带最终回到4 m/s的速度,因此该模型可以用来真实地模拟实际运作情况。此外机头接收到应力波的时候,其速度已经有所减弱,通过0.3 m/s为最大冲击稳定速度的这组数据反映出来,机头带速的最大峰值是4.015 m/s,与之相对的机尾带速的最大峰值是4.16 m/s,就波动倍数这一项来看,机尾的波动倍数是机头的10.7倍。由此可知,自移机尾前移速度越小,对我们越有利,当然在实际情况中需要适当调整,速度不能太慢,结合不同情况设定不同的速度。
加速度:①由图6(e)可知,在自移机尾前移速度不同时,输送带加速度波动初始的峰值与稳定运行时刻速度成正比例,k值趋近于1,并且波动伴随着速度的增大也会更加强烈。自移机尾在稳定速度为0.3 m/s时存在着剧烈的瞬间冲击力,从这点就可以预料到这种情况对输送带可能产生的危害,因此,自移机尾在向前移动的时候一定要保证速度的缓慢。此外,自移机尾的前移速度增大的过程令输送带的加速度波动也增大,远大于带式输送机启动的波动,因此需要保证自移机尾前移速度在可控范围内;②由图6(f)可知,当以不同速度自移机尾向前推移时:机头输送带的运行加速度随着自移机尾前移稳定速度的增加而增加,输送带加速度波动的峰值与稳定运行时刻速度是成倍数增长的。由此可知,自移机尾运行速度的增大会给机头带来更大的冲击力,这是符合实际情况的,所以要求在设计的时候尽可能让自移机尾的前移速度慢下来。
机尾稳定前移带来的后果:①这3种成倍数速度条件的输送带的反应是同步的,机尾输送带做出的动作,均需要3.33 s应力波才会传到机头;②在稳定速度成倍增长的情况下,机头和机尾输送带的加速度的波动峰值、张力、速度的对应数值也相应的成倍变化,速度加大后会对输送带造成更大的危害;③机尾受到的张力只有可能是机头处受到张力的1/5。波动性会直接影响后期输送带的震动情况,机头处输送带的张力波动会因为运行速度达到一定值之后而超过输送机所开启时的张力波动,带来的后果将会很严重,因此控制住自移机尾前移速度十分必要,这样可以避免机头皮带打滑以及更为严重的问题产生。
3.4 驱动滚筒松边张力、速度、加速度仿真
自移机尾运行20 s时驱动滚筒松边张力、速度、加速度仿真曲线如图7所示。
由图7(a)可知,在自移机尾向前移动的时候,带中应力一到达机头部分就展现出了瞬间冲击力,位于机头的松边输送带张力剧烈减小,随后展现出朝着反方向的紧带,再经过很短时间的波动最终达到稳定状态。稳定运行的输送带松边张力不再是之前的78.2 kN而变为了79.5 kN,波动的最大峰值是3 kN,处于张力波动的许可范围中,所以机头的驱动滚筒没有发生打滑。与启动时相比,可以发现,自移机尾前移的张力波动不大,这可以看出张紧装置有进行紧带。
由图7(b)、7(c)可知,当自移机尾向前移动时,机头的加速度以及驱动滚筒松边的速度波动不大,可以推测机头的驱动滚筒没有发生打滑。
3.5 游动小车张力、速度、位移仿真
游动小车运行的张力、速度、位移仿真曲线如图8所示。
由图8(a)可知,在自移机尾开始前移后,应力波传达到张紧装置,张紧装置马上进行了紧带行为,游动小车随之向前挪动,张紧力从30 kN的初值快速增长到39 kN的峰值,此后因为紧带行为超过了张紧力范畴又出现松带,最后游动小车停止游动,回到平衡状态,所受张紧力为33 919.2 N。
由图8(b)可知,自移机尾向前移动时,应力波传输到张紧装置,游动小车开始实行紧带任务,可以看出在速度上所能产生的冲击是很大的,即使是很短的时间也会发生很大变化,速度会从初期的0不断增加,能达到的峰值是0.056 m/s,速度图像的斜率虽然不小,但是它对于张紧的影响力很小,当张紧行动达到上限的时候,张紧装置会执行反向松带的行为,最终经历很短时间的波动达到平衡状态,同时游动小车再次回到静止状态。由图8(b)反应出自移机尾前移所带来的影响比不上皮带机启动所带来的影响,所以要求在设计的过程中,带式输送机可能受到的影响也要了熟于心。对于机尾不断向前移动可能在动态上产生的变化也要了熟于心。
由图8(c)可知,自移机尾前移的时候,游动小车先是机头张紧,达到张紧上限后,反向松带,小幅度的波动后,游动小车停止移动,回到静止状态。这个过程中,游动小车紧带时,向前移动了0.893 85 m,大概是机尾前移位移的1/3,与实际情况相符。
3.6 机尾前移速度的控制
在自移机尾前移速度不同时,机头松边是同步的,带中应力到达机头就展现出了瞬间冲击力,位于机头的松边输送带剧烈减小,随后展现出朝着反方向的紧带,再后来经过很短时间的波动最终达到稳定状态。稳定运行的输送带松边张力不再是之前的78.2 kN而变为了79.5 kN,波动的最大峰值是3 kN,处于张力波动的许可范围中,所以机头的驱动滚筒未发生打滑。机头驱动滚筒松边的张力随自移机尾前移速度的增大而增大,为了避免事故的发生应保证自移机尾尽可能地慢速前移。
在自移机尾前移速度不同时,即便速度存在波动,但仍呈现出:速度波动峰值与自移机尾稳定运行速度同比增长的规律,速度的波动都很小,波动峰值最大达到0.000 03 m/s,打滑现象出现的比较多,其中较多可能出现的就是在机头驱动滚筒松边处。
在自移机尾前移速度不同时,机头松边的相应虽然是同步的,但是波动也是与自移机尾前移速度成比例的,自移机尾速度越大,加速度的波动也更为强烈,但波动的范畴都不大,即便是最大的波动峰值也才2.5×10-4m/s2,可以看出机头的驱动滚筒没有发生打滑。
4 结语
通过建立胶带机自移机尾模型,运用AMESim软件对胶带机自移机尾在使用过程中进行动态仿真分析,模拟自移机尾在使用过程中出现的工况,推测自移机尾前移时可能出现问题,这样可以很好地推测自移机尾前移时机头驱动滚筒是否会出现打滑,此外还可以证明变频调速自动张紧装置能够与机头驱动滚筒紧带与松带情况契合,将危险事故的发生扼杀在摇篮中,给胶带机自移机尾设计和应用奠定了基础。

