Alpha稳定分布下基于RHMy滤波的MQAM信号码元速率估计方法

廖锡畅 雷迎科 罗路为 黄健航

(国防科技大学电子对抗学院，安徽合肥 230037)

1 引言

多进制正交振幅调制(Mary Quadrature Amplitude Modulation, MQAM)信号相较于传统的多进制相移键控调制(Mary Phase Shift Keying, MPSK)而言，同时对信号的振幅和相位进行调制，极大的增加了系统的频带利用率，同时也具有较强的抗干扰能力与保密性，广泛应用于各种军事或民用的高速带宽通信系统中。在通信对抗领域，为达到通过盲解调技术获得对抗方情报的目的，首先需要准确估计信号的调制信息。但非协作端实际侦收时，信号受自然与人为因素(如低频大气噪声、雷暴、多用户干扰等)的影响[1]，常伴有很强的不规则冲激特性，使得噪声概率密度函数偏离高斯分布，且拖尾严重。Alpha稳定分布作为唯一满足广义中心极限定理的分布[2]，通过调节其特征指数可以得到不同厚度的拖尾与不同程度的脉冲特性，与自然界中很多实际噪声环境吻合，因此针对Alpha稳定分布环境下的信号码元速率估计研究更具现实意义。作为数字信号调制信息的重要参数，码元速率的准确估计对信号的调制识别与解调意义重大。目前已有多种有效的码元速率估计算法，主要包括循环谱估计法、包络法、小波变换法等。文献[3]提出的Haar小波变换法(Haar Wavelet Transform, HWT)，通过观察信号瞬时相位变化规律估计码元速率，算法复杂度低，精度较高，但抑制脉冲噪声能力差。类似的，基于高斯噪声模型的算法在脉冲噪声环境下效果普遍较差，甚至完全失效。近年来，国内外学者作出了不少研究，主要包括Myriad滤波[4]、分数低阶统计量[5]、广义高阶循环累积量[6]、稳健L-DFT滤波[7]等方法。文献[8]提出一种基于分数低阶循环谱(Fractional Lower-Order Cyclic Spectrum, FLOCS)的MPSK信号参数估计算法，同时估计载频和码元速率，但算法计算复杂，分数阶数的选取对估计精度影响较大。文献[9]提出了广义平方包络谱的概念，分析广义平方包络谱与符号率脉冲线的关系，间接估计信号的符号率。但是该算法在α较小时性能急剧下降，且对于QAM信号的效果要明显差于PSK信号。文献[10]提出一种基于柯西分布的码速率最大似然估计法，可同时估计码速率和定时偏差，需要准确的划分时偏窗与同步窗，且在广义信噪比较低的条件下精度不佳。

针对Alpha稳定分布噪声下传统的MQAM信号码元速率估计算法失效的问题，本文首先结合加权Myriad滤波能有效抑制脉冲噪声的特性，引入二次小波变换对Alpha稳定分布条件下的MQAM信号进行码元速率估计(Weighted Myriad filter-Wavelet Transform, WMy-WT)；然后提出一种基于递归混合Myriad滤波器的二次高阶消失矩小波变换法(Recursive Hybrid Myriad filter-Wavelet Transform, RHWy-WT)估计码元速率。与HWT、FLOCS等算法进行比较，仿真实验表明，本文算法能够有效抑制脉冲噪声对信号的影响，并准确的估计出MQAM信号码元速率。

2 MQAM系统模型

假设非协作通信段截获的MQAM观测信号为：

(1)

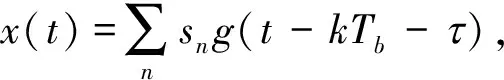
由于Alpha稳定分布没有闭合的概率密度函数，目前有四种定义方式，最常用的是采用特征函数来描述[2]：

φ(t)=exp{jat-γ|t|α[1+jβsgn(t)ω(t,α)]}

(2)

其中α∈(0,2]为特征指数，用来度量Alpha稳定分布的冲击程度与拖尾厚度，其值越小，冲击程度越强，拖尾越厚；β∈(-1,1]为对称参数，描述扭曲程度，一般而言采用β=0的对称Alpha稳定分布(Symmetricα-Stable,SαS)；分散系数γ∈(0，+)为分散系数，类似于高斯分布的方差，用于分布描述偏离均值的程度；a∈(-,+)为位置参数，对于SαS分布，α∈(0,1)时，a为中值，α∈(1,2]时，a为均值。

当α=2时，SαS即为高斯分布；当α=1，β=0时即为柯西分布；当α=1/ 2，β=-1时即为皮尔逊分布。图1表示不同α值时的SαS时域波形图。显而易见，α越小，脉冲突刺现象越明显，幅度也越大。图2为对应的概率密度函数曲线，随着α的减小，曲线拖尾明显变厚且峰值变得越来越尖锐[10]。

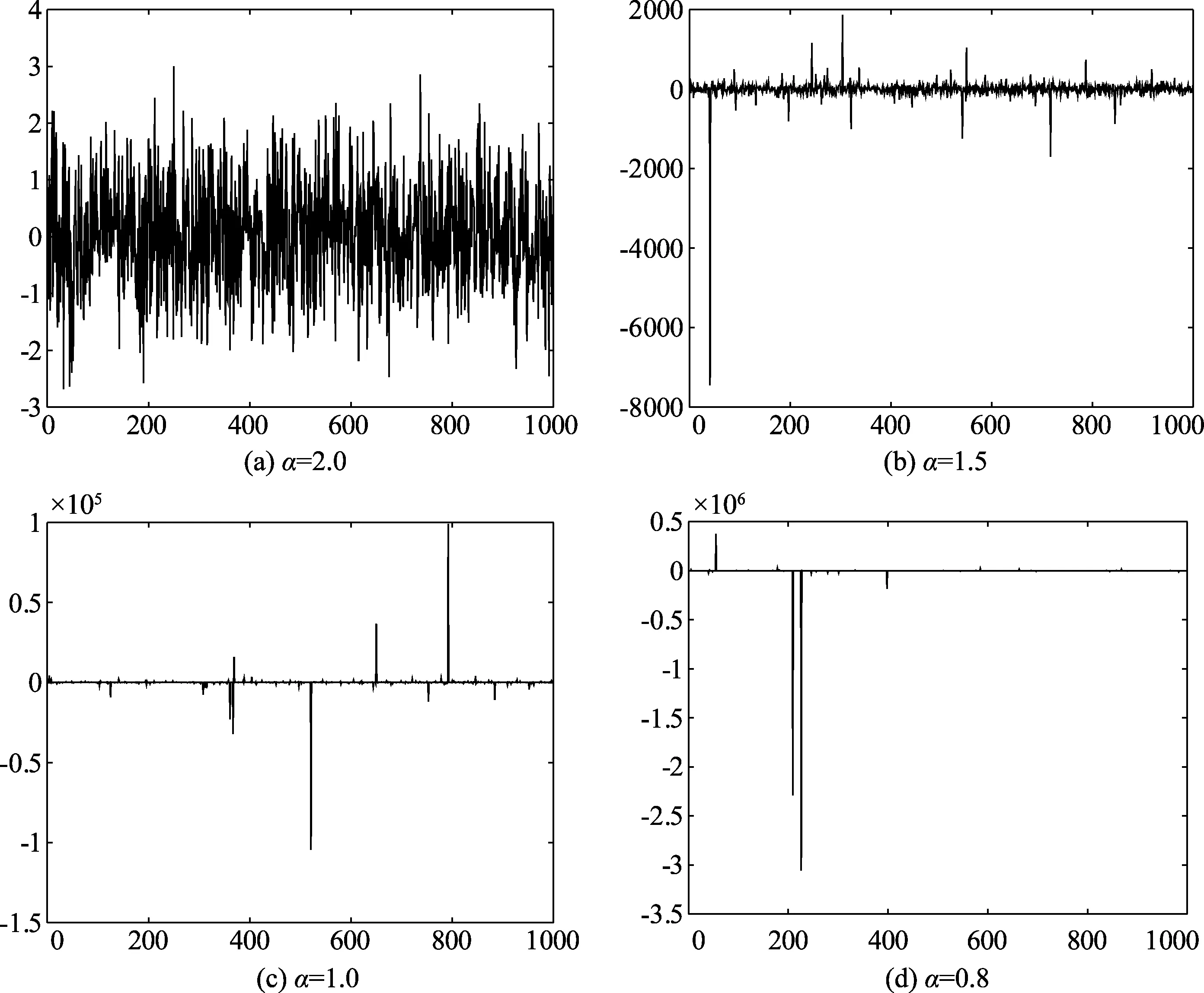
图1 不同α值时的时域波形Fig.1 Time domain waveform at different α values

图2 不同α值的SαS概率密度曲线Fig.2 Probability density curve of SαS at different α values

3 M-filter类算法原理

类似于FIR滤波器在高斯噪声模型中的应用，M-filter类(如Myriad、Meridian等)算法以其良好的频率选择性与脉冲噪声抑制性能，同样广泛应用于脉冲噪声环境下的信号和图像处理领域。本节通过研究M-filter类算法，创新性的将递归混合Myriad滤波算法引入脉冲噪声的码元速率估计。

3.1 加权Myriad滤波器

柯西分布作为Alpha稳定分布中具有封闭概率密度函数的典型代表之一，现有的M-filter类算法均基于广义柯西分布提出，通过建立可调的次优对数似然函数进行最大似然估计，并推广到一般情况。学者们验证表明，M-filter类算法具有较好的鲁棒性，能够很好的适应不同程度的Alpha稳定分布噪声[11]。柯西分布的概率密度函数为：

(3)

式中k对应于Alpha稳定分布的分散系数γ，根据式(3)构建Myriad代价函数来估计稳定分布最大值位置，舍弃常数项后，其对数似然函数为：

ρ(x)=lg{k2+|x|2}

(4)

(5)

其中◇为定义的加权算子，线性可调参数K∈(0,+)决定了WMy滤波算法的性能好坏，即代价函数ρ(K,β,w)的最小值就是算法输出值。K→时，MWy滤波算法表现为线性特性，退化成标准线性FIR滤波；K→0时，MWy滤波算法表现为众数特性，其输出为其中M为重复次数最多的符号化样本集合。结合自适应迭代算法可对WMy滤波算法进行优化，实时迭代更新最优权值，其迭代关系为：

(6)

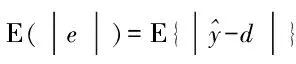
wi(n+1)=wi(n)+sgn[sgn(wi)xi-y]

(7)

3.2 递归混合Myriad滤波

由于加权Myriad滤波算法在强脉冲噪声条件下性能下降，脉冲噪声经过一层Myriad滤波后，趋向于满足正态分布。基于这一特性，文献[13]提出了一种全新的递归混合Myriad滤波算法(RHMy)，结合线性滤波与非线性滤波的优点，同时实现了WMy滤波对脉冲噪声的抑制能力与线性滤波在高斯环境下的优良特性。

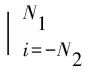
(8)

可通过调节参数K来控制滤波器抑制脉冲噪声的性能，RHMy滤波的输出为似然函数Ψ(x,y,β)的最大值，其中β为输入样本的位置参数。为方便处理，对似然函数取对数并去掉常数项，将局部最大值问题变为求取局部最小值，则估计输出可表示为：

(9)

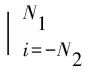
(10)

(11)

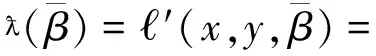
(12)

(13)

(14)

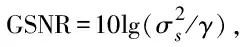
如图3所示，Alpha稳定分布噪声环境下正弦波波形严重失真，WMy滤波后有效的恢复出了原始波形，但效果较差，波形畸变仍较为严重。本文采用的RHMy滤波算法性能明显提高，能够更好的抑制脉冲噪声对信号的影响，可以直观的看出此时较好的恢复出了正弦波信号，为脉冲噪声环境下的信号通过小波变换检测瞬时相位，并精确的估计码元速率提供了必要前提。

图3 滤波器效果对比图Fig.3 Contrast diagram of filter effect

4 码元速率估计

小波变换作为一种重要的时频分析手段，具有良好的瞬时相位检测能力，根据信号的周期变换规律，经过简单的系数处理即可较为准确的估计码元速率，且运算量小，实现复杂度低，广泛的应用于实际工程中。本节通过分析Haar小波基消失矩较小等问题，结合小波变换后的信号特征，采用具有高阶消失矩的dbN小波基，结合二次小波变换来分析信号边界暂态特性，并给出了本文提出的基于RHMy滤波的码元速率估计算法实现步骤。

根据式(1)中给出的系统模型，信号x(t)的连续小波变换[3]可表示为：

(15)

其中ψ(t)为小波基函数，s为小波尺度参数，τ为小波转换参数。经典的算法中主要采用最为简单的Haar小波作为基小波，MQAM信号的Haar连续小波变换为

(16)

小波变换的实质是通过提取数字信号边界上的暂态特性，即根据幅度、频率或相位的瞬时变化提取码元速率特性[15]，根据上述分析，MQAM信号经过一次小波变换后，其幅度值表现为仅在码元交界处表现为冲激特性，而在码元周期内表现为恒定幅度值，因此可近似表示为：

(17)

其中Am表示第m个符号小波变换后的幅值，Bn表示码元交界处的幅值，u(·)和δ(·)分别表示阶跃函数和冲激函数。根据式(17)，信号经过一次小波变换后，其边界仍然具有暂态特性，此时可以通过二次小波变换来提取信号码元速率信息，根据文献[15]中的分析，二次小波变换后的信号仅表现为冲激特性，其包络可近似的表示为：

(18)

其中Ci为第i个符号经过二次小波变换后的幅值。根据式(18)，在无噪条件下对MQAM信号进行二次小波变换后，此时的信号小波系数呈现冲激特性，仅在信号码元速率的整数倍处取值，因此对其模值进行傅里叶变换后，可根据冲激谱线间隔精确的估计出信号的码元速率。

根据上述分析，Alpha稳定分布下基于RHMy滤波的MQAM信号码元速率盲估计算法实现步骤为：

(1)对截获信号进行递归混合Myriad滤波，抑制Alpha稳定分布引入的脉冲噪声；

(2)选择具有高阶消失矩的dbN小波系(本文采用db5小波)，对采样后的信号进行一阶离散小波变换，并对小波系数取模；

(3)对模值进行第二次db5一阶离散小波变换，并对二次变换后的小波系数取幅度平方；

(4)对幅值平方进行傅里叶变换(FFT)，分析频谱并搜索最大值点N1和次大值点N2；

5 仿真分析

本文仿真中采用64QAM调制信号，码元速率fb=2e6 Hz，载波频率fc=1e7 Hz，采样频率fs=4e7 Hz，升余弦脉冲成型滤波器滚降系数为0.5，仿真采用SαS分布噪声分布模型。

首先将本文方法(RHWy-WT)与传统多尺度Haar小波变换法(HWT)、基于分数低阶循环谱的码元速率估计法(FLOCS)和基于自适应加权Myriad滤波算法的小波变换方法(WMy-WT)进行比较。其中FLOCS首先定义了b=0.1阶分数低阶算子，对观测信号进行分数低阶循环自相关运算后进一步求得分数低阶循环谱，然后通过搜索谱切面估计码元速率。WMy-WT算法首先对观测信号进行自适应加权Myriad滤波，需要注意的是，不同的初始权向量会影响算法的收敛速度，所以在未知条件下，初始权向量一般设置为中间位置权值非零，其余均为零[12]，经过迭代后，所有权值逐渐收敛至固定值，且窗口长度过长时会导致计算量大幅增加，过短又会影响滤波的效果。为达到快速收敛的目的，本文仿真设置滤波窗口长度为7。根据文献[12]，WMy滤波初始权向量设为w=[0,0,0,10,0,0,0]，迭代过程中，中间权值w4向下减小，其余值向上增大，最终各自收敛到最优权值，然后采用本文提出的二次高阶消失矩小波变换进行估计。RHWy-WT算法的Myriad部分窗口设置WMy滤波算法一致，即g=w；根据以上分析，线性滤波部分权向量窗口长度设置为4，初始值设为h=[0,0.5,0.5,0]。在特征指数α=1，广义信噪比GSNR=-1 dB的SαS分布噪声环境下对各算法进行仿真。

图4 各算法谱线图Fig.4 Spectral line graph of each algorithm

图4(a)表示在不使用WMy滤波前提下的多尺度Haar小波估计法的谱线图。可以看出，由于脉冲噪声的影响，原本适用于高斯环境的算法此时已经完全失效，正确的无法估计码元速率。图4(b)采用b=0.1阶分数低阶循环谱估计，类似于高斯环境下的循环谱估计算法，在频率切面上搜索循环频率对应的次大值。相比于图4(a)在实际码元速率Fb=2e6 Hz附近可以清楚的看到谱线，但是由于对脉冲噪声的抑制效果有限，实际码元速率对应的谱线并不是循环谱切面上的次大值，因此该算法在广义信噪比较低的情况下性能不佳。图4(c)表示基于自适应加权Myriad滤波算法的高阶消失矩小波估计(WMy-WT)法，与图4(a)相比，WMy滤波算法能够抑制脉冲噪声对信号的影响，但最大值谱线附近存在较大的谱线，说明在GSNR=-1 dB时无法有效抑制脉冲噪声。图4(d)采用基于递归混合Myriad滤波算法的高阶消失矩小波估计(RHMy-WT)法。此时的谱线图中在实际码元速率附近的峰值明显，且由于噪声带来的小波谱线干扰不足以淹没码元速率对应的谱线，证明RHMy滤波算法抑制脉冲噪声的效果相较于WMy滤波算法显著提高，能更加精确的估计码元速率信息。

RHWy-WT算法主要包括RHMy滤波与离散小波变换两部分，相比于WMy，RHMy在每个信号点上的计算量增加了M*(NJ+NM)，其中NJ与NM为RHMy中线性滤波部分一次运算与权值hj迭代一次的计算量，而离散小波变换相当于分离信号高低频系数，其时间复杂度可表示为O(L)，L表示信号观测长度。

下面通过归一化均方根误差来考察SαS分布噪声下广义信噪比对不同参数估计算法的影响。在不同的广义信噪比下，对64QAM信号进行100次蒙特卡洛实验。如图5可知，当脉冲噪声特征参数α<2时，HWT法完全失效，无法正确检测信号的相位突变点，而当α=2时，此时为高斯噪声，HWT法能够较为精确的估计出码元速率。如图5(b)、(c)、(d)所示，b=0.1阶FLOCS法在α>1时表现良好，在GSNR≥0 dB时能够精确的检测谱线，但从图5(a)中可以看出，随着α的减小，由于低阶循环谱中峰值谱线被噪声淹没，估计精度下降，且总体来说，FLOCS法的精度低于WMy-WT与RHWy-WT方法。

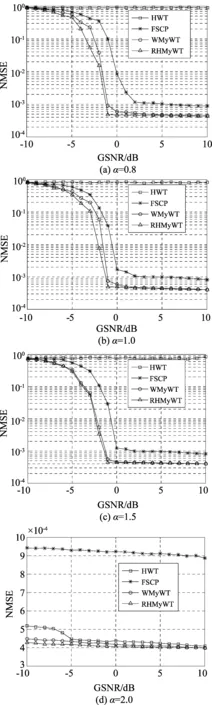
图5 不同α值环境下的算法比较Fig.5 Comparison of algorithms under different αvalue environments

WMy-WT方法结合了Myriad滤波算法和高阶消失矩小波变换的优点，在GSNR≥-1 dB时均可以达到精确的估计，但是对比与RHWy-WT方法，在α<1时，估计误差明显增大，这也证明了RHWy滤波算法虽然引入了一些计算量，但性能更优于WMy滤波算法，当α增大时，噪声接近高斯白噪声，两种方法性能接近，均能有效的估计出信号码元速率。

6 结论

本文主要研究了在Alpha稳定分布环境下的高阶QAM信号码元估计问题，针对传统的参数估计算法在脉冲噪声环境下失效的问题，提出了一种基于RHMy滤波的高阶消失矩二次小波变换法来估计信号码元速率。方法结合了Myriad滤波算法对脉冲噪声的抑制作用，将递归混合Myriad滤波算法引入，首先对信号进行滤波处理，采用运算简便，精度高的高阶消失矩二次小波变换法对信号进行码元速率估计。仿真实验表明该方法在较低的广义信噪比条件下仍能有效的抑制Alpha稳定分布噪声，较为精确的估计出MQAM信号的码元速率。

[1] 孔豫京, 黄焱, 马金全. Alpha稳定分布噪声背景下衰落信号的调制识别方法[J]. 信号处理, 2015,31(8):975-985.

Kong Yujing, Huang Yan, Ma Jinquan. Modulation Recognition Method of Fading Signals under Alpha Stable Distribution Noise Background[J]. Journal of Signal Processing, 2015,31(8):975-985.(in Chinese)

[2] 杨伟超. Alpha稳定分布噪声下通信信号调制识别研究[D].哈尔滨：哈尔滨工程大学,2012.

Yang Weichao. Modulation Recognition for Communication Signals in the Alpha-stable Distribution Noise[D]. Harbin：Harbin Engineering University, 2012. (in Chinese)

[3] Xu J Y, Zhang Y, Jiang H J. Symbol Rate Estimation Based on Wavelet Transform[C]∥International Conference on Wireless Communications, Networking and Mobile Computing. IEEE, 2012:1- 4.

[4] Zorlu H. Optimization of weighted myriad filters with differential evolution algorithm[J]. AEU-International Journal of Electronics and Communications, 2017, 77:1-9.

[5] 刘高辉, 张娟娟.α稳定分布噪声下数字频移键控信号的分数低阶循环谱分析[J]. 电波科学学报, 2017, 32(1):65-72.

Liu Gaohui, Zhang Juanjuan. Fractional lower order cyclic spectrum analysis of digital frequency shift keying signals under the Alpha stable distribution noise[J]. Chinese Journal of Radio Science, 2017, 32(1):65-72.(in Chinese)

[6] 李兵兵, 马洪帅, 刘明骞. Alpha稳定分布噪声下时频重叠信号的载波频率估计方法[J]. 电子与信息学报, 2014, 36(4):868- 874.

Li Bingbing, Ma Hongshuai, Liu Mingqian. Carrier frequency estimation method of time-frequency overlapped signals with Alpha-stable noise[J]. Journal of Electronics and Information Technology, 2014, 36(4): 868- 874.(in Chinese)

[7] 金艳, 朱敏, 姬红兵. Alpha 稳定分布噪声下基于L-DFT的LFM-BPSK复合调制信号参数估计[J]. 振动与冲击, 2015, 34(17):38- 43.

Jin Yan, Zhu Min, Ji Hongbing. Parametric estimation of LFM-BPSK hybrid modulated signals based on L-DFT under Alpha stable noise[J]. Journal of Vibration and Shock, 2015, 34(17):38- 43.(in Chinese)

[8] 赵春晖, 杨伟超, 成宝芝. Alpha稳定分布噪声背景下MPSK信号参数估计[J]. 沈阳工业大学学报, 2013, 35(2):194-199.

Zhao Chunhui, Yang Weichao, Cheng Baozhi. Parameter estimation of MPSK signals in Alpha stable distribution noise environment[J]. Journal of Shenyang University of Technology, 2013, 35(2):194-199.(in Chinese)

[9] Yang W, Yang X. Research on symbol rate estimation based on the generalized square envelope spectrum[C]∥IEEE International Conference on Communication Problem-Solving. IEEE, 2015:391-394.

[10] 金艳, 朱敏, 姬红兵. Alpha稳定分布噪声下基于柯西分布的相位键控信号码速率最大似然估计[J]. 电子与信息学报, 2015, 37(6):1323-1329.

Jin Yan, Zhu Min, Ji Hongbing. Cauchy Distribution Based Maximum-likelihood Estimator for Symbol Rate of Phase Shift Keying Signals in Alpha Stable Noise Environment[J]. Journal of Electronics and Information Technology, 2015, 37(6):1323-1329.(in Chinese)

[11] Pander T, Przybyla T. Impulsive noise cancelation with simplified Cauchy-based p-norm filter[M]. Elsevier North-Holland, Inc. 2012, 92(9):2187-2198.

[12] Kalluri S, Arce G R. Adaptive weighted myriad filter algorithms for robust signal processing in α-stable noise environments[J]. Signal Processing IEEE Transactions on, 1998, 46(2): 322-334.

[13] Ramirez J M, Paredes J L. Recursive Weighted Myriad Based Filters and Their Optimizations[J]. IEEE Transactions on Signal Processing, 2016, 64(15):4027- 4039.

[14] 许小东, 路友荣, 戴旭初,等. 一种基于最优尺度小波变换的符号率估计算法[J]. 中国科学技术大学学报, 2008, 38(10):1147-1152.

Xu Xiaodong, Lu Yourong, Dai Xuchu, et al. A symbol rate estimation algorithm based on wavelet transform with optimal scale[J]. Journal of University of Science and Technology on China, 2008, 38(10):1147-1152.(in Chinese)

[15] 纪勇, 徐佩霞. 基于小波变换的数字信号符号率估计[J].电路与系统学报, 2003, 8(1):12-15.

Ji Yong, Xu Peixia. Symbol Rate Estimation of Digital Signal Based on Wavelet Transform[J]. Journal of Circuits and Systems,2003, 8(1):12-15.(in Chinese)