3D MIMO多小区多用户系统基于QBFO算法的垂直波束下倾角优化
帅 杨 李 汀 李 飞
(南京邮电大学通信与信息工程学院, 江苏南京 210003)
1 引言
随着互联网的蓬勃发展和用户需求的进一步提高,人们对通信质量有了更高的要求。在此环境下通信技术近年来取得了诸多突破,多输入多输出(Multiple Input Multiple Output,MIMO)技术则是近年来现代通信中重大技术突破之一。
MIMO 在收发两端可以提供阵列增益,空间复用增益,分集增益和降低干扰的能力[1]。因此,MIMO技术现已成为无线通信中的关键性技术,但是在文献[2]中指出在一个存在邻小区同频干扰的通信环境中,MIMO系统的频谱效率会急剧降低,在某些情况下甚至降低到和单天线相同的水平。这表明,MIMO技术在现实通信系统中可能会成为一个干扰受限系统。针对这一问题,现如今已有许多传输方案,这些方案都利用了多天线这一特点,比如空间复用和波束赋形[3- 4]。特别是波束赋形可以利用信道信息降低小区间干扰从而提高系统性能。
但是在传统的2D MIMO中,只考虑了水平维度的波束,而忽略了垂直维度的波束。因为在现实世界中,无线信道具有三维的性质,而3D MIMO系统可以动态调节下倾角,充分利用了空间三维自由度[5],并且传统的波束赋形不能充分利用空间自由度。因此,有人提出了3D波束赋形[6]。在3D波束赋形技术中,可以将波束分为水平维度的波束和垂直维度的波束,能够有效的降低小区间的干扰,提高小区用户的频谱效率和系统的总吞吐量。实现3D波束赋形的一种方法是使用垂直波束赋形来提高期望信号的功率,同时减少小区间的干扰泄漏功率。那么关键问题就是如何自适应的调整天线下倾角。其中文献[7]指出,如果选择恰当的天线下倾角,就可以同时改善小区平均吞吐量和小区边缘用户吞吐量。文献[8-9]在单小区多输入单输出系统场景下,通过设计3D波束赋形优化天线下倾角,来提高系统吞吐量,但是没有考虑多小区的情况,有一定的局限性。针对多小区情况,文献[11]分析发现大尺度衰落因子可以只和天线下倾角有关,并在发射端采用了ZF预编码进行仿真分析,但未考虑用户间干扰的情况。本文的工作主要有两点:第一点是在多小区场景下,采用MRT预编码,推出了和速率公式,在考虑用户间干扰的情况下分析了系统性能并且与文献[11]进行了比较;第二点本文提出了采用量子菌群觅食优化(Quantum Bacterial Foraging Optimization, QBFO)算法来优化天线下倾角,通过仿真分析,量子菌群优化算法的寻优性能要优于文献[11]的二分搜索法。
2 系统模型
本文考虑一个多小区多用户系统。假设系统中有B个小区,每个小区有K个随机分布的独立用户,本系统中,基站端天线数量为Nt,高度为z(b),每个用户有一根接收天线,离地面高度为zk。如图1所示。天线阵列采用均匀线性阵列(Uniform Liner Array,ULA),垂直地面放置,其信道脉冲响应为:
其中d是阵元间隔间距,λ表示波长,θ表示平均发射俯仰角,Δθ表示发射俯仰角扰动值,服从N(0,ξ)正太分布,ξ是发射俯仰角扰动方差。3D ULA阵列如图2所示。

图1 系统模型Fig.1 System model
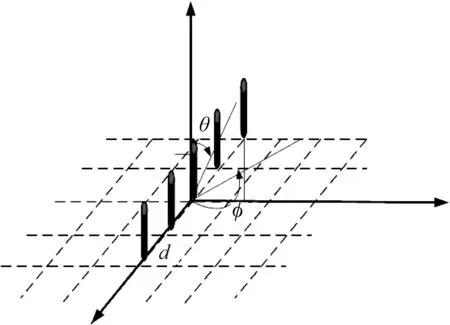
图2 3D MIMO ULA阵列模型Fig.2 The 3D spatial model of ULA
2.1 接收信号模型
(1)

2.2 3D天线衰落模型

(2)

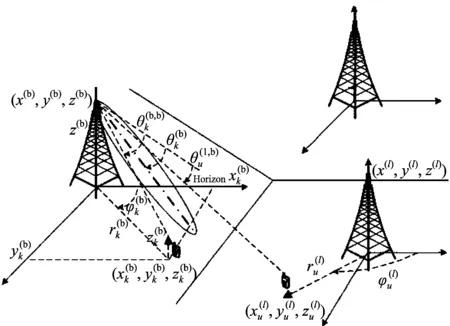
图3 3D传输模型Fig.3 3D progation model
(3)

(4)
(3)3D天线增益:为了便于分析,用户端使用的天线是各向同性的,而基站使用的是3D定向的天线阵列。第三代合作伙伴计划(3GPP)提出了3D定向天线图,并且用于3D波束赋形。根据文献[11],小区b第k个用户与基站l之间的3D天线增益包括两个部分:水平增益和垂直增益。分别用(5)、(6)表示:
(5)
(6)

(7)
那么3D天线增益就可以表示为:
(8)
从(5)、(6)、(8),不难发现天线增益需要最大化和最小化处理,这就增加了分析的复杂性。此外,水平维度的波束增益在以往的研究中已经很成熟了,所以本文主要针对垂直维度的波束增益。因此,我们在本文不考虑水平维度的天线增益,SLLV为无穷大。那么3D天线增益可以用如下式(9)表达:
(9)
影响慢衰落的主要因素包括:天线高度,基站的覆盖半径,用户位置,天线下倾角等。本文主要是针对天线下倾角的优化问题,因此本文假定其他参数都给定了,那么式(2)可以改写为:
(10)
这样,慢衰落信道增益公式的自变量就是天线下倾角。
3 和速率近似解公式
由公式(10)可知,当其他参数给定的时候,系统慢衰落系数只与天线下倾角有关。下面本文将会分析系统和速率和天线下倾角之间的关系。本文采用ULA天线阵列,发射端采用MRT预编码。本文中,假设每个下行链路数据流的功率相等。因此,小区l的预编码矩阵可以表示为:
(11)
其中:
(12)

(13)
其中:
Ekb=gkb,bpkb,b(hkb,bυkb)(hkb,bυkb)H=
(14)
(15)
(16)
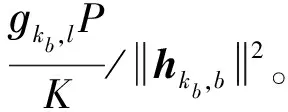
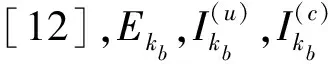
(17)
用户间干扰功率的伽马分布的形状和尺度参数为:
(18)
小区间干扰功率的伽马分布的形状和尺度参数为:
(19)
我们得到需求功率和干扰项的功率期望分别为:
(20)
则式(13)可以进一步写为:
Rkb(Θ)≈
(21)
那么总的系统和速率可以表示为:
(22)
然后我们提出了用QBFO算法[14]来求解最优解。
4 天线下倾角优化方案
早在2002年,就有人提出了细菌觅食优化算法[15]。该算法通过模拟大肠杆菌觅食行为来解决现实中的一些优化问题。2016年,文献[14]提出了量子菌群觅食优化算法(QBFO),文中将量子计算与菌群优化算法(BFO)进行结合。近几年,更多的研究表明QBFO算法有更好的寻优性能。
本节将采用QBFO算法求解式(22)最大化问题。
4.1 QBFO概念
QBFO算法是将量子理论和BFO算法相结合的智能优化算法。通常QBFO算法包含四步:
1)量子态表示大肠杆菌:大肠杆菌个体通过量子态来表示问题的解。
2)量子趋化:使用量子旋转门更新大肠杆菌群体状态Q(t)。对Q(t)进行测量,得到种群群体P(t),根据P(t)求得适应度函数值;再根据适应度函数值评估大肠杆菌群体,更新适应度值。然后通过量子门选择进行趋化操作。不断更新个体位置。
3)量子繁殖:将趋化操作所得到的使用度函数相加得到健康值函数。再将健康值函数排序,保留优秀的前一半,并且无性分裂为两倍,后一半淘汰。
4)量子驱散:设置一个驱散概率Ped,以Ped为判定标准,每个大肠杆菌个体生成随机数,如果该数小于Ped,则执行驱散。驱散的个体要再次随机生成新的大肠杆菌,这样可以保持群体数目不变。
4.2 使用QBFO寻找最优天线下倾角
根据式(21),可知目标函数和约束条件为:
(23)
将量子菌群寻优算法应用到本文的优化方案,我们把天线下倾角视为量子菌群染色体,系统和速率视为适应度函数,通过趋化、复制、驱散策略不断搜索最优染色体得到最优的天线下倾角,从而求得最大的系统吞吐量。
本文考虑一个多小区多用户系统。假设系统中有3小区,那么需要对3个小区的天线下倾角这三个参数进行优化,因此维度为3。染色体长度len,初始化种群个数为n,趋化次数为Nc,繁殖次数Nre,驱散次数Ned,大肠杆菌种群个数n,迁徙概率Ped,以及种群Q(t)。
算法流程的具体步骤如下:
Step1参数初始化:Nc=50,Nre=5,Ned=2,Ped=0.2。
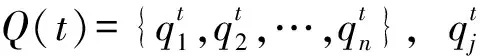
Step3测量Q(t),坍塌生成经典态P(t),P(t)为0和1组成的随机二进制的序列;
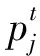
Step5量子旋转门进行趋化操作,实现对大肠杆菌种群Q(t)的更新,评估P(t),记录该代的适应度最优值,若优于上代,则保存该代,否则仍保留上代最优值;
Step6当趋化次数达到Nc时,趋化操作完成否则执行Step5,求解最佳适应度值,把最佳适应度值较差的一半染色体淘汰掉,对较好的一半染色体进行复制。
Step7繁殖次数小于Nre,继续执行Step6,否则执行Step8。
Step8对种群中每个染色体进行一次驱散判断,生成0~1之间的判定值,若判定值小于驱散概率Ped,则执行细菌驱散,重新生成一个个体。
Step9驱散次数小于Ned,转到Step6再次进行趋化和复制,否则执行Step10。
Step10此时目标函数的最大值即为小区最大和速率,此染色体对应的十进制数向量的值分别是三个小区的最优天线下倾角。
5 仿真分析
本文对大尺度衰落下3D MIMO多小区多用户系统中的3D 波束赋形技术进行了仿真分析。考虑3个边长为250 m的六边形小区,每个小区的功率采用的是均匀分配。那么每个用户的传输功率表示为P=Pt/(KM)。Pt是基站发射的总功率设为43 dBm。M是系统带宽的子载波数量设为1200。在路径损耗和衰落模型中,设L0=1.42×10-4,α=3.76。热噪声谱密度为-174 dBm/Hz,最大天线增益和垂直旁瓣衰减设置为18 dBi和18 dB[11,13]。
5.1 测试函数下QBFO与二分法寻优性能分析
为了进一步说明QBFO算法寻优的优越性,我们采用Shaffer’s F6函数来比较两种算法的寻优性能。

图4 Shaffer’s F6函数图Fig.4 Shaffer’s F6
Shaffer’s F6函数:
(24)
从图4可以看出该函数仅有一个全局最优解1,解点为(0,0)。我们规定当使用算法得到的最终寻优值大于0.9995,则该函数已找到收敛解。函数图如图5所示。

表1 QBFO vs二分法Tab.1 QBFO vs binary search
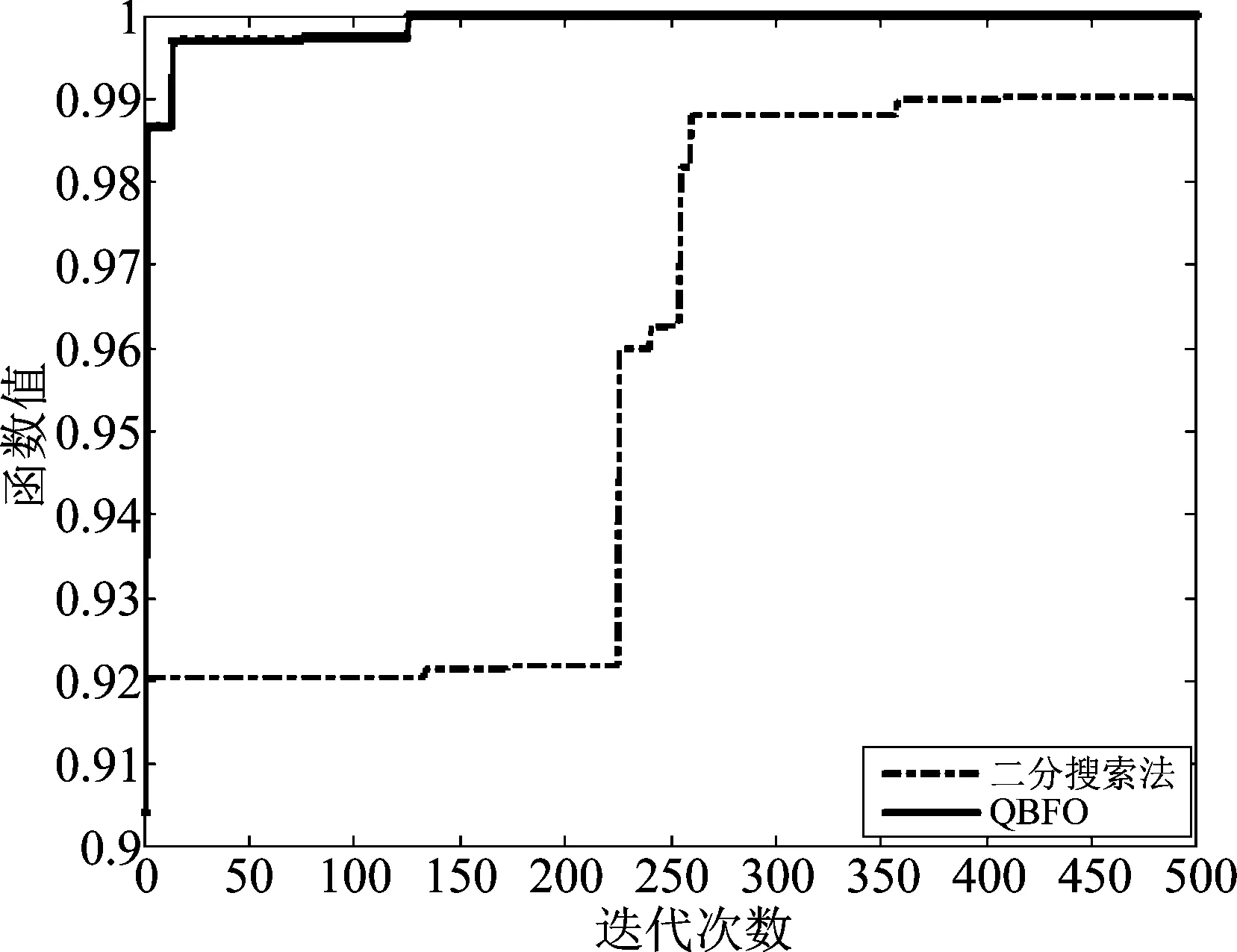
图5 两种算法寻优情况图Fig.5 Binary search vs QBFO
从图5以及表1可以看出,二分搜索法会陷入局部最优解,而QBFO算法不管是从收敛代数还是寻优终值都是优于二分搜索法的。
5.2 目标函数下各算法的仿真分析
本节我们使用了文献[11]中的二分搜索法来比较MRT和ZF的性能,然后在目标函数下比较QBFO算法与二分搜索法寻优性能。图中“Simulation”表示蒙特卡罗仿真结果,“Approximation”表示公示(22)计算结果,Proposed Alg表示采用QBFO算法仿真结果。
图6和图7分别比较了在3D MIMO信道模型下,其他条件相同情况下随着发射功率增加或用户数量增加,采用MRT和ZF预编码的系统性能。
图6所示,如果用户的位置已知,那么在高SNR的情况下(基站发射功率大于40 dBm),采用MRT预编码的3D波束赋形技术和采用ZF预编码的3D波束赋形技术所获得的和速率趋于恒定;而在低SNR的情况,两种波束赋形技术所获得的和速率都随发射功率的增加而增加。从图中可以看出在低SNR的情况下,采用MRT预编码的3D波束赋形技术是优于采用ZF预编码的3D波束赋形技术的。
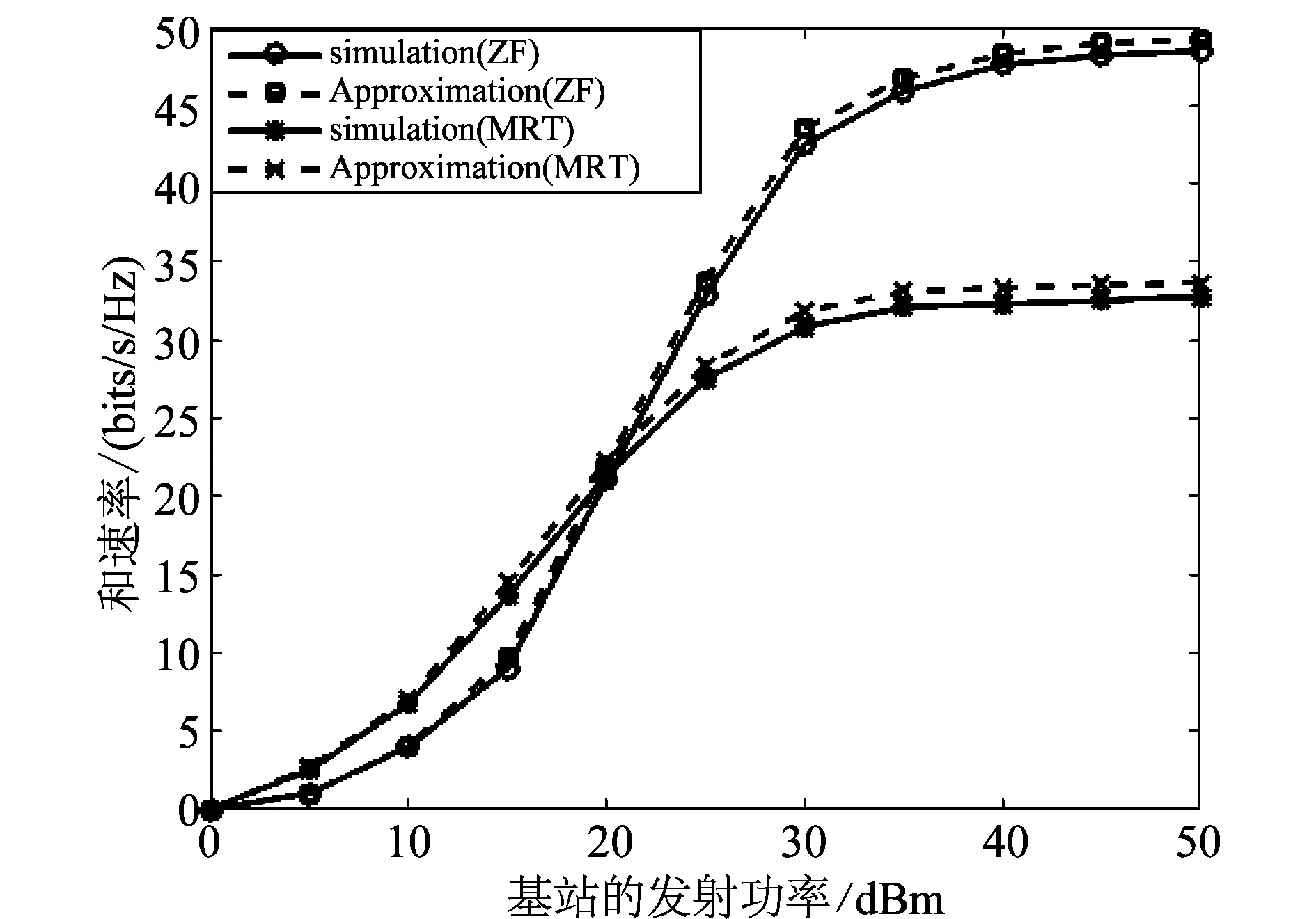
图6 基站发射功率对和速率的影响(Nt=32,K=8,Nr=1,d=250)Fig.6 Sum-rate vs. the transmit power(Nt=32,K=8,Nr=1,d=250)
图7所示,当天线数量和发射功率给定的情况下,采用ZF预编码的3D波束赋形技术是存在一个最优的服务用户的,在文献[13]关于这点做了详细分析。图7进一步说明了,在低SNR的情况下,采用MRT预编码的3D波束赋形技术是优于采用ZF预编码的3D波束赋形技术的。这里用户越多SNR越低[13]。
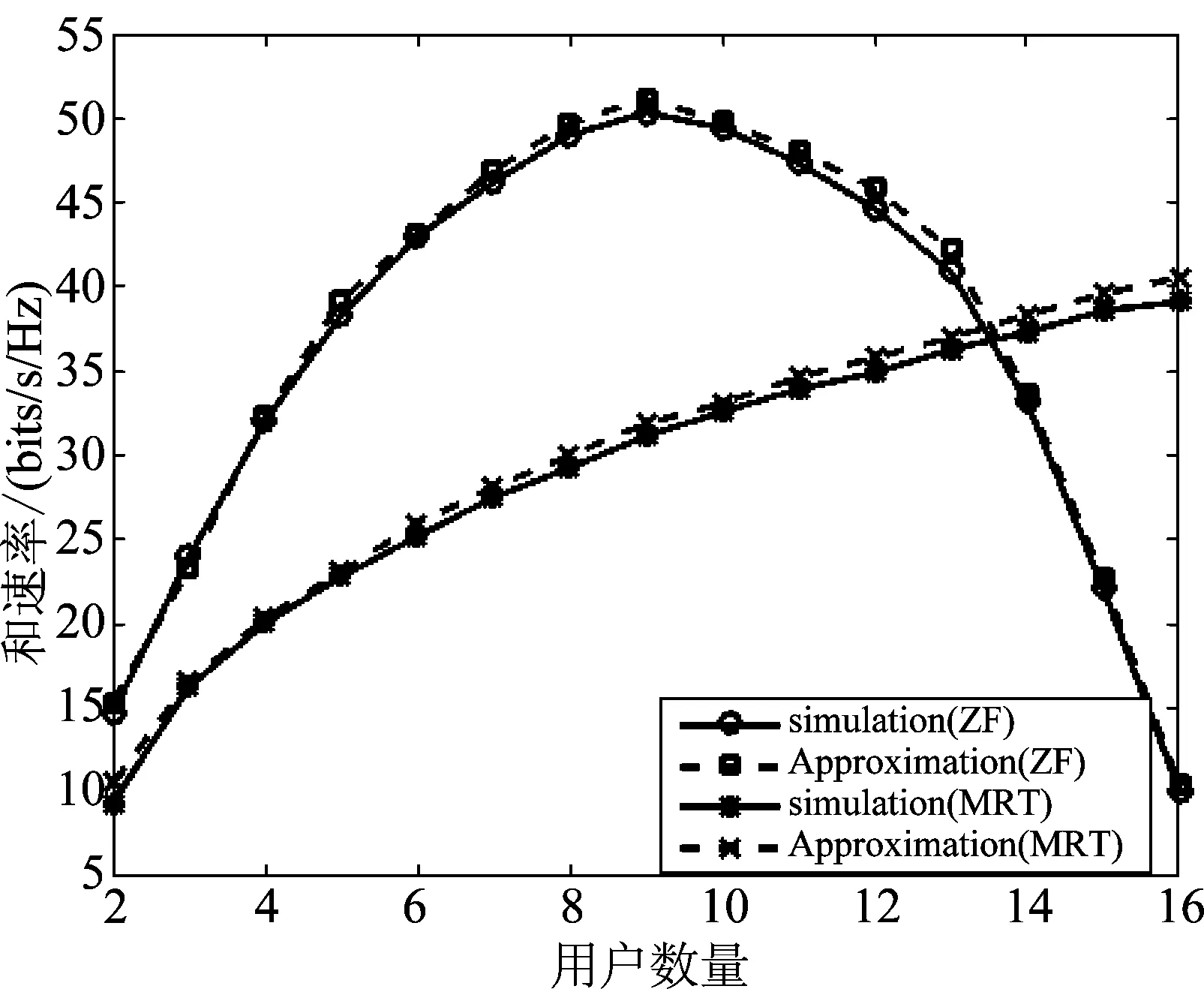
图7 用户数量对和速率的影响(Nt=32,Nr=1,Pt=43 dBm,d=250)Fig.7 Sum-rate vs. the number of users(Nt=32,Nr=1,Pt=43 dBm,d=250)
从图6和图7,可以看出在低信噪比或者有效用户更多的情况下,采用MRT预编码的3D波束赋形是优于采用ZF预编码的3D波束赋形的。图6中低信噪比指的是较低发射功率。
从图8可以看出,在高信噪比情况下,系统和速率趋于稳定。QBFO算法的寻优结果是优于二分搜索的。

图8 基站发射功率对和速率的影响(Nt=32,K=8,Nr=1,d=250)Fig.8 Sum-rate vs. the transmit power(Nt=32,K=8,Nr=1,d=250)
图9分析了用户数量与系统和速率的关系,可以看出QBFO性能优于二分搜索法。
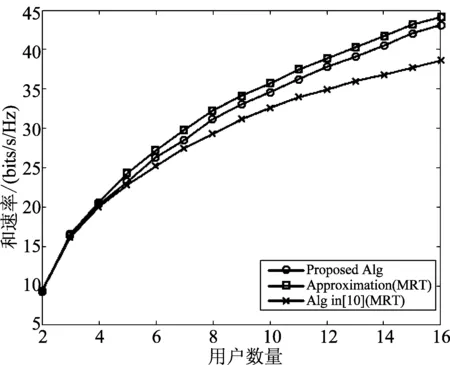
图9 用户数量对和速率的影响(Nt=32,Nr=1,Pt=43 dBm,d=250)Fig.9 Sum-rate vs. the number of users(Nt=32,Nr=1,Pt=43 dBm,d=250)
从图8与图9可以得出,与传统算法相比,QBFO算法性能优越,可以避免陷入局部最优解,并且图5进一步验证了QBFO算法的优越性。
6 结论
本文分析了在下行链路蜂窝网场景基于MRT预编码的垂直波束赋形来对系统和速率进行的优化方案,并且优化了天线下倾角,使得系统和速率最大化。本文使用了伽马分布推导了和速率的近似解,并且根据这个结论,比较了采用MRT预编码的3D波束赋形技术和采用ZF预编码的3D波束赋形技术的适用场景。本文主要考虑垂直维度的波束增益,创新性的采用QBFO算法寻找最优下倾角的方法来抑制小区间多用户干扰的方案,性能优于传统二分搜索法。
[1] Paulraj A J, Gore D A, Nabar R U, et al. An overview of MIMO communications-A key to gigabit wireless[J].Proc. IEEE, 2004, 92(2): 198-218.
[2] Catreux S, Driessen P F, Greenstein L J. Simulation results for an interference-limited multiple-input multiple-output(MIMO) cellular system[J]. IEEE Communications Letters, 2000, 11(4):334-336.
[3] 黄敏,缪蔚,周世东,等. MIMO系统中基于 TH 预编码的多用户空间复用方案[J]. 清华大学学报:自然科学版, 2008, 48(4): 514-517.
Huang Min, Miao Wei, Zhou Shidong, et al. TH precoding based multiuser spatial multiplexing scheme in MIMO systems[J]. Journal of Tsinghua University Science and Technology, 2008, 48(4): 514-517.(in Chinese)
[4] Jafar S A, Goldsmith A. Transmitter optimization and optimality of beamforming for multiple antenna systems[J]. IEEE Transactions on Wireless Communications, 2004, 4(3): 1165-1175.
[5] 白帆,李汀,李飞,等. 3D MIMO系统下水平和垂直维联合预编码的研究[J]. 信号处理, 2016, 32(9): 1093-1100.
Bai Fan, Li Ting, Li Fei, et al. Research on Joint Precoding of Horizontal and Vertical Dimension in 3D MIMO System[J]. Journal of Signal Processing, 2016, 32(9): 1093-1100.(in Chinese)
[6] Koppenborg J, Halbauer H, Saur S, et al. 3D beamforming trials with an active antenna array[C]∥in International ITG Workshop on Smart Antennas (WSA). Dresden Germany:IEEE, 2012: 110-114.
[7] Halbauer H, Saur S, Koppenborg J, et al. 3D beamforming: Performance improvement for cellular networks[J]. Bell Labs Technical Journal, 2013, 18(2): 37-56.
[8] Lee W, Lee S R, Kong H B, et al. 3D beamforming designsfor Single User MISO systems[C]∥in Global Communications Conference (GLO BECOM). Atlanta GA USA:IEEE, 2013: 3914-3919.
[9] Lee W, Lee S R, Kong H B, et al. Downlink vertical beamforming designs for active antenna systems[J]. IEEE Transactions on Communications, 2014, 62(6): 1897-1907.
[10] Muller A, Hoydis J, Couillet R, et al. Optimal 3D cell planning: A random matrix approach[C]∥in Global Communications Conference (GLOBECOM). Anaheim CA USA: IEEE, 2012: 4512- 4517.
[11] Fan Jiancun, Li G Y, Zhu Xiaolong. Vertical beamforming with downtilt optimization in downlink cellular networks[C]∥in Global Communications Conference (GLOBECOM). San Diego CA USA: IEEE, 2015: 1-5.
[12] Heath R W, Wu T, Kwon Y H, et al. Multiuser MIMO in Distributed Antenna Systems With Out-of-Cell Interference[J]. IEEE Transactions on Signal Processing, 2011, 59(10): 4885- 4899.
[13] Lim Y G, Chae C B, Caire G. Performance Analysis of Massive MIMO for Cell-Boundary Users[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6827- 6842.
[14] Xue Jinding, Jiang Shuai, Liang Yan, et al. Quantum Bacterial Foraging Optimization Based Sparse Channel Estimation for 3D MIMO Systems[C]∥In Wireless Communications & Singal Processing(WCSP). Yangzhou China:IEEE, 2016: 1-5.
[15] Passino K M. Biomimicry of bacterial foraging for distributed optimization and control[J]. IEEE Control Systems, 2002, 22(3): 52- 67.

