基于导频信号的LTE系统高移动性信道估计算法
王艳艳 韩 丰 瞿辉洋 陈 强 刘光辉
(电子科技大学信息与通信工程学院,四川成都 611731)
1 引言
自20世纪80年代以来,移动通信经过三十多年的迅速增长,已经成为连接人类社会的基础信息网络。随着第四代移动通信(Fourth Generation, 4G)[1-3]进入商用阶段,第五代移动通信(Fifth Generation, 5G)[4-5]成为全球研发的热点。综合考虑5G系统的技术需求、发展趋势以及网络平滑演进等因素,4G的平滑演进将是对下一代移动通信的有效补充。研究表明,未来通信系统将满足低时延,高可靠,大连接,高速移动等多样化场景的需求[6],这对系统的同步和信道估计等关键技术带来了严峻的挑战。尤其在高速移动环境下,设计高精度的信道估计算法成为研究的热点。在高速移动信道下(目前中国高铁的最大速度为350 km/h),由于较高的最大多普勒频移,正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统子载波间的正交性被破坏,产生严重的子载波间干扰。因此,需要设计一种信道估计方法来准确获取高速场景下的信道信息,并通过信道均衡消除多径信道的影响。
信道估计算法根据是否用到导频信息来划分,主要分为非盲信道估计[7-10]、半盲信道估计[11]和盲信道估计[12-13]。相对于盲信道估计和半盲信道估计,借助导频的非盲信道估计被大量采用,其优点是复杂度低、统计时间短、精度较高。
基于导频的信道估计方法主要分为两类:基于参数变换的信道估计(如基扩展模型(Basis Expansion Model, BEM))和基于插值的信道估计。BEM信道建模[14-15]是将信道的每一个时变抽头系数表示为一组基函数的加权叠加。它对高速移动信道建模的准确性更高,但其信道估计要基于分组的导频模式。这种导频模式在信道时延扩展严重时要求的导频数量很多,从而大大增加系统开销。然而,在LTE下行为离散导频模式,这极大地限制了基于BEM 的信道估计在LTE 下行OFDM 系统中的应用。LTE系统离散导频模式能较好的平衡导频开销、实现复杂度和信道估计精度之间的折中。基于离散导频的插值信道估计可以分成两个步骤[16-18]:第一步是估计导频处的信道频域响应(Channel Frequency Response, CFR),主要利用的估计方法为最小二乘(Least Square, LS),但是在高速移动信道下,由于多普勒频移较大,子载波之间正交性被破坏,使得LS的估计精度较低;第二步是通过导频处的CFR估计出数据处的信道值。维纳(Wiener)滤波算法[16]可取得理论上的最优估计,但要求已经信道的二阶统计特性,计算复杂度几乎不可实现。在广义平稳非相干散射信道假设条件下,为了降低计算复杂度,可将时频二维的内插简化为频域方向和时间方向级联的内插方法,其性能损失可以忽略。
在LTE系统中,传统的频域方向信道估计算法主要分为三种类型:(1)基于统计特征的内插算法:最小均方根误差算法[19](Minimum Mean Square Error, MMSE),其算法涉及矩阵求逆,复杂度较高。(2)基于固定系数的内插算法:线性内插、二阶高斯内插、三阶样条内插[20]、三阶拉格朗日内插。固定系数内插算法实现复杂度较低,但是若信道变化较快,固定系数内插器与信道失配,会降低信道估计精度。(3)基于低通滤波的内插算法:凯撒(Kaiser)[21]滤波内插算法和升余弦窗内插算法。这种算法性能介于MMSE和固定系数内插器之间。然后把频域方向估计的CFR作为已知值进行时间方向的信道估计。在LTE系统中,一般是基于一个子帧进行数据传输,由于时间方向一个子帧(14个OFDM符号)的导频个数较少,且不等间隔分布。传统的信道估计方法为线性内插[22-24],最后两个OFDM符号处的信道值需要线性外插。当多普勒频移较大时,线性信道估计算法精度降低,系统的性能变差,不能满足相对恶劣的信道传输环境。
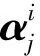
2 系统模型
LTE系统原理框图如图1所示。发送的二进制比特数据b进行信道编码得到信号c,然后把编码之后的信号c调制映射得到复数信号d。同时插入导频c1以进行信道估计,对导频信号调制映射得到导频处的复数信号d1。根据LTE系统的资源分配原理(如图2(a)所示),将调制映射之后的数据和导频映射到相应的位置,记为:Xd和Xp,其中导频信号的长度为Npilot。根据LTE系统资源元素映射之后的数据进行OFDM 调制(包括信号填零扩充,重排位置,逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)、添加循环前缀(Cyclic Prefix, CP))得到时域信号x,发射信号x经过无线信道得到信号y。

图1 LTE系统原理框图Fig.1 System model of the LTE


图2 LTE系统资源网格和导频结构图Fig.2 Resource grid and pilot scattering structurefor the LTE system
3 信道估计算法
在传统的信道估计算法中,时间方向信道估计算法为基于线性插值的估计,且最后两个OFDM符号处的CFR需要外插。但是在高速移动环境下,由于子载波之间的正交性被破坏,导频处CFR受到邻近子载波的干扰,且由于导频的非均匀分布,使得信道估计算法精度大大降低。因此,本文利用基于DFT的降噪算法提高导频处CFR的估计精度,并设计两种时间方向信道估计算法,内插出数据处的信道值,以提高系统性能。
图3为信道估计原理框图,其详细过程为:为了避免利用外插得到数据处的CFR,首先接收第一个子帧和下一个子帧第一个OFDM符号的信道值(如图2(a)所示),利用LS算法估计导频处的信道值;然后利用基于DFT的降噪算法提高导频处CFR的精度;根据降噪之后的CFR进行频域方向信道估计(如图2(b));最后进行时间方向的信道估计。时间方向信道估计算法为:1) 自适应的信道估计方案:数据处的CFR通过多个导频处的CFR值线性表示。由于导频间隔不同,线性表示所需系数通过最小均方误差准则计算得出,然后根据计算的系数估计出数据处CFR值。2) 把非均匀的导频结构转化为均匀的导频结构,再通过三阶样条内插算法进行信道估计。这种方法避免信道估计的外插,并利用更多的导频信息,提高了CFR精度。
3.1 基于DFT降噪的信道估计算法
为了抑制导频处高斯白噪声的影响,本文利用基于DFT的降噪算法[25],其基本思想为:把导频处的CFR进行逆傅里叶变换,去除最大时延位置之后的数据,最后再把截断之后的时域信道值变换到频域,以提高导频处的信道估计精度。根据发射端导频信号Xp和接收端导频处的信号值Yp,利用LS算法得到导频处的CFR,记为
(1)
把公式(1)得到的导频处的CFR通过逆傅里叶变换到时域,得到信道的时域冲激响应(Channel Impulse Response, CIR)为
(2)
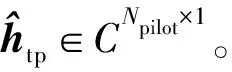
(3)
其中Ncp表示OFDM信号循环前缀的长度;⊗为两个向量各个元素点乘符号。为了保持CFR和CIR长度相同,把公式(3)补零,即
(4)
最后把(4)再变换到频域,可以得到去除噪声之后导频处的CFR值
(5)

图3 信道估计原理图Fig.3 The block diagram of the proposedchannel estimation methods
3.2 自适应的信道估计算法
传统的MMSE内插器系数计算公式[17]为
(6)

0≤u≤Qt-1,0≤ν≤Qt-1
(7)

由于时间方向导频不等间隔分布,不能直接利用公式(7)计算内插器系数。本文基于最小均方误差准则分别计算信道估计所需的内插系数,并可适应不同的导频间隔。若导频处的基于DFT降噪的信道估计和频域方向信道估计已经完成,则在时间方向估计数据处的CFR时,利用当前估计CFR值前后导频处CFR值的函数来表示。且信道的CFR自相关函数和子载波之间的间隔有关,和位置无关。

(8)


(9)
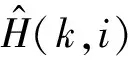
J(ω)=E{|e(i)|2}=E{e(i)e*(i)}
(10)
其中符号(·)*表示共轭。根据维纳霍夫方程Rω=p,可得到最优的内插系数方程为
ω=R-1p
(11)
其中R为已知CFR(导频处的CFR)的自相关值,p为当前估计CFR和已知CFR的互相关值。系数ω是由插值系数构成的矩阵。
(12)

(13)

(14)

图4 时间方向信道估计示意图Fig.4 Channel estimation procedure of the time direction
其中m和n表示四个导频处OFDM符号位置,若信道满足Jakes模型,则信道CFR的自相关函数为
r(x)=J0(2π|x|fDTs)
(15)
信道的互相关矩阵p中元素可表示为:
(16)
其中i-m的值表示各组的四个参考OFDM符号位置,i为各组中数据处的OFDM符号位置,若信道满足Jakes模型,则CFR的互相关函数为
p(x)=J0(2π|x|fDTs)
(17)
3.3 基于均匀导频结构的信道估计算法
自适应的信道估计算法通过最小均方误差准则计算信道内插估计所需的系数,这种算法相对于线性插值可提高CFR的精度,但是需要已知信号的统计特性。当信道的统计信息未知时,本文设计了一种基于三阶样条内插的算法。首先通过DFT降噪算法得到导频处的CFR,然后进行频域方向信道估计,最后时间方向信道估计。在进行时间方向信道估计时,把不等间隔的导频分布转化为等间隔的导频分布,利用三阶样条算法得到数据处的信道值。

(18)
H[k,mp]和H[k,mp-1]分别表示第k个子载波第mp和mp-1OFDM符号处(导频处)的信道值。然后把时间方向的OFDM符号分成两组(如图4(b)和(c)),每组分别进行三阶样条内插信道估计。设三次样条函数Si(x)在每个子区间[xi-1,xi]上的表达式为
Si(x)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3
(19)
其中ai,bi,ci,di为待定常数。根据插值条件和边界条件[26]可求得三阶样条的内插系数。相对于线性内插,基于三阶样条的内插算法信道估计精度提高。
4 计算复杂度分析
为了分析时间方向和导频处信道估计算法的计算复杂度,本文通过计算信道估计所需的乘法次数作为算法的计算复杂度。当未知信道的统计信息时,算法计算复杂度为:(a)LS算法的乘法次数为Np,其中Np为导频的个数;(b)基于DFT降噪的方法提高导频处信道估计精度,所需乘法次数为Nplog2Np;(c)通过公式(11)和(12)可知,当固定某个子载波,求解LTE系统一个子帧(14个OFDM符号)数据处的信道值时,需要求解由系数组成的矩阵ω。求解这个矩阵系数时,利用4个导频信息,基于最小均方误差准则求解。因此对于整个子载波N,算法的乘法次数为:2*43N;(d)当得到系数之后,根据(8)表示数据处的信道值,N个子载波的所需乘法次数为8*4N。因此对于未知信道统计特性的信道估计计算复杂度为:
Cs1=Np+Nplog2Np+128N+32N
(20)
当已知信道的统计信息时,所提算法的计算复杂度除了包含LS和降噪处理外,还包括把非均匀的导频间隔转化为均匀的导频间隔,并利用三阶样条算法计算数据处的信道值这个过程的计算复杂度,所需乘法次数为:2N+8*4N,其中N为所有子载波的个数。因此总的计算复杂度为
Cs2=Np+Nplog2Np+34N
(21)
同理对于LTE系统基于线性的信道估计算法,其乘法次数为:
Cs3=Np+Nplog2Np+10N
(22)
通过比较Cs1,Cs2,Cs3可知,虽然所提算法利用最小均方误差准则求解系数,但是由于LTE系统时间方向导频的个数比较少,所提算法的计算复杂度和基于线性的信道估计算法在同一个数量级上,其计算复杂度并没有大幅度提升。
5 仿真分析
为了分析不同内插器对不同多普勒大小的鲁棒性,图5比较了MMSE内插器、Kaiser内插器、线性内插器、升余弦内插器、二阶高斯内插器和三阶拉格朗日内插器多普勒域响应曲线。其中Kaiser内插器系数[18]的计算公式为
n=0,1,…,Nf-1
(23)
I0(x)为修正的0阶贝塞尔函数;Nf为奇数;且Nm=(Nf-1)/ 2;ξ为Kaiser窗成形系数;wc为截止频率。

图5 不同内插滤波器多普勒域响应比较Fig.5 Comparison of the different interpolation responsesin the Doppler domain
通过图5观察到,相对于固定系数内插方法(线性内插器、二阶高斯内插器和三阶拉格朗日内插器),MMSE内插器能很好的匹配不同的多普勒频移,可实现时间方向上的最佳信道内插,但需要已知信道的统计特性。固定系数内插方法不会随着信道多普勒频移的改变而改变,当多普勒频移变大时,固定系数内插器与变化无线信道统计特性的失配会降低信道估计精度,这不能满足高速移动条件下的LTE系统的需求。Kaiser内插算法的性能介于MMSE内插算法和固定系数内插算法,且不需要信道的统计特性。
在单天线模式,1/3 Turbo码率,16QAM调制方式,10 MHz带宽条件下,分别仿真理想信道估计和不同信道估计算法下的BER和均方误差(Mean Square Error, MSE)曲线,其详细仿真参数如表1所示。在仿真中,最大多普勒频移fd为300 Hz和1000 Hz,分别添加降噪算法和不添加降噪算法。假设LTE系统的载频频率f为2.4 GHz,则信道的移动速度为ν=fdc/f,其中c=3×108m/s为光速。若fd=300 Hz,信道的移动速度为135 km/h;若fd=1000 Hz,信道的移动速度为450 km/h。当已知信道的统计信息时,所用的信道估计算法为:频域方向基于MMSE 内插;时间方向自适应内插算法。当信道的统计特性未知时,所用的信道估计算法为:频域方向基于Kaiser 窗内插算法;时间方向基于三阶样条的内插算法。信道的MSE计算公式为
(24)
其中N和M分别表示子载波和OFDM符号采样点的个数。

表1 LTE系统仿真参数
图6和图7分别表示在添加降噪信道估计算法下和未添加降噪算法下不同信道估计算法的BER和MSE曲线。通过图6可知,在最大多普勒频移为300 Hz时,导频处加入降噪算法,且时间方向为自适应插值算法的BER性能优于其他信道估计算法得到的BER性能。时间方向为自适应插值算法的BER和理想信道估计的BER仅有0.5 dB(BER为10-4)的误差,优于线性插值算法。当未添加降噪算法时,其BER性能和理想信道估计算法相差约1.5 dB(BER为10-4)。因此,降噪信道估计算法提高了信道估计算法的性能,使得LTE信道估计性能提高。通过图7可得,频域方向基于MMSE的信道估计,时间方向为自适应的信道估计算法,且在导频处加入降噪信道估计算法的MSE性能优于其他信道估计算法。未加入降噪算法的MSE性能最差,进而得出降噪算法提高了信道估计精度。
当最大多普勒频移为1000 Hz时,在添加降噪和不添加降噪算法下,图8和图9分别展示了不同内插算法的BER和MSE曲线。通过图8可知,虽然频域方向基于FFT变换的信道估计算法[27]复杂度低,但是其BER性能差于时频两级级联的内插信道估计算法的性能。当系统利用一阶迫零均衡算法时,时间方向利用自适应信道估计算法的BER性能优于其他信道估计算法,和理想信道估计的BER约有1.2 dB(BER为10-4)的性能损失。由于信道的最大多普勒为1000 Hz,其子载波之间存在干扰,图8仿真了基于MMSE的子载波间干扰(Inter-carrier Interference, ICI)相消均衡[28]的BER曲线,可使得BER性能较一阶迫零均衡的性能略有提高。但是基于MMSE的ICI相消均衡算法要考虑多个子载波之间的影响,使得系统的计算复杂度很高。
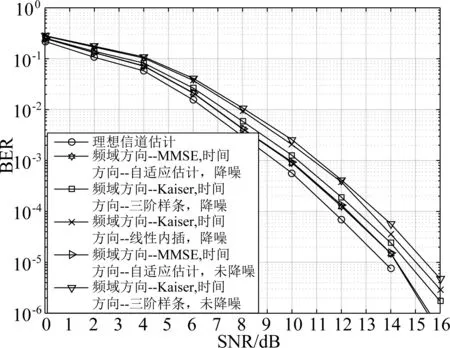
图6 双选择性衰落信道下,不同内插算法的BER比较(调制方式:16QAM,码率:1/3,Doppler:300 Hz)Fig.6 The BER performance of the OFDM with differentinterpolations over doubly selective fading channel(Modulation type: 16QAM,Code rate: 1/3, Doppler: 300 Hz)
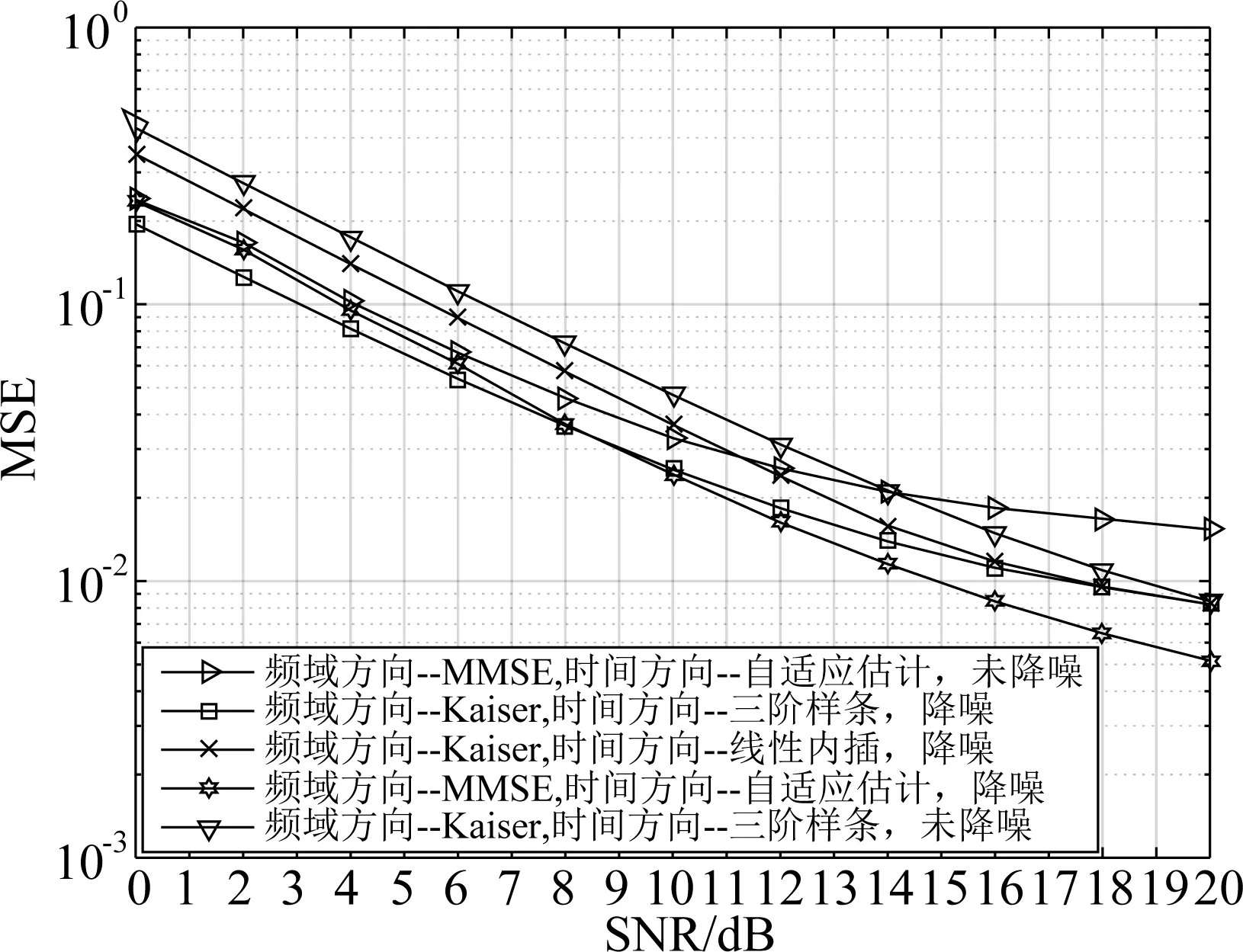
图7 双选择性衰落信道下,不同内插算法的MSE比较(调制方式:16QAM,码率:1/3,Doppler:300 Hz)Fig.7 The MSE performance of the OFDM with differentinterpolations over doubly selective fading channel(Modulation type: 16QAM,Code rate: 1/3, Doppler: 300 Hz)
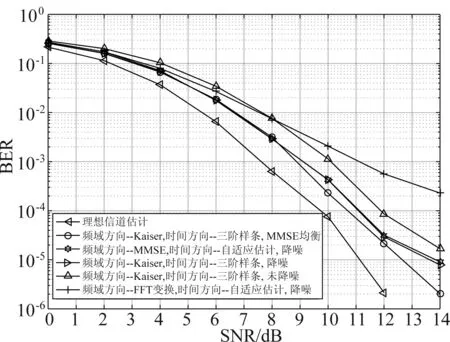
图8 双选择性衰落信道下,不同内插算法的BER比较(调制方式:16QAM,码率:1/3,Doppler:1000 Hz)Fig.8 The BER performance of the OFDM with differentinterpolations over doubly selective fading channel(Modulation type: 16QAM, Code rate: 1/3, Doppler: 1000 Hz)

图9 双选择性衰落信道下,不同内插算法的MSE比较(调制方式:16QAM,码率:1/3,Doppler:1000 Hz)Fig.9 The MSE performance of the OFDM with differentinterpolations over doubly selective fading channel(Modulation type: 16QAM, Code rate: 1/3, Doppler: 1000 Hz)
图9表示多普勒大小为1000 Hz下的不同信道估计算法下的MSE曲线。当频域方向为基于FFT变换的信道估计时,其MSE性能最差。在添加降噪算法前提下,频域方向为Kaiser的信道估计,时间方向为三阶样条内插信道估计的MSE性能最好。综上所述,本论文提出的自适应内插器可以利用更多的导频信息,且降噪算法提升了导频处的信道估计精度,进而更精确的估计高速移动信道值,提高系统的BER性能。
6 结论
本文针对LTE下行系统时间方向导频不等间隔分布的特性,提出了基于最小均方误差准则的自适应内插器和基于三阶样条的均匀内插器,以满足不同的导频间隔下的信道估计。这两种算法可利用更多导频的CFR信息估计数据处的信道值,而且可以避免外插,提高了系统的BER性能。仿真实验结果表明,本文提出的信道估计算法优于传统的线性插值算法。但是文中设计的信道估计还是基于插值的算法,对于超高速场景,由于子载波间干扰,这种算法的估计误差会变大。下一步的工作把自适应插值算法和最近的高速场景下的信道估计算法比较,并针对超高速信道场景对上述算法进一步改进或提出新的信道估计算法。
[1] Dong L, Zhao H, Chen Y, et al. Introduction on IMT-2020 5G Trials in China[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(8): 1849-1866.
[2] Khan F.LTE for 4G mobile broadband: air interface technologies and performance[M]. Cambridge: Cambridge University Press, 2009: 21- 68.
[3] Budomo J, Ahmad I, Habibi D, et al. 4G LTE-A systems at vehicular speeds: Performance evaluation[C]∥2017 International Conference on Information Networking (ICOIN). Da Nang, Vietnam: IEEE, 2017:321-326.
[4] Shafi M, Molisch A F, Smith P J, et al. 5G: A tutorial overview of standards, trials, challenges, deployment, and practice[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1201-1221.
[5] 尤肖虎, 潘志文, 高西奇, 等. 5G 移动通信发展趋势与若干关键技术[J]. 中国科学: 信息科学, 2014, 44(5): 551-563.
You Xiaohu, Pan Zhiwen, Gao Xiqi, et al. The 5G mobile communication: the development trends and its emerging key techniques[J]. Scientia Sinica Informationis, 2014, 44(5): 551-563.(in Chinese)
[6] Lien S Y, Shieh S L, Huang Y, et al. 5G New radio: waveform, frame structure, multiple access, and initial access[J]. IEEE Communications Magazine, 2017, 55(6): 64-71.
[7] Li Y, Cimini L J J, Sollenberger N R. Robust channel estimation for OFDM systems with rapid dispersive fading channels[J]. IEEE Transactions on Communications, 1998, 3(7):902-915.
[9] Mohammadian R, Amini A, Khalaj B H. Compressive sensing-based pilot design for sparse channel estimation in OFDM systems[J]. IEEE Communications Letters, 2017, 21(1): 4-7.
[10] 蒋琦, 赵春明, 贾鹏. OFDM系统基于导频的联合信道估计与干扰抵消算法[J]. 通信学报, 2007, 28(4):128-135.
Jiang Qi, Zhao Chunming, Jia Peng. Joint channel estimation and ICI cancellation algorithm for pilot-assisted OFDM systems[J]. Journal on Communication, 2007, 28(4):128-135.(in Chinese)
[11] Muquet B, De Courville M, Duhamel P. Subspace-based blind and semi-blind channel estimation for OFDM systems[J]. IEEE Transactions on Signal Processing, 2002, 50(7):1699-1712.
[12] Shin C, Heath R W, Powers E J. Blind Channel Estimation for MIMO-OFDM Systems[J]. IEEE Transactions on Vehicular Technology, 2007, 56(2):670- 685.
[13] 陈国军, 胡捍英. OFDM系统自适应盲信道估计新方法[J]. 信号处理, 2013, 29(6):777-781.
Chen Guojun, Hu Hanying. New blind adaptive channel estimation schemes based on OFDM systems[J]. Journal of Signal Processing,2013,29(6):777-781.(in Chinese)
[14] 高猛, 沈越泓, 屠佳, 等. 基于 DFT-BEM 模型的 LOFDM 系统双散射信道最大多普勒扩展估计[J]. 信号处理, 2012, 28(8): 1069-1076.
Gao Meng, Shen Yuehong, Tu Jia, et al. The maximum Doppler spread estimation based on DFT-BEM model for LOFDM systems in doubly-dispersive channels[J]. Signal Processing, 2012, 28(8): 1069-1076.(in Chinese)
[15] 李丹, 柯峰. 一种基于基扩展模型的 OFDM 频域快时变信道估计方法[J]. 信号处理, 2012, 28(2): 193-199.
Li Dan, Ke Feng. BEM based Frequency Domain fast Time Varying Channel Estimation method for OFDM Systems[J]. Signal Processing, 2012, 28(2): 193-199.(in Chinese)
[16] Hoeher P, Kaiser S, Robertson P. Two-dimensional pilot-symbol-aided channel estimation by Wiener filtering[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Munich, Germany: IEEE, April, 1997, 3(3):1845-1848.
[17] Dong X, Lu W, Soong A C K. Linear Interpolation in Pilot Symbol Assisted Channel Estimation for OFDM[J]. IEEE Transactions on Wireless Communications, 2007, 6(5):1910-1920.
[18] Liu G, Zeng L, Li H, et al. Adaptive Interpolation for Pilot-Aided Channel Estimator in OFDM System[J].IEEE Transactions on Broadcasting,2014,60(3):486- 498.
[19] Rossi P S, Müller R R, Edfors O. Linear MMSE estimation of time-frequency variant channels for MIMO-OFDM systems[J].Signal Processing,2011,91(5):1157-1167.
[20] Horowitz L. The effects of spline interpolation on power spectral density[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 2003, 22(1):22-27.
[21] Oppenheim A V, Schafer R W, Buck J R. Discrete-time signal processing[M]. Prentice-Hall, Inc. 1999.
[22] Takaoka S, Adachi F. Pilot-assisted adaptive interpolation channel estimation for OFDM signal reception[C]∥Vehicular Technology Conference.VTC 2004-Spring,2004,3:1777-1781.
[23] Hou X, Li S, Liu D, et al. On two-dimensional adaptive channel estimation in OFDM systems[C]∥Vehicular Technology Conference, 2004. Vtc2004-Fall. Los Angeles, CA, USA: IEEE, 2004, 1:498-502.
[24] 张皓彦. 基于3GPP LTE下行链路基带系统信道估计的研究[D]. 电子科技大学, 2012.
Zhang Haoyan. Study on the channel estimation of the 3GPP LTE downlink baseband system[D]. University of Electronic Science and Technology of China, 2012.(in Chinese)
[25] Van De Beek J J, Edfors O, Sandell M, et al. On Channel Estimation in OFDM Systems[C]∥Vehicular Technology Conference.Stockholm, Sweden: IEEE, 1995, 2: 815- 819.
[26] Durrleman S, Simon R. Flexible regression models with cubic splines[J]. Statistics in Medicine, 1989, 8(5): 551-561.
[27] Nguyen T T, Berscheid B, Nguyen H H, et al. A Novel Iterative OFDMA Channel Estimation Technique for DOCSIS 3.1 Uplink Channels[J]. IEEE Transactions on Broadcasting, 2017, 63(2):361-375.
[28] Liu G, Zhidkov S V, Li H, et al. Low-complexity iterative equalization for symbol-reconstruction-based OFDM receivers over doubly selective channels[J]. IEEE Transactions on Broadcasting, 2012, 58(3): 390- 400.

