一种基于低频水声传播特性的浅海地声参数反演方法研究

郑广学，祝捍皓，郑 红，林建民，汤云峰，朱 军

（浙江海洋大学海洋科学与技术学院,浙江舟山 316022）

浅海波导中，复杂海洋环境对声纳系统工作性能的限制一直以来是浅海水声工程应用所面临的挑战之一[1-4]。浅海中，声纳工作环境复杂多变，声信号传播时受海底、波导尺度及流体水文条件等因素的影响显著，而海底作为海洋波导中声传播的重要边界对信号传播的影响尤为明显，可靠的声传播建模和水声设备性能评估都需要已知海底的声学参数[5]。

现今，对海底参数的获取技术大体上可分为两大类[6]：一种是直接通过试验测量研究，包括试验场区现场测量和取样分析；另一类是通过声学方法反演获取。但两种直接测量法得到的往往仅是测量点的局部海底特性，由于浅海海洋环境复杂、多变，通过直接测量方法获得整个试验海区海底参数的时间、空间平均特性非常困难，而对测量声场的反演可替代大范围海域的直接测量，可快速、低成本地获取整个试验海区的底质参数，有着良好的发展前景。相比高频声波，低频声波由于波长较长，在浅海环境中受海底声学特性的影响更为显著且更易向远距离传播，因此利用低频水声信号大范围反演海底声学参数，受到了各国海洋科学研究者广泛的关注。

基于上述原因，本文针对浅海海底声速、声速衰减和密度三大类声学参数的反演问题展开研究，给出了一种基于低频水声传播特性的上述三类地声参数反演方法。并通过数值仿真与水池实验对本方法的可行性进行了分析、检验，以期为浅海海底地声参数的反演获取提供新思路。

1 反演方法概述

海洋环境参数的反演问题可系统性的概括为以下几个部分，即：参数化的海洋环境、声场正演模型、合理的目标函数、全局寻优算法和对结果的不确定性分析[7]，目前针对地声参数的反演研究、应用也仍是围绕上述各方向展开。在本文反演方法的研究过程中，也针对上述各部分进行了深入讨论和分析。

1.1 浅海声场正演模型

考虑浅海环境下，海底横波声速对低频声信号的传播影响不可忽略，为此本文研究中选择如图1所示的一类具有弹性海底的浅海参数化模型。建模中，令z=0位置代表海面，海面向下为深度z轴正值方向，r正轴表示声场向外传播方向；考虑在微小尺度范围内，海洋环境可用一组理想、近似平均参数表示，设参数化模型均匀流体层深度为H、密度ρ1、声速c1，声源位于海面以下深度zs处；海底为各向同性的半无限介质空间，纵波声速、横波声速、密度分别为 cp、cs和 ρb，αp和 αs分别代表纵波声速衰减和横波声速衰减，也是本文反演时的研究对象。

图1 具有弹性海底的浅海参数化模型Fig.1 A model with elastic bottom in shallow water

图1模型下，流体层中的各位置声压p(r,z)可表示为：

式中：ξ为水平波数；r为水平距离；J0为贝塞尔函数；A、B、C、β等参数的具体推导过程及表示式参见文献[7]。对于（1）式中声压场p(r,z)的数值计算，常用方法包括两种，一种是简正波方法，在ξ的复平面上利用留数定理对积分式进行求解；另一种是将积分式转化为傅里叶变换的形式进行求解，即为快速场方法[8]（Fast Field Method,FFM）。但当声源频率很低或海水深度很浅时，流体层中将激发其很少阶数的简正波，此时利用简正波方法求解得到的声场结果将存在一定的误差。在上述情况下，快速场方法将更加适合用于进行浅海声场的快速计算。

在本文研究中，为保证对声压场p(r,z)的计算精度及在反演过程中的效率要求，本文选择快速场方法实现对如图1所示参数化模型下声压场p(r,z)的数值计算。

1.2 目标函数与寻优算法

由于模型中海底声参数的变化会对声压场p(r,z)的分布产生重要影响[9]，因此通过建立衡量实测值p′(r,z)与理论预报值p(r,z)间适配的目标函数，通过对其的寻优求解可实现对图1模型下海底各参数的计算获取。基于统计学中的似然函数和最大似然理论[10]，本文给出在高斯数据误差假设下的衡量p′(r,z)与p(r,z)适配的目标函数如公式（2）所示：

其中，p′表示单个水听器在测量点（r,z）实际接收到的复声压（测量场）；m表示计算中待获取的多参数矩阵；B(m)表示归一化的Bartlett适配器，其表达式为：

（3）中上标“+”代表共轭转置，p(m)表征由快速场计算得到（r,z）处声压场的理论值。当且仅当传播距离上各测量点上p′与p(m)完全一致时，B(m)达到最优匹配，E(m)取到极小值；反之，E(m)取值越大。通过公式（2）和公式（3）的构造，将对海底参数的反演问题转化为在寻优范围内对公式（2）的极小值求解，利用各种寻优算法对（2）式求解可得到参数矩阵m中各参数值。

针对公式（2）建立的目标函数，本文研究中选用模拟退火（Simulated Annealing,SA）算法对其参数矩阵m中各海底参数值进行寻优求解，并通过对寻优最后一代结果分布和真值对比的讨论，分析本文所研究方法的可靠性。

2 仿真分析

为验证本文所研究地声参数反演方法的可行性与可靠性，本节利用数值模拟，通过对浅海声场正演模型与反演结果的仿真分析，对上述方法展开讨论。

2.1 声传播特性分析

利用FFM，图2首先给出了图1所示典型浅海环境下，100 Hz声信号在1～1 500 m范围内p(r,z)随传播距离变化的仿真结果，以传播损失（TL：Transmission Loss）的形式给出，TL曲线计算公式如（4）所示[11]：

仿真中设声源位于水下zs=20 m深度处，接收点z位于水下z=10 m处，传播距离r=1～1 500 m，仿真时采用的海洋环境参数如表1所示，图2（A）-图2（E）中实线对应表1中真值参数计算结果，点线与虚线分别对应五项海底地声参数取讨论值时的计算结果。图2（F）结合距平给出了在五项海底地声参数讨论值区间内，各参数变化时对TL曲线的影响程度，计算中以真值计算得出的TL值视为均值，以讨论值计算得出的TL值视为离散数据计算距平。

表1 海洋环境仿真参数Tab.1 The simulation parameters of ocean environment

从图2（A）-图2（E）的对比中可以看出，在其它仿真条件不变的前提下，改变任一海底声参数，均会使传播距离上各点的p(r,z)在数值上产生变化，这将为p(r,z)应用于海底参数获取提供了重要依据。但五项海底参数变化时对声信号传播特性产生影响的程度存在差异：当cp、cs取值改变时，TL曲线的波动最明显；其次为当ρb取值变化时，TL曲线变化起伏相对较明显；当αp、αs取值变化时，TL曲线变化起伏最不明显。从图2（F）中可以看出，五项海底参数的讨论值在真值偏移+10%的条件下，对TL的影响程度从大到小依次为 cp、cs、ρb、αp、αs；在真值偏移-10%的条件下，对 TL 的影响程度从大到小依次为 cs、cp、ρb、αp、αs。因此，五项海底参数对 p(r,z)的影响程度可初步定性为：cp、cs>ρb>αp、αs。

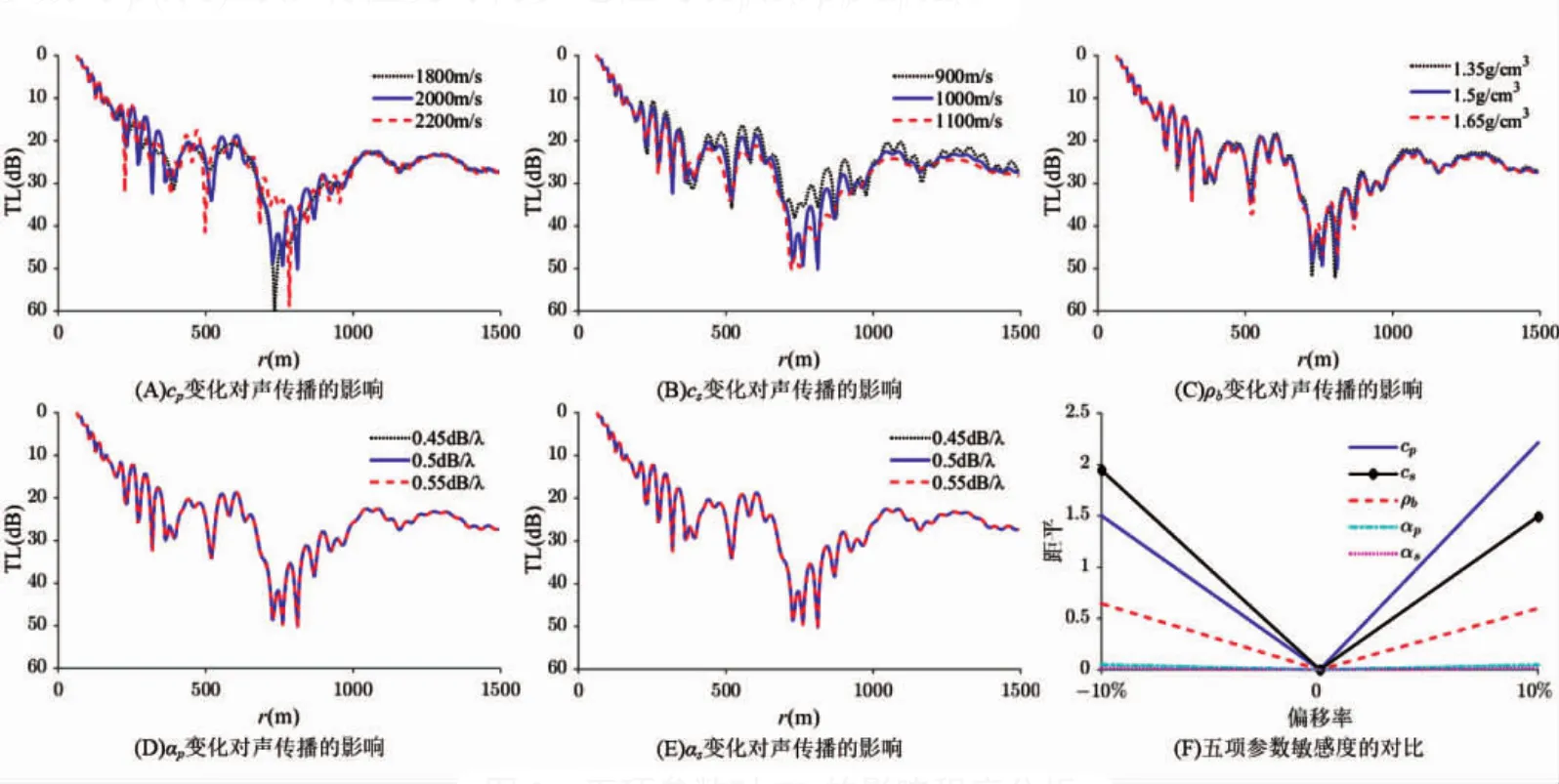
图2 五项参数对TL的影响程度分析Fig.2 The impact of five parameters on transmission loss

2.2 目标函数敏感度分析

在实现对浅海环境下单频声场计算的基础上，本节通过数值仿真讨论本文选定目标函数对所研究五项海底参数在变化时的敏感度，分析本文所选定目标函数在反演中的可靠性。仿真中，设声源频率f0作用下，环境参数真值下模拟计算得到p(r,z)为参考真值；讨论目标函数对某一海底声学参数的敏感度时，固定其它参数，只在所关心范围内变化该声学参数计算得到比较值p′(r,z)，由公式（2）计算p(r,z)与p′(r,z)间的目标函数值E(m)作为敏感度评价标准。理论上，当且仅当p(r,z)=p′(r,z)时，E(m)取得极小值，即对应仿真环境参数真值。

按以上处理方法，图3首先给出了在图1所示海洋环境下，当传播距离、声源频率、声源深度和接收深度不变时，由p(r,z)与p′(r,z)构造的目标函数E(m)随五项地声参数变化时的数值变化。研究中，仿真海洋环境参数真值如表1给出，令该环境下声源频率100 Hz、声源与接收深度分别为20 m和10 m，传播距离r=1～1 500 m条件下计算得到的p(r,z)为参考真值，五项海底声学参数的讨论区间分别为：（A）cp=1 800～2 200 m/s；（B）cs=900～1 100 m/s；（C）ρb=1.35～1.65 g/cm3；（D）αp=0.45～0.55 dB/λ；αs=0.45～0.55 dB/λ。。从图3的仿真结果可以看到，在所讨论参数区间内，目标函数E(m)均只在参数真值处形成尖锐极小值峰，且无伪峰或第二极小值，可以避免局部最优解对目标函数在后续算法寻优中的影响。但E(m)在五项海底声参数变化时波动范围不尽相同：其中随着cp、cs取值的变化，E(m)值的波动范围在-36～-6 dB区间内；ρ取值的变化对目标函数波动的影响次之，E(m)在-40～-12 dB区间内波动；而E(m)对αp、αs在讨论范围内的变化敏感程度相对较差，波动范围在-40～-15 dB区间内。图3（F）给出了五项参数敏感度的对比情况，E(m)值变化范围从大到小依次为 cp、cs、ρb、αp、αs。从 E(m)值变化范围分析，五项海底参数对 p(r,z)的影响程度可定性为：cp>cs>ρb>αp>αs，进一步细化了图 2 的讨论结果。

在图3的研究基础上，图4给出了五项海底地声参数在上述取值范围内，目标函数值E(m)在（cp、cs、ρb、αp、αs）两两组合影响下的二维分布图，目的是反映本文所选定目标函数对任意两类地声参数组合影响的分辨能力，目标函数值E(m)取值的峰值分布、偏向表现了其对所讨论两参数的敏感程度。

从仿真结果看：除图 4（C）、（D）、（F）、（G）、（I）图中出现纵向“斜峰”外，其余各图均只在表 1 中的仿真真值位置出现尖锐峰值，且二维平面上其余位置E(m)值与峰值相比存在较大差距，不易在寻优过程中造成干扰；而上述（C）、（D）、（F）、（G）、（I）图分别对应纵波声速衰减 αp和横波声速衰减 αs与其它参数的组合讨论结果，从中可以看到，相比其余几类参数E(m)对横、纵波衰减的敏感度相对较弱，这也与图2、图3的讨论结果一致。

图3、图4的研究结果表明，本文所选定的目标函数对所研究五项地声参数体现出了较高的分辨能力，将其应用于反演研究中，理论上避免陷入非真值处的局部最优解，同时能较好区分各类海底声参数对声传播的耦合影响，适用于本文中的反演研究。

图3 单参数敏感度Fig.3 The sensitivity of single parameter

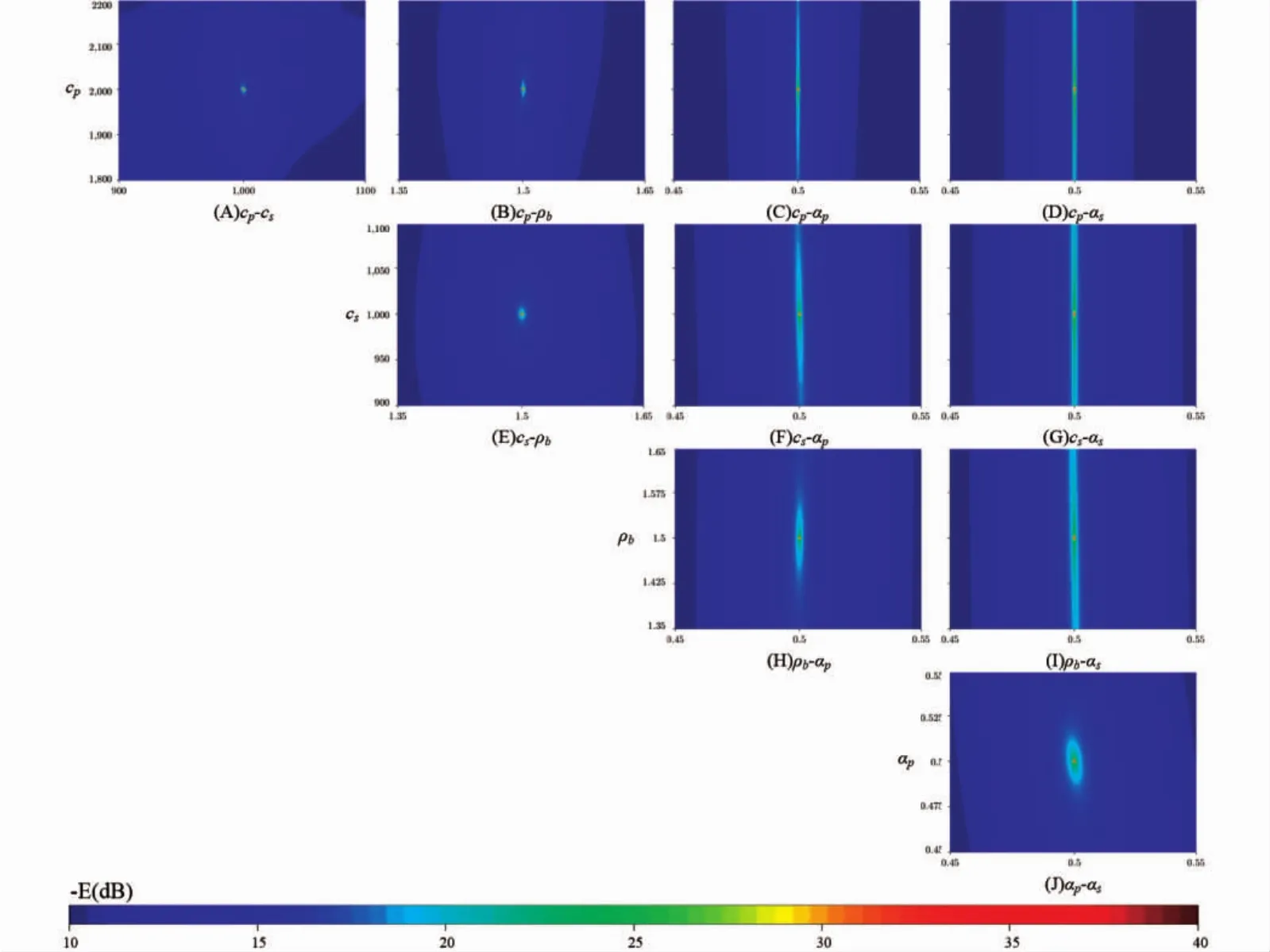
图4 两参数间敏感度Fig.4 The sensitivity between two parameters

2.3 反演结果分析

在完成对目标函数敏感度讨论的基础上，本节通过数值模拟，讨论寻优算法下对目标函数的寻优结果，通过给出仿真真值与寻优结果的误差对比，进一步分析本文所研究反演方法的可行性与可靠性。仿真中设声源位于水下zs=20 m深度处，接收点z位于水下z=10 m处，传播距离r=1～1 500 m，仿真测量场p′(r,z)计算时采用的海洋环境参数仍取表1中数值。

表2列出了数值模拟中设定的五项地声参数的仿真真值和利用模拟退火算法寻优时设定的各参数的搜索范围，最终搜索结果及其与设定真值的误差。在SA算法中，设定初始温度为100℃，每次执行迭代时的降温系数为0.99，算法终止温度为0.001℃，算法终止时共迭代1 147次。从表2可以看出，对于本文所建立的目标函数利用SA算法寻优得到的结果与真值误差基本一致，其中海底横波衰减αs寻优结果与真值相差最大，但也不超过2.2%。

表2 寻优结果Tab.2 The results of optimization

图5 仿真结果Fig.5 The simulation results

从图5可以看出，SA算法在寻优求解过程中，搜寻到的最后一代五项海底参数在搜索区间内的概率分布及在寻优过程中目标函数E(m)随寻优代数的数值变化，图5（A）-图5（E）的纵坐标P表示对应参数最后一代的概率（下同）。从图5（A）-图5（E）中可以看出，当寻优算法结束时，待反演五项参数均分别趋向某一稳定值，证明了表2中寻优结果的稳定性，且该值均处于仿真真值附近；图5（F）中，随着搜索代数的增加，目标函数E(m)在算法结束前已经处于平稳状态，从另一方面证明了本次计算结果的稳定性和可靠性，使得表2给出的反演结论更具有说服力。图6的对比结果也显示，利用寻优结果计算得到的理论声场p(r,z)与仿真测量声场p′(r,z)在传播距离上的分布特征也完全一致，证明了本文反演方法的可靠性。

图6 仿真结果验证Fig.6 The validation of simulation results

3 实验验证

在以上仿真分析的基础上，本节结合消声水池缩比实验[12]，利用实验数据对本文所研究反演方法进行讨论。实验中选取硬度高、质地均匀、耐磨性好的塑料板模拟“半无限弹性海底”；实验中将发射换能器固定于一端水中；接收水听器固定于带有光栅尺的精确移动平台上；根据发射换能器的频响特性，实验过程中发射信号中心频率为135 kHz的CW脉冲信号。

图7 实验装置示意图Fig.7 Setup of the experiments

表3给出了实验中各参数的测量结果，其中水中声速c1由测量水中温度（11.15℃）后通过经验公式[11]求得。测量过程中，保持声源位置固定，发射中心频率为135 kHz的CW信号（如图8（A）所示）；水听器固定于可移动走架上，设置采集卡采样率fs=20 MHz，每个测量点重复测量10次，避免随机扰动带来的影响；完成一点测量后，走架带动水听器向远离声源方向移动2 mm（误差不超过20 μm）；图8（B）给出了测量中所接收到的第50～150道接收信号时域图，图中各条线段是由表3中布放参数计算得到的、第50～150接收点上直达信号、水面反射信号和水底反射信号的达到时间。从图8（B）中可以看到，理论计算得到的各路径信号到达时间与实测达到时间基本吻合，证明了测量中接收信号的可靠性；图8（C）给出了实验过程中测得的传播损失曲线。

表3 实验参数Tab.3 The experiment parameters

图8 实验信号Fig.8 The signal in experiment

表4列出了基于实测135 kHz声压场p′(r,z)，利用本文所研究的反演方法得到“海底”地声参数，包括：五项参数的搜寻范围以及寻优的结果：

表4 寻优结果Tab.4 The results of optimization

如图9所示，SA算法在对水池实验数据寻优求解过程中，搜寻到的最后一代五项海底参数在搜索区间内的概率分布以及在寻优过程中目标函数E(m)随寻优代数的数值变化。结合表2与图9的结果可以看到，本方法在处理此次实测数据时，随着迭代次数的增加，如图9（F）所示目标函数E(m)在算法结束前也已处于平稳状态，证明了该目标函数在对实验数据的反演中依然保持了良好的收敛性；同时从图9（A）-图9（E）中可以看出，SA寻优过程最后一代各参数分布亦趋于某一稳定值，证明寻优结果达到稳态；更值得一提的是，在水池实验中选取的塑料板密度在购置时已知为1.2 g/cm3左右，这与对海底密度ρb寻优所得到的数值1.210 9 g/cm3仅仅相差0.91%，验证了本次反演结果的正确性，也更进一步证明了本文所研究反演方法的可行性和可靠性。

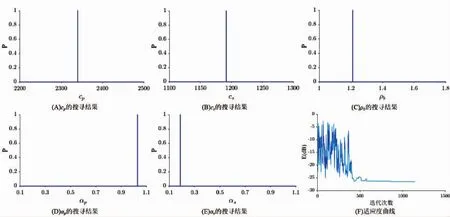
图9 反演结果Fig.9 The inversion results

如图10所示，利用表4寻优结果计算得到的传播损失曲线与实验中测得的传播损失曲线对比图。从图10的对比中可以看到，在各测量点(r,z)上，理论计算p(r,z)与实测p′(r,z)均吻合较好，再次证明了本次反演所得结果的有效性。

5 结论

本文研究了一种基于低频水声传播特性的浅海地声参数反演算法，并通过数值模拟和水池仿真实验，对本反演方法的可行性和应用前景进行了讨论。研究结果表明，在本文所给出的衡量实测值p′(r,z)与理论预报值p(r,z)间适配的目标函数下，应用以模拟退火为代表的寻优算法，可以准确反演海底地声参数值，理论仿真与水池实验结果均验证了本反演方法的有效性。

但本文研究结果仍存在一些不足。如，研究中只讨论了单频点声压场在反演中应用，忽略了海底地声参数值随频率变化的影响；其次，仿真及水池实验环境均过于理想，没有考虑海水中各类噪声对声场分布的影响；且对反演结果的讨论过于单一。针对以上不足之处，在后续的研究中，考虑通过加入了随机噪声，结合贝叶斯理论改进寻优结果等手段，进一步优化、改进本反演方法。

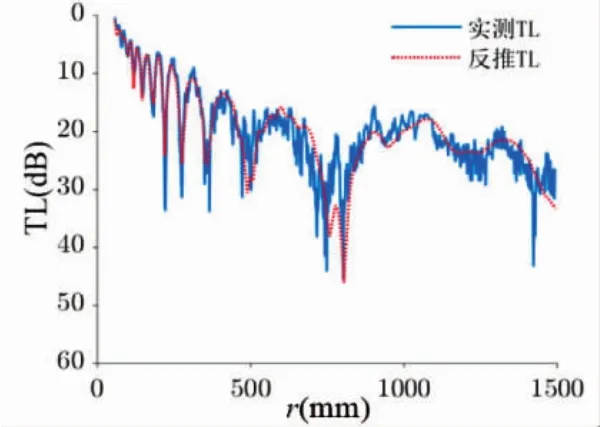
图10 反演结果验证Fig.10 The validation of inversion results