日字形薄壁杆件解析解与数值解对比分析

陈彪来

（甘肃交通职业技术学院，甘肃 兰州 730070）

0 引言

在工程实际中薄壁杆件受扭状态普遍存在，薄壁杆件虽然有部分特性类似于实体杆件，但对其进行力学性能分析时，横截面的翘曲变形不再是次要因素而忽略不计。因此由薄壁杆件组成的薄壁结构，无论从薄壁杆件自身还是薄壁结构整体来讲，其受力反应和变形都十分突出，必须对其分析。薄壁杆件力学的解析理论主要有不考虑截面外形轮廓线变形的乌曼斯基的闭口薄壁杆件的约束扭转理论和符拉索夫的广义坐标法，可以通过这些理论对薄壁杆件进行分析计算得到解析解，但其公式烦琐，推导复杂。而有限元方法由于其强大的实用性，可以较精确地考虑各种复杂形状和各种复杂的边界条件，因而成为研究最多、应用最广的数值方法。因而可以通过解析解与数值解的比较分析误差产生的原因，验证薄壁杆件在荷载作用下受翘曲效应的影响，并且得到有限元单元类型选择的相关原则。

1 多室闭合薄壁杆件解析解计算

1.1 竖向荷载作用下的弯曲正应力

如图1所示为薄壁杆件自由端截面图，坐标原点在对称中心处。因为其关于x轴和y轴对称，所以它的形心、主极点、弯曲中心、剪切中心都与对称中心重合。将竖向力往形心简化可以得到剪力Qy和扭矩T，如图2所示。

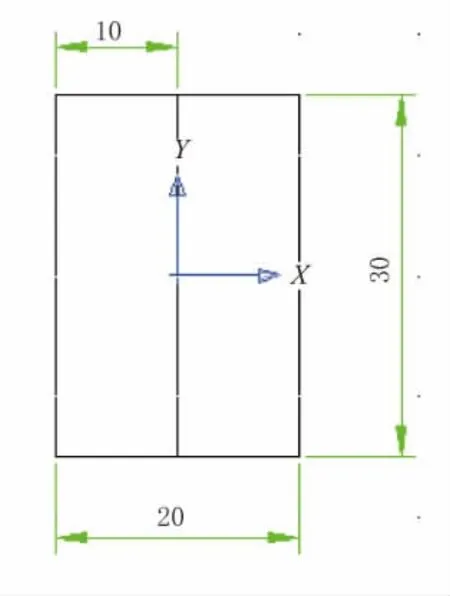
图1 截面中线图（单位：cm）

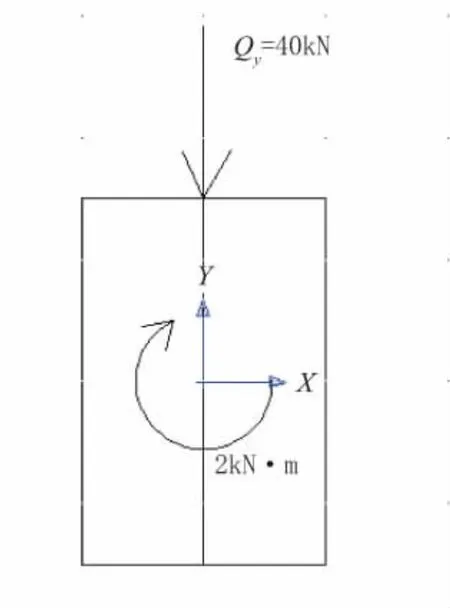
图2 竖向力向形心简化

根据材料力学：

则

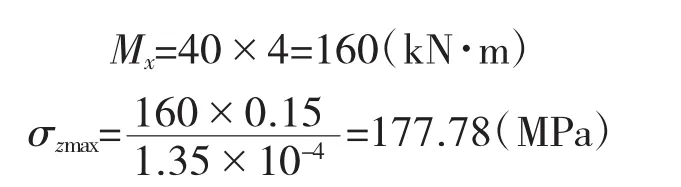
1.2 轴力作用下的弯曲正应力

偏心力向形心简化可以得到一个轴向拉力和两个弯矩Mx和My，如图3和图4所示。

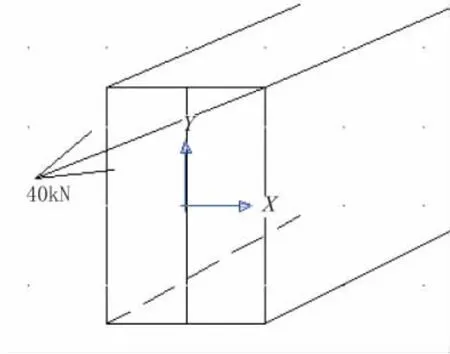
图3 模型轴向拉力作用位置图

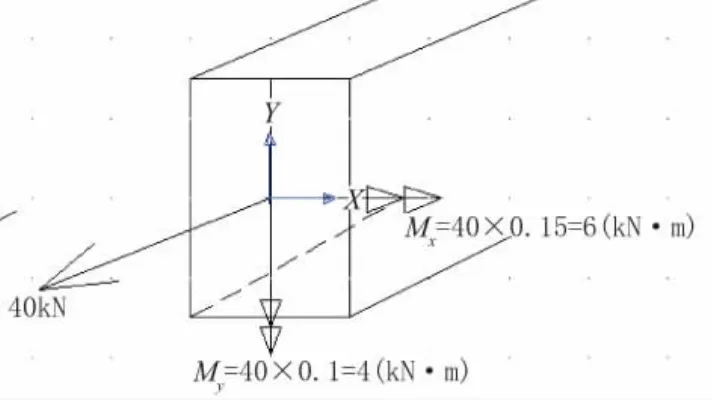
图4 轴向拉力向形心简化后等效荷载作用位置图

由上述弯矩作用的方向可以得到截面右上角点处最大的正应力：

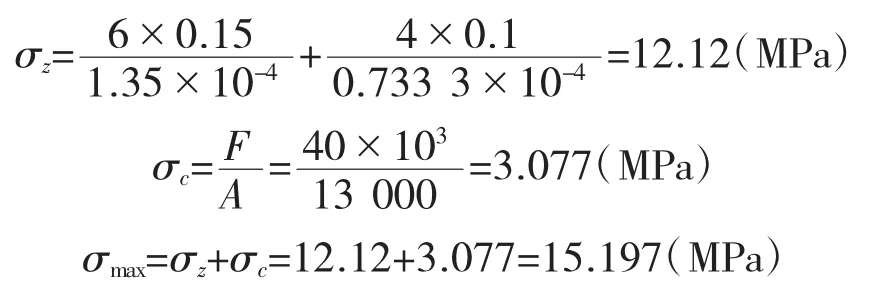
如图5所示，根据薄壁杆件理论首先在各室分别设置一个切口，将两个切口分别取在1点的左侧和右侧，在截面的各节点处给以标号，剪力流q0i表示节点i处的静定剪力流。应用公式计算时，由各切口处开始，依次计算各节点处的剪力流，显然在切口处q0i为零。

1室各点处的静定剪力流：

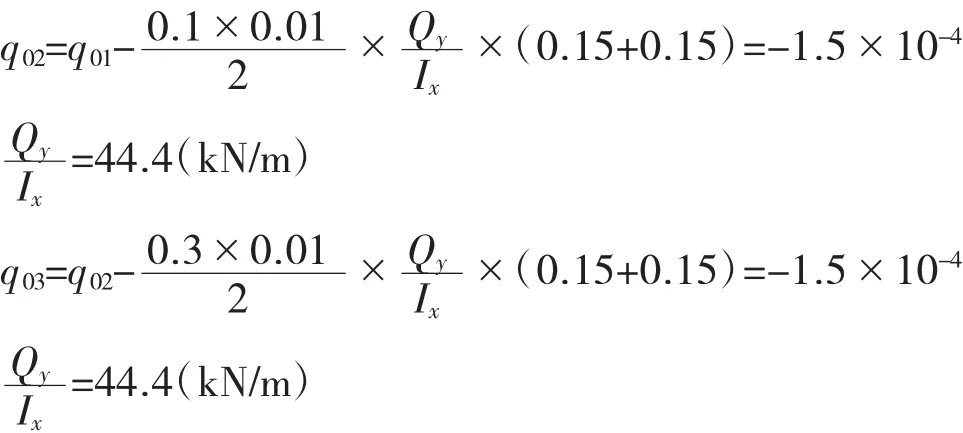
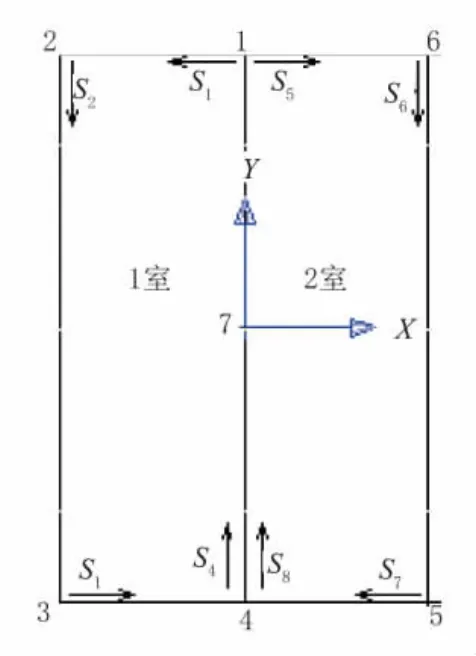
图5 多室闭合薄壁杆件弯曲剪应

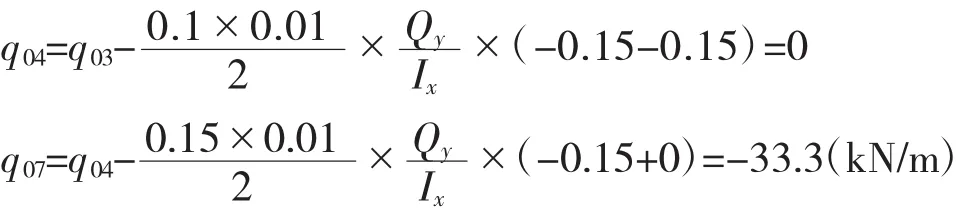
根据对称性，2室各节点处截面静定剪力流与1室对称节点处剪力流相等。

为了求解超静定剪力流qi（i=1，2，3，4，…，n），需依公式建立二元一次方程组。利用以下公式计算各室各板上的积分值：

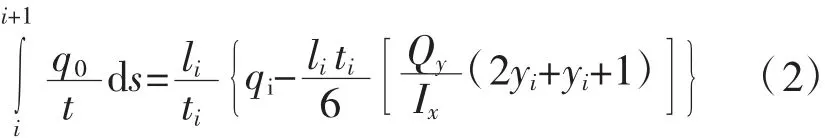
可通过下面的方程组求出两个附加剪力流q1、q2：

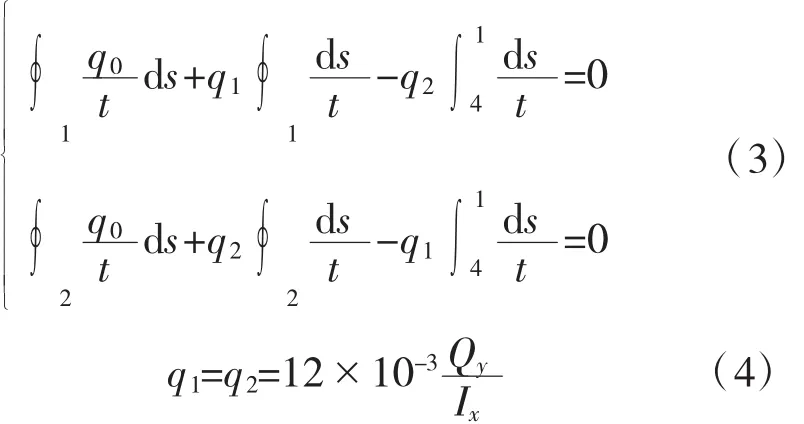
解得：

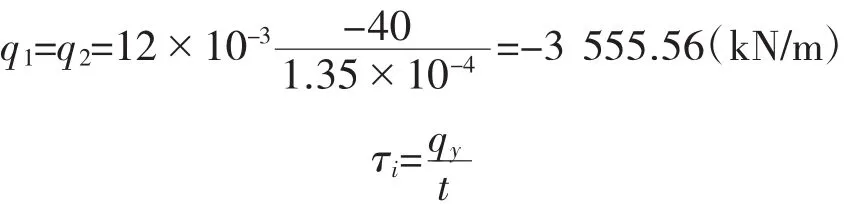
剪应力分布如图6～图8所示。

1.3 多室闭合薄壁杆件的自由扭转分析

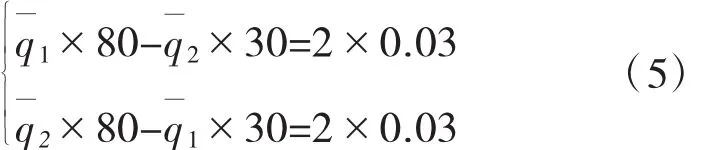
解得：

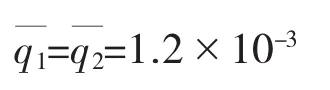
扭转惯性矩：It=2×（1.2×10-3×0.03×2）=1.44×10-4（m4）

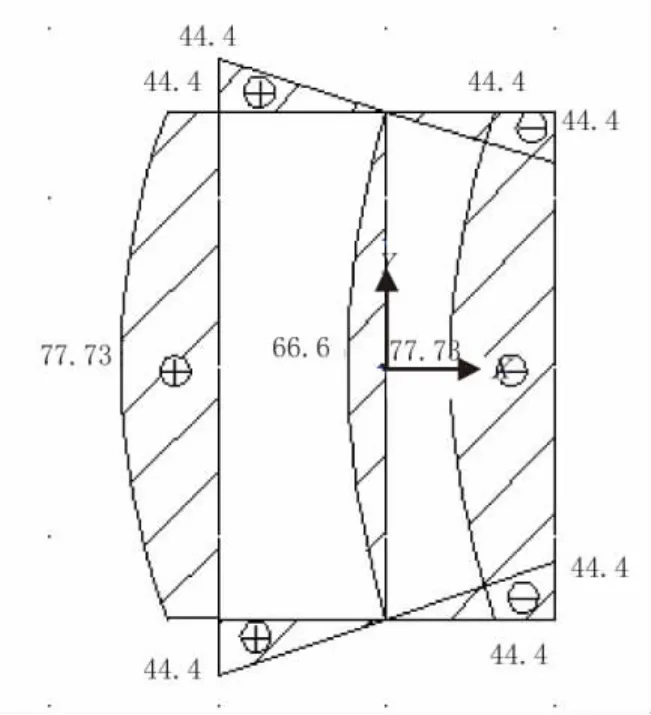
图6 q0分布图（单位：kN/m）

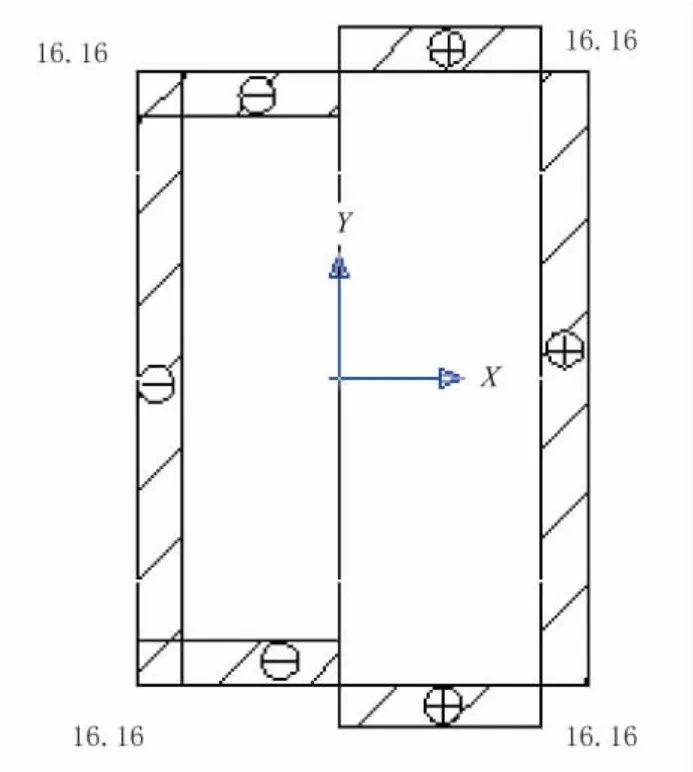
图7 qi分布图（单位：kN/m）

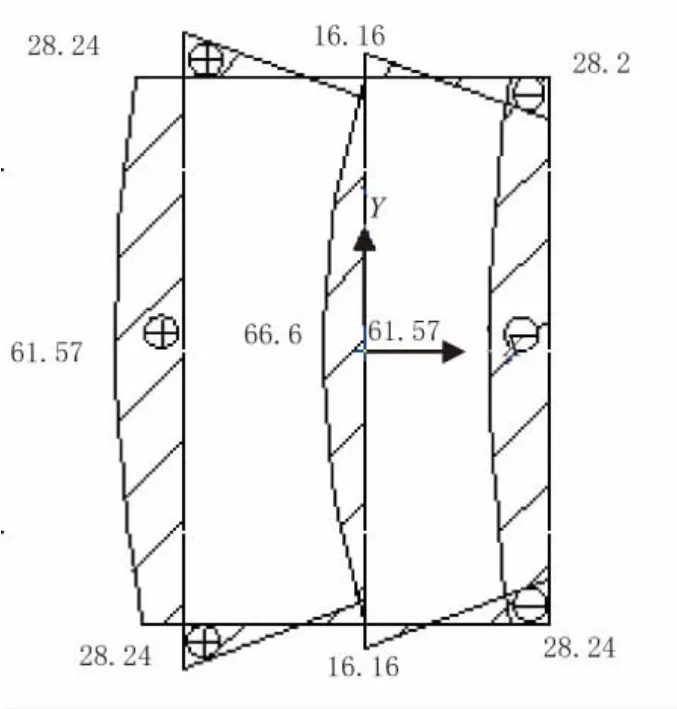
图8 q分布图（单位：kN/m）

利用公式（6），可求得各室自由扭转剪力流：

薄壁杆件悬臂梁在自由端竖向力作用下产生扭矩 Mt=-40×0.05=-2（kN·m），可得：

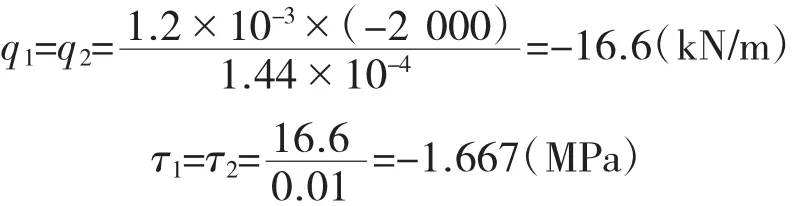
故截面剪应力顺时针转,其分布如图9所示。

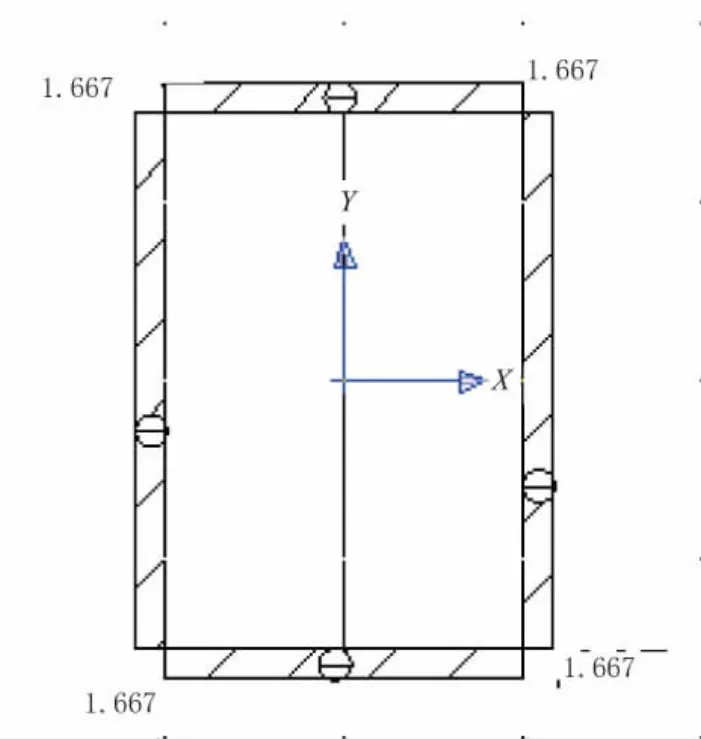
图9 τ分布图（单位：MPa）

1.4 多室闭合薄壁杆件约束扭转

根据截面中线图可得极惯性矩：

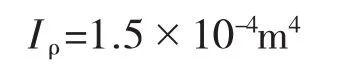
由此得修正系数:

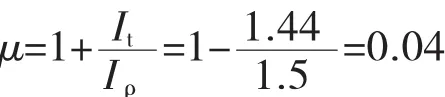
特征常数：

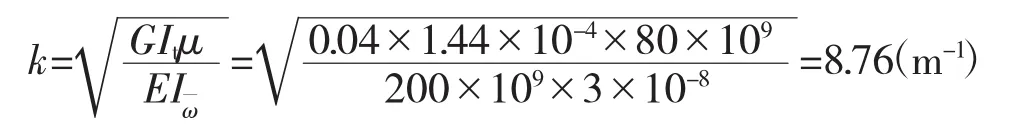
根据闭口薄壁杆件加载情况，得到约束扭转微分方程：

根据加载情况，将竖向力与轴力分开求解微分方程。

1.4.1 竖向力作用下边界条件

固定端：

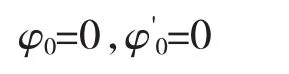
自由端：

由以上边界条件可得杆件双力矩函数和弯扭力矩函数：

由双力矩和弯扭力矩函数可计算固定端处的正应力：

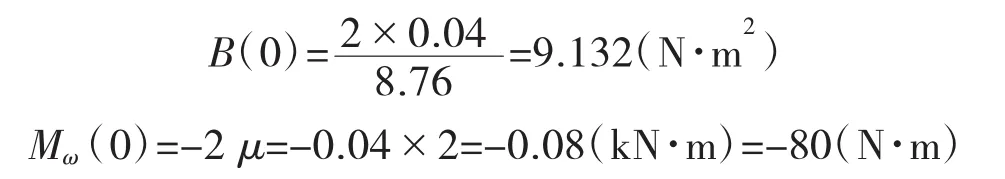
翘曲正应力：

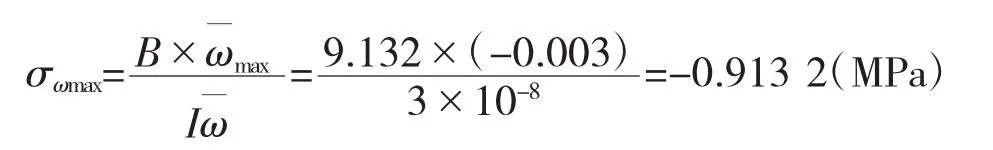
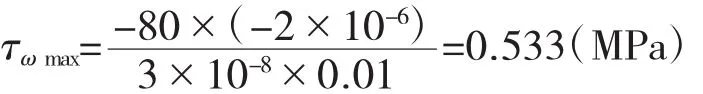
自由端：

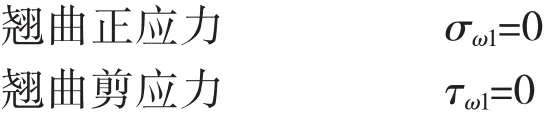
1.4.2 轴向力作用下边界条件

固定端：

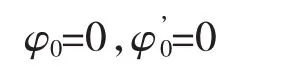
自由端：

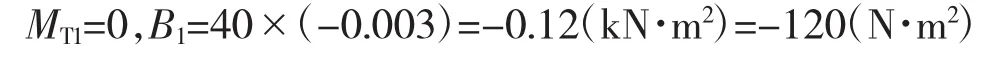
由以上边界条件可得杆件双力矩函数和弯扭力矩函数：

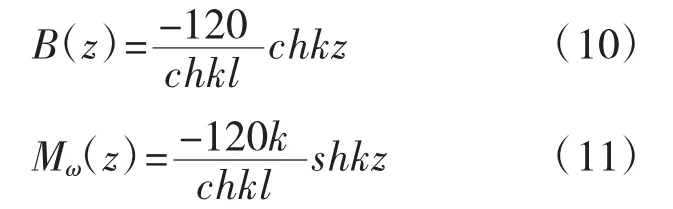
翘曲剪应力：

由双力矩和弯扭力矩函数可计算固定端处的正应力：

固定端：

2 多室闭合薄壁杆件数值解计算

2.1 竖向力弯曲正应力数值解

利用ANSYS建模进行数值解计算，在竖向力作用下弯曲正应力数值解与解析解分布相同，其正应力分布关于水平轴呈反对称分布，上边缘为正，下边缘为负。在角点处由于集中效应的影响，其正应力远比解析解数值要大。角点处的正应力值为284.09 MPa，模型中线角点处的数值解为204 MPa。因为剪切滞后效应的影响，ANSYS数值解分布图上下板的正应力不是均匀分布，在三块腹板上也不再是线性分布。剪切滞后是由于剪切变形造成应力分布不均匀的现象，此时靠近节点处的腹板不再符合平截面假定，应力增大。

2.2 竖向弯曲剪应力数值解

模型横截面上在各板的中间远离角点的地方，剪应力分布比较均匀，且应力值不是很大。而在角点处存在局部应力集中的现象，这些点处的剪应力值会急剧增大，比其他各点处的值要大9～10倍。

2.3 竖向力作用整体分析

在偏心的竖向力作用下，结构会受到横力弯曲、竖向剪力及扭矩的作用，所以截面上的应力包括弯曲正应力、弯曲剪应力、扭转剪应力、翘曲剪应力、翘曲正应力。总正应力和总剪应力为各项的线性叠加。下面来分析薄壁杆件解析解中的翘曲效应对薄壁杆件的影响。

固定端右上角点最大正应力：

σ=σz+σω=177.78-0.913 2=176.867（MPa）

固定端右腹板最大剪应力：

τ=τw+τk+τω=1.54+1.667+0.467=3.674（MPa）

从上述解析解结果可以看出，翘曲正应力占总应力的0.913 2/176.867=0.52%，扭转剪应力占总应力的2.134/3.674=58.1%。

2.3.1 正应力数值解比较

单元结点22830处的总正应力值是159.92 MPa,与解析解数值176.867 MPa比较，其误差为9.6%。从2.1节的ANSYS计算结点22838数值解中,弯曲正应力为284.09 MPa,总正应力为283.84 MPa，所以固定端右上角点处的翘曲正应力是σω=283.84-284.09=-0.25（MPa），其翘曲正应力数值解与解析解相比，误差为72.6%，误差比较大。数值解的翘曲正应力0.25 MPa占总正应力283.84 MPa的比例约为0.09%，这一数值与解析解相比差别不大。

2.3.2 剪应力数值解比较

单元结点91325处的总剪应力值是3.378 MPa，从2.1节ANSYS计算的结点91325处数值解中,弯曲剪应力为1.120 4MPa，所以右腹板中间处的扭转剪应力是 τn=3.378-1.102 4=2.275 6（MPa），其自由扭转剪应力数值解与解析解十分接近，误差为13.7%。数值解的扭转剪应力2.275 6 MPa占总剪应力3.378 MPa的比例约为60.7%，这也与解析解的比值接近。

3 两种求解方法比较及原因分析

（1）闭口薄壁杆件在此假定基础上，运用薄壁杆件理论计算公式，计算约束扭转剪应力及约束扭转正应力。但是在用ANSYS计算闭口薄壁杆件时，运算过程中不会考虑到平截面假定。由上述分析可知，薄壁杆件解析解理论不考虑截面外形轮廓线的变形，这与实际情况是不符的。而用有限元软件ANSYS进行数值计算反映了截面轮廓线的变形，所以两者产生了较大的误差。

（2）剪力滞后效应会使ANSYS数值解在界面边缘的值不均匀，使得角点处的最大值远大于解析解。如在第2节ANSYS数值解与解析解的比较中，由于横力弯曲所引起的固定端正应力在上下板上应该是均匀分布的，但是从ANSYS数值解计算图中可以看出在上下顶板上应力分布是不均匀的，特别是靠近节点板处，在腹板和顶板的交界处最大，随着离开节点距离的增大而逐渐减小，因此正应力的横向分布呈曲线形状，使得顶、底板的中间小而两边大的分布状态，使得弯曲正应力呈现不均匀分布的现象。

（3）局部集中效应会导致最大值出现在集中力作用点处，以及在腹板与顶、底板的交界处出现最大值。由于集中效应所造成的应力最大值与按薄壁杆件理论求得的解析解最大值有极大的误差，所以比较力的作用点处的值是没有意义的。根据圣维南原理，在远离力的作用点处的应力值可以应用等效荷载去求解，其与理论求解结果是相吻合的。在力的作用截面上，由于薄壁杆件的厚度较小，在截面上按照圣维南原理受到集中荷载的影响较大，其用ANSYS计算的数值解与理论解析解的误差也是相当大的。

4 结语

（1）用实体对闭口薄壁杆件建立有限元模型，可以很好地得出正应力及剪应力在截面上的分布情况，而且与用薄壁杆件理论得到的解析解分布相当吻合，如图10和图11所示。

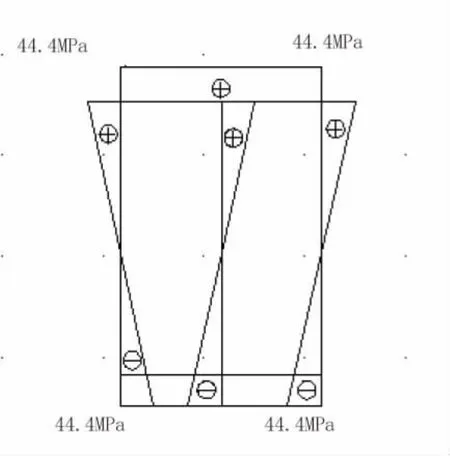
图10 数值解与解析解吻合

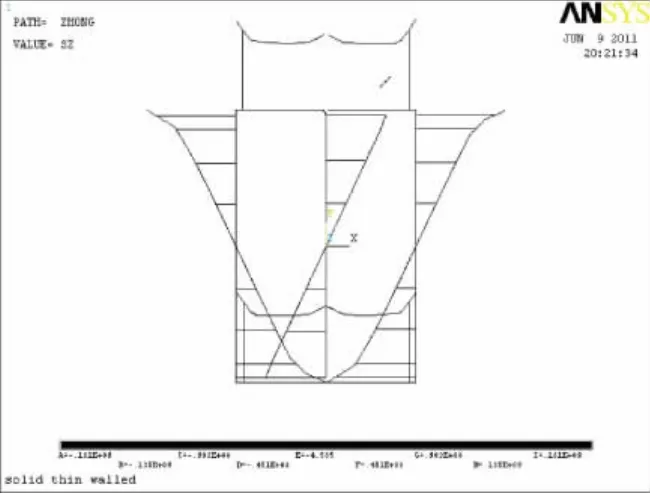
图11 ANSYS计算模型

在角点处有集中效应、剪切滞后效应现象出现，所以在角点处的应力比数值解要大得多，应力分布也不是线性分布。由于壳单元在处理上与实体单元存在差异，尤其是在角点处得到的数值解与解析解十分接近，误差不会超过10%。以竖向力的横力弯曲为例，解析解在有角点处的数值为44.4 MPa，用壳单元分析得到的数值解是45.698 MPa,两者误差仅为2.9%,是相当吻合的。

（2）对于两种荷载（竖向力、轴力）下的闭口薄壁杆件的翘曲效应不一样，在轴力作用下自由端的翘曲效应比较大。解析解得到的翘曲正应力占到了66.2%,用实体分析得到的结果是57.2%，用壳单元分析得到的结果是50.4%，两种翘曲正应力数值解所占比例都小于解析解结果。由于在集中荷载作用面上会有应力集中,圣维南原理不适用，所得到的总应力比实际情况偏大，并不是简单的线性叠加。