基于晶振特征的重点雷达信号快速靶向识别

朱永成， 潘继飞， 沈家煌， 金天祥， 刘 鑫

(国防科技大学电子对抗学院，合肥 230037)

0 引言

目前，常规的雷达信号分选参数包括载频(RF)、到达角度(DOA)、脉宽(PW)以及脉冲重复间隔(PRI)等参数，选取合理的分选参数，才能从混叠的脉冲序列中分选出某部雷达信号的脉冲。然而，随着雷达技术的快速发展，频率捷变、重频抖动、捷变信号的应用已成为现在雷达的标配，尤其对于多功能雷达来说，参数往往是交叠的，另外，脉冲丢失现象常见以及会有几部同型号的雷达同时工作，导致利用传统的分选参数难以快速有效分选识别出雷达信号。因此，寻找分选识别效果更佳的参数以及开发新的算法，完成对雷达信号的快速识别具有一定的实际意义。对文献[1-3]进行分析，证明了晶振特征可以作为识别雷达信号的一个重要的特征参数，还需要进一步验证利用晶振特征识别重点雷达目标信号的效果。因此，提出利用雷达晶振参数的重点雷达信号快速识别算法。

1 多功能雷达的PRI生成原理

1.1 脉冲信号的生成原理

多功能雷达信号的脉冲流主要是由利用频率合成技术的主振放大式发射机产生的，如图1所示。

图1 采用频率合成技术的主振放大式发射机原理图Fig.1 Schematic diagram of the main vibrator transmitter using frequency synthesis techniques

雷达时钟信号(基准振荡频率)由基准频率振荡器(晶体振荡器)中的石英晶体振荡频率产生，脉冲信号的载频由基准振荡频率经过倍频器和混频器产生，PRI由基准振荡频率经过分频器产生。因此，RF和PRI可以认为是由石英晶体振荡频率产生的。

1.2 PRI建模

PRI产生的原理如图2所示。

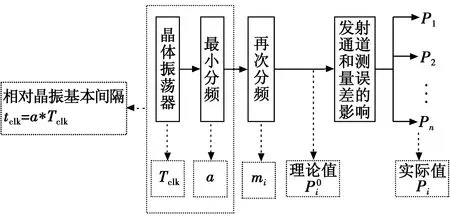
图2 PRI产生的原理图Fig.2 Schematic diagram of PRI

因此PRI可表示为

(1)

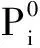
从式(1)可以看出，利用晶振特征完成对重点雷达信号的识别，高精度PRI测量是前提。文献[4]中的方法可以成功应用于纳秒量级精度的雷达PRI测量，文献[5]中的方法对时间间隔的测量精度可以达到10 ps量级。现有的PRI高精度测量技术满足本文的实际需求，通过以上对各参数量级的分析，对PRI的测量误差一般可以忽略不计。

2 基于晶振特征的重点雷达信号快速靶向识别的处理流程

处理流程如图3所示，采用并行的数据处理方式，多个并行处理器同时利用不同的晶振特征对混叠的脉冲进行处理，每部重点雷达信号的快速识别与其他的雷达信号是否识别没有关系。无需对脉冲流进行大量的运算，每个支路只需运行识别与某一部重点雷达信号有关的运算。

图3 快速靶向识别的处理流程Fig.3 Rapid targeting recognition process

2.1 基于晶振特征的重点雷达信号快速靶向识别算法的基本原理

依据多功能雷达PRI生成的原理分析可知，PRI是由晶振基本间隔经过分频产生的，则式(1)可简要表示为

Pi=mia×Tclk+Δεi=(mi+Δεi/aTclk)×aTclk=(mi+bi)×aTclk

(2)

bi=Δεi/aTclk

(3)

式中：mi是由分频电路产生的，为整数；Δεi的数量级远小于aTclk；bi的值接近于零。经过以上分析可知，对接收信号的脉冲流进行处理，若该脉冲流中含有某重点雷达信号，则脉冲流中将有一定数量的PRI和该雷达的相对晶振基本间隔接近整除；若全脉冲中不含有该雷达信号，则不具有该性质。

2.2 基于相对晶振基本间隔的重点雷达信号快速识别算法

将脉冲流中两个脉冲的到达时间相减，并以此间隔除以重点雷达信号的相对晶振基本间隔，记录连续整除的脉冲数。若连续整除的次数达不到设定的要求，则以其他的时间间隔继续进行以上步骤，直到满足条件的时间间隔都进行了相关处理为止；若没有脉冲符合条件，则认为脉冲流中没有重点雷达信号。具体算法如图4所示。

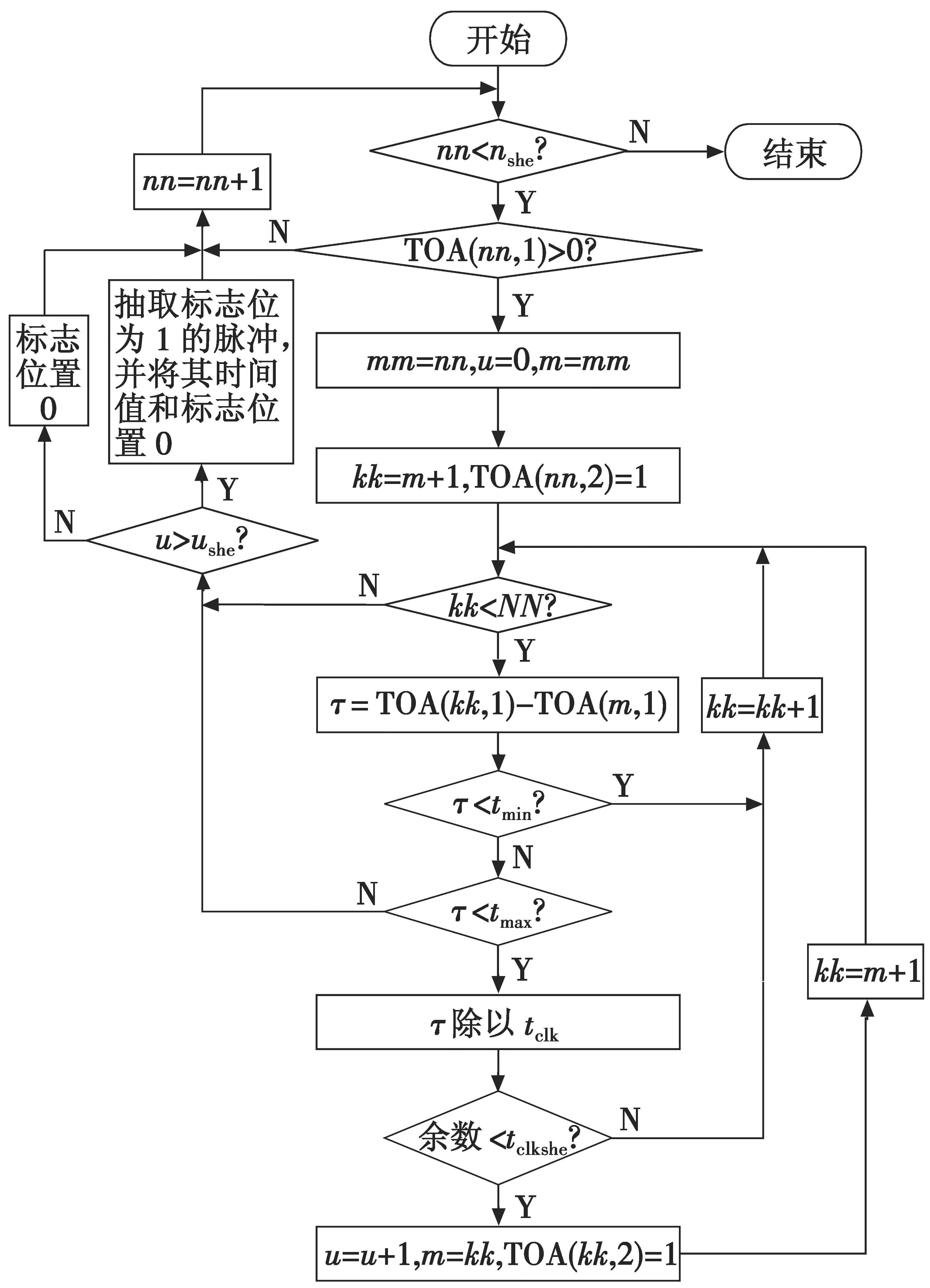
图4 基于相对脉冲基本间隔的重点雷达信号快速识别Fig.4 Rapid identification of key radar signals based on the basic interval of the relative pulse

图中：τ表示两个脉冲的时间差值；nshe为预先设置的一个数。相对脉冲时间间隔在tmin和tmax之间，有大于ushe个连续脉冲时间间隔可以整除tclk，则认为脉冲流中有重点雷达信号，tclk为相对晶振基本间隔，若余数小于门限值tclkshe,则认为τ可以整除tclk。

2.3 进一步识别重点雷达信号的工作状态

随着雷达技术的快速发展，多功能雷达的发展已然成为趋势，且符合实际需求。多功能雷达是可以同时执行搜索、多目标跟踪、导弹制导等多种工作任务的雷达。对多功能雷达的工作任务进行分析，每种工作任务需要相应的工作模式来完成。在不同的工作模式中参数是捷变的，多部同型号雷达的工作参数是相互交叉的。例如载频，同一个区域多部同型号多功能雷达的载频变化范围出现重叠，为避免雷达之间的相互干扰，某雷达在某工作模式下，采用的具体载频点是不同的。

3 计算机仿真分析

本文利用基于晶振特征的重点雷达信号快速靶向识别，与常规的方法相比，该方法针对性更强，所需参数更少，算法简单，易于实现。为对比算法的识别效果，分别利用PRI搜索法和改进PRI变换法对脉冲流进行处理。

3.1 算法优越性

同一部多功能雷达有很多种工作模式，因工作任务不同，该雷达的工作模式随着工作任务进行切换，每种工作模式下，各种工作参数也不相同。表1和表2是对两部多功能雷达的参数设置。为方便讨论，将多功能雷达的工作模式简化，每个工作模式完整执行一个周期，就执行下一个工作模式，如此循环执行。

表1 基于晶振特征的雷达基本参数设置

表2 多功能雷达的工作参数设置

PRI搜索法采用文献[6]中的算法，PRI搜索范围为600～2100 μs，图5为PRI分选算法的分选结果，从中分选出32个不同的PRI值，实际只有两部雷达信号，分选出来的PRI值是搜索范围内的一部雷达信号的一个PRI值或者连续几个PRI值的叠加；图6是改进的PRI变换算法对脉冲流的处理结果，采用文献[7]中的算法，对算法中的参数设置如下：α=0.38,β=0.25,γ=3,τmin=600,τmax=21 400,K=5000,ξ0=0.03，该算法对于参差、组变或者抖动的雷达信号无能为力，当要识别的雷达信号中含有PRI抖动的雷达信号，没有固定的自重复周期，该算法对于这种复杂的雷达信号基本失去作用。经过分析，对于PRI变化复杂，且包含一定量的PRI抖动信号的情况，传统的PRI分选算法无法准确地对该雷达信号进行分选。

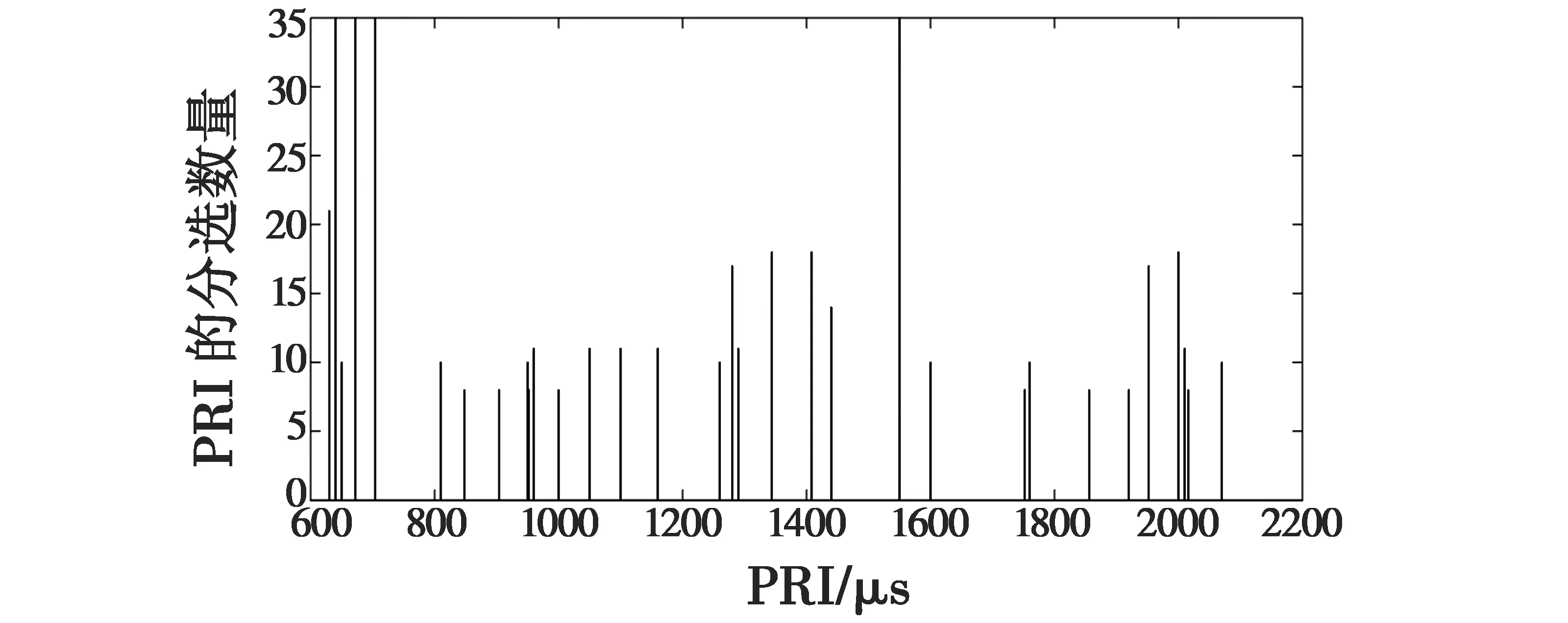
图5 PRI分选算法的分选结果Fig.5 Sorting results of PRI sorting algorithm

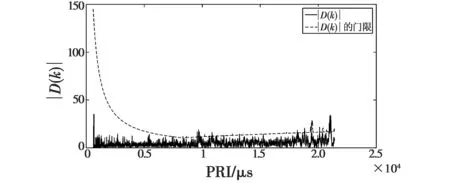
图6 改进的PRI变换法的分选结果Fig.6 Results of the improved PRI transformation

图7为全脉冲的识别，从中可以看出，当脉冲流中的脉冲为理想值时，基于晶振特征的重点雷达信号快速靶向识别算法对复杂的PRI雷达信号可以准确地识别。图8为利用载频对脉冲流进行一个预分选，再利用重点雷达信号的相对脉冲基本间隔对重点雷达信号的脉冲进行识别。

图7 全脉冲的识别Fig.7 Recognition of overall pulses

图8 工作模式的识别Fig.8 Identification of working modes

根据以上分析可知，基于晶振特征的重点雷达信号快速靶向识别算法可以对PRI参差、组变、抖动等脉冲进行准确分选识别，这是常规PRI分选算法难以克服的困难。尤其对PRI在一个较大范围内抖动的雷达信号，本身的PRI变化规律难以寻找，只有从PRI的产生原理着手，才能对该系列的脉冲进行识别。该算法可以准确识别出同一部多功能雷达的所有工作模式的脉冲，且可以做到分别对不同的工作模式进行识别，这是常规的分选算法难以做到的。

3.2 适用情况

以上得到的结果是理想情况下各种算法的处理情况。由前文分析可知，随机误差是纳秒量级，为模拟实际接收到脉冲流的情况，本文对理想的脉冲流中的脉冲到达时间添加随机误差，随机误差服从均值为零的正态分布，且标准差设置为σ。在不同的频率容差条件下，基于晶振特征的重点雷达信号快速识别算法的适用情况如表3所示。

表3 改变频率容差情况下的1000次Monte Carlo实验

表3中ushe取值为4，取值过小，很容易将其他雷达脉冲也判断为要识别的雷达脉冲信号，取ushe大于4来降低其他雷达脉冲的影响，提高识别正确率。在相对晶振基本间隔取值一定的条件下，为使对雷达脉冲的识别正确率满足一定的条件，门限tclkshe值的设置是由标准差σ决定的。

表3中对不同随机误差取值，改变相对晶振基本间隔值进行多次仿真，得出每个相对晶振基本间隔值对重点雷达信号的识别正确率，利用识别正确率判断该相对晶振基本间隔对重点雷达信号的识别的可靠性。若脉冲的识别正确率小于10%，则认为此时的相对晶振基本间隔偏离理想值较大，不能完成对重点雷达信号的识别；若重点雷达的脉冲的识别正确率在85%以上，则认为这个误差范围内，都能对重点雷达信号的脉冲进行很好的识别。如果有两部雷达的相对晶振振荡频率都在这个区间范围内，则认为该方法无法对两部雷达中的某部雷达信号进行准确的识别。

如表3所示，进行了3个标准差值的仿真，有2个值是为了对实际情况进行拓展。脉冲流中脉冲到达时间的实际值偏离理想值的随机误差取值是在纳秒量级，在理想值上添加标准差σ为0.003 9 μs，基本符合实际情况。例如对晶振的振荡频率是1.25 MHz，相对晶振基本间隔是8 μs进行分析，频率容差在1.25 Hz之内对该雷达信号的识别效果都很好，频率容差在1.25～12.5 Hz对该雷达信号的识别效果较差，当频率容差大于12.5 Hz就无法对该雷达信号进行识别。因此，基于晶振特征的算法对该雷达的晶振频率的容差分辨率的分布范围是在1.25～12.5 Hz。同理，对于晶振频率为10 MHz的雷达，该算法的频率容差分辨率的分布范围在10～100 Hz。

综上所述，对于不同雷达的晶振特征，基于晶振特征的算法对晶振容差的分辨率最小值在几赫兹到上百赫兹之间，符合实际需求。

在一定仿真分析的基础上改变随机误差，保证其他参数不变的情况下，进一步验证随机误差对识别正确率的影响，具体的识别正确率如表4所示。

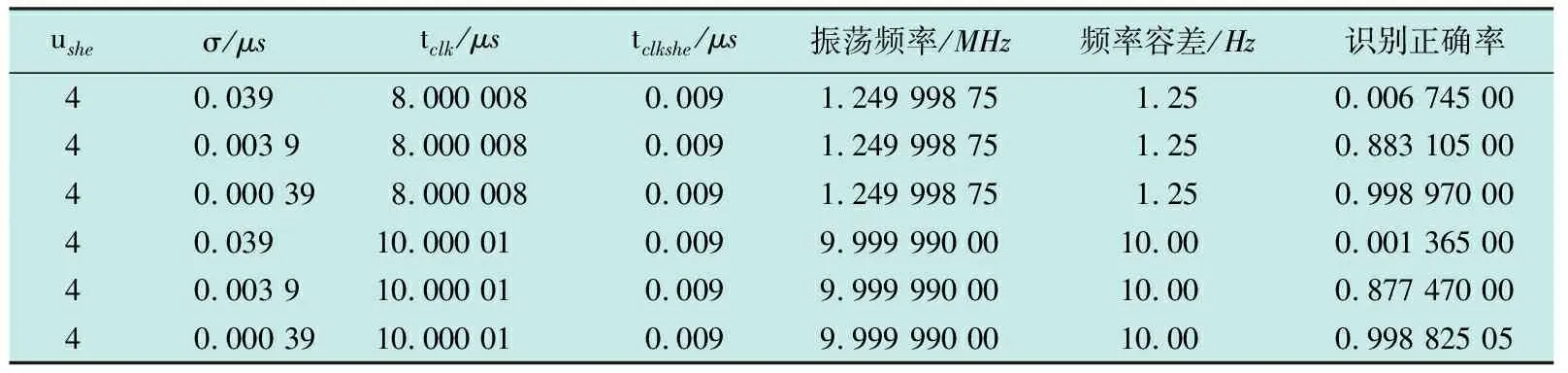
表4 改变随机误差情况下的1000次Monte Carlo实验

可以看出，当其他参数设置合理，识别正确率能满足实际需求。当随机误差增大时，不改变其他参数的设置，识别情况难以满足需求。当随机误差减小时，识别正确率较高。

3.3 基于晶振特征识别的快速性

如表5所示，对比了几种算法处理同一脉冲流所需要的时间，明显可以看出,基于晶振特征的重点雷达信号快速靶向识别算法所消耗的时间更少，且完成了对重点雷达信号的识别。PRI搜索法和改进PRI变化法只完成了对脉冲的分选。

表5 1000次Monte Carlo实验的时间统计

4 结束语

本文提出利用重点雷达信号的晶振特征对脉冲流进行识别处理，该算法从PRI的生成原理着手考虑，PRI的变化复杂与否对该算法的识别情况影响很小，相对于传统算法，PRI变化越复杂，该算法的优越性越强，通过与PRI搜索法与改进PRI变化法进行对比，验证了该算法对复杂雷达信号的处理速度和识别效果都是优于传统方法的,通过增加随机误差亦验证了该算法在实际环境下的可行性。传统的PRI处理方法可以实现信号的盲源分离，但实时性和针对性较差。基于前期的雷达对抗情报侦察，能够对给我方产生威胁的雷达信号有一定的了解，能得到想要的雷达晶振特征，满足该算法对脉冲流处理前需要重点雷达信号的晶振特征这个条件。在紧急情况下，需要对重点雷达信号进行快速识别，因此本文具有一定的实际应用价值。