遗传-和声搜索算法下的MIMO雷达正交多相码设计
谢雷振, 陈怡君, 康 乐, 张 群, 梁贤姣
(1.空军工程大学信息与导航学院,西安 710077; 2.中国人民解放军95100部队,广州 510405)
0 引言
多输入多输出雷达是一种新兴的有源探测性雷达,其在低慢目标检测、反隐身等方面具有极大优势[1]。它继承了相控阵雷达优点的同时,因为其波形的正交性而能够在整个空域中进行全方位探测,所以研究MIMO雷达在理论上和实际中都有重要的价值[2-3]。
发射波形的优劣是影响MIMO雷达目标识别等性能的关键因素。MIMO雷达从产生至今,正交波形设计都是其中一个重要的研究方向[4-5]。主要通过构造合适的代价函数,使用适合的优化算法来得到全局最优的信号波形[1-10]。在构造代价函数方面,文献[6]利用信息论的方法,通过回波的互信息以及最小均方误差准则对波形进行优化;文献[7]提出零相关区域的概念,它关心该区域内的旁瓣,忽略区域外的旁瓣,使得邻近距离单元回波间的干扰得到有效的消除。在优化算法方面,文献[8]提出利用模拟退火算法设计正交多相码信号,得到了比较低的自相关旁瓣;文献[9]用遗传算法来设计正交多相编码和正交离散频率编码波形,降低了发射信号的自相关旁瓣峰(Autocorrelation Sidelobe Peak,ASP)和互相关峰(Cross-correlation Peak,CP);文献[10]用遗传禁忌混合算法进行优化,使得自相关旁瓣峰值和互相关峰值进一步降低。由于上述波形设计方法直接应用相应的启发式算法,没有考虑代价函数在全局最优解附近变化不大的特点,存在自相关旁瓣峰值和互相关峰值比较高[9],并且收敛速度慢的问题[10]。
本文提出了一种新的MIMO雷达正交多相码设计方法,它基于和声搜索算法和遗传算法,将和声搜索算法的邻域搜索思想加入到遗传算法之中,能够在提高收敛速度的条件下有效降低正交波形的自相关旁瓣峰值和互相关峰值。
1 MIMO雷达正交多相码设计准则
假设这样一个雷达系统,它有L个发射信号,每个信号的长度为N,那么可以将发射信号表示为
sl(t)=ejφl(n)n=1,2,…,N,l=1,2,…,L
(1)
式中:l表示第l个信号;n表示第n个相位[9-10]。如果多相码有M个可选离散相位,那么相位可以选择的值表示为
(2)
所以对于一个码长为N、信号为l的多相码集S,用L×N的相位矩阵表示为[9-10]
(3)
根据信号的相关属性,可以得到
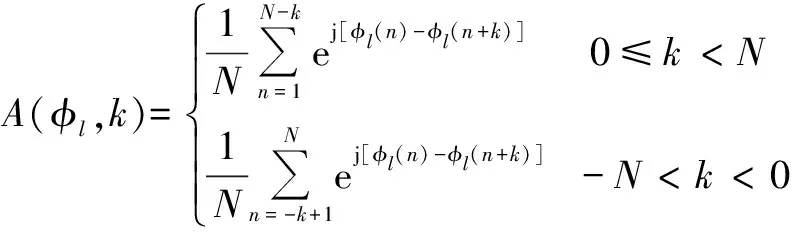
(4)
及
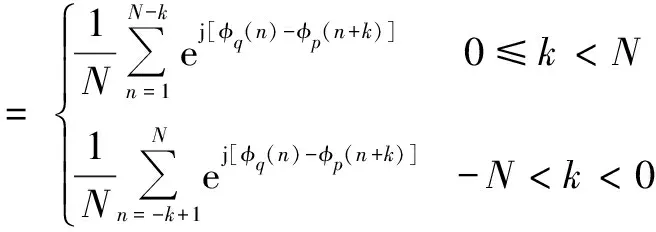
(5)
式中:p≠q并且l,p,q=1,2,…,L;A(φl,k)是信号的非周期自相关函数;C(φp,φq,k)是任意两个信号的非周期互相关函数[9-10]。
为了得到尽可能优良的正交信号,所得信号应满足
(6)
及
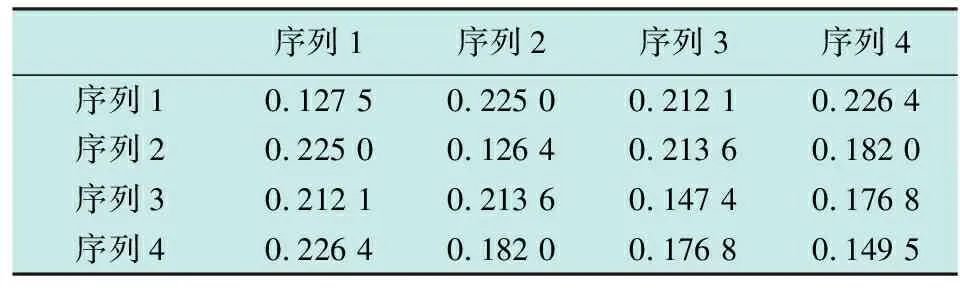
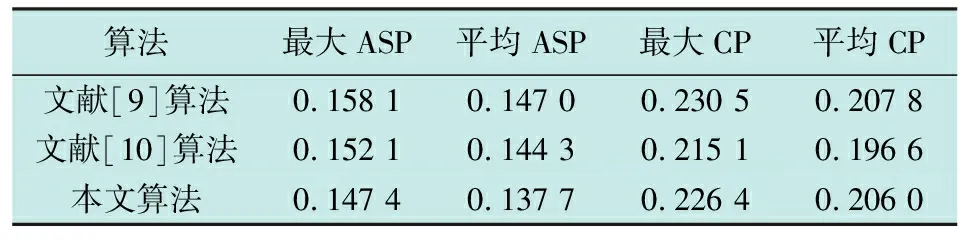
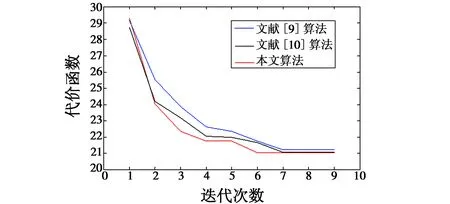
C(φp,φq,k)=0 -N (7) 然而,由能量守恒定律可知,设计的波形只能近似满足上式。 在MIMO雷达正交多相码的设计中,多个方面的因素都会对最后的结果有所影响,这些因素包括自相关旁瓣峰值能量、互相关峰值能量、总的自相关旁瓣能量以及互相关能量,综合这些因素可以使得到的信号性能更加稳定。所以,代价函数可以选取为以上因素的总和,表示如下[9-10] (8) 式中:w=[w1,w2,w3,w4]为代价函数的加权系数;L为发射信号个数;M为可选离散相位个数。 MIMO雷达正交多相码优化可以转化为最小化相应代价函数[9] minE(x)x=φl(n),n=1,2,…,N,l=1,2,…,L (9) 式中:E为式中的代价函数;φl(n)(0≤φl(n)<2π)为第l个信号中第n个脉冲的相位。 遗传算法是一种模拟自然界中生物自然演化规律的算法[11],通过设定初始的种群,然后以迭代的方式对种群进行选择、交叉、变异操作,最终得到适应性更强的种群[12]。和声搜索算法是一种模拟乐队中乐师反复演奏音乐直到音律达到一个和谐状态的算法,它通过设定初始的和声库,然后对和声库邻近的可能解反复进行搜索,最终得到问题的最优解[13]。 本文通过将遗传算法与和声搜索算法结合来解决式(9)这一最优化问题。将和声搜索算法应用到遗传算法之中,先进行遗传算法,这样可以得到优化到一定程度的序列,在得到的序列基础上再使用和声算法。 假设遗传算法种群大小为C、搜索总次数为Y、和声搜索算法搜索总次数为Z。每次搜索的代价函数结果可以表示为 E(x)yzy=1,2,…,Y,z=1,2,…,Z (10) 式中,x为正交多相码序列φl(n)。设n和m分别为遗传算法与和声搜索算法的搜索次数,则相应的种群可以表示为T(n,m),种群的每个个体可以表示为xi(i=1,2,3,…,C)。 混合算法的主要步骤如下。 1) 编码。采用二进制编码方式。设定单一个体的序列个数为n,其中每一个序列都用二进制编码表示,序列分别为li(i=1,2,…,n)位,那么这个个体x可以表示为 (11) 该编码串的总长度表示为 (12) 如果参数编码采用二进制编码,则四相码的4个相位分别为{0 π/2 π 3π/2},对应的编码为{00 01 10 11}。 2) 初始化。随机产生一个初始的种群T(0,0),令加权系数为w=[w1,w2,w3,w4]=[1,1,1,1]。确定遗传算法的参数,包括遗传代数G,种群大小C,交叉概率pc,变异概率pm等[9]。确定和声搜索算法的参数,包括和声记忆库的大小Hs(Harmony Memory Size, HMS),记忆库取值概率Hr(Harmony Memory Considering Rate,HMCR),音调微调概率Ph(Pitch Adjusting Rate, PAR)以及最大搜索次数Gh[12]。 3) 适应度计算。适应度越强的越容易选择到下一代,适应度可以用代价函数的倒数来表示 F(x)=1/E(x)x∈T(n,m) (13) 式中:T(n,m)为遗传算法搜索n次,和声搜索算法搜索m次后的种群;F越大表示个体的适应度越强[11]。 ① 根据适应度值的大小对种群中各个个体进行排列[11],得到每个个体排列好的种群T*(n,m),并计算新的适应度为 (14) ② 计算出每个个体的累积概率为 (15) ③ 生成(0,1)之间的随机数rs。 ④ 若rs ⑤ 重复③,④共C次。 5) 交叉操作。对群体中所有个体进行两两配对,并且根据交叉概率pc判断是否需要进行交叉,交叉采用单点交叉。单点交叉操作如下: ① 从种群中每次随机取出不同的配对好的个体x1和x2,并设定掩码c(0或者1)。 ③ 将x1和x2中第rm位上的值与c进行异或操作,并用所得值代替x1和x2中的值[11]。 6) 停止准则判断。判断搜索次数是否达到优化的要求。如果满足,继续进行下一步;否则返回3)。 7) 变异操作。本文将遗传算法中的变异算子替换为和声搜索算法,具体操作如下。 ① 对种群中的所有个体,首先生成(0,1)之间的随机值r,如果r≤pm,则进行和声搜索算法的操作;否则继续对下一个个体进行①操作。 ② 和声搜索算法的初始化。将当前种群中的所有个体作为和声搜索算法的初始解。对和声搜索算法的各项参数进行初始化,包括和声记忆库的取值概率Hr,音调的微调概率Ph。 ③ 判断和声搜索算法的次数是否达到要求。如果满足,结束7);否则继续以下步骤。 (16) 否则继续进行和声搜索算法。 ⑥ 转至③。 8) 判断遗传算法的搜索次数是否达到要求。如果满足,停止算法,输出结果;否则,返回3),采用新的种群继续进行遗传算法的搜索。 图1为遗传-和声搜索算法的流程图。 图1 混合算法的流程图Fig.1 Flow chart of the hybrid algorithm 仿真基本参数设置为:码长N=40,发射信号个数L=4,可选离散相位个数M=4,即发射4个长度为40的四相码脉冲序列,相位为{0 π/2 π 3π/2},表示为{1 2 3 4}[10]。遗传算法部分的初始参数设置:交叉概率pc为0.95,变异概率pm为0.1。和声搜索算法部分的初始参数:和声记忆库概率Hr为0.99,音调微调概率Ph为0.1。遗传算法的种群大小与和声搜索算法的和声库大小保持一致,为40。通过迭代的方法更新种群与和声库,最小化式(8),产生一组满足式(6)和式(7)的多相码序列,然后分别求出序列的自相关和互相关。表1为优化后的正交多相码序列。表2为所得序列的相关特征,其中主对角线是归一化的ASP,表中其他部分是归一化的CP。图2为各脉冲序列自相关曲线。图3为各脉冲序列之间的互相关曲线。 表1 优化得到的相位序列(N=40,L=4,M=4) 表2 正交多相码的ASP和CP(N=40,L=4,M=4) 图2 各序列的自相关曲线Fig.2 Autocorrelation curves of each sequence 表3为本文算法和其他算法的结果比较,容易看出,本文算法得到的序列平均ASP为0.137 7,平均CP为0.206 0,相对于文献[9]中的算法都有所下降,并且通过图2和图3能够看到,所得序列的能量分布比较均匀。与同样在遗传算法基础上改进的文献[10]相比,本文算法ASP明显降低,同时CP也表现出了良好的效果。图4为不同算法的收敛曲线,容易看出,本文方法的收敛速度高于文献[9-10]中的方法。 图3 各序列的互相关曲线Fig.3 Cross-correlation curves of each sequence 算法最大ASP平均ASP最大CP平均CP文献[9]算法0.158 10.147 00.230 50.207 8文献[10]算法0.152 10.144 30.215 10.196 6本文算法0.147 40.137 70.226 40.206 0 图4 不同算法的迭代曲线Fig.4 Iterative curves of different algorithms 通过仿真结果可知,本文算法的结果优于文献[9]中仅使用遗传算法的优化结果,同时在保持互相关性较好的前提下,又在自相关性方面优于文献[10]中提出的算法,收敛速度也有所提高。本文算法由于结合了两种算法的优点,因而具有很快的收敛速度,同样的迭代次数,所得结果优于文献[9-10]中的算法。仿真结果验证了所提算法的优势。 本文提出的基于遗传-和声搜索算法的MIMO雷达正交多相码设计方法,通过将两种算法相结合,使得遗传算法的全局寻优能力及和声搜索算法优良的邻域寻优能力得到共同发挥,因此得到了更强的优化能力。同时,采用了最优保存策略,使得每次迭代得到的最优解不易被破坏,从而进一步加快了向最优解靠拢的速度。相比于已有的方法,在得到良好互相关峰值的同时,降低了自相关旁瓣,加快了收敛速度,更适合MIMO雷达目标探测使用,增强其目标检测能力。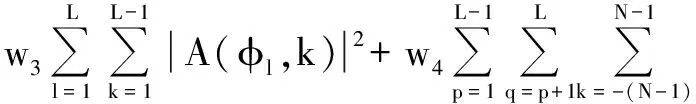
2 遗传-和声搜索算法的步骤


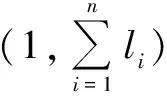

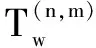

3 实验结果及分析




4 结论

