一种改进的锂电池SOC粒子滤波估计方法①
王 露,王顺利,陈 蕾,张 丽,刘小菡
(西南科技大学、信息工程学院自动化系,四川 绵阳 621010)
引言[1]
锂电池荷电状态(state of charge,SOC)的变化为非线性,其受各种因素如电化学反应、温度等影响,无法直接测得,这使得对其准确估算成了一个难题。人们针对非线性估计问题在卡尔曼滤波基础上提出扩展卡尔曼(EKF)、无迹卡尔曼(UKF)等改进算法。EKF用一阶泰勒展开处理非线性问题,UKF不需线性化,利用采样点的概率分布近似状态向量的概率密度函数,但都局限于高斯分布。PF不需定系统和观测噪声为高斯分布,可应用于非线性非高斯模型,优于前述方法。高建树等人[2]在SIR-PF算法上提出了改进估算SOC的PF算法,为电动汽车电池SOC的估算找寻新思路;乌兰花等人[8]在PF权值更新中加入神经网络估计锂电池SOC,取得了更好性能;Xiong R[6]等人采用一种双尺度PF法对不同时间尺度下的系统状态和参数进行了估计预测,有很好稳定性。本文在搭建合适的锂电池等效电路模型基础上,建立基于安时积分和PF修正的SOC估计改进方法,实现算法模拟仿真评估,通过磷酸铁锂电池放电测试数据对算法进行验证。
1 锂电池等效电路模型建立
实现滤波算法的前提工作是选择搭建合适的锂电池等效电路模型。对于不同的研究与应用要求,需要选取不同精度和复杂度的模型。在权衡准确性和复杂度之后,本次实验选用结合RC模型和Thevenin模型的二阶RC模型。如图1所示,其中U oc为电池的开路电压,在特定温度下与SOC呈一定的函数关系。R0为欧姆内阻,R1、R2为极化内阻,C1、C2为极化电容,R1C1电路时间常数τ1模拟电池电流突变,R2C2的τ2模拟电压缓变。
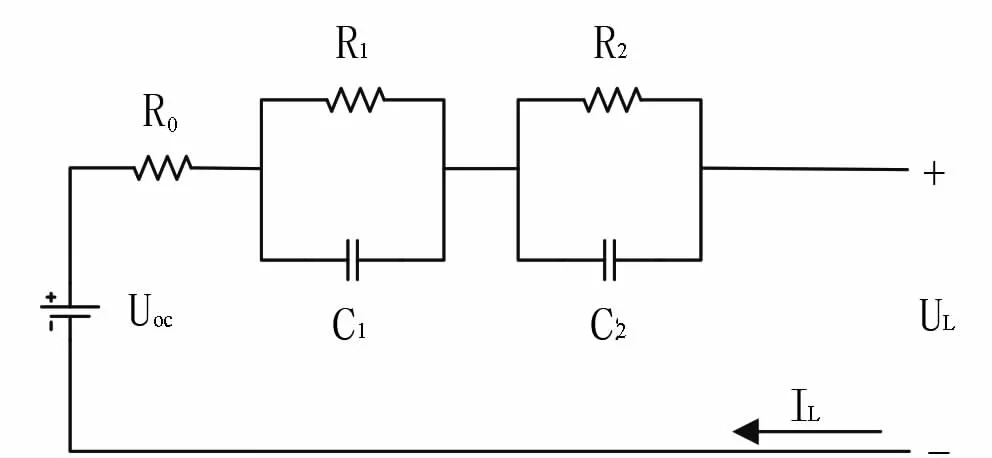
图1 锂电池等效电路模型Fig.1 Equivalent circuit model of the lithium battery
工作电流I L为系统输入,图中表示放电。电池端电压U L为观测值,得出离散化后的状态空间模型如下。


式(1)为状态方程,T S为采样间隔,ωk表示系统的过程噪声;式(2)为量测方程,νk表示系统观测噪声。U OC(SOC(k))关系曲线可以由开路电压与SOC的标定实验得到。二阶RC模型的其他参数(欧姆内阻R0、电化学极化内阻R1与电容C1、浓差极化内阻R2与电容C2)使用HPPC测试实验进行辨识,利用最小二乘法拟合电压曲线得到相应的参数。
2 基于PF的SOC估算
PF是一种用蒙特卡罗(SMC)方法和递推贝叶斯滤波算法估计的统计滤波方法,它将贝叶斯估计的积分运算通过SMC处理成求和运算,得到系统状态的最小均方差估计。其基本思想是采集随机样本,根据量测不断调整粒子的权重和位置以修正之前的经验条件分布。与其它滤波方法如KF、EKF和UKF等相比,PF不必对系统状态作任何先验假设,理论上可适用于任何能用状态空间模型描述的随机系统。根据前面建立的等效二阶RC模型所得到的过程与量测方程,应用PF对SOC的估算,可以提高SOC估算的精度,在保证同样精度的情况下,可减少算法的粒子采样数,从而减少计算量。
程序流程图如图2,其过程可用以下步骤描述:
(1)初始化:利用先验概率p(x0)产生N个SOC初始粒子粒子权值
(2)算法循环过程:①更新。根据系统更新方程,得到下一时刻先验概率样本更新粒子权重
应计盈余管理。虚拟变量。采用修正琼斯模型 (Dechow等,1995[26]) 计算操控性应计,应计盈余管理的计算模型如下,先将模型 (1)分年度分行业回归,再将估计出来的回归系数带入模型 (2)。

图2 粒子滤波流程图Fig.2 Flow diagram of PF algorithm
⑥判断程序结束条件,若未结束,时刻k=k+1,到①步。
3 实验与分析
电池测试实验采用LFP电池进行测试,充电上限电压3.65V,放电下限2.0V,额定容量10Ah。首先需要对选取的二阶RC模型模型进行参数辨识。实验内容为[2]:
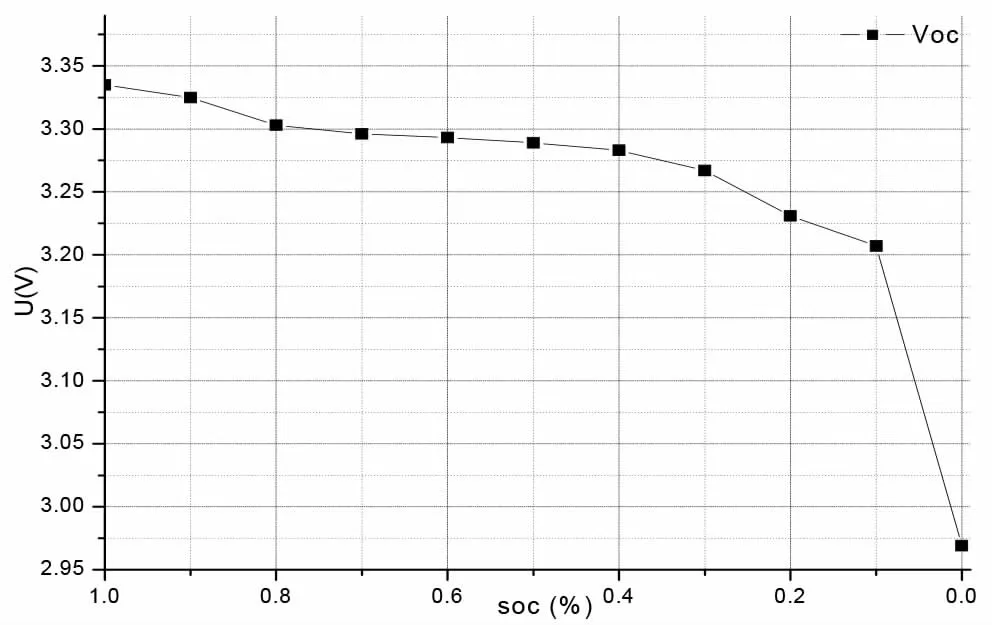
图3 OCV-SOC标定曲线Fig.3 OCV-SOC calibration curve
(1)开路电压(OCV)辨识:在室温(25℃)下,充满电静置1小时,放电每放出10%SOC时静置30min,此时电压作为OCV,对数据整理得到OCVSOC关系曲线如图3。拟合曲线得关系式(4)。
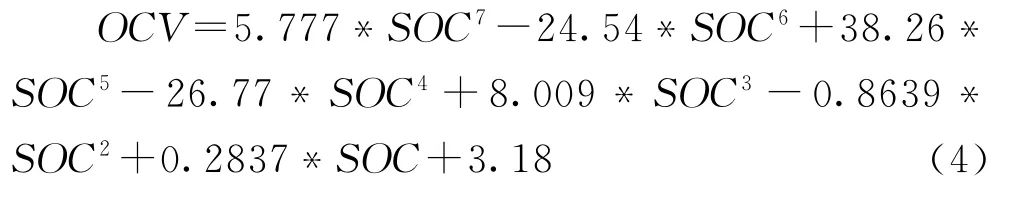
(2)其他参数(R0、R1、C1、R2、C2)辨识:测试曲线如图4,R0等于由放电开始和结束瞬间电压降平均值与电流之比。
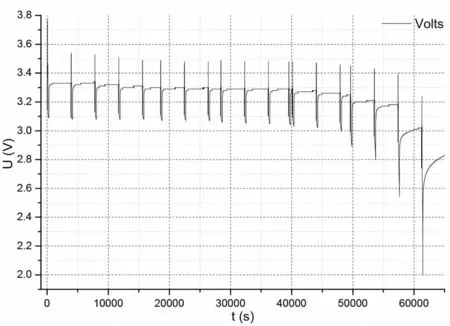
图4 HPPC测试曲线Fig.4 HPPC testing curve
脉冲放电后的静置时间,RC为零输入响应,端电压方程如式(5),
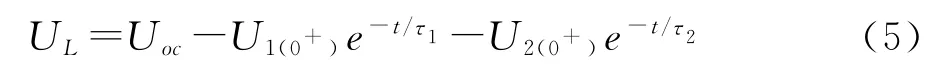
U1(0+)为放电结束瞬间R1C1电路电压初始值,U2(0+)为放电的初始值,τ=RC,利用最小二乘法拟合脉冲放电结束后的电压曲线可得到τ1和τ2。脉冲放电过程中,RC电路为零状态响应,端电压方程如式(6)。
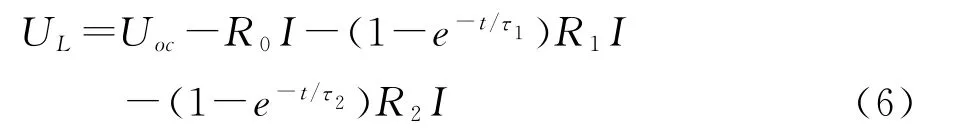
同样使用最小二乘法得到R1和R2,C1和R2可由τ/R得到。最后可以的到各参数与SOC的关系曲线方程。
(3)SOC估算仿真实验。使用实验得出的参数,有(1)~(3)式得到PF算法的过程递推方程和量测噪声方程,根据算法流程,模拟实际放电过程中电流变化的情况,进行SOC估算,得到仿真曲线图像,如图5。
模拟仿真结果表明,PF算法跟踪SOC有良好的滤波效果,其误差最终稳定在4%内,如图6。

图5 PF估算SOC跟踪曲线Fig.5 PF estimation tracking curve of SOC

图6 PF的跟踪误差Fig.6 Error of PF tracking
使用LFP电池实测数据对算法进行训练,对比仿真与实测数据跟踪效果,算法具有良好的稳定性。
4 结论
本文选择二阶RC等效电路作为LFP电池的等效模型,进行HPPC实验获取模型参数,得到算法所需的过程和量测方程。PF算法应用自适应重采样方法,提高了粒子有效性,同时减小算法的复杂度。结果SOC估计逐渐接近真实值,误差最终稳定在4%以下。使用实测放电数据训练算法,在保证精度的前提下,可以减少采样粒子数,减少计算量。下一步目标是算法精度的改进和锂电池实际工况中估算SOC的自适应PF算法应用。

