三相四线制软开关SiC逆变器软开关工况分析

朱应峰，何 宁，胡长生，徐德鸿

（浙江大学电气工程学院，杭州 310027）

三相四线制逆变器广泛应用于不间断供电电源，未来将广泛应用于微网和分布式新能源发电系统。三相四线制逆变器开关频率上限主要受到功率器件动态损耗的限制，导致较大的输出滤波元件的体积，最终限制了逆变器的小型化。

软开关技术已广泛应用于三相逆变器。文献[1]提出了直流侧谐振RDCL（resonant DC link）逆变器；文献[2]提出了辅助谐振变换级ARCP（auxiliary resonant commutated pole）；文献[3]提出了耦合电感零电压转换逆变器；文献[4]提出了准谐振直流环节三相四线制逆变器；文献[5]提出了辅助谐振换向极三相四线制逆变器。针对本文研究的直流侧谐振逆变器，文献[6～7]提出了适用于三相三线制逆变器的零电压开关空间矢量调制ZVS SVM（zero-voltage-switching space vector modulation）方法。基于ZVS SVM方法原理，文献[8]提出了适用于三相四线制逆变器的零电压开关正弦脉宽调制ZVS-SPWM（zero-voltage-switching sinusoidal pulse width modulation）方法，该电路只需引入1个辅助开关和2个较小的无源元件，就可以实现电路中所有开关器件的零电压开关。基于ZVS-SPWM方法，软开关辅助电路只有当负荷电流从逆变桥臂的反并联二极管到同一桥臂对偶的主开关换流时，才动作一次，其他时刻该逆变器的工作类似PWM逆变器。

宽禁带器件SiC MOSFET的输出电容呈现非线性，其容值会随所承受的电压变化。文献[9]指出，SiC MOSFET的输出电容Coss与管压的均方根成反比。以SiC MOSFET器件C2M0025120D为例，电压较低时输出电容可达几nF，电压较高时只有数百pF。由于零电压开关的实现条件与谐振电容有关，谐振电容包含开关器件的输出电容和外并联电容，而在谐振过程中SiC MOSFET的端电压在0和最高值之间变化，这样谐振电容容值也随着管压变化，造成理论分析变差。因此针对SiC MOSFET的输出电容非线性的特点，改进零电压开关条件的分析和参数设计方法是有必要的。

本文首先简单介绍了阻性负载下三相四线制零电压开关逆变器ZVS SPWM方法，分析了SiC MOSFET的输出电容非线性对零电压开关条件和器件应力的影响，提出了开关器件等效输出电容值的提取方法，修正了零电压开关条件和器件应力的计算值。最后在一台应用SiC MOSFET器件的10 kW三相四线制零电压开关逆变器平台上进行了实验验证。

1 ZVS SPWM方法简介

图1所示为三相四线制零电压开关逆变器拓扑。相比传统硬开关拓扑，直流母线串联了一个辅助支路，该辅助支路包含辅助开关S7、箝位电容Cc和谐振电感Lr。在三相桥臂的主开关反并联二极管向主开关换流之前，关断辅助开关S7，谐振电感与电路中的谐振电容（Cr1～Cr7）发生谐振，将三相桥臂两端的电压Vbus谐振到0，为主开关创造零电压开通的条件。

以三相平衡阻性负载为例分析换流过程，三相负载电压（ua,ub,uc）和三相滤波电感电流（ia,ib,ic）如图2所示。根据三相电感电流的极性，可以把整个工频周期分成6个区域。后文均以区域1为例进行分析，在该区域中A相滤波电感电流为正，而B相和C相滤波电感电流为负。这里忽略LC滤波器引起的电流相移，假定负荷电流近似等于电感电流。

图1 三相四线制零电压开关逆变器拓扑Fig.1 Topology of three-phase four-wire ZVS inverter

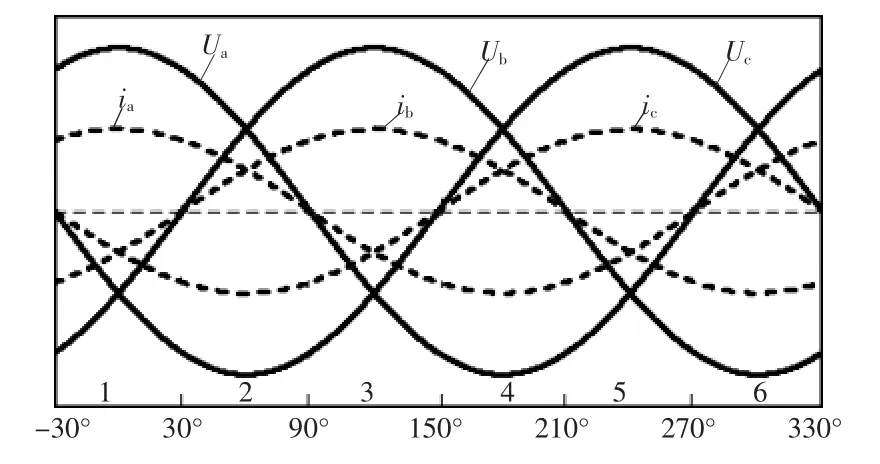
图2 三相负载电压和电感电流示意Fig.2 Schematic of three-phase load voltages and inductive currents

图3所示为传统硬开关三相四线制逆变器采用的SPWM方法，其中Uma、Umb和Umc分别为ABC三相的调制波，Vgs_s1、Vgs_s3和 Vgs_s5分别为主开关 S1、S3和S5的驱动电压。以C相换流过程为例，图4和图5分别为C相上桥臂导通和C相下桥臂导通的等效电路。由图可知，当C相由上桥臂导通切换至下桥臂导通时，存在1次从反并联二极管D5向主开关S2的换流。在一个开关周期内共存在3次不同时刻的反并联二极管向主开关换流，因此辅助支路需要工作3次以实现所有开关的零电压开通。为了减少辅助支路工作次数，降低调制的复杂度，将图3中3次反并联二极管向主开关换流的时刻平移到同一时刻，并保持各相占空比不变，如图6所示，应用此改进调制方法，辅助支路只需要工作1次就可以实现所有主开关的零电压开通。

图3 传统SPWM方法Fig.3 Traditional SPWM method

图4 C相上桥臂导通等效电路Fig.4 Equivalent circuit with D5conducting

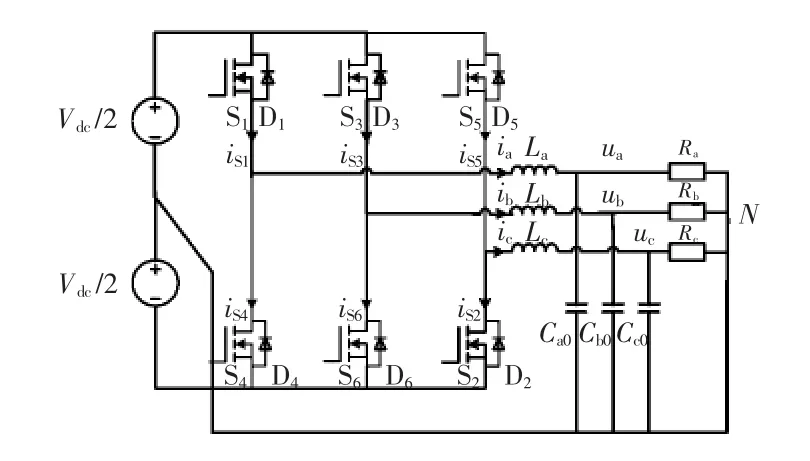
图5 C相下桥臂导通等效电路Fig.5 Equivalent circuit with S2conducting

图6 ZVS SPWM方法推演Fig.6 Derivation of ZVS-SPWM method

2 电路工作阶段分析

图7 开关周期的主要波形Fig.7 Main waveforms in switching periods

图8 阶段 2（t1～t2）等效电路Fig.8 Equivalent circuit on stage 2（t1～t2）

三相四线制零电压开关逆变器一个开关周期内电路各关键元件的波形如图7所示。简单介绍主开关和辅助开关零电压开通的原理。阶段1（t0～t1），三相主开关的反并联二极管D4、D3、D5导通；阶段2（t1～t2），t1时刻关断辅助开关 S7，开关管谐振电容Cr7、Cr1、Cr6、Cr2和谐振电感 Lr开始谐振, 主开关 S1、S6、S2两端的电压在t2时刻谐振到0，为主开关的零电压开通创造了条件，该阶段等效电路图如图8所示；阶段 3（t2～t3），t2时刻主开关S1、S6、S2的反并联二极管 D1、D6、D2续流，在该阶段内给主开关 S1、S6、S2加上开通信号，主开关零电压开通实现；阶段4（t3～t4）,t3时刻反并联二极管 D1、D6、D2续流结束后自然关断，二极管 D4、D3、D5开始向主开关 S1、S6、S2换流，t4时刻换流结束，此时谐振电感电流等于负载电流 ia；阶段 5（t4～t5），t4时刻开通主开关 S4、S3、S5进行直通，为谐振电感进行充磁，该阶段额外增加的谐振电感电流iadd对主开关的零电压开通起决定作用；阶段 6（t5～t6），t5时刻关断主管 S4、S3、S5，开关管谐振电容 Cr7、Cr4、Cr3、Cr5和谐振电感 Lr开始谐振，在t6时刻辅助开关S7两端的电压谐振到0，为辅助开关的零电压开通创造了条件，该阶段等效电路如图9所示。t6时刻辅助开关工作结束。

图9 阶段 6（t5～t6）等效电路Fig.9 Equivalent circuit on stage 6（t5～t6）

3 开关器件输出电容对零电压开关条件和电压应力的影响

3.1 零电压开关条件和电压应力理论值的误差与谐振电容误差关系

零电压开关实现所需阶段2的谐振时间Tr[14]为

式中：Lr为谐振电感；Cr为谐振电容，Cr=3（Coss1+Crex1）+Coss7，Coss1为主开关输出电容，Crex1为主开关外并联电容，Coss7为辅助开关输出电容。

零电压开关实现所需的最大谐振电感电流[14]iLrmax为

式中：Vdc为母线电压；Po为输出功率；Im为A相滤波电感电流幅值；θ为A相电压相位。

电路工作中开关器件电压应力[14]vdsmax为

式中，Ts为开关周期。

谐振电容存在误差△Cr，会导致谐振时间误差△Tr，即

谐振电容存在误差△Cr，会导致最大谐振电感电流误差 △iLrmax，即

谐振电容存在误差△Cr，会导致开关器件电压应力误差 △vdsmax，即

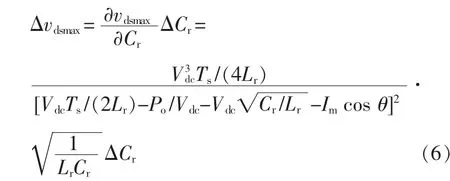
3.2 SiC MOSFET输出电容影响理论计算精度的原因

由第3.1节可知，理论计算中谐振电容误差△Cr会导致理论计算的零电压开关条件和电压应力存在误差。由于 Cr=3（Coss1+Crex1）+Coss7，外并联电容Crex1误差忽略不计，谐振电容误差为开关器件的输出电容误差。

图10（a）为主开关器件SCT2080KE寄生电容与管压的关系[10]，当管压从1 V上升至774 V时，输出电容Coss1从2 nF大幅减小到0.08 nF。图10（b）为辅助开关器件C2M0025120D寄生电容与管压的关系[11]，当管压从1 V上升至774 V时，输出电容Coss7从3.4 nF大幅减小到0.22 nF。本实验中，在阶段2和阶段6的谐振过程，主开关和辅助开关的管压均在0～774 V之间变化。而理论计算中，主开关和辅助开关输出电容均取值为管压774 V时的容值，导致理论计算中的输出电容误差较大，故谐振电容值存在较大误差△Cr，由此可知会导致理论计算的零电压开关条件和电压应力存在较大误差。

图10 开关器件寄生电容与管压关系Fig.10 Parasitic capacitance of switches vs.drainsource voltage

3.3 开关器件等效输出电容提取方法

SiC MOSFET器件的输出电容可以表示[13]为

式中：vds为开关器件端电压；K、Vb、Co为仅和器件本身有关的常数。

谐振过程中开关器件的输出电容电荷变化量可以表示为

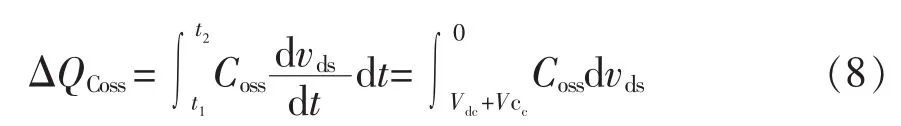
将式（7）代入式（8），可以解得

谐振过程中，开关器件端电压从Vdc+VCc变化到0。基于电荷守恒推导开关器件等效输出电容Coss_mod，表示为

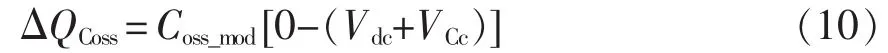
将式（9）代入式（10），整理可得开关器件等效输出电容为

结合图10可以分别拟合出主开关（SCT2080 KE）等效输出电容Coss1_mod中系数K=1 883 pF·V0.5、Vb=0.207 V、Co=21.43 pF 和辅助开关（C2M0025120 D）等效输出电容 Coss7_mod中系数 K=4 784 pF·V0.5、Vb=0.098 V、Co=-1.68 pF。结合式（11）可得开关器件等效输出电容与电压Vdc+VCc的关系，如图11所示。

图11 等效输出电容与电压关系Fig.11 Equivalent output capacitance vs.voltage

4 实验验证

本文搭建10 kW三相四线制零电压开关逆变器实验平台，平台设计参数为：fs=150 kHz，Vdc=700 V，ua=ub=uc=220 Vrms，Vbus=Vdc+VCc=774 V，La=Lb=Lc=0.66 μH，Ca0=Cb0=Cc0=2 μF，Po=10 kW，Im=21.4 A，Lr=4.9 μH，Coss7=0.22 nF，Crex1=Crex2=Crex3=Crex4=Crex5=Crex6=0.24 nF，Coss1=Coss2=Coss3=Coss4=Coss5=Coss6=0.08 nF，主开关器件型号为SCT2080KE，辅助开关器件型号为C2M0025120D。

图12和图13所示分别为0°相位处谐振电感电流和开关器件管压实验波形，实验中负载电阻Ra=Rb=Rc=14.9 Ω,故实际输出功率Po=9.73 kW、滤波电感电流峰值 Im=20.8 A，结合式（1）～式（3），可得0°相位处谐振时间、最大谐振电感电流和电压应力的理论值。

表1所示为实验与理论之间对比。由表1可见，谐振时间理论值与实验值误差为25%，最大谐振电感电流理论值与实验值误差为5.3%，电压应力理论值与实验值误差为2.6%，误差较大。

实验中VCc+Vdc=774 V，由图11可得主开关等效输出电容Coss1_mod为0.16 nF，辅助开关等效输出电容Coss7_mod为 0.34 nF，谐振电容修正值为 Cr_mod=3（Coss1_mod+Crex1）+Coss7_mod，用 Cr_mod替换式（1）～式（3）中的Cr，可得0°相位处利用等效输出电容修正后的谐振时间、最大谐振电感电流和电压应力的理论值，如表2所示。对比表1和表2可以看出，利用等效输出电容修正后的谐振时间理论值与实验值之间误差从25%减小到14%，最大谐振电感电流理论值与实验值之间误差从5.3%减小到2.7%，开关器件电压应力理论值与实验值之间误差从2.6%减小到2.3%。实验结果证明了利用等效输出电容求得的修正理论值与实验值之间误差较小，理论计算更为准确。

图12 0°相位的谐振电感电流波形Fig.12 Waveform of resonant inductive current at 0°

图13 0°相位的主开关和辅助开关管压波形Fig.13 Waveforms of main and auxiliary switches at 0°

表1 理论值与实验值之间对比Tab.1 Comparison between theoretical and experimental values

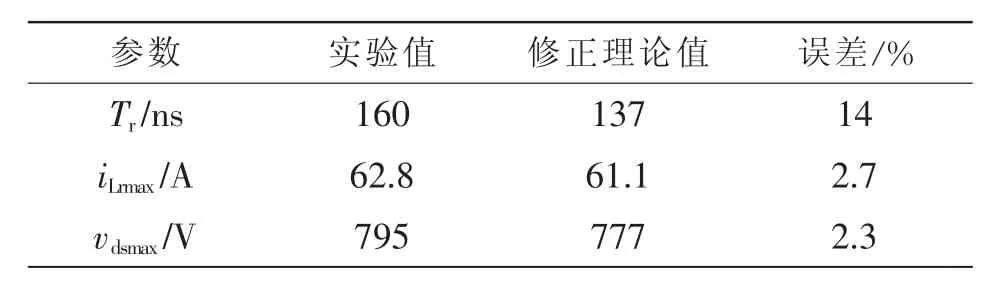
表2 修正理论值与实验值之间对比Tab.2 Comparison between modified theoretical and experimental values

5 结语

本文分析SiC MOSFET电容的非线性对零电压开关条件、电压应力、电路中电流的峰值等影响。利用开关器件等效输出电容的提取方法，修正了零电压开关条件的计算值，最后在一台10 kW SiC MOSFET器件的三相四线制零电压开关逆变器平台上进行了实验验证。