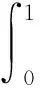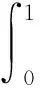分数次微分方程边值问题正解的存在性和唯一性
沈 英
(苏州幼儿师范高等专科学校,江苏苏州 215131)
随着分数次微积分理论研究取得了重大进展,分数阶微分方程在物理、化学、控制、工程等各个领域描述了许多不同现象,这些现象相比整数阶微分方程更能刻画事物内在的实质问题.目前对分数阶微分方程研究的方法比较多,其中不动点定理是较为常见且富有成效的工具,利用锥理论获得了丰富的成果.Bai Z[1]利用锥拉伸与压缩不动点定理,得到了分数阶微分方程两个正解的存在性.Liu Y[2]利用Avery-Peterson不动点定理获得至少3个正解的存在性.Liang S H[3]利用上下解结合不动点定理也获得了正解的存在性.但是,对于分数次微分方程边值问题正解唯一性的研究不多.为此,本文主要研究如下的分数阶多点边值问题:
(1)

1 预备知识

定义偏序:
x,y∈C[0,1],x≤y⟺x(t)≤y(t),t∈[0,1].
为了证明问题(1)正解的唯一性,我们使用的基本定理是偏序集上的不动点定理[4-6].
定理1 设(E,≤)是偏序集,在E中存在一个度量单位d,则(E,d)是一个完备的度量空间.假设E满足下列条件:如果{xn}在E中为一个单调非增数列,且xn→x,那么xn≤x,∀n∈N.
设T:E→E为一个单调非增的映射,且d(Tx,Ty)≤d(x,y)-Ψ(d(x,y)),x≥y.其中,Ψ:[0,+)→[0,+)是连续且单调非增的函数,Ψ在(0,+)上有定义且.
如果存在x0∈E使得x0≤T(x0),那么T有一个不动点.
考虑(E,≤)满足条件(H1):由于x和y是可以比较的,根据x,y∈E且存在z∈E.
定理2 假设定理1的条件和(H1)成立,则得到边值问题(1)正解的唯一性.
引理1 若0<β<2,h∈C[0,1],分数阶多点边值问题:
(2)
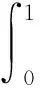
其中,
(3)
引理2 函数G(t,s)具有如下性质:
(a)G(t,s)是一个连续函数且G(t,s)≥0,∀(t,s)∈[0,1]×[0,1];
2 主要结论及其证明
定理3 边值问题(1)中的f如果满足下列条件:
(i)f(t,u(t))≠0,对任意的t∈Z⊂[0,1],这里μ(Z)>0(μ为测度),f:[0,1]×[0,+)→[0,+)是第二变量的单调非增的连续函数;
(ii)当u≥v,t∈[0,1]时,存在0<λ 则边值问题(1)存在唯一的正解. 下面将验证算子T满足定理1和定理2所有的假设条件. 首先,当u,v∈K且u≥v时,通过条件(i)可得: 这就证明了算子T是单调非减的. 另一方面,当u≥v时,通过条件(ii)可得: 由于函数h(x)=ln(x+1)是单调非减的,通过条件(ii)可知: =λln(‖u-v‖+1)·L ≤‖u-v‖-(‖u-v‖-ln(‖u-v‖+1)). 设ψ(x)=x-ln(x+1),显然ψ:[0,+)→[0,+)是连续单调非减函数,且有.此外,当u≥v时,则有: d(Tu,Tv)≤d(u,v)-ψ(d(u,v)). 由于G(t,s)≥0,f≥0,则得到: 由定理1可知,对于边值问题(1)至少有一个正解.如果(K,≤)满足条件(H1),那么由定理2可知该正解是唯一的.