面向车联网的交通信息传输博弈模型

樊 娜，朱依水，朱光源，唐 蕾，董 鸣，安宏海

(1.长安大学 信息工程学院，陕西 西安 710064；2.邯郸市交通运输局 基建处，河北 邯郸 056000)

0 引 言

由于车联网自身的网络拓扑结构多变、车辆节点连接短暂等特点以及车联网中节点自私性等问题，车联网环境中面向出行者的交通服务信息的安全可靠的传输面临了更多的挑战[1-4]。目前，研究人员针对车联网环境中信息传输的研究主要集中在两个方面：采用重复广播的思想以提高信息传输的效率[5-8]；改进路由协议提高信息传输效率。在车辆网环境中，常用的两类协议为按表驱动路由协议和按需驱动路由协议。研究人员多基于这两类协议进行改进，以期提高车联网中数据传输效率[9-11]。上述提出的这两类提高车联网信息传输效率的方法都是基于车联网中的车辆节点积极合作的假设前提，并未考虑现实车联网环境中节点的自私性因素的影响。在现实车联网环境中，存在可信度较高的节点出于自私目的而常常拒绝主动发布或转发交通服务信息的行为。由于此类自私节点的不合作行为，将对车辆网内部交通信息服务的有效传输产生消极作用，影响车辆网的整体效率。

本文基于博弈论原理，提出一种基于动态博弈论的模型，该模型能激励车联网内的节点采取合作行为，抑制自私节点和恶意节点的不合作行为，有效地优化车联网内部信息传输的环境。

1 问题分析

在现实车联网中，信息传输是交通流预测、协作驾驶等众多交通应用的关键环节。车联网本身是由装载传感设备的车辆节点和部署在道路两侧的各类路基设备构成。因此，结合在车联网的应用中，车联网中的信息传输通常包含两种方式：第一种方式为路基设备和车辆节点之间的信息传输。路基设备对在其有效通信范围内的车辆节点发布天气、路况等交通服务信息，节点收到信息后将转发该信息；此外车辆节点感知的交通信息也将发布给路基设备。第二种方式为车辆节点之间的信息传输。例如在城市交通中常见的应用场景：车辆节点作为“目击者”感知了道路堵车或车祸等其它道路突发事件，将主动向其有效通信范围内的车辆节点发布交通预警信息。在这两种方式中，如果节点能主动参与发布感知信息或者转发收到的消息，车联网内部的信息传输将进入良性循环。

然而车联网某些节点自身出于节省能量、独占道路资源等原因，常常会对于转发或主动发布等信息传输行为采取消极态度，从而导致车联网中类似的“搭便车”节点数量增长，直接影响车联网中信息传输的效率。

2 建立动态博弈论模型

2.1 模型基本原理

博弈论最初是经济领域提出的一种解决利益冲突的数学模型，经过多年的研究与发展，已经在生物工程学、计算机应用等多个领域获得了广泛应用。近年来,博弈理论被越来越多地应用在信息安全的众多领域。在本文的研究中，将采用博弈论的方法建立动态模型，以期激励车联网中的各个节点采取合作积极的行为，主动发布或者转发信息。博弃论中使参与者在特定约束条件下通过考虑其它参与者的对策做出相应的对策，以获得最大的收益，参与者之间存在利益或目标冲突，而利用博弈论来设计激励机制则能较好解决参与者之间的利用冲突问题。

通常，一个演化博弈论的标准设置如下：

(1)用户数量庞大，隶属于不同的种群，存在相互竞争的自私性关系；

(2)设置当前随机选择的节点数量为随机变量K,K≥0；

(3)假设每个种群有自身的策略集，种群中的用户从自身种群的策略集中选取策略,以获取最大化的收益。

基于上述设定，建立面向车联网的演化动态博弈模型，对该模型的基本要素描述如下：

参与者：车联网中所有车辆节点；

群体划分：通过分析，车联网中的车辆节点分为3个群体，正常节点为群体1，自私节点为群体2，恶意节点为群体3。每个群体中节点的数目是不确定的，随着时间的推移，某个节点有可能从原属群体转移到其它群体。假设车联网中车辆节点的分布服从泊松分布，在一次基于动态博弈模型的演化过程中，存在n个车辆节点参与博弈的概率可以通过式(1)计算

(1)

其中，参数θ>0,n≥1。

策略集：每个群体都有各自相对应的行为策略，在不同的场景中，节点会采取不同的行为策略，以期获取更大的利益。

正常节点群体的策略分为两类:第一类是车辆节点愿意接收交通服务信息并转发，同时对于自身感知的信息愿意自主发布，第二类是车辆节点愿意接收交通信息并转发，但是不愿意自主发布交通信息。

自私节点群体的策略也分为两类：第一类策略是车辆节点接收交通服务信息并转发；第二类策略是车辆节点接收交通服务信息但并愿不转发。

恶意节点群体的策略同样分为两类:第一类是车辆节点接收交通服务信息，第二类是车辆节点拒绝接收交通服务信息。

在本模型中，影响节点采取合作行为的因素包括两大类：一是成本付出，例如自身能量消耗等；二是收益，包括节点信誉值等。在博弈模型中通过对成本收益的演化分析来激励车辆节点在信息服务传输中采取合作行为策略。在本文的研究中，车联网的网络结构除了各类车辆节点、路基设备，还包括一个可信认证中心。在一次交通信息传输过程中，当车辆节点对感知的交通信息主动发布或者对收到的信息进行转发，则认证中心对节点进行收益奖励。

2.2 群体策略集

因为在车联网中存在多个群体，交通信息传输的过程中存在群体之间的演化和博弈，不同群体具有不同的行为决策集合。

群体1的策略空间是G1={a1,a2},a1表示节点接收交通服务信息并转发，同时愿意自主发布相关服务信息，a2表示节点仅仅接收交通信息并转发，但是不愿意自主发布交通服务信息。

群体2的策略空间是G2={b1,b2},b1表示节点接收交通服务信息并转发，b2表示节点仅仅接收的交通服务信息，但拒绝转发。

群体3的策略空间是G3={c1,c2},c1表示接收交通服务信息，因为这些信息有可能对自身有用，c2表示拒绝接收。

2.3 收益计算

在本文的博弈模型中，车辆节点的收益可以定义为参与者采取某种具体的行为策略之后可以获取的收益。车辆节点的收益函数的计算如下：

节点的收益=每个节点接收交通服务信息获得的收益奖励+转发信息获得的收益奖励+自主发布交通服务信息获得的收益奖励-消耗的能量(转发能量消耗+自主发布能量消耗)。

由于车辆网中车辆节点是移动的，假设两个车辆节点之间的连接时间服从指数分布，在一段时间T内，两车的连接概率计算如式(2)所示

(2)

在群体1中，车辆节点选择策略a1的概率是x,x∈[0,1]；在群体2中，车辆节点选择策略b1的概率是y,y∈[0,1]；群体3中，车辆节点选择策略c1的概率是z,z∈[0,1]。

当群体1中的某个节点选择策略a1，则其获得收益的概率计算如式(3)所示

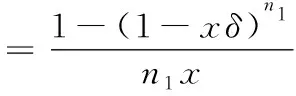
(3)

其中，n1为某次博弈过程中，群体1中参与博弈的节点的个数，δ为据式(2)计算的两车连接的概率值。

当群体2中的某个节点选择策略b1时，收益概率计算如式(4)所示，其中n2为某次博弈过程中，群体2中参与博弈的节点的个数

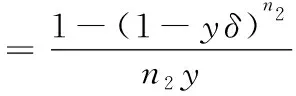
(4)

当群体3中的某个节点选择策略c1时，收益概率计算如式(5)所示，其中n3为某次博弈过程中，群体3中参与博弈的节点的个数

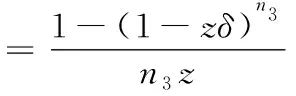
(5)

在计算出节点的收益概率之后，可以据此进行节点的收益的计算。

以群体1中的某节点为例，节点的收益CG1计算过程如式(6)所示

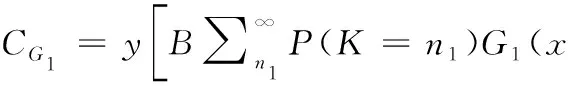
(6)

其中，B表示收益之和，L表示消耗能量之和。当节点选择策略a1时，B的值等于r1+r2+r3,L的值等于e1+e2+e3；当节点选择策略a2时，B的值等于r1+r2；L的值等于e1+e2。

同理，群体2中节点的收益CG2计算过程如式(7)所示

1.温度。保持舍内温度20℃左右，分娩后3 d内适宜温度32℃～28℃；4～7 d适宜温度28℃～25℃；8～30 d适宜温度25℃～22℃。在舍内设置保温箱，进行人工保温。

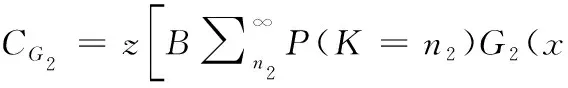
(7)

其中，当节点选择策略b1时，B的值等于r1+r2,L的值等于e1+e2；当节点选择策略b2时，B的值等于r1；L的值等于e1。

群体3中节点的收益CG3计算过程如式(8)所示

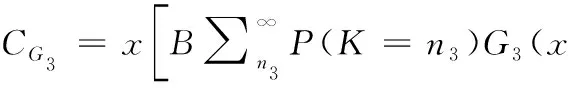
(8)

当节点选择策略c1时，B的值等于r1,L的值等于e1；当节点选择策略c2时，节点采取消极策略，即不进行任何接收或转发信息的行为，获得的收益奖励和消耗均为0，因此收益计算结果也为0。

依据上述节点收益的计算，可以计算各个群体的平均效用函数，以评估群体的博弈状况。依据式(6)，群体1的平均效用函数计算如式(9)所示

(9)

同理，依据式(6)，群体2的平均效用函数计算如式(10)所示

(10)

群体3的平均效用函数计算如式(11)所示

(11)

2.4 模型演化稳定策略分析

在这个多种群的演化博弈环境中，需要设计动态演化模型的演化稳定策略，该策略表明群体博弈最终趋于一个稳定状态。在本文的应用场景中，每个群中的个体节点在群的整体演化过程中都会进行自我学习，通过学习，选择收益较高的策略，放弃收益低的策略选择，逐渐的固化收益最大化的策略选择。在多次的动态博弈过程之后，整个群体趋向动态收敛直至达到均衡。演化策略的设计如下：

假设某次博弈的开始时刻为mt，结束时刻为，(m+1)t,m≥0。在一次动态演化博弈过程中，以正常节点群为例，当群体1中的节点选择存在如下计算过程

q[a1,∂a2+(1-∂)a1]≻q[a2,∂a2+(1-∂)a1]

(12)

其中，演化参数∂∈(0,1)，如果式(12)成立，则策略a1就是群体1的演化稳定策略。同理可以确定群体2和群体3的演化稳定策略。

通过上述步骤，车辆网中的车辆节点在动态演化博弈模型中经过演化，逐渐趋向选择收益高的策略，并且整个网络系统在多次演化后趋于一种稳定状态，从而实现抑制节点的自私行为，激励节点的合作行为，提高交通服务信息的传输效率。

3 实验及仿真结果分析

为了有效评估本文中提出的方法，以NS2仿真软件为平台，建立仿真环境，测试本文提出的模型在交通服务信息传输应用场景中的性能。

在本文的仿真实验中，各项实验参数设置如下：仿真区域大小为2500 m×2000 m，通信范围为160 m，车辆的速度依照目前国内城市道路主流限速状况以及日常交通流量情况，设置为30 km/h～65 km/h，仿真时间为100 s。当恶意节点占较大比例时，网络将处于失效状态，本文方法主要研究抑制自私节点的不合作行为，因此对于恶意节点占较大比例的情况不考虑。在本文的仿真实验中，车辆节点数目设置为300，设置正常节点和自私节点占总节点数的90%，其中正常节点数为180，自私节点为90个，恶意节点仅占10%。

在仿真实验中，群体1、群体2以及群体3在实验初始采取合作行为即分别选择策略a1,b1,c1的节点比例占各自所属群体节点总数比例为15%。依据文中对于节点收益和能量消耗的约定，经过多次实验，设置仿真实验中模型初始参数如下：收益参数r1=5,r2=7,r3=10，同时设能量消耗参数e3=4,e2=3,e1=2。

本文研究中，仿真实验分为两个部分，第一部分是对本文中提出的算法自身性能评估，第二部分是将本文方法与M.RAYA等[6]提出的方法进行比较，评估两种方法对网络性能的影响。

第一部分：图1为在仿真实验中随着时间的推移，群体1、群体2、群体3中的节点选择合作策略a1,b1,c1百分比变化。

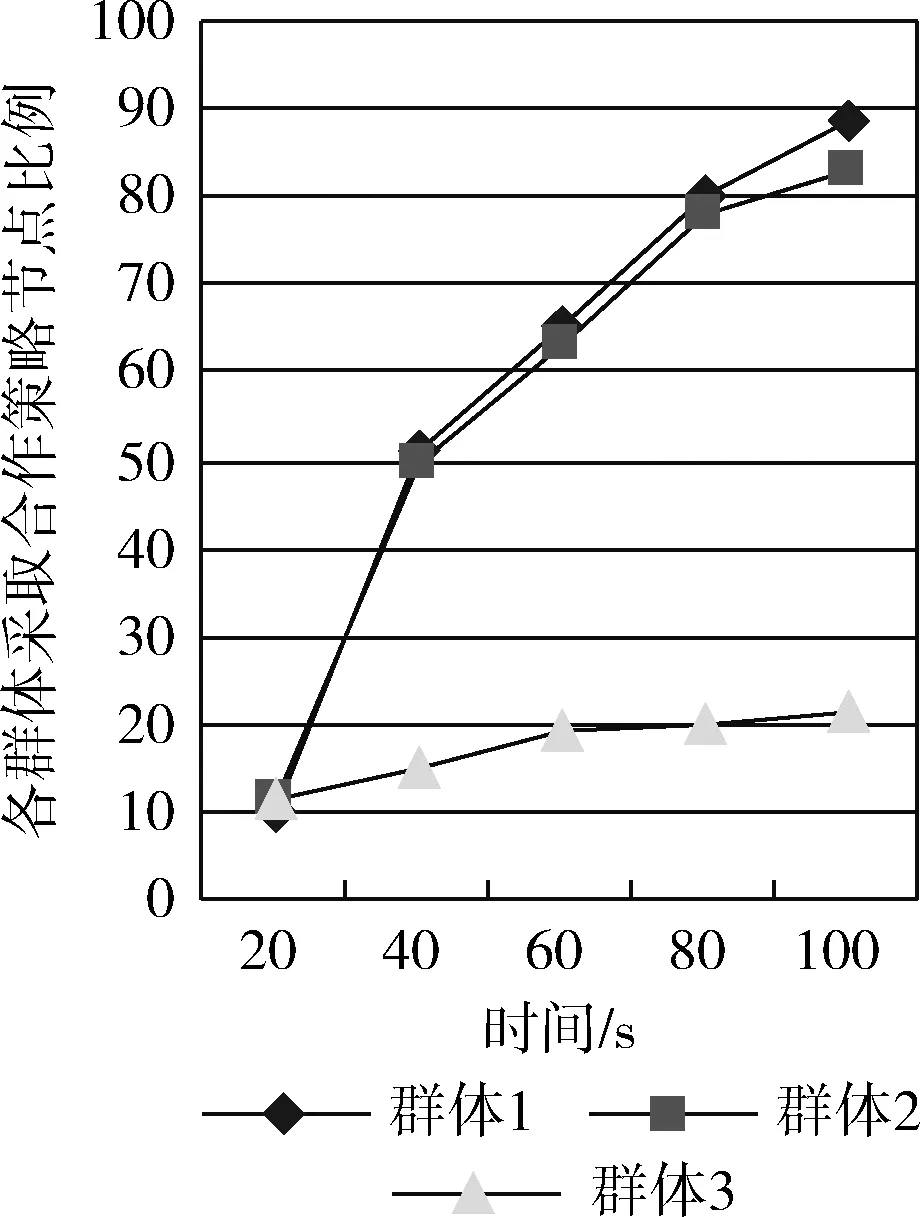
图1 选择合作策略的各种群节点百分比变化

图1表明，在模型中变量固定,即模型的激励确定的情况下，随着仿真实验的进行，模型展开演化博弈，各个群体中选择合作策略的节点占各自群体节点总数的百分比从初始时的10%陆续增加，并且随着时间变化，逐渐趋于稳定，表明系统经过多次博弈之后，趋于稳定状态，其中群体1和群体2中节点的百分比都接近89%。由于仿真实验设置中群体1和群体2节点的数量占网络中节点数据的百分比达到90%，因此当这两个群体的节点有接近89%的节点最终选择合作策略之后，整个网络将逐渐形成了一个大多数节点都选择合作策略的稳定的车联网网络环境。仅占整个网络节点10%的恶意节点所属群体3，在多次博弈后，选取合作策略的节点所占百分比同样有所增加，提高到约20%。

图1的结果表明随着仿真时间的推移，模型不断演化，仿真结果图中显示本文的激励机制是有效性，正常、自私和恶意3个群体中选择合作策略的节点数目在不断增加，并逐渐趋于稳定。

在现实应用中，自私节点的不合作行为对车联网中交通服务信息的传输产生较大的影响，在仿真实验中，将调整模型的收益参数，激励自私节点选择合作行为。设置通过当实验中能量消耗参数不变，同时发布收益奖励保持r3=10不变。在首次设置中，r2-e2=4，后续实验中我们逐次增加r2-e2的值d，即当节点转发交通服务信息时，获取的收益奖励与付出的能量消耗对比越明显，将会有效地激励节点更多参与网络中的信息转发。具体实验结果如图2所示。

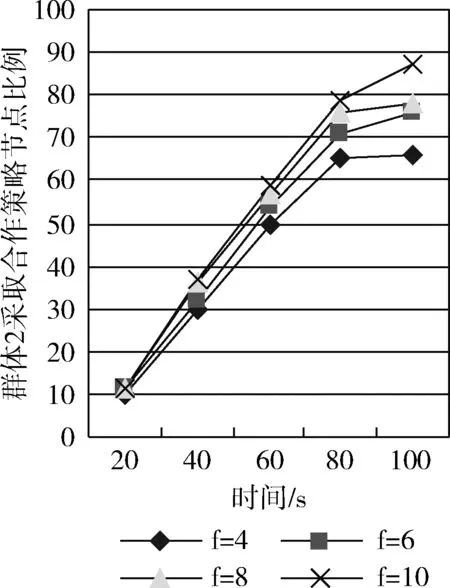
图2 转发收益变化对群体2合作策略选择的影响

当保持收益r1=5、r2=7不变，初次设置r3-e3=6，在后续中逐次增加r3-r1的值f，即当节点主动发布交通服务信息时，获取收益奖励与付出能耗对比越明显，则将激励节点更积极的主动发布服务信息。具体实验结果如图3所示。

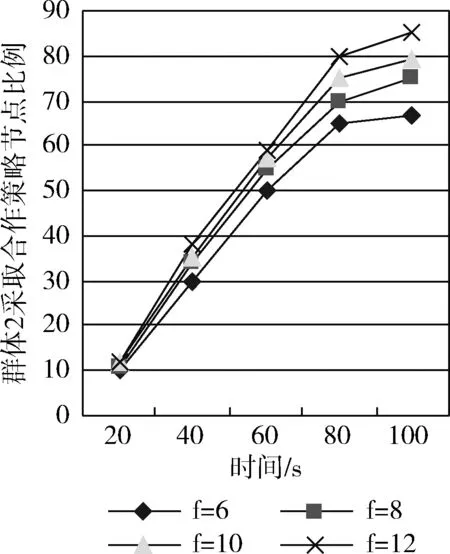
图3 发布收益变化对群体2合作策略选择的影响

图2和图3表明，群体2中的自私节点，在选择合作策略给自身带来的收益与能耗对比显著的激励机制下，该群体中的节点选择合作策略的百分比呈现出显著持续增长态势，并最终趋于一种稳定状态。实验结果显示，当博弈模型设置合适的收益参数时，能有效激励自私节点趋向选择收益较大的策略。

第二部分：对比本文方法和M.RAYA等文中提出的方法，从丢包率、转发率等性能指标对网络进行全面评估。本文方法中模型参数设置为初始设置状态，仿真时间为100 s。

图4表明本文方法的转发率在达到约90%后趋于稳定，而M.RAYA等文中方法虽然采取了重复广播的策略，但是由于节点的非积极合作行为产生的消极影响，导致转发率只维持在70%左右。

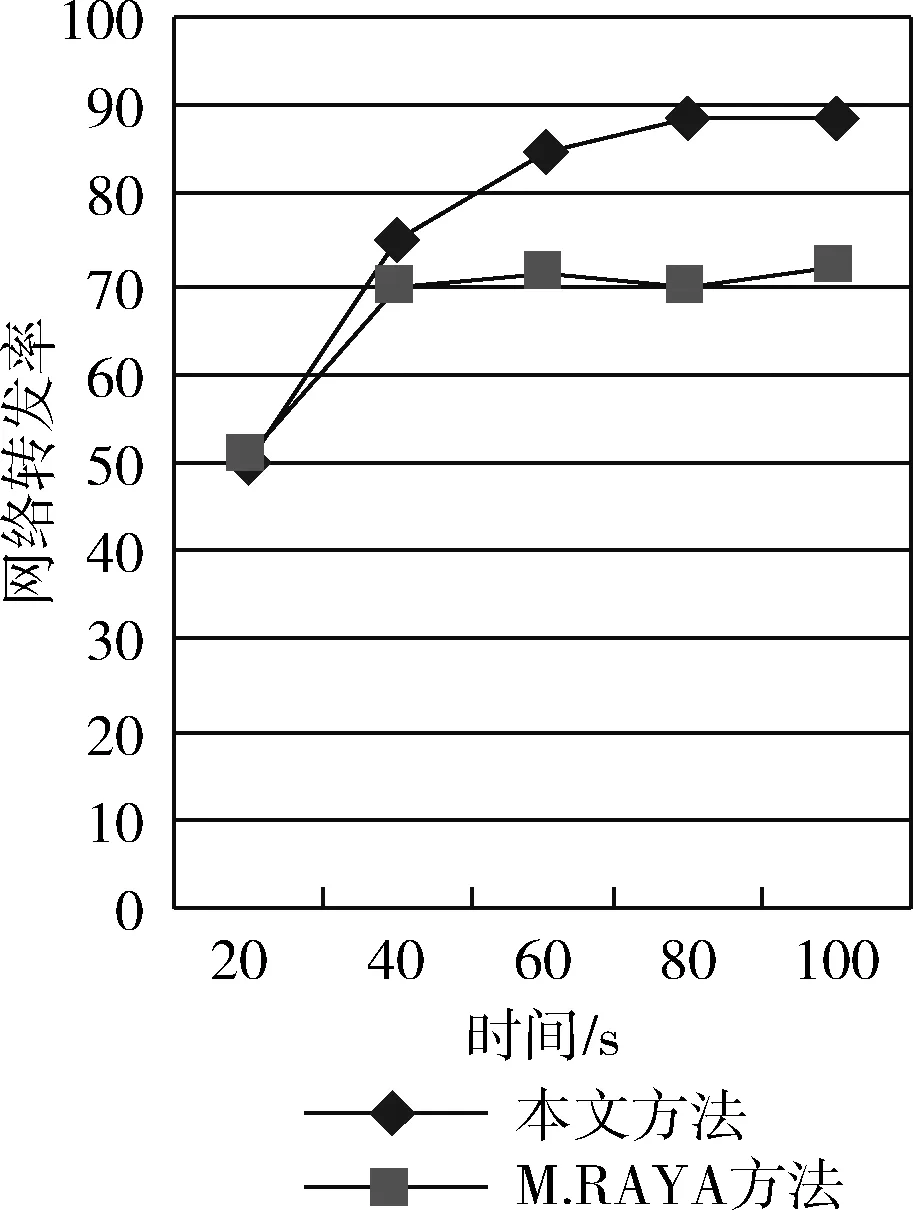
图4 两种方法网络转发率对比

图5中，在仿真初始阶段，由于节点参与数目较少，本文方法和M.RAYA方法的丢包率都约为20%左右。随着仿真时间的推移，越来越多的节点参与，M.RAYA方法由于自私节点和恶意节点的影响，网络的丢包率持续增长，接近35%，而本文的方法由于有效激励节点，随着仿真时间的推移，越来越多的节点选择合作策略，当博弈模型趋于稳定时，网络的丢包率也趋于稳定，保持在15%之下。

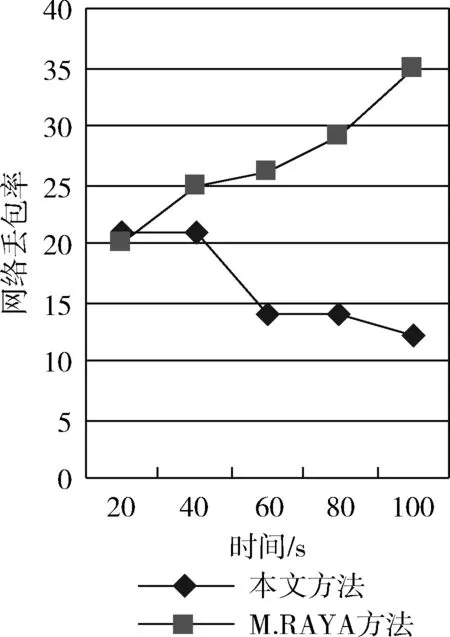
图5 两种方法网络丢包率对比

图4和图5的对比结果表明，通过激励机制鼓励节点采取合作策略后，本文的方法对网络性能的影响较为明显，与M.RAYA文中方法对比，仿真网络的转发率有显著提高，而丢包率则下降明显。

上述两部分的仿真实验结果表明，本文中提出的动态演化博弈模型，能有效地激励节点采取合作行为，抑制了自私节点的自私行为。

4 结束语

针对车联网环境中交通服务信息传输的应用场景，本文设计提出了基于博弈理论的动态演化模型。该模型针对车联网中正常节点群体、自私节点群体、恶意节点群体分别建立策略空间，通过多次演化博弈，激励节点采取收益最大化的合作行为策略，有效抑制了自私节点的自私行为，从而形成趋于稳定的良性的交通服务信息传输环境。在后续的研究中，将进一步对模型参数进行分析以优化模型，进一步提高模型的效率。