计算域对管内受限射流流动特性的影响

王曼宁 周宇 王梦影 王怡

西安建筑科技大学环境与市政工程学院

0 引言

对于受限空间传统的通风方式具有较低通风效率和能效比，射流通风有良好的气流组织，其中控制射流边界，合理地根据受限条件设计送风末端是提高射流通风效益的关键。如在锅炉管内焊接、烧结作业的情况，这类作业中往往存在着固定的高温散热源。受限空间结构作为外扰是干涉通风射流的因素，所以在现有受限条件下如何设置合理边界条件来提高或管道内通风效率是有效改善工作区局部环境、降低能耗的关键。

目前大多对管内受限射流流动研究主要应用于射流燃烧领域诸如燃烧室、反应器。管内射流的发展阶段通常分为过渡段、基本段、环流段、管流段四个主要过程，其中环流的产生和湍流特性对管内的传热、传质有很大影响[1]，因而一直为人们所重视和研究。赵烈[2]对柱形燃烧室内的轴对称等温射流流场进行了数值模拟，发现回流是这类流场的普遍特征。大多燃烧室被设计成突然扩张的外形，为的是产生回流区使热的燃烧物回流至火焰根部从而起到稳定火焰的作用。

在管内受限焊接通风类问题中入口流速较低且出口为大气压，为提高通风能效此时应避免出现管内射流回流区，需设定合理计算域并控制射流边界实现，故本文在传统管内受限射流的研究基础上进行通风数值模拟选取了三种计算域，探究低速、出口为大气压下受限射流特性。

1 基本方程及物理模型

对于本文等温射流作用下的管内受限问题中计算的基本控制方程为N-S方程，根据管内流场特性为定常，湍流模型采用RNG k-ε二方程形式，RNG k-ε湍流模型计算管内首先射流流动问题比标准的 k-ε方程可以更好地处理高应变率和流线弯曲程度较大的流动，即能模拟射流撞击、旋流以及二次流等复杂的流动问题，且对模拟这类问题具有较好的适用性[3]。

由时均法将瞬态N-S方程要求的变量分解为时均常量和变量。将及平均运算法则为时均速度为波动速度）代入N-S方程得到时均雷诺方程如下：

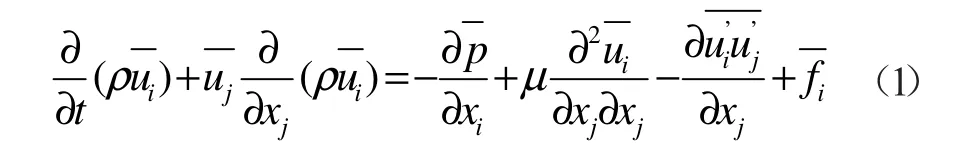
基本控制方程如下[4]：

连续性方程

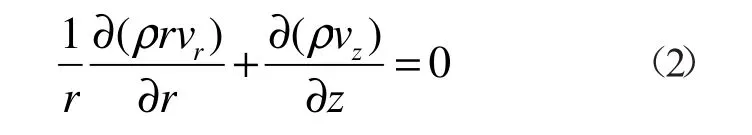
动量方程

r分量

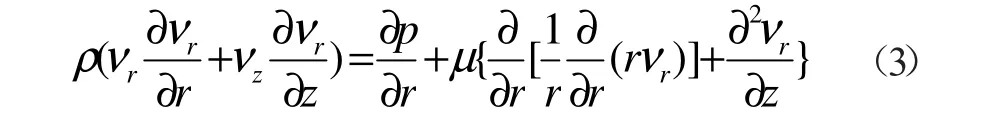
z分量

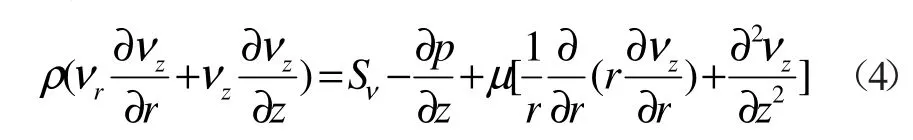
湍流动能方程（k方程）

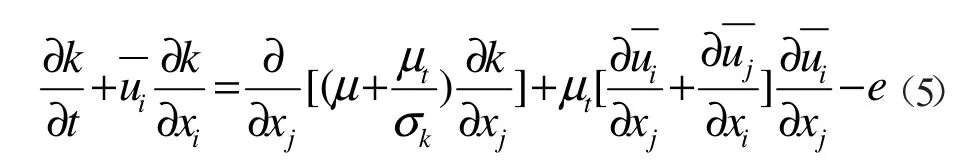
扩散方程（ε方程）

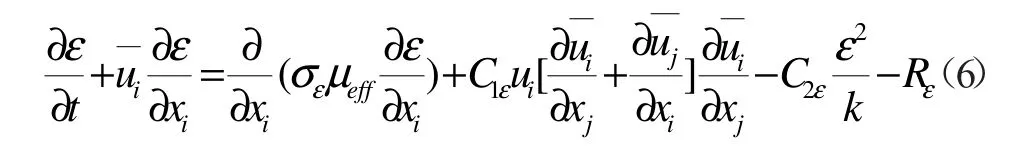
式中：Sv为源项；ρ为流体密度，kg/m3；P 为静压，Pa；μ为湍流粘性系数为湍流能扩散率ε 的普朗特数，取 1.3；η0=4.38；β=0.012；Cμ，C1ε，C2ε为经验常数分别取 0.09，1.44，1.92。

本文研究的是等温受限射流的轴对称流动。考虑射流的旋转但不计其化学反应，旋转轴对称物理模型如图1，显示了未扩展、圆筒域、锥筒域三种不同计算域形式。圆筒域、锥筒域采用Fluent中压力远场边界，将计算域边界扩大为出口边界的20倍，三种计算域采用相同平行流送风射流入口边界，为velocity-inlet，风速4m/s，方向沿x轴正向；出口边界为pressure-outlet；因未考虑人员操作位置和热源位置及温度，仅研究受限射流流场规律，故其余面均为绝热wall；格式simplc压力速度耦合方式，二阶差分，壁面处默认为非滑移边界条件。用二维模型进行数值模拟计算更为高效，求解器中space选择axisymmetric swirl，采用axis对称边界，二维模型由x坐标轴回转可产生三维回转体。

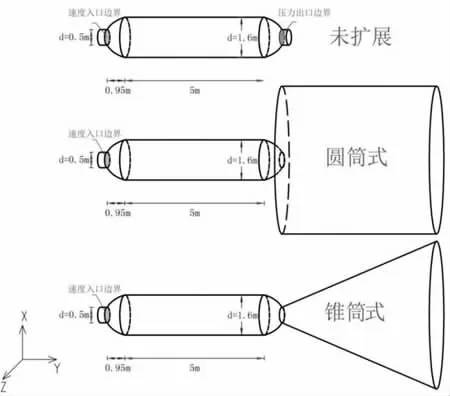
图1 三种计算域模型及尺寸图

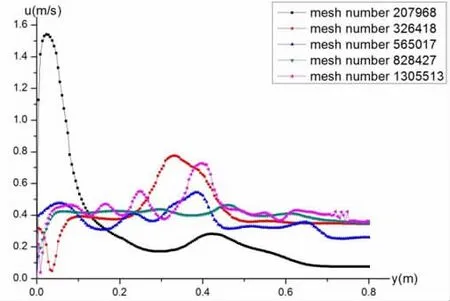
图2 不同数量网格下检测线速度分布

以未扩展计算域的二维物理模型为例进行网格无关性验证。如图2选取网格数为20万、32万、56万、82万、130万进行网格独立性分析，分别截取了各网格数量管中心垂直于轴线方向的一组监测点（y=0～0.8 m，x=3.45 m）的速度分布，可看出随着网格数量的增加，监测点上速度分布基本相同，说明计算结果的变化趋势已经比较接近，可认为此时网格的增加使得计算结果的变化非常小。从56万网格开始，流场的速度分布基本相近，说明计算结果的变化趋势已经比较接近，可认为此时网格数的增加并没有影响流场分布的不同，故选择56万的网格进行模拟。

2 模拟结果及分析

为研究出口为压力边界时采用Fluent中的远场边界，扩大计算域是否会影响管内流动情况本文采取两种结构形式扩大出口边界计算域（圆筒式和锥筒式），可见相同送风边界时，不论以哪种形式扩大出口压力边界计算域，管内射流流场均明显发生改变，如图3。管内射流既有自由射流又有进口段流动的某些特点，壁的存在造成压力梯度，压力梯度的存在改变了射流扩展的速率、边界层增长速率以及速度分布的形状。

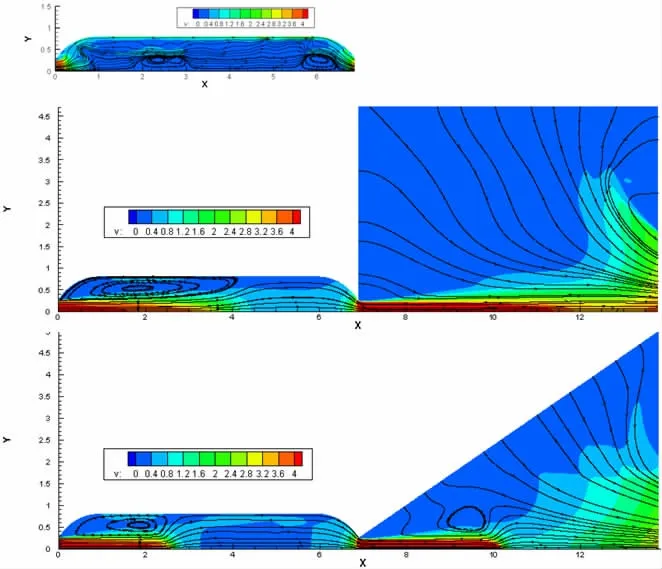
图3 三种计算域速度云图与流线图

图3显示了3种计算域下管内射流呈现的流动速度特征不一致，未扩展时可见入口速度在4 m/s时，靠近管中心2.3 m处最先产生回流漩涡，是由于射流卷吸周围流体，周围流体空间受限被射流卷吸后无来流补充，因此随之产生倒流而后射流沿管发展环流消失管中心流动大致平顺。同样距射流出口边界处由于射流结构受限也开始出现环流等大涡团运动。

圆筒式管中心流速增大，基本段势流范围为0～1.5 m，较未扩展（0～0.25 m）明显增大。射流基本段已经形成并向外扩展成环流段（1.5～3.8 m），周围流体被射流卷吸，外流速度减小，使流动方向的压力升高，故在受限射流中心上方存在涡旋。这是在射流扩展到管壁之前，所有外流的流体均被卷吸就产生涡旋的区域。射流以外不再作为势流，是由通过射流本身的再循环的流体所组成近似认为这一区域内压力不变。之后射流发展至管壁3.8～6.9 m，有相当大的压力梯度，截面上速度分布沿流动方向不断变化，直至发展成为充分发展的管流。

由于实际情况是射流在出口处突扩，故将扩展计算域改为锥筒式研究改变计算域的形状对管内流场的影响。在圆筒式基础上缩小了计算域，导致基本段势流范围也缩小。管中心射流发展的速度区域变短，即射流基本段和环流段均变短，管流段流场不如圆筒式计算域平顺。

三种计算域下的中心轴线速度衰减如图4，可见轴线速度衰减趋势基本一致。且相同受限结构形式和入口边界均影响射流基本段、环流及管流段。未扩展计算域时送风射流在送风入口处（x/d=4）射流就很快衰减，u/u0=0.08，会造成管内通风效率低，气流不能有效携带污染物，射流在管内基本失效。扩展计算域后（圆筒式、锥筒式）管内射流受限特征明显，存在基本段、环流段及管流段，且衰减过程在管内延长，圆筒式计算域送风射流表现更明显且衰减梯度小，携尘更有效。图5选取了整个管段内各典型截面沿流向的速度分布，对比了3种计算域下各截面射流形态，圆筒式从x=0.3 m至x=3.3 m管内截面速度分布发生改变，呈正态分布，也证明了扩展计算域计算的有效性。

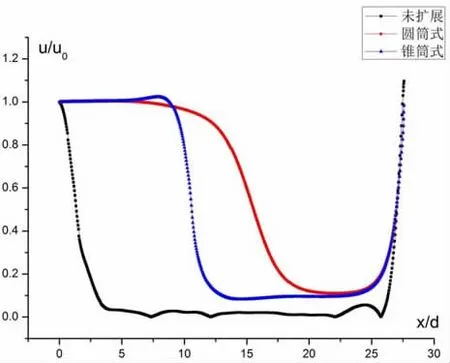
图4 射流中心轴线速度衰减无量纲图

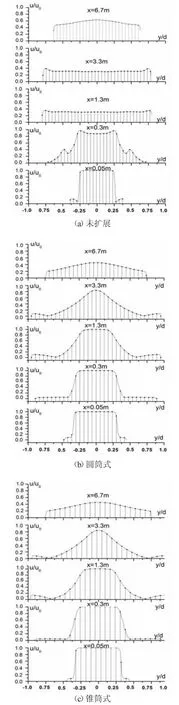
图5 管内射流沿流向速度分布无量纲图

3 结论

本文在平行流送风下选取三种不同计算域进行管内受限射流数值模拟，分析了射流入口基本段、环流段、管流段流动特征及衰减规律。采用远场边界证明了扩展计算域影响模拟结果的有效性及管内流速分布和中心轴线速度衰减位置及梯度变化，为设计风口改变射流送风方式优化管内通风奠定基础。