古建筑木结构透榫节点受力性能的影响因素分析
薛建阳,路 鹏,夏海伦
(西安建筑科技大学 土木工程学院, 陕西 西安710055)
古建筑木结构中的榫卯节点具有半刚性的连接特性,其可通过榫头和卯口之间的相互挤压变形及摩擦滑移减小外力作用,进而达到减震耗能的目的.徐明刚、董春盈、淳庆[1-3]等通过低周往复加载试验研究了不同榫卯节点模型的抗震性能,得到了节点的破坏形式、滞回曲线、骨架曲线及变形等性能;姚侃等[4]对采用燕尾榫连接的木构架模型进行了拟静力试验,研究其半刚性连接特性,并通过拟合得到了节点的恢复力模型;王俊鑫等[5]建立了反映木结构榫卯节点弯矩—转角关系的四参数幂函数曲线,揭示了榫卯结构的动力特性和耗能减震机理;谢启芳等[6]理论推导了燕尾榫节点的弯矩一转角关系,结合已有的试验结果,得到了节点的屈服点和极限点计算公式,并提出了燕尾榫节点弯矩一转角关系的双折线模型;隋等[7]根据木构架的低周反复试验结果,拟合得到了榫卯节点的弯矩-转角关系方程并建立了恢复力模型;Seo等[8]通过韩国的古建筑榫卯节点的静力及低周往复加载试验,分别得到了节点的荷载-位移曲线及滞回曲线,并提出了修正的节点双目标恢复力模型,同时给出了模型中各参数的建议值;Guan[9-10]通过试验与有限元分析相结合的方式,研究了日本常见的带木楔直榫节点,得到了不同尺寸及形状的木楔对节点的初始应力及抗推压性能的影响规律.
从现有榫卯节点的研究成果来看,大多以试验为主,且试验参数单一,试验未能考虑木材材料属性、摩擦系数等对节点力学性能的影响.本文建立了透榫节点的ABAQUS有限元分析模型,将分析结果与试验结果对比验证后,通过改变参数进行数值分析,研究了榫头高度变化、接触之间的滑动摩擦系数、木材材料性能以及轴压比等参数对透榫节点受力性能的影响.
1 透榫节点模型的建立
在建立有限元模型时,将榫卯节点材料性质简化为为正交各向异性,顺纹和横纹(径向和弦向)受压本构均采用双折线的理想弹塑性模型,受拉本构采用单折线模型,特征点由弹性模量与屈服强度等参数确定,取木材的抗拉弹性模量等于抗压弹性模量[12-13],如图1所示.
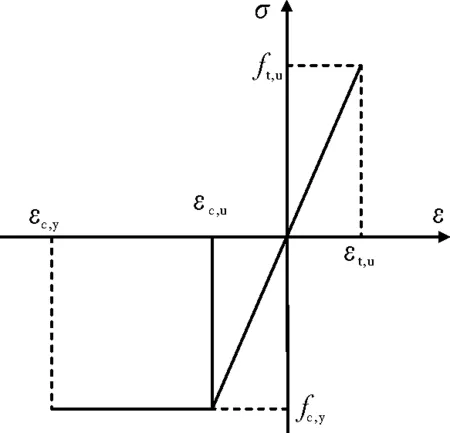
图1 木材顺纹及横纹应力-应变关系曲线Fig.1 The stress-strain curve of wood along the lines and horizontal stripe
在建立模型时,其弹性阶段与塑性阶段相关参数如表1所示.模型中构件的尺寸及构造按文献[11]中透榫节点试验所提供的尺寸取得,具体见表2及图2.
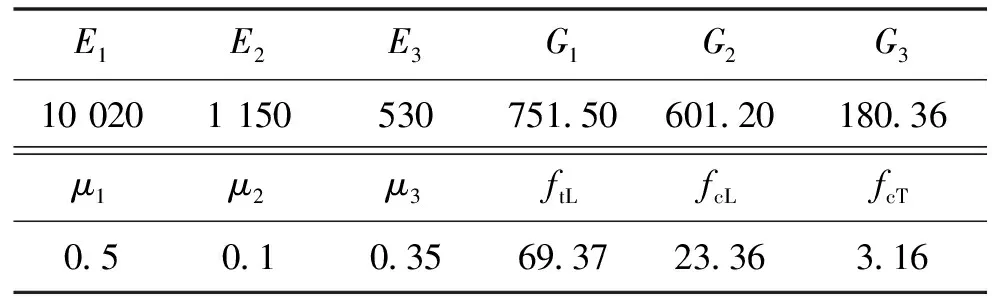
表1 木材主要参数指标Tab.1 The main parameter index of wood
注:E、G、μ、ftL、fcL、fcT分别为木材的弹性模量、剪切模量、泊松比、顺纹抗拉强度、顺纹抗压强度以及横纹抗压强度,表中弹性模量、剪切模量和材料强度的单位均为MPa;下标1、2、3分别表示木材中的纵向、径向和弦向.
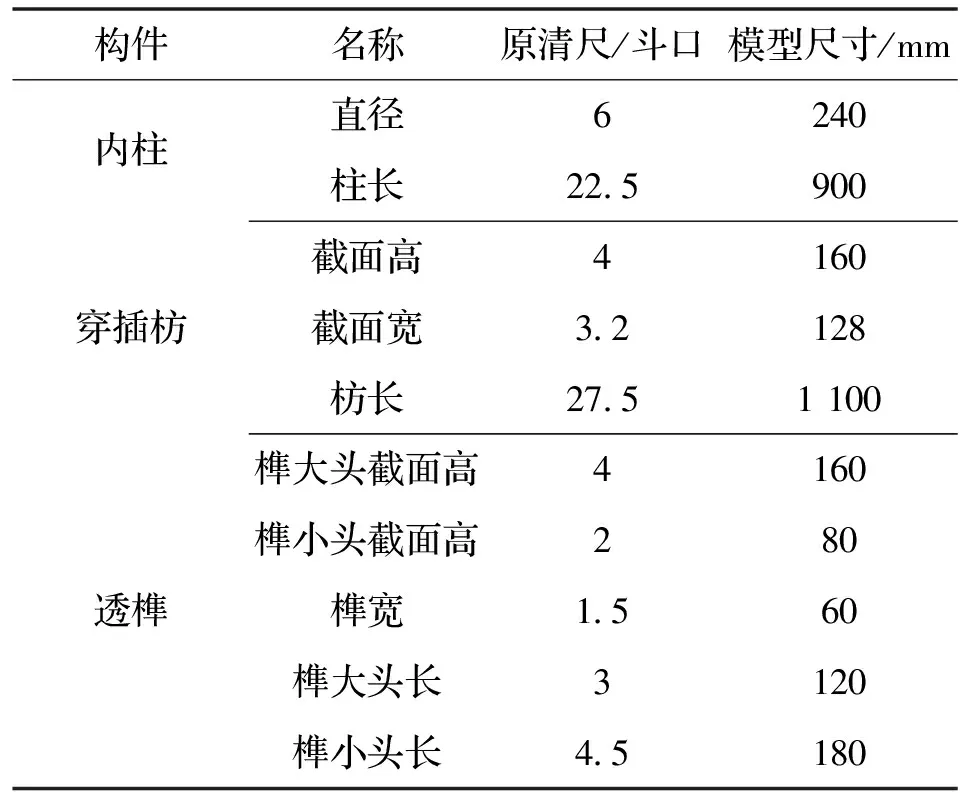
表2 透榫节点尺寸Tab.2 The sizes of through-tenon joints
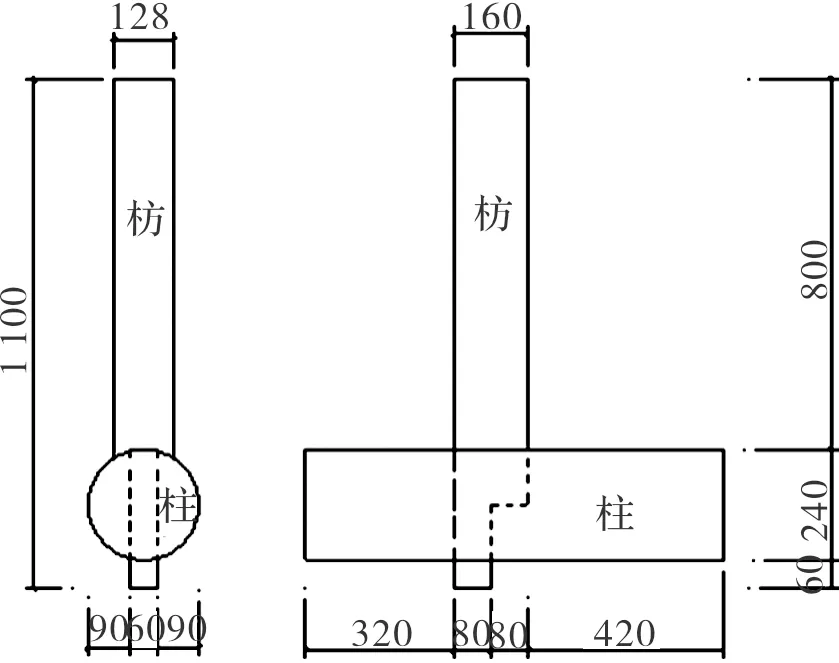
图2 节点模型尺寸示意(单位:mm)Fig.2 Sketch of model/mm
有限元模型中柱、枋的单元网格划分时,均采用六面体线性减缩积分单元C3D8R[14],网格尺寸为25 mm.当枋与柱之间产生接触时,采用库伦摩擦模型来考虑两个接触面之间的相互滑动,库伦摩擦模型用摩擦系数来表征两个接触面之间的相互摩擦,一般而言从静止状态进入到相对滑动时的静摩擦系数较相对滑动中的动摩擦系数大,摩擦系数的递增与滑动速度成指数递增关系.由于本次模拟为拟静力模拟,速度值不大,对摩擦系数的影响不大,所以根据已有的木材摩擦试验取摩擦系数为0.4.透榫节点模型在模拟中柱一端采用完全固结约束,另一端除轴向力加载方向外其余均固结约束;在柱的轴力加载端设置耦合点,施加轴向力;为避免加载时应力集中,在枋端水平位移加载处设置垫块,垫块的弹性模量为1×108 MPa,泊松比取0.2,在垫块前设置耦合点,并施加水平荷载.透榫节点网格划分、边界条件以及荷载施加示意如图3所示.
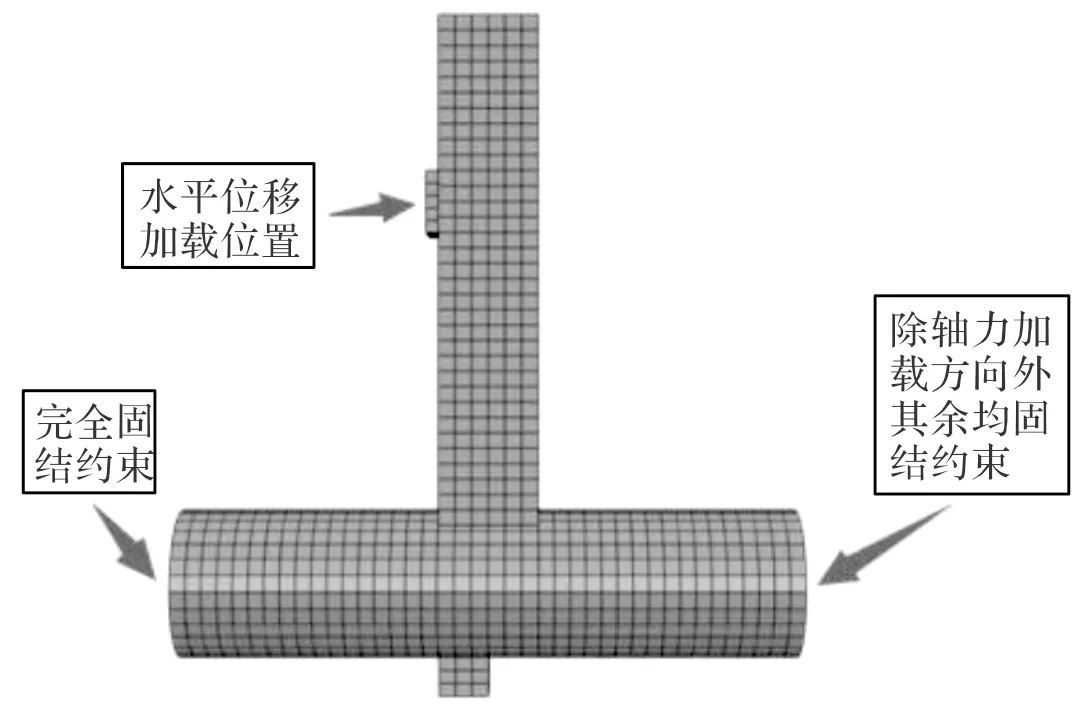
图3 透榫节点网格划分Fig.3 Model meshing of through-tenon joints
2 透榫节点模型的试验验证
文献[11]对透榫节点试件进行了水平低周反复加载试验,该透榫节点与本次模拟的节点尺寸以及所选用的木材均相同.试验时将柱水平放置,由千斤顶固定并施加轴向荷载,枋竖直放置,施加水平低周反复荷载,试验加载装置如图4所示.试验时作动器加载中心距柱上表皮的距离H=500 mm,以节点的极限位移为控制位移进行加载,根据计算确定控制位移值为50 mm.先以控制位移的10%、20%、30%、40%、50%依次进行一次循环加载,此后再逐级增大位移,每级位移下循环三次,直至试件破坏.
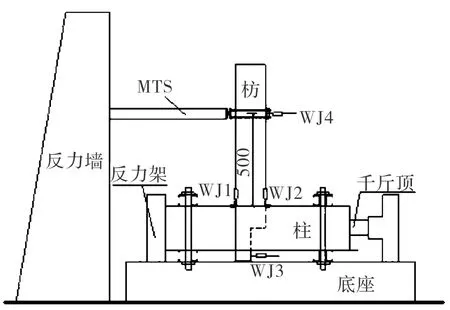
图4 试验加载装置Fig.4 Test setup
从透榫节点的低周反复试验获取的节点M-θ骨架曲线可看出,当正向加载转角为0.14 rad时,榫头受弯严重,榫头受拉侧的应力达到木材顺纹抗拉屈服强度,可认为节点发生弯曲破坏;当反向加载转角为0.13 rad时,榫头变截面处木材顺纹撕裂,可认为节点发生破坏.故本文在模拟分析时,取正向加载极限转角为0.14 rad,反向加载极限转角为0.13 rad,极限转角所对应的弯矩为极限弯矩.屈服弯矩采用通用屈服弯矩法获得,其对应的转角为屈服转角.将模拟得到的透榫节点的骨架曲线和主要参数与文献[11]、文献[15]中试验结果进行比较,分别如图5、表3所示.
从图5可以看出,模拟的骨架曲线没有出现下降段,这主要与模拟分析时所选择的材料应力—应变关系有关.模拟结果的荷载值比试验值偏大,主要是由于木材为各向异性材料且不完全均质,导致试验数据的离散性较大.此外,木材本身有初始缺陷,节点制作及安装也存在有偏差,而有限元计算未能考虑到这些情况.从图5及表3分别可以看出,有限元分析与试验得到的骨架曲线整体变化趋势基本一致、主要特征点的数值的误差在合理范围内,二者吻合较好.
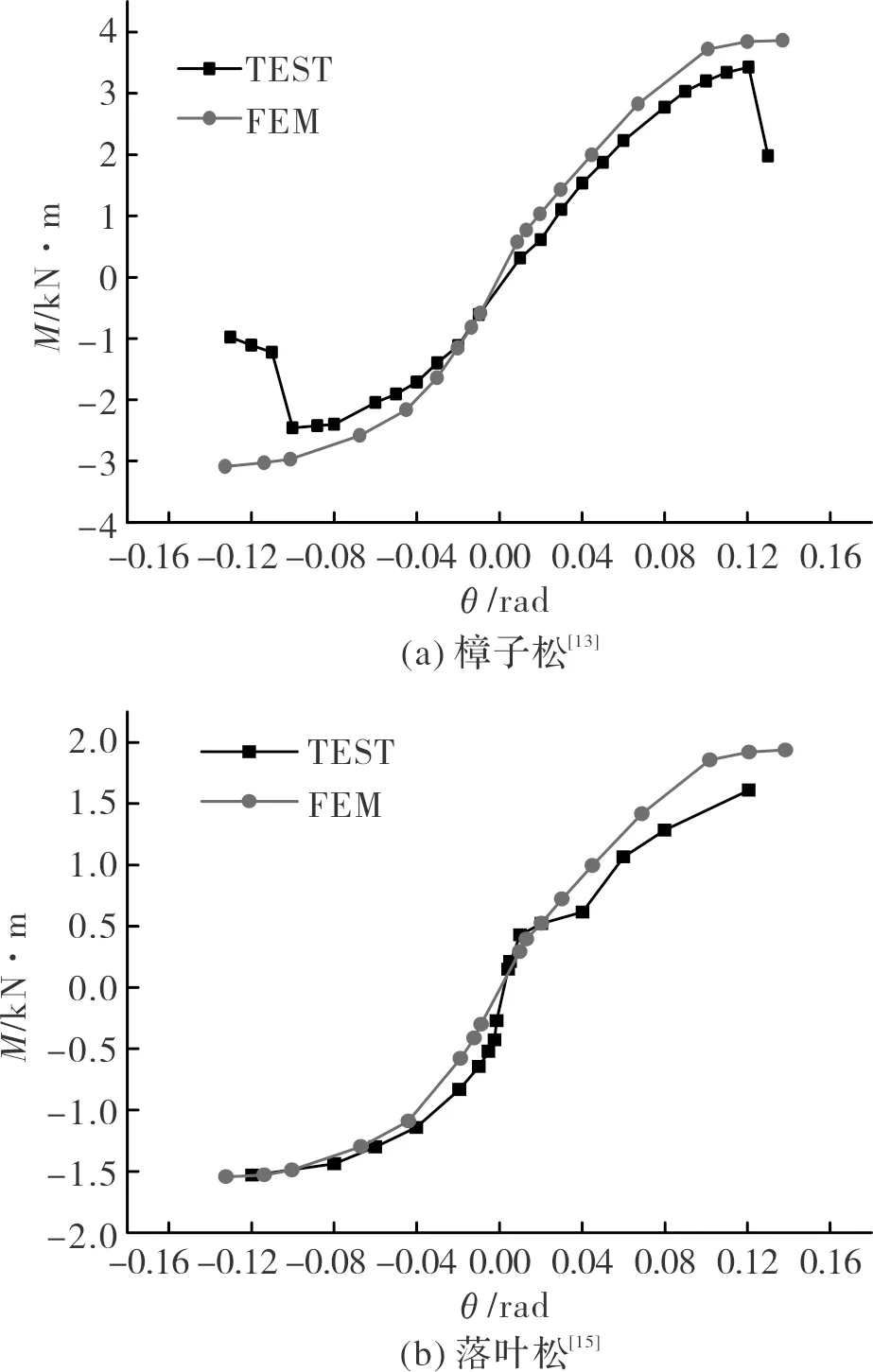
图5 透榫节点骨架曲线对比Fig.5 Comparison of skeleton curves of through-tenon joints between test and computation
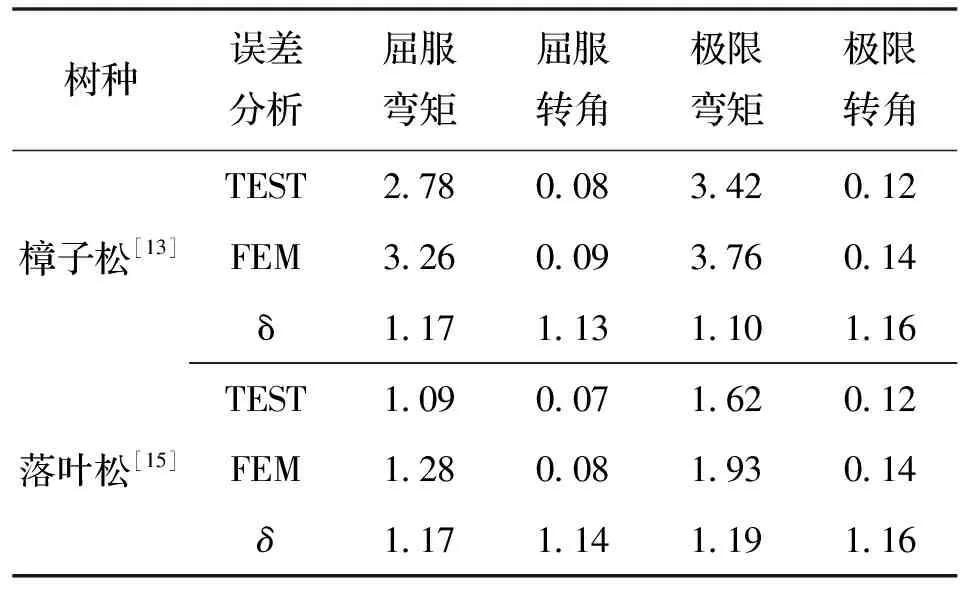
表3 主要特征参数比较Tab.3 Comparison of Main parameters
注:表中弯矩单位为kN·m,转角单位为rad,TEST表示试验值,FEM表示有限元计算值;δ为有限元模拟值与试验值的比值.
3 节点力学性能的影响参数分析
透榫节点受力性能的影响因素主要有节点尺寸、木材间摩擦系数、木材的材料属性以及轴压力等.因此,本文选取榫头的截面高度、摩擦系数、木材的横纹弹性模量、顺纹弹性模量、顺纹抗拉强度及轴压比等参数进行分析,通过逐个改变有限元模型的相关参数来分析其对透榫节点受力性能的影响.
3.1 榫头高度
其它参数不变,通过改变榫头截面高度h来研究其变化对透榫节点受力性能的影响,榫头高度分别取为120 mm、140 mm、160 mm、180 mm、200 mm,依次进行有限元分析.
图6给出了榫头高度变化对透榫节点弯矩-转角关系的影响,可以看出:榫头高度变化对榫卯节点骨架曲线的影响较为明显,在加载过程中,骨架曲线均随着榫头高度的增大而逐渐变陡,即在弹性阶段与强化阶段节点的刚度随着榫头高度的增大而增大.结合表4可知,随着榫头高度的增大,透榫节点的屈服转角有增大趋势,但不是很明显;屈服弯矩与极限弯矩均大幅度增大,尤其当榫头高度为200 mm时,节点的极限弯矩增幅最大,为80.483%.
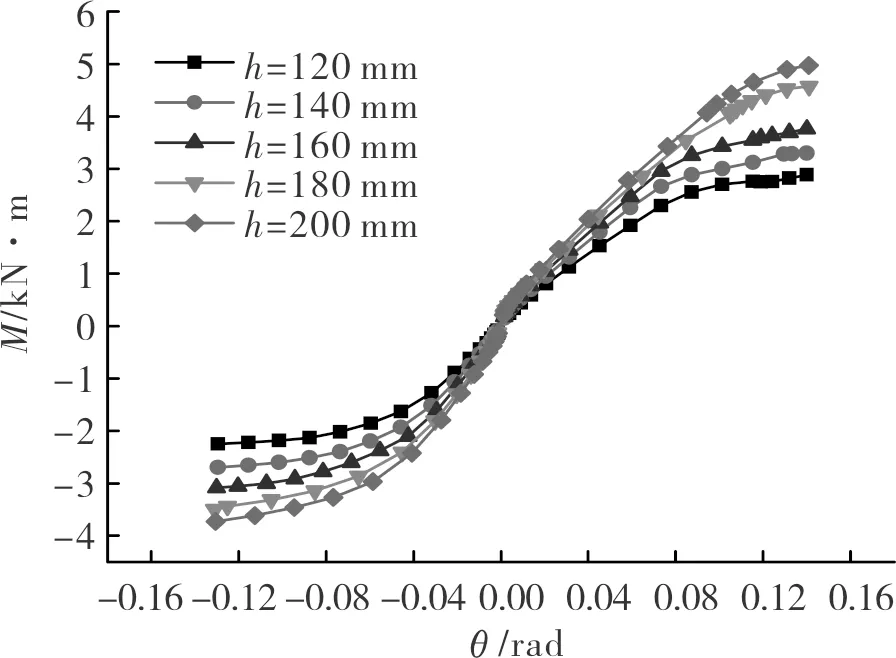
图6 榫头高度对节点弯矩-转角关系的影响Fig.6 Effect of mortise height on the relationship of moment-rotation of joint
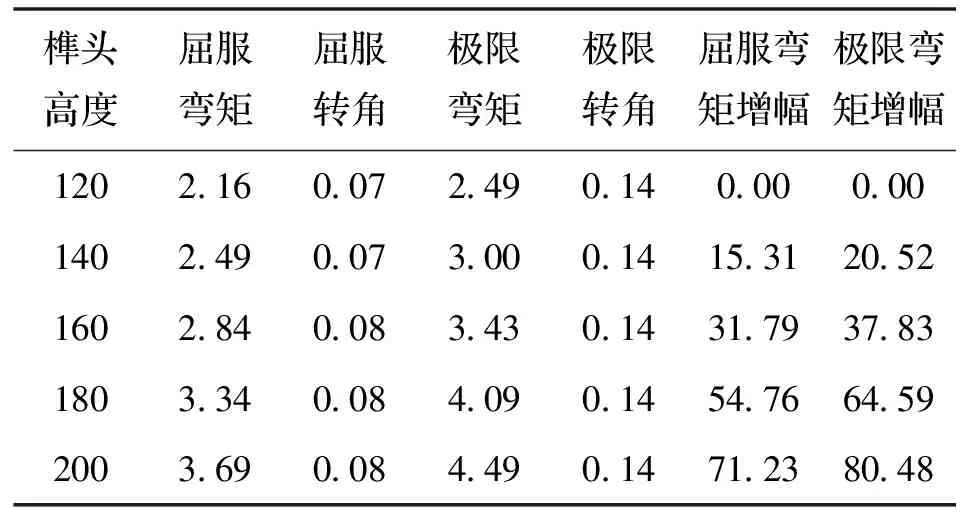
表4 榫头高度对承载力与变形能力的影响Tab.4 Effect of mortise height on bearing capacity and deformability
注:表中榫头高度单位为mm,弯矩单位为kN·m,转角单位为rad,弯矩增幅=|(Mi-M1)/M1|×100,Mi为表中第i行弯矩值,i=1,2,3,4,5.
3.2 摩擦系数
木结构构件做工的精细程度直接决定了榫卯节点接触面间的粗糙程度,从而导致摩擦作用的不同.构件做工越粗糙,榫头和卯口间的滑动面越粗糙,摩擦系数就会越大,接触面之间产生滑移所需要的荷载就越大,进而影响透榫节点在加载时的峰值荷载.保持其它参数不变,改变摩擦系数来研究其对节点受力性能的影响.木材的摩擦系数一般在0.1~0.6范围内,本文依次取摩擦系数μ为0.1、0.2、0.3、0.4、0.5进行分析.结果如图7、表5所示.
从图7和表5中均可以看出,透榫节点的刚度、屈服转角、屈服弯矩以及极限弯矩均随摩擦系数的增大出现不同程度的增大,其中弹性阶段和强化阶段刚度的增加均不是很明显;屈服转角增大显著;屈服弯矩的增长幅度明显大于极限转角的增长幅度.
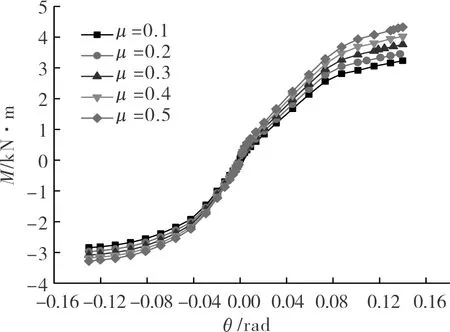
图7 摩擦系数对节点弯矩-转角关系的影响Fig.7 Coefficient of friction effect on the relationship of moment-rotation of joint
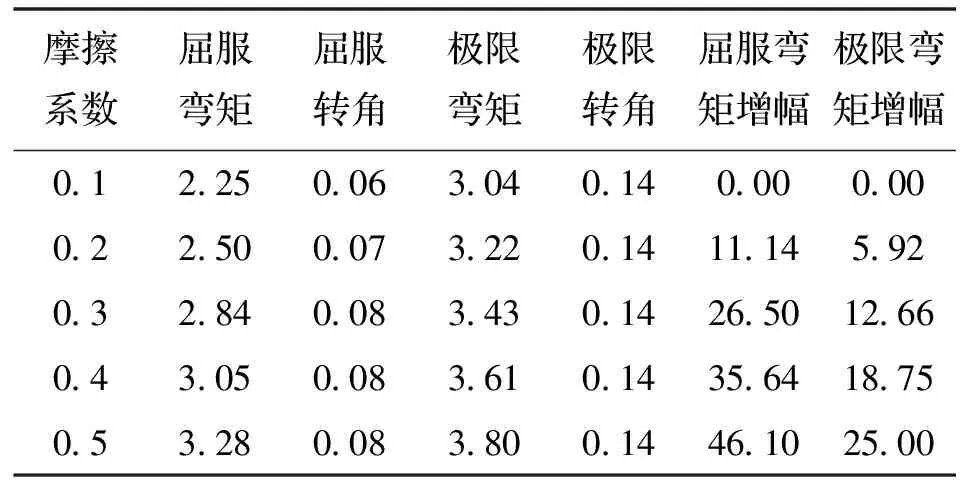
表5 摩擦系数对承载力与变形能力的影响Tab.5 Effect of friction coefficient on bearing capacity and deformability
注:表中弯矩单位为kN·m,转角单位为rad,弯矩增幅=|(Mi-M1)/M1|×100,Mi为表中第i行弯矩值,i=1,2,3,4,5.
3.3 横纹弹性模量
木材的顺纹抗压强度远大于横纹抗压强度,在节点受力变形过程中,榫头主要发生横纹受压变形.因此,有必要分析木材横纹抗压弹性模量对节点变形的影响.保持其它参数不变,分别选取木材横纹径向抗压弹性模量为0.50Ec、0.75Ec、1.00Ec、1.25Ec、1.50Ec进行分析.木材横纹弹性模量对透榫节点力学性能的影响如图8、表6所示.
从图表中可以看出,随着木材横纹弹性模量的提高,弹性阶段刚度增大,而在强化阶段,不同横纹弹性模量下的骨架曲线几乎平行,即横纹弹性模量对刚度几乎无影响;另外,随着横纹弹性模量的增大,透榫节点的屈服转角逐渐变小,屈服弯矩和极限弯矩逐渐增大,而且极限弯矩的增大幅度大于屈服弯矩的增大幅度.

图8 横纹弹性模量对节点弯矩-转角关系的影响Fig.8 Compressive modulus of elasticity effect on the relationship of moment-rotation of joint
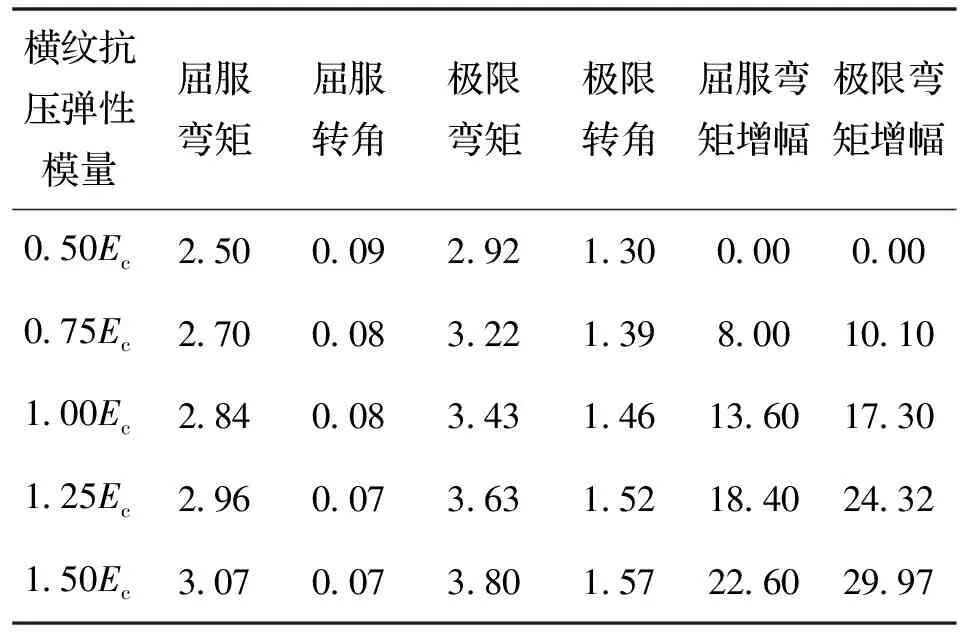
表6 横纹弹性模量对承载力与变形能力的影响Tab.6 Effect of compressive modulus of elasticity on bearing capacity and deformability
注:表中弯矩单位为kN·m,转角单位为rad,弯矩增幅=|(Mi-M1)/M1|×100,Mi为表中第i行弯矩值,i=1,2,3,4,5.
3.4 顺纹弹性模量
从理论来看,尽管木材的顺纹抗压弹模模量Et远大于横纹的,在受力时顺纹方向发生的变形较小,但其对节点受力性能的影响还不明确.为了研究不同顺纹抗压弹性模量对节点受力性能的影响,本文分别选取顺纹抗压弹性模量为0.50Et、0.75Et、1.00Et、1.25Et、1.50Et进行分析,结果如图9所示.
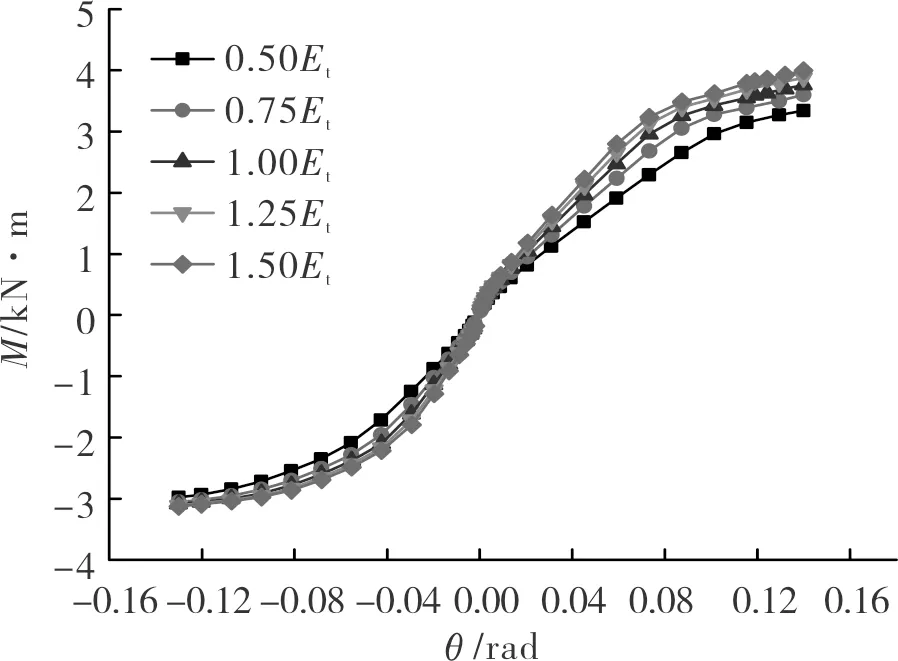
图9 顺纹弹性模量对节点弯矩-转角关系的影响Fig.9 Tensile modulus of elasticity effect on the relationship of moment-rotation of joint
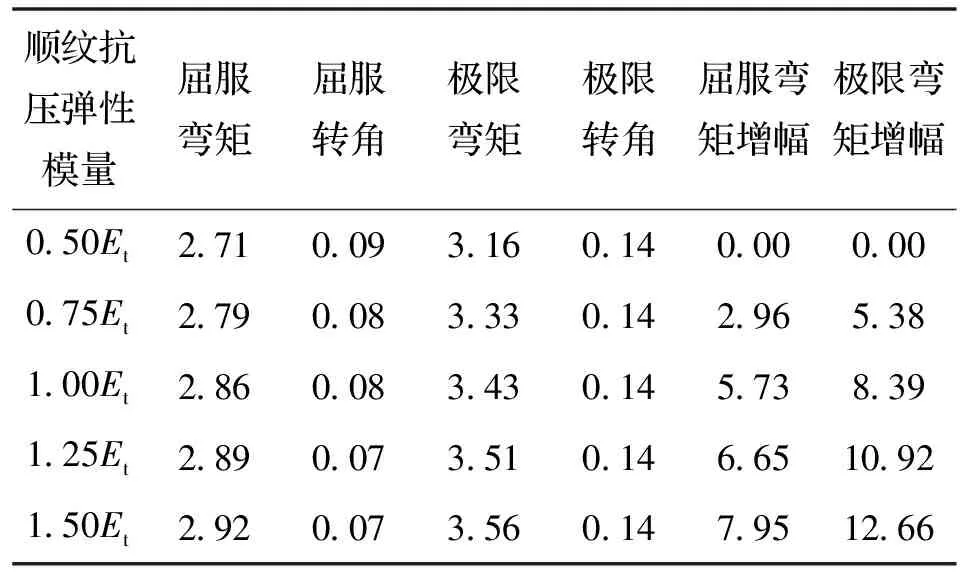
表7 顺纹弹性模量对承载力与变形能力的影响Tab.7 Effect of tensile modulus of elasticity on bearing capacity and deformability
注:表中弯矩单位为kN·m,转角单位为rad,弯矩增幅=|(Mi-M1)/M1|×100,Mi为表中第i行弯矩值,i=1,2,3,4,5.
从图9中可以看出,随着木材顺纹抗压弹性模量的提高,节点在弹性阶段的刚度逐渐增大;强化阶段的刚度随着顺纹弹性模量的提高有减小趋势;此外,随着顺纹弹性模量的增大,透榫节点屈服转角逐渐减小,屈服弯矩和极限弯矩均有不同程度的提升,但是提升并不显著,具体增幅见表7.
3.5 顺纹抗拉强度
木材的强度直接影响节点整体的力学性能,从透榫节点的试验结果来看,正向加载时,节点发生受弯破坏即顺纹受拉屈服.因此有必要研究木材顺纹抗拉强度ft对节点受力性能的影响.保持其它参数不变,分别取顺纹抗拉强度为0.6ft、0.8ft、ft、1.2ft、1.4ft进行分析,结果如图10所示.
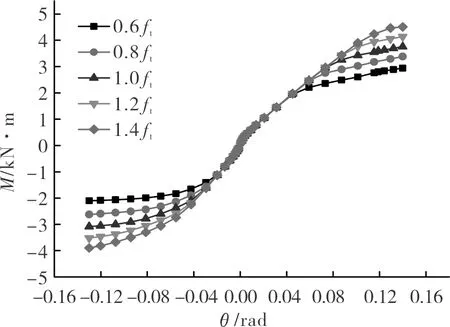
图10 不同顺纹抗拉强度下节点弯矩-转角曲线Fig.10 Tensile strength effect on the relationship of moment-rotation of joint
从图10可以看出,弹性阶段透榫节点的骨架曲线基本重合,而在强化阶段,随着顺纹抗拉强度的提高,骨架曲线的斜率有所变大,但是变化并不显著,即顺纹抗拉强度的改变对透榫节点弹性阶段与强化阶段的刚度几乎无影响.
随着木材顺纹抗拉强度的增大,透榫节点的屈服、屈服弯矩和极限弯矩均有明显增大.通过特征点的计算结果对比来看,节点的屈服弯矩的增大幅度大于极限弯矩的增大幅度,具体对比结果如表8所示.
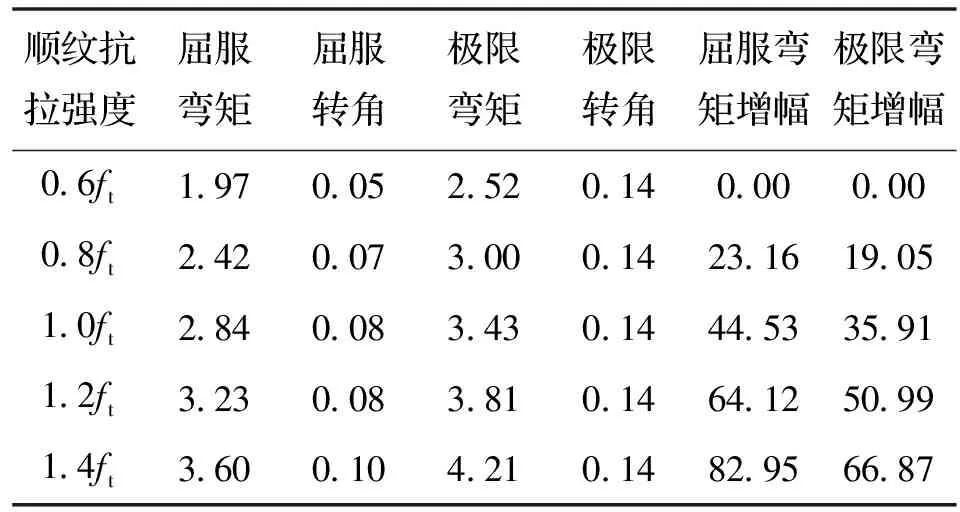
表8 顺纹抗拉强度对承载力与变形能力的影响Tab.8 Effect of tensile strength on bearing capacity and deformability
注:表中弯矩单位为kN·m,转角单位为rad,弯矩增幅=|(Mi-M1)/M1|×100,Mi为表中第i行弯矩值,i=1,2,3,4,5.
3.6 轴压比
根据现代结构理论,柱(墙)的轴向力的变化会影响结构的延性,通常由轴压比反映.尽管木结构建筑的高度较低,质量较轻,轴压比对其的影响可能较小,但轴压比对节点受力性能的影响并不明确.因此,本文通过改变柱顶施加的轴向力来研究其对节点受力性能的影响,保持其它参数不变,分别选取轴向力N为10 kN、20 kN、30 kN、40 kN进行分析,结果如图11所示.
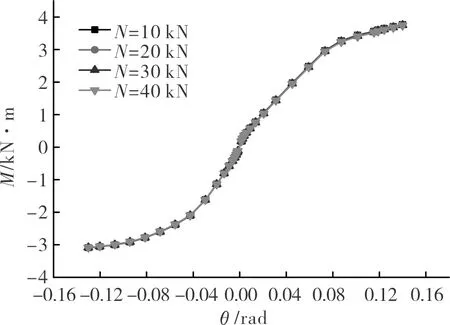
图11 轴压比对节点弯矩-转角关系的影响Fig.11 Axial compression ratio effect on the relationship of moment-rotation of joint
由于榫卯连接具有半刚性的特性,节点在受力过程中主要通过榫头与卯口的挤压变形提供抵抗力.从理论上分析,当对柱施加的轴向压力增大时,柱子会发生变形从而引起卯口变形,使得节点挤压紧密,会提高节点的承载力或刚度.但从图11显示的结果来看,改变轴向压力并未对透榫节点的弯矩-转角关系产生明显影响,即轴向力对节点的受力性能几乎没有影响.这是因为木材的顺纹抗压强度和弹性模量均较大,在柱顶施加的轴向力较小,不足以使卯口产生明显的变形,更不会使节点间的挤压紧密,从而不会影响到整个节点的受力性能.
4 结论
通过有限元分析程序ABAQUS对透榫节点进行建模分析,研究了榫头高度、榫头和卯口接触面间的摩擦系数、木材材料性能以及轴压比等参数对透榫节点受力性能的影响.主要得到以下结论:
(1)透榫节点在弹性阶段与强化阶段的刚度随榫头高度与摩擦系数的增大,均有不同程度的提高;随着横纹弹性模量、顺纹弹性模量的提高,透榫节点弹性阶段的刚度有所提高,而横纹弹性模量对强化阶段节点刚度几乎无影响;随着顺纹弹性模量的提高,强化阶段节点刚度有所降低;改变顺纹抗拉强度对节点所有阶段的刚度几乎无影响.
(2)榫头高度、摩擦系数、顺纹抗压弹性模量、横纹抗压弹性模量以及顺纹抗拉强度的增大,均使得节点的屈服弯矩和极限弯矩发生不同程度的提高.榫头高度、摩擦系数与顺纹抗拉强度的影响尤为显著;随着榫头高度、摩擦系数以及顺纹抗拉强度的提高,透榫节点的屈服转角有所增大,而随着顺纹弹性模量、横纹弹性模量的提升,透榫节点的屈服转角减小.
(3)在一定范围内,轴压比对透榫节点受力性能几乎无影响.

