基于AHP的SMOTEBagging改进模型

[电子科技大学 成都 611731]

Bagging是一种集成学习模型，它将多个分类器的预测结果进行集成，得到相比于单个分类器更稳定更准确的预测结果，有着广泛的应用[1～2]。在实际应用过程中，常常会面临数据不平衡的问题，比如信用风险预测中，违约用户的数量是远少于正常用户的数量的，在病情诊断中，检查呈阳性的样本数量总是少于呈阴性的样本数量。在这些应用中，少类样本往往才是最重要的样本[3～4]，传统分类模型会倾向于将样本预测为数量较多的那一类样本，导致对少类样本的预测准确率较差[5]。Bagging模型不能直接用于处理不平衡数据[6～7]，因而各种改进算法被提出，如Asymmetric Bagging[8]、RUSBagging[9]、SMOTEBagging[10]等，它们通过抽样的方法改变基分类器训练集中样本的分布，来提高Bagging对少类样本的预测能力。

本文将研究的重点放在对SMOTEBagging模型的改进上，一是为了在不牺牲模型整体表现的前提下，在SMOTEBagging的基础上进一步提高对少类样本的预测准确率（TPR），二是为了能减小集成规模，用更少的基分类器达到和SMOTEBagging一样甚至更好的表现，提高预测速度，减少模型在实际应用中对计算资源的占用量。为了实现这两个目标，本文将AHP方法引入SMOTEBagging中，构建了一种改进的SMOTEBagging模型，称之为AHPBased Bagging模型，并在27个属于不同应用背景的不平衡数据集和三种不同的基分类器设置下对AHPBased Bagging和SMOTEBagging在TPR、F1-Measure、G-mean和AUC上的表现进行了对比。

一、相关研究

在数据不平衡问题中，如何提高模型对少类样本的分类准确率，同时又不对其他样本的预测效果造成较大的负面影响，是研究者需要解决的主要问题[11]。为了提高Bagging模型在不平衡数据集下的表现，尤其是对少类样本的预测表现，研究者使用了不同的方法来调整基分类器训练集中的样本分布。Guo-Zheng Li[8]提出的Asymmetric Bagging模型用Bootstrap的方法，从多类样本中抽取和少类样本数目相同的样本，再和所有少类样本一起构成样本分布平衡的基分类器训练集。Xiaofeng Shi[9]为了解决脑电图中P300信号检测中所存在的样本不平衡问题，使用随机下采样方法（Random Under-Sampling）从多类样本和少类样本中各自抽取S/2个样本，构成大小为S的基分类器训练集。Liu[12]提出了EasyEnsemble方法，使用随机下采样方法从多类样本中抽取和少类样本数目相同的样本，然后与所有少类样本进行合并，构成基分类器的训练集。Shuo Wang[10]为了研究抽样方法对基分类器多样性及Bagging最终表现的影响，提出了UnderBagging、OverBagging和SMOTEBagging三种Bagging模型，UnderBagging和OverBagging采用Bootstrap的方式对每一类样本进行上采样或者下采样，使基分类器的训练集中的各类样本数相同，SMOTEBagging模型中用SMOTE方法来生成新的少类样本，调整基分类器训练集的样本分布。

在这些研究中，除了SMOTE方法外，其他都是用Bootstrap或者随机抽样的方法对样本进行上采样或者下采样，来构成样本平衡的基分类器训练集。但下采样会丢失大量与多类样本相关的信息，上采样会对少类样本进行多次重复采样，容易造成过拟合[13]，而由Charles[14]提出的SMOTE方法基于K近邻算法合成新的少类样本，则能避免这些问题，同时Shuo Wang[10]的研究发现，通过SMOTE方法来构造基分类器训练集能够提高Bagging中基分类器的多样性，因此在不平衡数据集上，SMOTEBagging在少类样本的TPR和F-Value上都有着比OverBagging更好的表现。Hanifah等[15]将SMOTEBagging用在个人信用风险的预测中，发现其在AUC和少类样本的准确率上都有较好的表现。因此本文以SMOTEBagging模型作为改进的对象。

AHP也叫层次分析法，由美国运筹学家Saaty[16]在20世纪70年代提出，是一种定性与定量相结合的决策分析方法，能够帮助决策者将复杂的多属性决策问题分解为单个指标下的两两成对比较问题，从而选出符合决策者需求的方案。有研究者将AHP方法引入了Bagging模型中，László[17]认为用AHP方法来计算基分类器的权重并进行组合能够得到更稳定的分类表现，但其准则层中只有错误率这一个指标。受到该文章的启发，本文将AHP方法引入到SMOTEBagging模型中，并在准则层中考虑了多个评价指标来评判基分类器的重要性。

二、AHP-Based Bagging模型

（一）构建思想

在Bagging算法中，训练出多个基分类器会有不同的表现，考虑如图1所示的3种基分类器，它们在6个关键指标上的分类表现如表1所示。

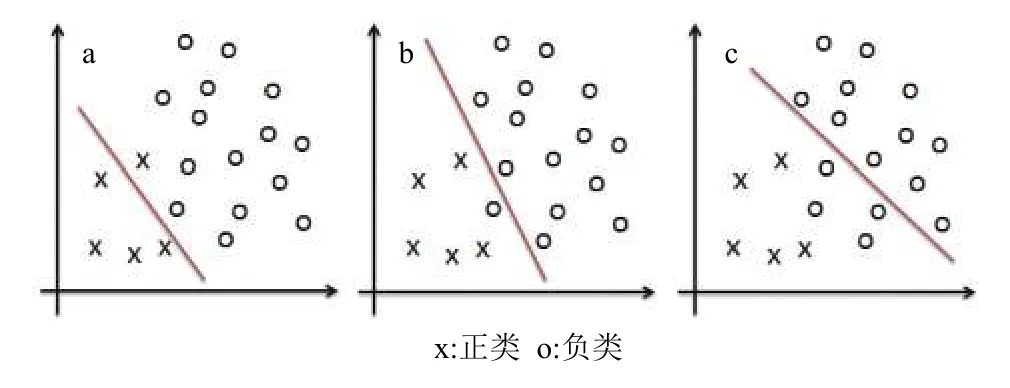
图1 不同表现的基分类器

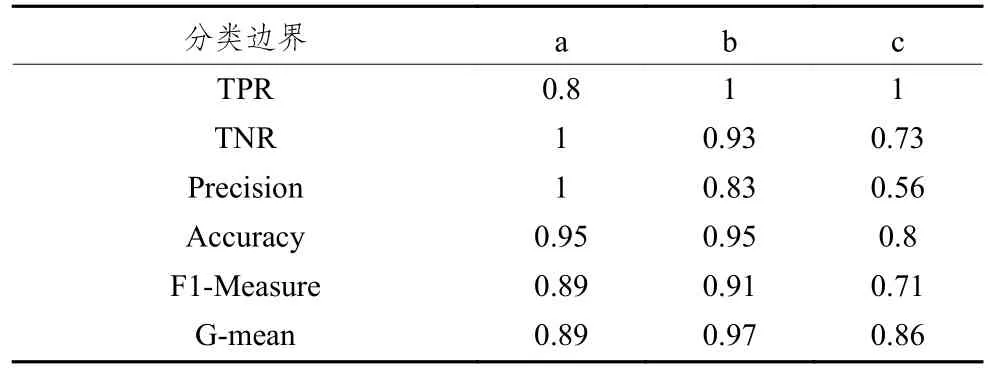
表1 各基分类器的分类表现

基分类器b和基分类器c相比于基分类器a都有着更高的TPR表现，且都在一定程度上牺牲了在Precision和TNR上的表现，但基分类器b在Accuracy上没有变差，所以从F1-Measure和G-mean上来看，整体预测表现没有变差；而基分类器c在Precision和TNR上则下降得比较多，Accuracy更差，导致了模型的整体预测表现不如基分类器a。可以推测，存在类似于b的基分类器，既有着更好TPR表现，同时整体表现也不差，如果把它们筛选再集成，就可能在不降低整体预测表现的情况下得到比集成全部基分类器更好的TPR表现。对基分类器进行选择性集成比将所有基分类器进行集成的预测效果要好，此外还能够减少集成规模，达到提高模型预测速度，降低存储需求的目的[18～19]。本文用AHP方法对SMOTEBagging模型的基分类器进行评价和选择，构建了AHP-Based Bagging模型。

（二）模型介绍

AHP-Based Bagging模型主要分三个阶段。第一阶段为基分类器训练集的生成和基分类器的训练阶段，如图2所示，先采用Bootstrap抽样的方法生成m个大小与原始训练集相同的数据集，然后用SMOTE方法生成新的少类样本，使每个数据集中的正负样本数量相同，构成m个Bag，然后利用Bag中的数据集训练m个基分类器。

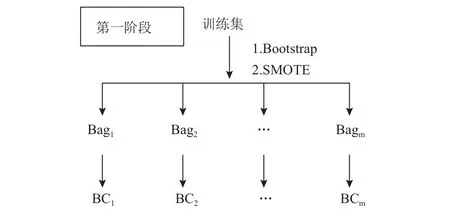
图2 AHP-Based Bagging第一阶段

第二阶段为基分类器的评价和选择阶段。为了提高SMOTEBagging在TPR上的表现，需要选择在TPR上表现好的基分类器进行集成，同时从前一小节的分析可以知道，只在TPR上表现好的基分类器并不一定有很好的整体表现，所以还需要综合考虑基分类器在其他指标上的表现，因此在第二阶段中使用AHP方法构建了一个三层的层次结构，来对基分类器进行评价和选择，如图3所示。其中，目标层为需要解决的决策问题，即对基分类器进行选择，以使选出来的基分类器集成后对少类样本有更好的预测表现，同时整体预测表现不比原来差。准则层为评价基分类器表现的4个基础评价指标。

方案层为候选的基分类器，即第一阶段得到的所有基分类器。为了实现目标层的目标，需要按照1～9的偏好程度设置各准则的权重偏好[20]。因为首要目标是选出TPR高的基分类器，所以TPR的权重偏好设置为9，同时根据上一小节的分析，Accuracy也是一个重要的指标，否则选出的基分类器的整体表现会比较差，因此Accuracy的权重偏好和TPR一样，设置为9。在样本不平衡的情况下，少类样本往往是更重要的样本，模型在TPR上的表现比在TNR上的表现要更重要，所以将TNR的权重偏好设置为1，同时，TPR也比Precision更为有用[10]，所以将Precision的权重偏好也设置为1。至此，本文确立了所有4个准则的权重偏好，得到成对比较矩阵A，如式（1）所示。计算该矩阵最大特征值对应的特征向量能够得到准则层相对于目标层的权重向量如式（2）所示。

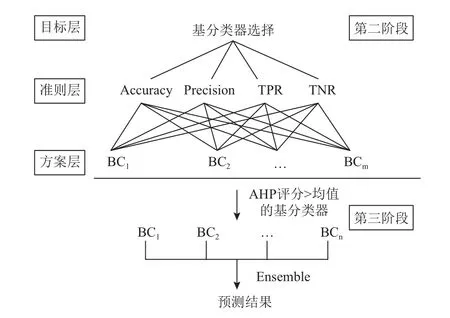
图3 AHP-Based Bagging第二、三阶段

方案层中基分类器关于准则层中某个指标的成对比较矩阵则通过基分类器在out-of-bag数据集上的验证结果两两比较构成，计算每个成对比较矩阵最大特征值所对应的特征向量，得到方案层中各基分类器关于该评价指标的权重向量如式（3）所示，其中m为基分类器的个数。最后计算基分类器关于决策问题的权重向量也就是基分类器的AHP评分，如式（4）、式（5）所示。

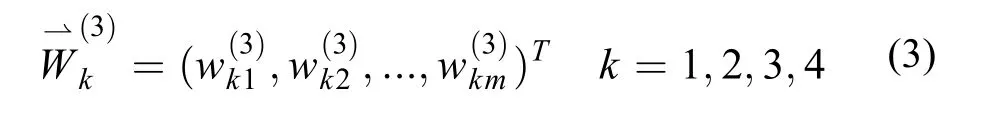
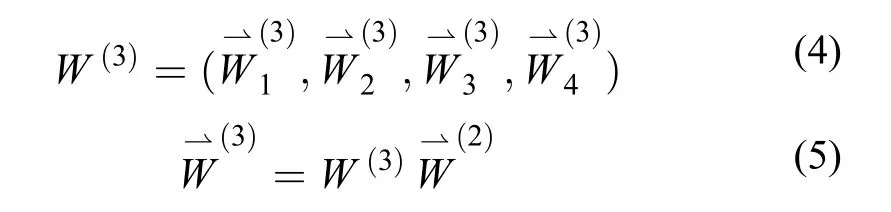
第三阶段是基分类器的集成阶段。选择在第二阶段中AHP评分高于平均值的基分类器来得到最终的预测结果。Bagging中的集成方法有很多种，在分类问题中一般是用多数投票的方法。与多数投票的集成方法相比，按概率集成能更好地保留基分类器输出的概率信息[21]，因此AHP-Based Bagging模型按式（6）、式（7）对选出的基分类器的预测结果进行集成。

三、实验

（一）实验数据

为了验证AHP-Based Bagging模型是否能达到改进目的，本文在27个来自不同领域的数据集上进行了实验。这些数据的基本信息如表2所示，其中软件缺陷预测相关的数据集来源于NASA的MDP库，其他的数据集都是来源于UCI的公开数据集。且这些数据集都存在一定程度的样本不平衡问题，不平衡率（IR）最小到1.25，最大到31.98。

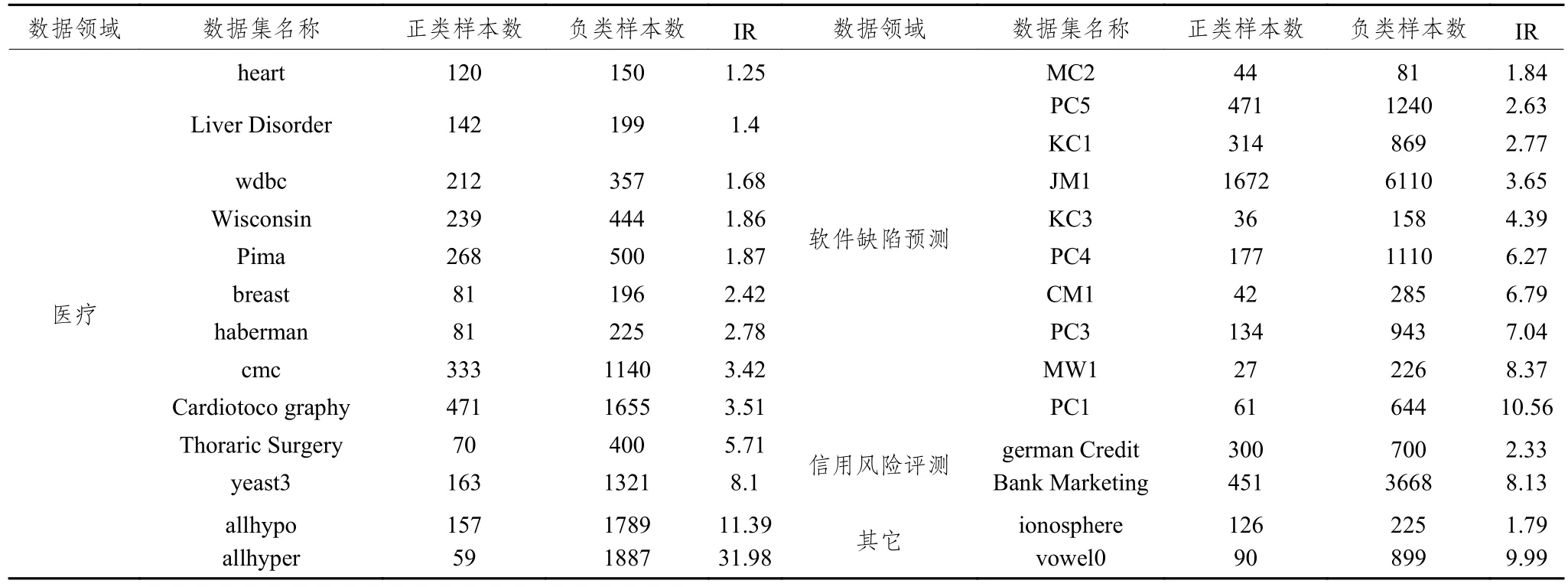
表2 AHP-Based Bagging实验数据集

（二）实验设置

实验将在BP神经网络（BPNN）、Logistic回归模型（LR）和支持向量机模型（SVM）3种不同的基分类器设置以及不同的Bag数设置下获取AHPBased Bagging和SMOTEBagging的TPR，并通过F1-Measure、G-mean和AUC这三个指标来考察模型的整体预测表现[6]。其中，Bag数两种Bagging模型都通过R语言实现，基分类器通过调用RWeka包中的相关函数实现，BPNN采用3层的神经网络，输入层节点数量与数据集属性数相同，由于是二分类问题，所以输出层节点数为1，隐藏层的节点数量采用RWeka中的默认设置，为属性数与类别数和的一半，SVM模型由RWeka中的SMO函数实现，采用线性核函数。

（三）实验结果及分析

通过对AHP-Based Bagging和SMOTEBagging在27个数据集下10折交叉检验的结果进行平均，本文得到了模型在TPR、F1-Measure、G-mean、AUC四个指标上的平均表现以及模型的平均集成规模，如图4所示。图例中AHPB表示AHP-Based Bagging，SMTB表示SMOTEBagging，AHPB.BPNN表示以BPNN为基分类器的AHP-Based Bagging模型，其他模型名称含义类似。

从图中可以看出，无论是以BPNN、LR还是SVM作为基分类器，AHP-Based Bagging在TPR上的表现都要优于SMOTEBagging，尤其是在以BPNN作为基分类器时表现出了较大的优势；在F1-Measure和G-mean上，AHP-Based Bagging能有和SMOTEBagging基本一致甚至更好的表现；在AUC上，仅在以SVM作为基分类器时，AHP-Based Bagging的值要比SMOTEBagging低，而且随着Bag数的增多差距也在减小。

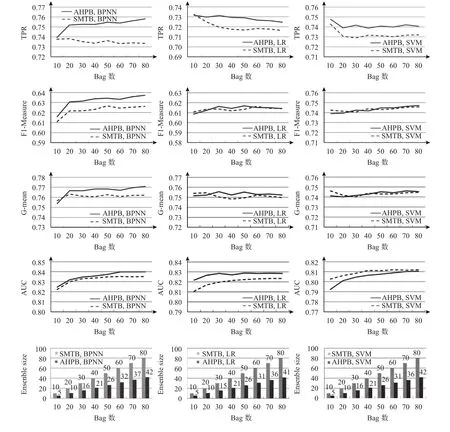
图4 AHP-Based Bagging与SMOTEBagging对比实验结果

表3是在0.05的置信度上对AHP-Based Bagging模型和SMOTEBagging模型在各指标上的表现差异进行成对T检验的结果。表中“↑”和“↓”分别表示AHP-Based Bagging的表现相比于SMOTEBagging的表现有显著的提高和下降，“—”表示二者的表现没有显著差异。

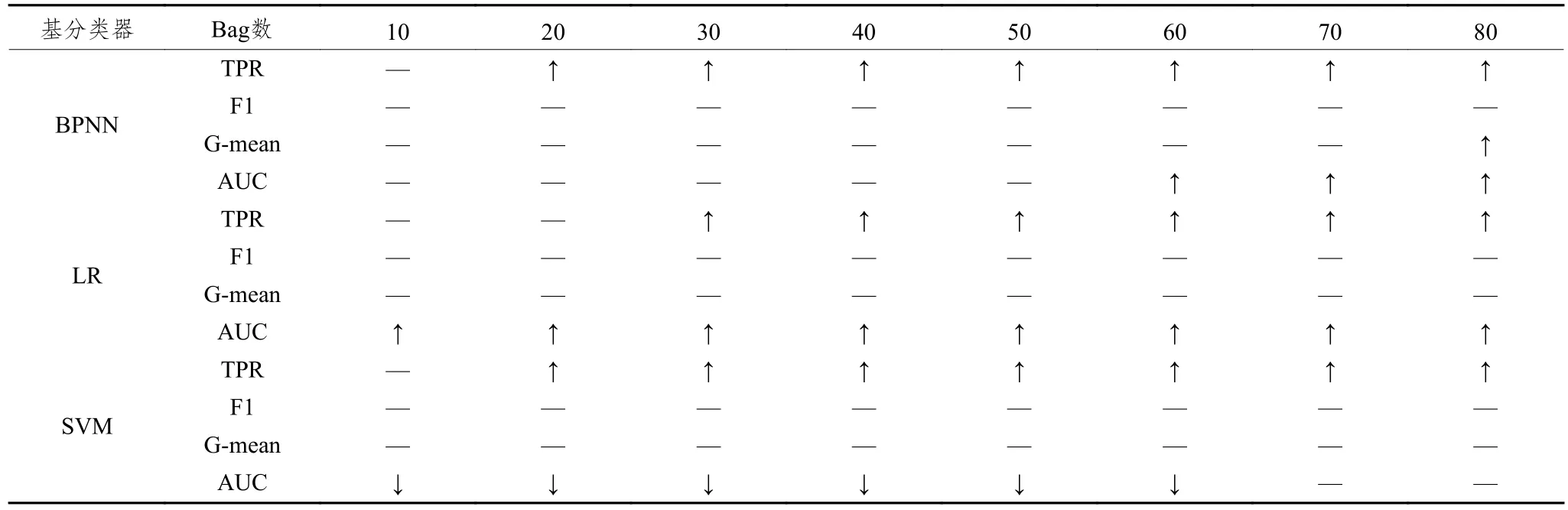
表3 AHP-Based Bagging与SMOTEBagging的成对T检验结果

从表中可以发现，在TPR上，只在Bag数较少时存在差异不显著的情况，随着Bag数的增多，AHPBased Bagging在TPR上的表现都是显著优于SMOTE Bagging的。在F1-Measure和G-mean上，两种Bagging模型的表现是无显著差异的。而在AUC的表现上，两种Bagging模型的差异会由于基分类器类型的不同而不同，以BPNN作为基分类器时，一开始AHP-Based Bagging的优势并不明显，随着Bag数的增多，从Bag数为60以后，AHP-Based Bagging的表现开始显著优于SMOTEBagging的表现；在以LR作为基分类器时，AHP-Based Bagging的表现从一开始就要显著优于SMOTEBagging；而以SVM作为基分类器时，AHP-Based Bagging的AUC表现都要显著差于SMOTEBagging，直到Bag数为70以后，差异才变得不显著。

通过以上分析可以知道，AHP-Based Bagging能比SMOTEBagging有更好的TPR表现，同时整体表现也不会变差，甚至能有所提高，但提升效果会受两个因素的影响。一是Bag数，Bag数越多，训练的基分类器越多，AHP-Based Bagging越容易比SMOTEBagging表现好；二是用于作为基分类器的分类模型的稳定性，分类模型越不稳定，提升效果越好，在以BPNN和LR作为基分类器时，能在显著提高TPR表现的同时维持模型在F1-Measure、G-mean和AUC上的表现，而在以SVM作为基分类器时，只有训练更多的基分类器，AHP-Based Bagging才能在不显著降低AUC表现的情况下有比SMOTEBagging更好的TPR表现。这两个因素能影响提升效果的原因在于它们直接影响着Bagging模型中基分类器的多样性，Bag数越多或是作为基分类器的分类模型越不稳定，得到的基分类器的表现越多样化，从中选出符合要求的基分类器的可能性就越大，AHP-Based Bagging相比于SMOTEBagging的提升效果也就越好。

AHP-Based Bagging不仅有更好的TPR表现，还有着更小的集成规模（Ensemble Size）。集成规模指的是训练好的Bagging模型中所包含的基分类器的数量。图4中最后一行是在不同Bag数设置下AHP-Based Bagging和SMOTEBagging模型的集成规模对比。可以发现SMOTEBagging由于是对所有的基分类器进行集成，所以最终训练完成的模型中所包含的基分类器的数量与Bag数是一致的，而AHP-Based Bagging通过对基分类器进行选择性集成，在同样的Bag数下，训练完成后的集成规模明显比SMOTEBagging模型的集成规模要小，经过计算，以BPNN、LR和SVM作为基分类器时，AHP-Based Bagging模型的集成规模分别只有SMOTEBagging模型的52.4%、51.3%和52.0%。更小的集成规模使得AHP-Based Bagging模型在实际应用中占用的计算资源更少，预测速度也更快。

四、结论

AHP方法在传统决策领域有着广泛的应用，本文将AHP方法引入到SMOTEBagging模型中，综合考虑多个评价指标，对基分类器进行选择性集成，构造了AHP-Based Bagging模型。通过在27个不同数据背景、不同样本不平衡率的数据集上进行实验，本文发现这样的结合不仅大幅降低了训练完成后模型的集成规模，当基分类器具有足够的多样性时，还能在不牺牲模型整体预测表现的同时，显著提高对少类样本的预测准确率（TPR），因此在少类样本更为重要的数据不平衡问题中，如信用风险预测、疾病诊断等，AHP-Based Bagging模型相比于SMOTEBagging模型具有更强的实用性和更好的预测效果。

对传统决策方法与集成学习相结合的模型研究，本文只是在前人的基础上做了有限的推进，在以后的研究中还有很多可以尝试的点，比如这种结合在基分类器类型不同的集成学习模型中是否会有更好的表现，又比如在基分类器评价的过程中考虑其他决策方法，或者研究是否有其它更合适的评价指标和阈值确定方法，以选出更合适的基分类器来实现更好的集成效果等，希望能在以后的研究工作中能做更深入的探索。