基于GSSA的双有源桥双向DC-DC变换器建模与分析

刘秀群，王润新



基于GSSA的双有源桥双向DC-DC变换器建模与分析

刘秀群，王润新

（上海海事大学物流工程学院，上海 201306）

由于双有源桥双向DC-DC变换器电感电流在一个周期内波动很大，采用传统状态空间平均法对其进行小信号建模不符合“小纹波”假设，本文采用一种常用于谐振变换器建模的广义状态空间平均法（Generalized State-Space Averaging, GSSA）来对双有源桥双向DC-DC变换器进行建模。首先介绍了基于傅里叶变换的广义状态平均法，然后根据变换器的时域状态模型，以原电路变量的傅里叶级数系数为状态变量建立广义状态平均模型，求得控制到输出的传递函数，并设计了闭环控制器。最后在MATLAB/Simulink中搭建了仿真模型，仿真结果表明，利用该模型设计的闭环控制器可使变换器输出稳定电压。

双向DC-DC变换器 广义状态空间平均 小信号建模

0 引言

双有源桥双向DC-DC变换器(Dual Active Bridge Bidirectional DC-DC Converter,以下简称DABBDC)广泛应用于电动汽车、光伏发电等具有能量双向流动的储能系统中[1]。DABDC因其高可靠性、高能量密度、高传输效率和软开关易实现等优点[2-3]，使得国内外专家学者对此做了大量分析和研究。为保证系统工作稳定，需设计良好的控制策略，而建立变换器精确的数学模型对控制器的设计具有重要意义。

在开关变换器建模方面，常用的方法有状态空间平均法、等效电路法和采样数据建模法。文献[4]采用离散建模的方法建立了DABBDC的小信号模型，设计了双闭环控制器并且在数字自动控制系统中进行了验证。状态空间平均法把开关电路等效为线性、时不变的连续电路，建模过程中忽略了纹波的影响，而DABBDC中的电感电流在一个周期内波动很大，应用状态空间平均法需对模型进行降阶处理，降低了模型的精确度[5]。Sander等人在文献[6]中提出广义状态平均法用于功率变换电路建模，与实际时域电路结果吻合良好。广义状态平均法的基本思想是利用傅立叶级数将一个时变的状态方程转换为线性时不变的状态方程，用低阶谐波分量来近似原始信号，然后将傅里叶级数系数作为状态变量建立系统的状态空间模型[7-8]。本文将采用广义状态平均法对双有源桥双向DC-DC变换器进行建模。

1 广义状态空间平均法

广义状态空间平均建模方法要用到关于傅里叶级数系数的两个重要性质，即傅里叶系数微分特性和傅里叶系数频域卷积特性。

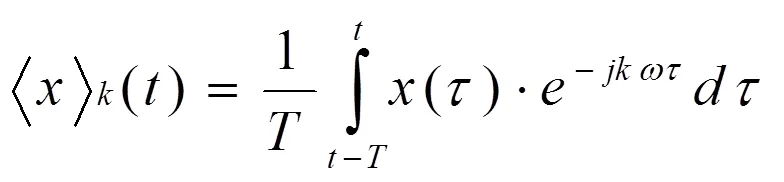
由上式（2）可知，如果用R和I来表示复数的实部和虚部，则有

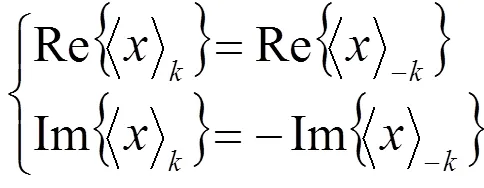
通过傅立叶系数表达式（1），可以得到它的微分形式

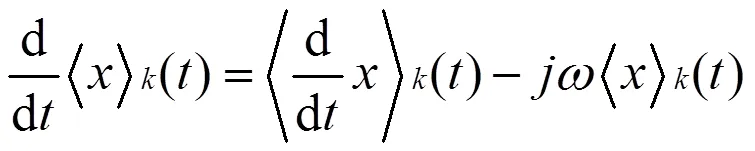
原始信号用傅里叶系数表示的表达式如下：

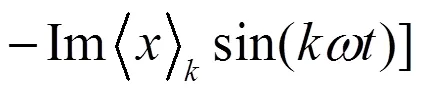
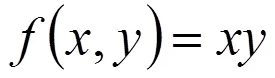
双有源桥双向DC-DC变换器工作在稳定状态时，变压器电感电流i呈现出良好的正弦特性，其零次谐波分量近似为零，于是可以用基波分量来近似代替。而输出电压等直流分量则采用零次谐波分量来代替其稳态和暂态特性。根据系统的时域非线性方程组，便可得到广义状态空间平均模型。

2 双有源桥双向DC-DC变换器的建模

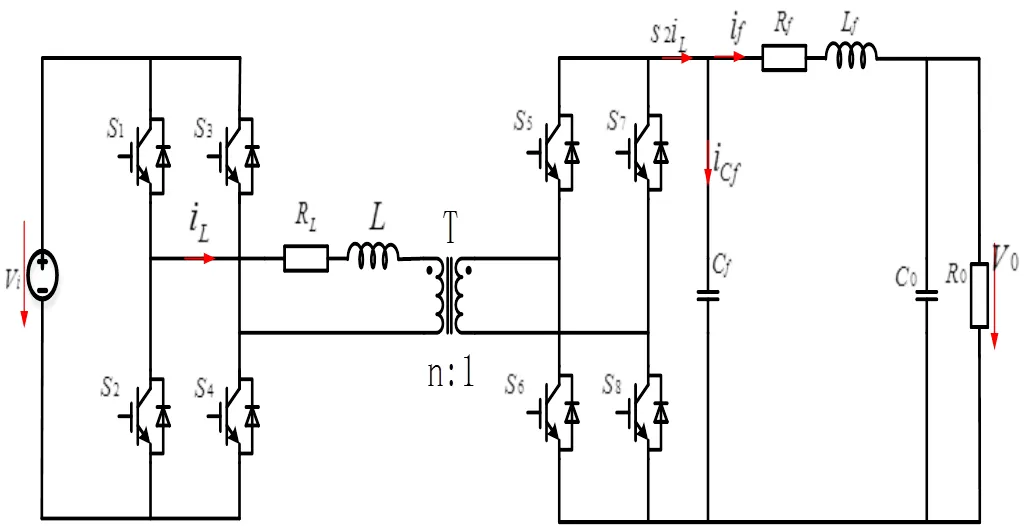
图1 双向全桥DC-DC变换器

根据移相控制原理，左边H桥的开关模式用1()表示，右边H桥的开关模式用2()表示。在忽略变压器漏感电流和开关器件压降，并且开关为理想器件的条件时，隔离变压器两端电压v、v及流过电感的电流i()的波形如图2。

单移相控制下变换器的传输功率为

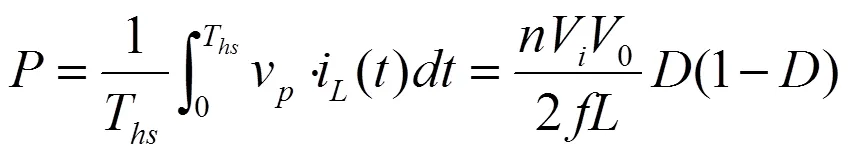
当=0.5时，变换器传输功率取得最大值：

图2 变换器工作波形

由于开关管的开关过程时间较短，为了便于分析，假定开关过程瞬间完成。选定输出电压0，变压器电感电流i，滤波器电容电压v，滤波器电感电流i为状态变量，得到一个开关周期内的电路状态方程为：

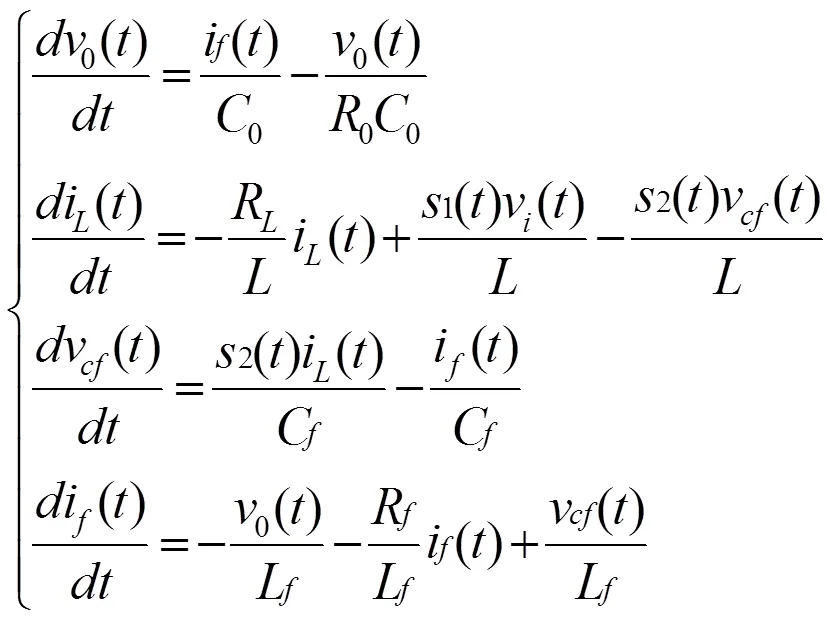
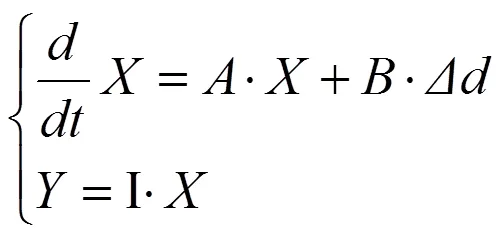
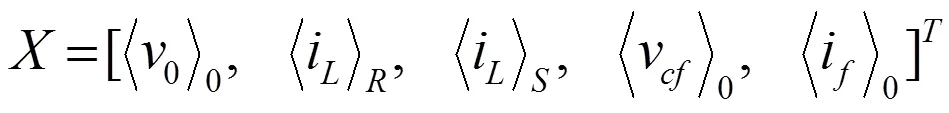
3 变换器闭环控制设计

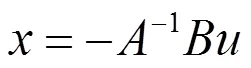
在只考虑电感电流直流分量和一次谐波分量的情况下，电感电流稳态值可以近似表示为

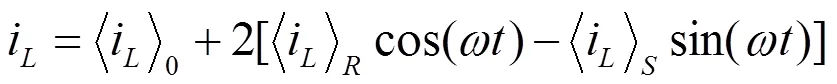
根据以上广义状态空间模型，可以求出系统控制到输出的开环传递函数为

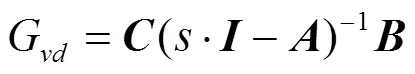
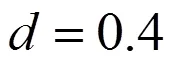
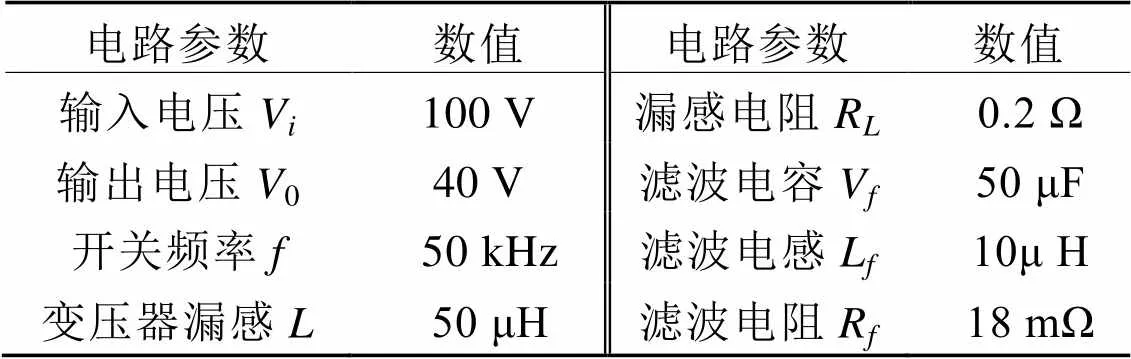
表1 双有源桥双向DC-DC变换器参数

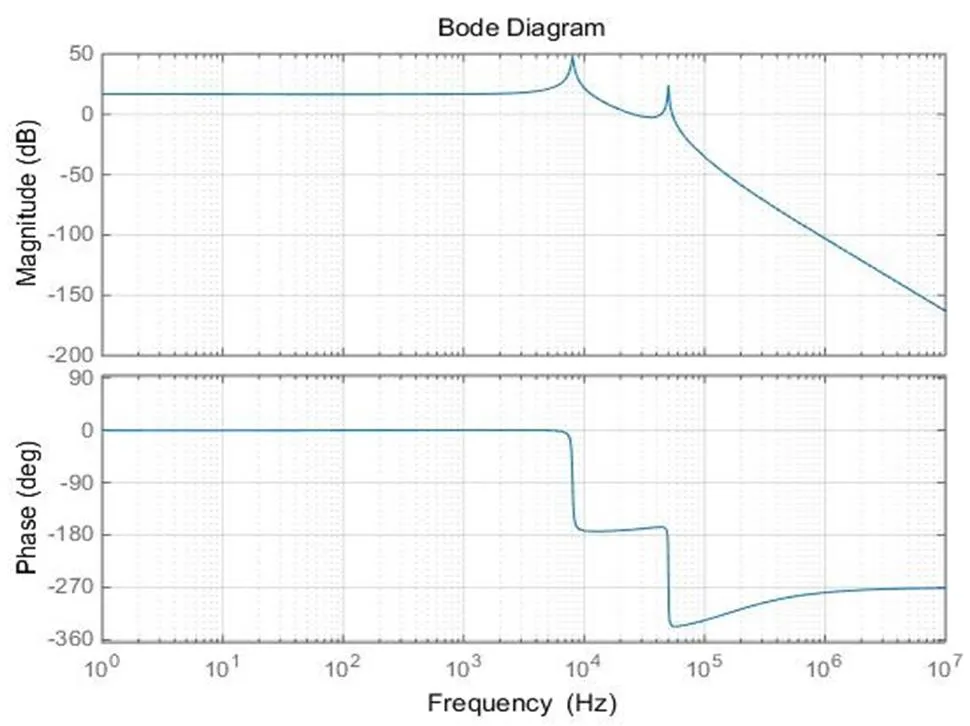
图3 控制-输出传递函数伯德图

从系统伯德图可以看出系统开环低频增益较低，在穿越频率处，相角裕度很小，系统稳定性较差。为了获得更好的动态性能和减小系统的稳态误差，本文设计了电压单闭环控制系统，如下图4所示。

图4 变换器闭环控制框图

利用MATLAB中的SISOTOOL工具进行了PI调节器的参数整定，求得调节器参数为K=4.5，K=0.26。

4 仿真验证结果与分析

基于MATLAB/Simulink对设计的闭环控制策略进行验证，通过控制保持副边侧输出电压恒定为40 V。仿真波形如图5所示，可见变换器输出电压稳定，系统响应速度快，满足控制器设计要求。

图5 稳态输出电压

5 结论

本文基于广义状态空间平均法对双有源桥双向DC-DC变换器建立了小信号模型，并设计了闭环控制策略，Matlab/Simulink仿真结果表明该模型具有较高的精确度。

[1] 王博洋, 魏立彬, 张宇, 等. 基于双向全桥DC-DC变换器增广状态控制系统研究[J]. 电气传动, 2017, 47(11): 25-30.

[2] DeDoncker R W, Kheraluwala M H, Divan D M. Power conversion apparatus for DC/DC conversion using dual active bridges[P]. U.S.: Patent 5, 027, 264. 1991-6-25.

[3] 武琳, 刘志刚, 洪祥. 隔离式双向全桥DC-DC变换器的功率控制特性比较与分析[J]. 电工技术学报, 2013, 28(10): 179-187.

[4] Krismer F, Kolar J W. Accurate small-signal model for the digital control of an automotive bidirectional dual active bridge [J]. IEEE Transacion on Power Electronics, 2009, 24(12): 2756-2768.

[5] 蒋小平, 魏立彬, 彭朝阳, 等. 基于广义状态平均法的双有源全桥变换器建模[J]. 电子技术应用, 2015, 41(7): 132-135, 139.

[6] Sander Seth R, Noworolski J Mark , et al. Generalized averaging method for power conversion circuits[J]. IEEE Transacrions on Power Electronics, 1991, 6(2): 251-259.

[7] 周继昆, 吴付岗, 张荣. LCL型IPT系统广义状态空间平均法建模与分析[J]. 科技通报, 2015(11): 215-219.

[8] 游江, 康少波, 罗耀华. 广义状态空间平均法用于PWM整流器的建模[J]. 电测与仪表, 2009, 46(8): 67-70.

Modeling and Control of Dual-active-bridge Converter Based on GSSA

Liu Xiuqun, Wang Runxin

(School of Logistics Engineering, Shanghai Maritime University, Shanghai 201306, China)

TM46

A

1003-4862（2018）08-0056-04

2018-04-10

刘秀群（1994-），男，硕士研究生。专业方向：电力电子系统建模与控制。E-mail: lxqahu@163.com