基本的周期性脉动负载供电特性分析

林 松，孙 勇



基本的周期性脉动负载供电特性分析

林 松，孙 勇

（南京电子技术研究所，南京 210039）

针对基本的周期性脉动负载供电电路，采用分段平均方法，分析了串联式、并联式和混合式供电电路的特性。提出了脉动负载的等效电阻的概念，基于等效电阻，含脉动负载的非线性电路在满足一定条件下可以等效为一般的线性电路形式，并且针对三种基本电路形式，推导了周期平均电流和功率的计算公式，最后通过电路实验和仿真分析，对计算方法进行了验证。

周期性脉动负载 等效电阻 分段平均方法 周期平均输入电流

0 引言

随着电子设备的发展，用电负荷特性各异，传统的负荷可以用阻性负荷、容性负荷、感性负荷或者混合负荷表示，由此类负荷与电源构成的供电电路可以采用常规的方法进行分析和设计。目前电子设备多为直流电源供电，并且部分负载电流周期性变化，引起供电电路的稳定性下降，供电性能受到影响，对于雷达发射单元等这类周期性脉动负载，除了采用计算机仿真分析方法，目前还没有有效的理论分析方法。通过大量仿真分析，可以在一定程度上优化供电电路参数，得到较好的设计方案[1]，但是由于不能得到电路参数与设计指标之间的解析关系，缺乏对供电性能的深入理解，难以得到最优的设计方案。

2015年以来解放军理工大学和南京电子技术研究所对含有脉动负载的供电系统开展了试验研究[2-3]，结果表明，脉动负载对供电系统有重要影响，并且脉动负载的周期和占空比是主要影响参数。2018年，中国船舶及海洋研究工程设计研究院分析了雷达脉冲性负荷对柴油发电机组特性的影响，得到了调速器介入前后，转速跌落、恢复规律和稳态过程转速的变化率[4]。由此可见，雷达的脉冲性负载特性对船舶供电系统产生了重要的稳定性影响，并且逐渐得到广大学者的重视，本文从雷达脉冲性负载的本质特性出发，研究基本的周期性脉动负载供电特性。

对于开关电源电路建模分析，最常用的方法是状态空间平均法，有些学者采用状态空间平均的方法对DC/DC变换器的行为级建模进行了研究[5,6]，但是该方法主要应用于开关变换器本身的建模和环路特性分析，未涉及脉动负载对供电的影响。因此，有必要针对基本的周期性脉动负载供电电路的特性开展理论研究，本文通过对三种最基本的周期性脉动负载供电电路进行研究，提出一种有效的理论分析方法，用来指导供电电路的设计，具有理论和工程应用价值。

含周期性脉动负载的供电电路由于含有开关器件和非线性器件，使得整个供电电路成为强非线性时变系统，传统的线性电路分析方法不再适用。本文基于分段平均的思想[5]，提出一种有效的分析方法，考虑含有开关器件的周期性脉动负载工作特性，采用分段平均方法进行分析，推导出电压、电流和功率的解析关系。

1 周期性脉动负载基本电路

根据周期性脉动负载相对供电端口的用电特性，将含周期性脉动负载的供电电路分为三种类型：串联式、并联式和混合式，由于串联式电路是构成其他电路形式的基础，因此先对周期性脉动负载基本电路——串联式电路进行研究分析。

1.1 周期性脉动负载基本电路

周期性脉动负载的基本电路如下图所示，负载支路按照某一周期和固定占空比导通和断开。

图1 周期性脉动负载基本电路

上图中开关S的通断由PWM信号控制，该PWM信号周期为、占空比为（0＜＜1），其开关S的状态由如下函数确定：

当PWM信号输出1时，开关S导通；当PWM信号输出0时，开关S断开。

假设输入电压波形如图2所示。由于电源的非理想特性及周期性脉动负载对电源的扰动，输入电压u()表现为周期函数，周期为，电压最小值为min，最大值为max。在[0,]期间，开关S闭合，有负载电流；在[,]期间，开关S断开，无负载电流。因此，可以计算周期平均输入电流：

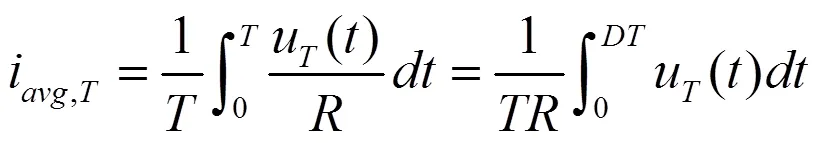
1.2 电压特性

[0,]阶段的平均输入电压：

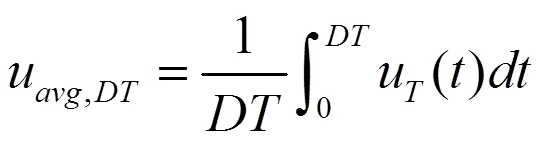
[,]阶段的平均输入电压：

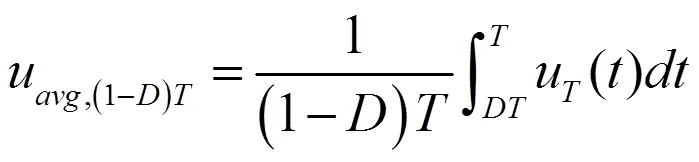
周期平均输入电压：

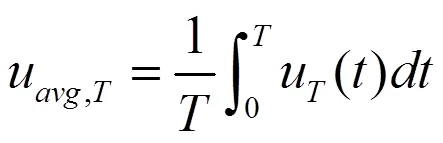
根据上述定义，在脉动负载电路（见图1）中，平均输入电压：

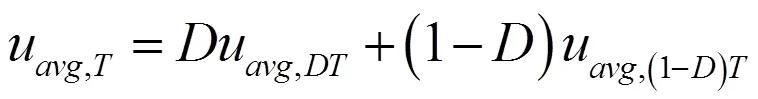
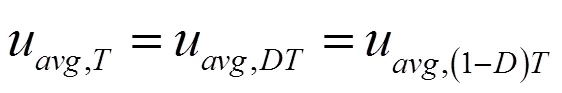
1.3 电流特性与等效电阻

在[0,]期间，开关S闭合，有电流产生，可以计算[0,]阶段的平均输入电流：

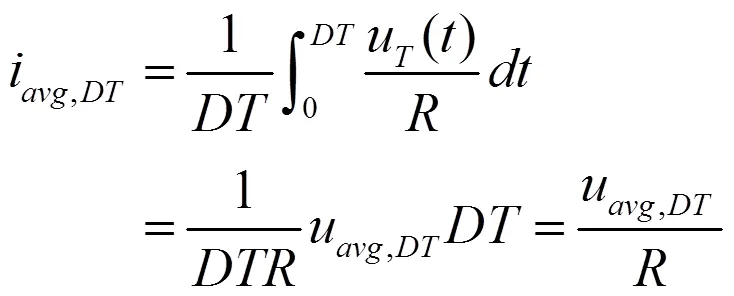
根据式（2）、（3）、（8），周期平均输入电流i与[0,]阶段的平均输入电流i有如下关系：

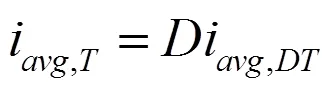
根据式（9），可得：

¢为该电路的等效电阻，图1的等效电路即为在¢两端施加等效输入电压u。

1.4 功率特性

图1基本电路的周期平均输入功率：

令

1.5 一类特殊情形

当u=u(1-D)T时，等效输入电压u可以替换为u。下面针对这类特殊情形进行分析：

当输入电压u()为三角波时，如下图所示：

由式（3）-（6），可以得到三种平均输入电压有如下关系：

由式（8），可以计算[0,]阶段的平均输入电流：

由式（10），可以计算周期平均输入电流：

2 周期性脉动负载并联式电路

周期性脉动负载的并联式电路如图4所示。

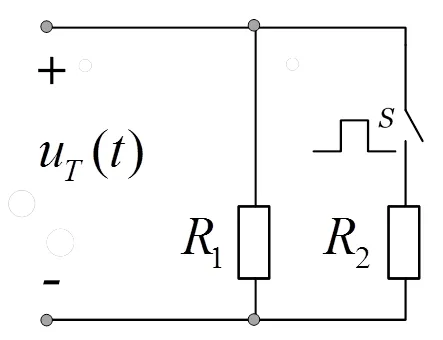
图4 周期性脉动负载并联式电路

该并联式电路中的周期平均输入电流为：

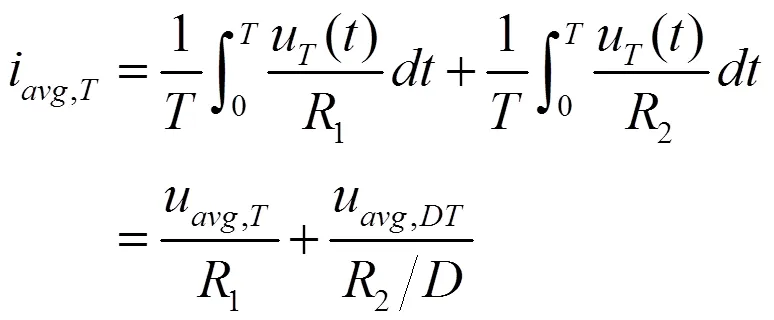
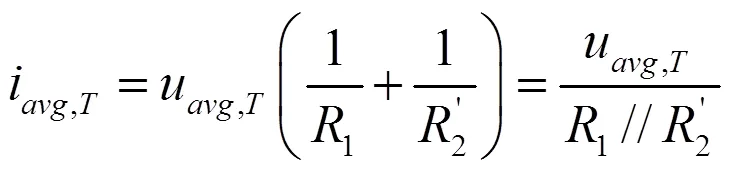
该并联式电路的周期平均输入功率为：

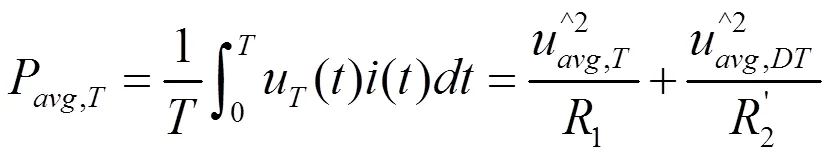
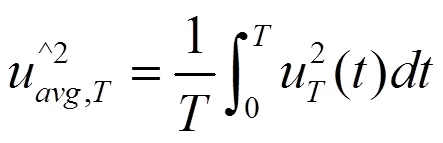
由式（21）可知，并联式电路的周期平均输入功率等于常规负载支路和脉动负载支路的周期平均输入功率之和，并且脉动负载支路的周期平均输入功率与周期性脉动负载基本电路的功率计算方法一致，因此，当有多个脉动负载支路并联时，也可以按照该方法计算。

3 周期性脉动负载混合式阻性电路

周期性脉动负载混合式电路包含多种形式，下面分析最常见的基本阻性电路，如图5所示。

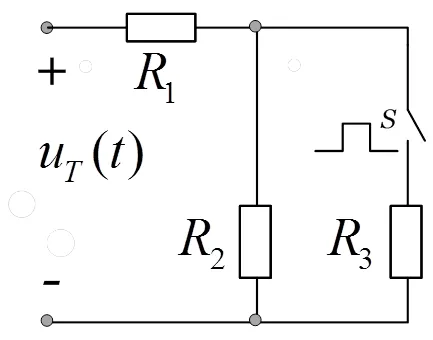
图5 周期性脉动负载混合式阻性电路

该混合式电路中的周期平均输入电流为：

当满足u=u=u(1-D)T时，可得：

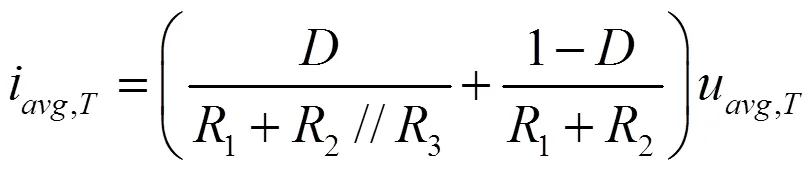
此时，该电路的等效电阻为：

根据图5，该混合式电路中的周期平均输入功率为：

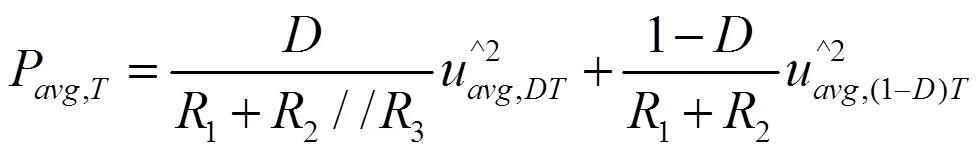
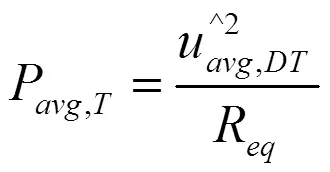
4 仿真及实验验证

由于周期性脉动负载的串联式和并联式电路是混合式阻性电路的特殊形式，下面对混合式阻性电路（见图5）进行仿真及实验验证。选择典型的周期性输入电压：

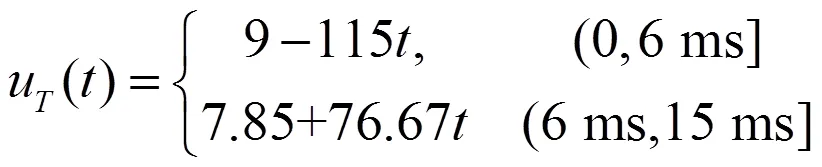
假定电路中电阻分别为：1=0.143 Ω；2=6.6 Ω；3=0.59 Ω；开关S的周期=15 ms，占空比=0.4；周期性输入电压的周期=15 ms。

根据式（15），可以计算得到上述三种平均脉动电压有如下关系：

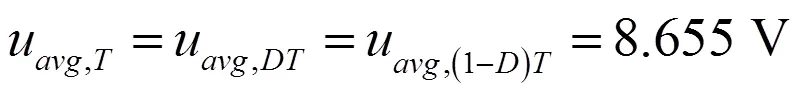
将1、2、3、和代人式（26），可以得到等效电阻：

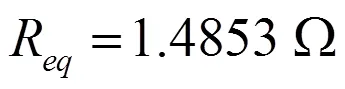
则周期平均输入电流分别为

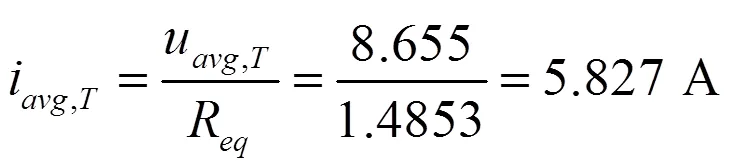
用Saber软件对图5电路进行仿真分析，得到输入电压和电流波形如图6所示。

由图6可知，周期平均输入电流为5.8272 A，与理论计算结果一致。

为了进一步进行验证，对图5电路进行实验测试，电路中u()用一台输出并联70000mF电容并具备限流功能的直流稳压电源来实现，含3的脉动负载支路用直流电子负载的恒流动态加载功能实现。测试结果如图7所示。

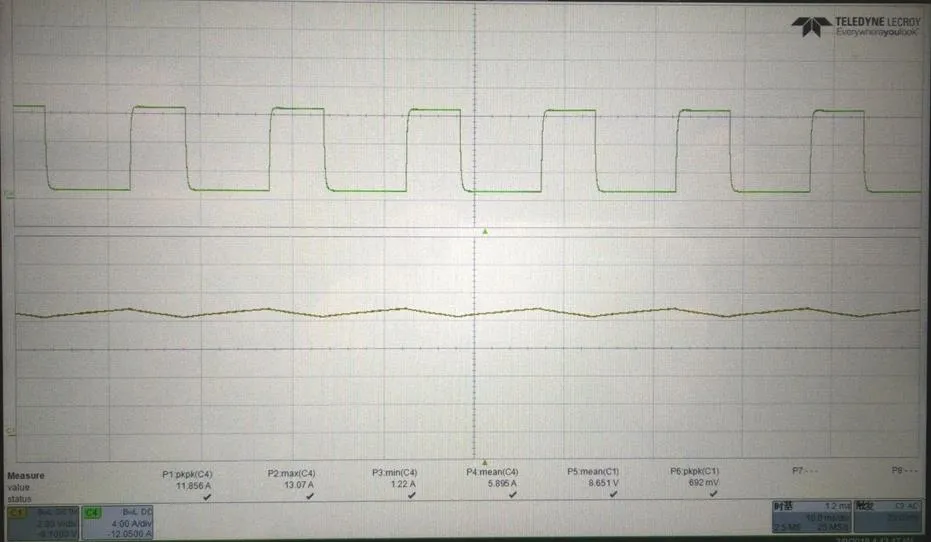
图7 实测的周期性输入电流和电压波形

将计算、仿真和实验结果对比，如下表所示：

表1 计算、仿真与实验结果对比

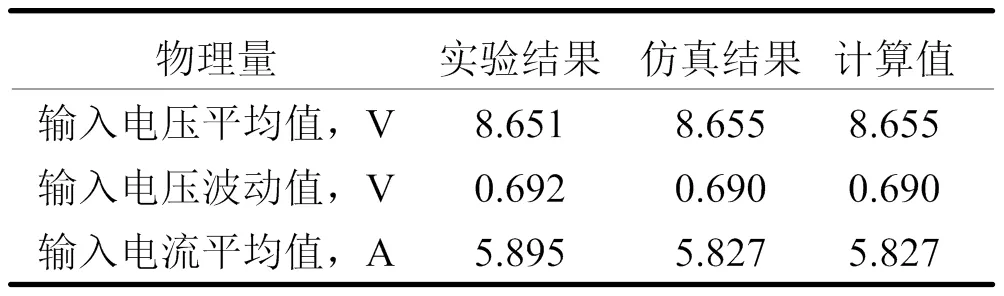
由上表可知，仿真结果与理论计算结果一致，实验结果与理论分析值也基本一致，输入电流平均值有些误差，主要是脉动负载支路用直流电子负载的恒流动态加载功能替代所致。

根据式（13）可以计算得到一个周期中两阶段的平均输入电压平方为：

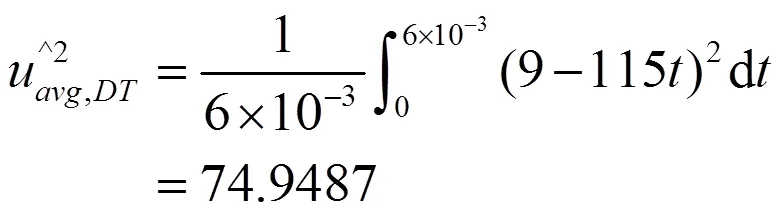
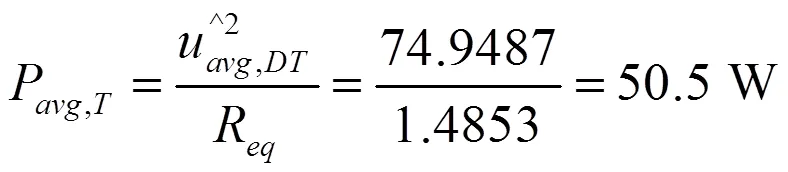
通过仿真，周期平均输入功率仿真结果为50.5 W，与理论计算值一致。通过上述关于周期平均输入电压、电流和功率的实测、仿真和计算结果的对比，三者基本一致，验证了本文关于周期性脉动负载供电特性分析的正确性。

5 结论

本文针对基本的周期性脉动负载供电电路进行研究，从简单到复杂，依次分析了串联式、并联式和混合式阻性电路的特性，通过采用分段平均的方法，提出了脉动负载的等效电阻概念，基于等效电阻，原来的非线性电路在满足一定条件下可以等效为常规的线性电路形式，并且针对三种基本电路形式，推导了周期平均电流和功率的计算公式，最后通过电路实验和仿真分析进行了验证。

本文提出了基本的周期性脉动负载供电电路的分析方法，文中推导的关于等效电阻、周期平均电流和功率的计算方法构成了周期性脉动负载供电电路的分析基础，可用于雷达发射单元供电设计分析，该方法也为以后分析复杂的周期性脉动负载供电电路提供了理论依据和借鉴方法，具有一定的理论应用价值。

[1] 胡亚超, 徐晔, 李建科, 等. 柴油发电机组－脉冲负载系统运行行为仿真[J]. 现代雷达, 2015, 37(6):74-77.

[2] 陈静静, 李建科, 徐晔, 等. 柴油发电机组带非线性负载的实验研究[J]. 现代雷达, 2015, 37(5):84-87.

[3] 李锴, 李建科, 季少卫, 等. 一种现代雷达非线性脉冲特性的模拟装置[J]. 现代雷达, 2016. 38(3): 91-94.

[4] 吴骏, 庞宇, 赵凡琪. 脉冲负荷柴油发电机组特性研究[J]. 船电技术. 2018, 38(2): 50-56.

[5] Hong S S, Byungcho C. Technique for developing averaged duty ratio model for DC/DC converters employing constant on-time control[J]. Electronics Letters, 2000, 36 (5): 397-399.

[6] Ali Davoudi, Juri Jatskevich. Realization of parasitics in state-space average-value modeling of PWM DC-DC converters[J]. IEEE Transaction on Power Electronics, 2006, 21(4), 1142-1147.

Power Circuit Characteristic Analysis with Basic Period Pulse Load

Lin Song, Sun Yong

( Nanjing Research Institute of Electronics Technology, Nanjing 210039, China )

TN701

A

1003-4862（2018）08-0017-05

2018-04-09

林松（1970-），男，高级工程师。研究方向：雷达电源系统。E-mail: linsong001@163.com