经纬仪与激光测距仪组合系统的误差分析及标定方法

罗明成，王铜，董岚，罗涛，梁静，李波，柯志勇，何振强，马娜

(1.中国科学院高能物理研究所，北京 100049；2.东莞中子科学中心，广东 东莞 523803)

0 引言

激光跟踪仪具有测量效率高、测距精度高等优点，目前工业中大尺寸高精度的三维测量通常采用激光跟踪仪系统[1-6]。Leica AT403激光跟踪仪绝对测距误差为±10 μm，测角误差为±15 μm+6 μm/m，其坐标测量误差主要受测角误差影响，而测角误差与测量距离有关，随着距离增大，激光跟踪仪对靶球中心自动识别探测的精度降低。因此，随着测量距离增加，激光跟踪仪系统点位相对误差也随之增大[7-9]。此外，激光跟踪仪测量对环境要求高，恶劣环境下其有效测量距离进一步减小，再加上系统价格昂贵，限制了激光跟踪仪的大规模应用。在国家大科学装置中国散裂中子源的二级隧道网测量过程中，为了加强网形结构和提高网点精度，需要对控制网进行大跨度的高精度测角和测距，因此，本文提出将经纬仪高精度测角以及激光测距仪高精度测距优势结合起来，形成一套大尺寸高精度的测量系统。在全站仪推出前，一些经纬仪为了实现测距，将激光测距仪安装在经纬仪立柱顶部，这种组合式经纬仪为了将测距仪测量的距离转换为经纬仪中心到目标的距离，测量反射目标均是采用上下竖置的圆棱镜，两个圆棱镜的距离等于测距仪到经纬仪仪器中心的距离，因此，测距仪对上面圆棱镜的测量距离就等于经纬仪仪器中心到下面圆棱镜的测量距离。但是这种测量方式要求测点周围空间大、上下靶标严格竖置，导致测量很不方便。因此，本文提出一种新的方法来实现经纬仪的高精度测距。

1 经纬仪与激光测距仪组合系统

通过一个可精密调整的球形座工装，将激光测距仪固定在经纬仪的立柱上，装配成经纬仪与激光测距仪组合测量系统。测距时，将激光测距仪对准靶球目标，测得测距仪至靶球目标的距离，同时将经纬仪也瞄准靶球目标，测得经纬仪至靶球目标的天顶距，最终通过计算即可得到经纬仪至靶球目标的距离，完成大尺寸高精度的测量任务。

1.1 经纬仪介绍

h3,选用Leica研发的TM6100A电子经纬仪，其具有如下优势：①采用新型直接驱动技术，抗干扰能力强、稳定性高、可靠性好；②具有新型操作面板，简化了使用流程，易操作且测量效率高；③具有新型微调把手，使得困难位置的测量更加容易，且由于这一新技术结构中没有齿轮，运行噪声比传统经纬仪小；④采用新型电池设计理念，维护成本低且能耗少；⑤测量精度高，其一测回水平方向和竖直角标称测量误差为±0.5″。

1.2 激光测距仪介绍

目前市面上的独立式绝对测量仪为Leica的μ-base激光测距仪，它采用绝对测距技术，基于相位法测距原理，通过测距频率和带宽提高测距精度，全量程测距误差为±10 μm[10-11]。

μ-base激光测距仪主要由主机、球形精密机械连接装置、通信接口盒、电源适配器以及软件组成，如图1所示。

图1 μ-base激光测距仪

μ-base激光测距仪主机下部设计为球形结构，有如下好处：①球形结构的球心作为测距仪的外基准代表了测距仪的测距基点；②球形结构通过与球形安装座配合使用，实现测距仪多角度测距时，测距中心的空间位置始终保持不变。

1.3 经纬仪与激光测距仪组合系统距离测量

为了将激光测距仪加装在经纬仪上，设计一个可精密调整的球形安装座工装。将经纬仪的把手卸下，通过螺丝将工装固定安装在经纬仪的立柱上。测量时，将激光测距仪安装在球形安装座上，激光测距仪瞄准靶球目标，获得测距仪至靶球目标的距离s，同时，经纬仪也瞄准靶球目标，获得经纬仪至靶球目标的天顶距θ，最终通过计算即可得到经纬仪至靶球目标的距离l。激光测距仪与经纬仪的几何位置模型如图2所示。其中，O为经纬仪的仪器中心位置，O1为测距仪的仪器中心位置，O2为测距仪仪器中心在经纬仪竖轴上的投影点，P为目标靶球的位置。OO2为测距仪到经纬仪的仪器中心距h，O1O2为测距仪偏离经纬仪竖轴的轴心偏差t，这两者可以通过机械标定的方法精确确定。O1P为测距仪测得至靶球目标的距离s，∠O2OP为经纬仪测得的天顶距θ，OP为经纬仪至靶球目标的距离l。

图2 经纬仪与激光测距仪组合系统测距方法

s2-(h-lcosθ)2=(lsinθ)2+t2-2ltsinθcosγ

(1)

那么经纬仪中心至目标的距离l为

(2)

2 组合系统测距精度分析

通过机械标定的方法，可以精确得到仪器轴心距h和测距仪偏离经纬仪竖轴的轴心偏差t。根据仪器实际外形尺寸并为了方便分析，本文取h=300 mm，t=0 mm。另外μ-base激光测距仪最佳俯仰测量范围为±25°，所以在后面分析中θ取值范围为60°～120°。

经纬仪测角误差为±0.5″，但在实际测量中要满足0.5″的最大允许误差需要进行多测回观测。因此，增大测角误差，分析当角度测量值变化1″时角度测量误差带来的测距误差。表1分析了当s一定，γ∈(0,2π)，θ在不同角度下变化1″时，l的变化量。从表1中可以看出，当θ变化1″时，经纬仪到测点的距离值l变化量最大仅为1.5 μm，远小于测距仪测距误差。故增加测角误差后，经纬仪角度测量误差引起的测距误差仍然很小，组合系统依然能够同时测得高精度的角度值与距离值。

表1 θ变化1″时 l的变化量

在对仪器轴心距h和测距仪偏离经纬仪竖轴的轴心偏差t进行精确标定时，为了指导标定过程，对h和t的标定精度进行了分析。

首先,对t的标定精度进行分析。由式(2)看出，当γ=0°时，t的变化引起l的变化最大，因此，取γ=0°，分析当s和θ一定，t变化0.01 mm时，l的变化量，如表2所示。可以看出l的变化量大致关于θ=90°对称，在θ=90°时，l变化值最大。此外，表2还可以看出l的最大变化量与t的变化量相等，为减小组合系统距离测量误差，t的标定精度应该尽可能高。测距仪测量误差为±10 μm，故轴心偏差的标定误差应不大于0.01 mm。

表2 t变化0.01 mm时l的变化量

然后,对h的标定精度进行分析。取h=300 mm，t=0 mm，此时l的值与γ无关，表3分析了在相同测量距离s和天顶距θ下，h变化0.01 mm对l值的影响。表3中可以明显看出在不同的天顶距θ值下，l的变化量为10 μm，在θ=90°时l变化量最小。测距仪测量误差为±10 μm，故仪器中心距h的标定误差应不大于0.01 mm。

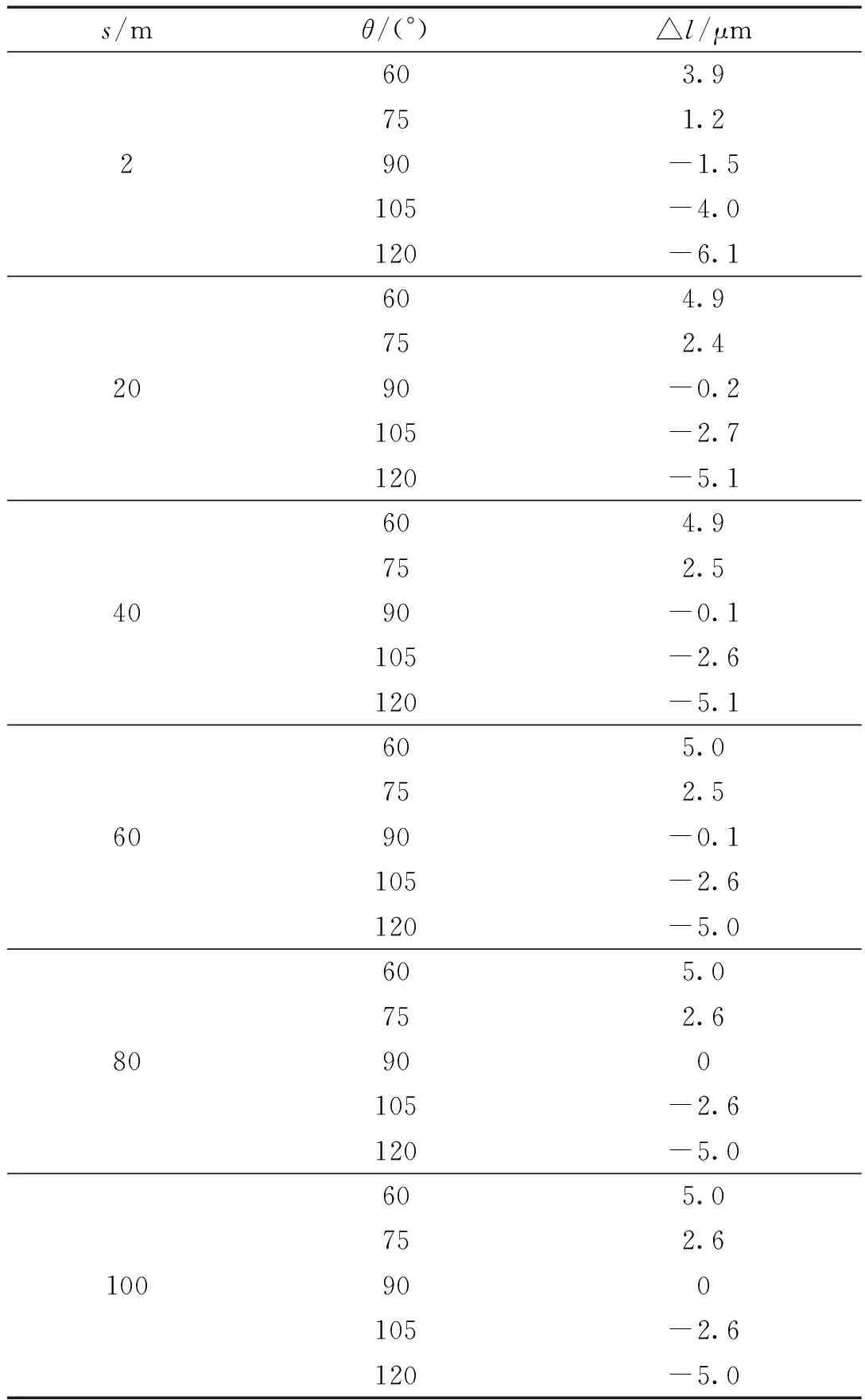
表3 h变化0.01 mm时l的变化量

结合表2与表3的数据可以发现，在大于20 m的测量范围下，h和t变化导致l的变化量受测量距离s的影响很小，但受θ的影响较大。表4列出了当s=50 m，γ=0°，在不同的天顶距θ下，当h与t均变化0.01 mm时，l的变化量。

表4可以看出，在轴心距h和偏心距t的标定误差为±0.01 mm时，标定误差引入的测距误差最大值在θ=60°时取得，为13.6 μm。考虑测距仪的测距误差，此时组合系统测距误差为±16.9 μm。

表4 h与t均变化0.01 mm时l的变化量

3 组合系统测距标定方法

结合上述精度分析，确定h和t的标定误差均为±0.01 mm。本文提出了一套具体的标定方法，可使h和t的标定误差在0.01 mm以内。

轴心偏差t的标定方法为：将经纬仪架设在三坐标机的大理石平台上并调平，在经纬仪竖直旋转轴外壳上固定一个标准锥窝基准件。旋转经纬仪，使经纬仪绕竖轴旋转，每旋转一个角度，三坐标机测头测量一次锥窝的位置，从而测量出经纬仪竖轴的位置。再将与激光测距仪球形结构等直径的圆球安置于经纬仪顶部的球形安装座上，也采用三坐标机测量出球心的位置，根据球心位置与数轴位置的偏差调整球形安装座位置，使圆球与经纬仪竖轴同轴，此时，球形安装座的调整完成。为了检验调整精度，将测距仪放置于球形安装座上，在墙上固定一个靶球目标，经纬仪水平方向360°转动，每转动一个位置，测距仪对靶球目标进行一次距离测量，采用三坐标机将测距仪调整到经纬仪竖轴上进行检验。标定所使用的三坐标机可以选用计量级三坐标机Leitz，其测量精度可以达到1 μm，故使用此方法在测距仪中心(标准球球心)处同轴度能达到5 μm，能够满足轴心偏差t的标定误差不大于0.01 mm的要求。

轴心偏差标定完成后进行仪器中心距h的标定。中心距标定方法与轴心偏差标定方法类似，将经纬仪架设在三坐标机的大理石平台上调平，在经纬仪水平旋转轴外壳上固定一个标准锥窝基准件，旋转经纬仪，使经纬仪瞄准部绕横轴旋转，每旋转一个角度，三坐标机测头测量锥窝的位置，从而测量出经纬仪横轴的位置。然后采用三坐标机对球形安装座上的圆球进行测量，得到球心的位置。最终计算出球心到横轴的距离，此标定方法也能够满足仪器中心距h的标定误差不大于0.01 mm的要求。

综合上述对轴心偏差及中心距的标定方法，最终可以得到测距仪与经纬仪组合系统的轴心偏差的误差为±0.01 mm，仪器中心距误差为±0.01 mm。

4 组合系统点位测量精度分析

三维直角坐标系下被测目标的点位坐标为

(3)

上式中l由式(2)给出，为简化分析，令t=0 mm，

γ=0 mm，h=300 mm，式(2)可简化为

(4)

则被测目标的测量误差为

(5)

其中,

(6)

(7)

(8)

(9)

故被测目标的点位误差为

(10)

令σs=0.01 mm，σh=0.01 mm，σθ=σφ=1″，分别在s为20，40，60 m时，对比组合系统与激光跟踪仪在不同天顶距下的测量点位误差，如图3所示。图中可看出在不同测量距离下θ=90°时测点误差均达到最大。

图3 系统测量点位中误差

在θ=90°时，对不同的测量系统的测量距离与点位误差进行线性拟合，拟合直线如图4所示。从图4可以看出激光跟踪仪测点中误差增长率高于组合系统，根据拟合的直线方程，可得到跟踪仪坐标测量误差为±21.7 μm+8.5 μm/m，经纬仪与激光测距仪的组合系统的坐标测量误差为±1.9 μm+6.8 μm/m。由于本文并未完全考虑仪器组合过程中的误差源，故实际测量中组合系统的测点精度会低于模拟值。但随着测量距离增加，仪器组合所产生的误差可以忽略，组合系统在长距离测量中的优势便能体现出来。

图4 测点误差随距离的拟合直线图

5 结论

本文从理论上分析了经纬仪和激光测距仪组合系统的测量误差，并未对整个组合系统进行实际测量验证。在此只介绍验证方法：将AT403激光跟踪仪当做经纬仪，将测距仪加装在激光跟踪仪上，激光测距仪和激光跟踪仪分别对目标测量获得距离，将组合系统测得的距离与跟踪仪直接测量的距离进行对比，验证本文所述标定方法的正确性以及组合系统的距离测量误差。利用经纬仪测角，激光测距仪测距，发挥仪器各自的优势，使得组合系统能够测量得到被测点高精度的角度值与距离值，理论上其测点误差接近甚至小于跟踪仪的。考虑到仪器组装误差，组合系统在短距离测量中误差会大于跟踪仪的，但是随着测量距离的增加，组装过程带来的误差可以忽略，再加上跟踪仪受环境影响较大，户外工作中有效测量距离缩短，故本系统在户外大尺寸测量中相较于激光跟踪仪有一定优势。此外该组合系统测量时需两次瞄准目标，相较于激光跟踪仪，其测量效率要低很多，适用于对测量精度要求非常高的户外大尺寸的工业测量领域。