C/SiC盖板式热防护结构动力学建模方法

孙 兵，蔡巧言，解海鸥，郭鹏飞，石 伟

（中国运载火箭技术研究院研究发展中心，北京，100076）

0 引 言

近年来，可重复使用运载器（Reusable Launch Vehicle，RLV）成为国内外研究热点，其中对热防护系统的研究是可重复使用运载技术研究中非常重要和关键的一项。RLV在工作时遭遇严峻的气动加热，热防护系统（Thermal Protection System，TPS）的材料和结构需要能够抵抗极端恶劣的气动加热情况。

第1代可重复使用运载器航天飞机使用粘接的刚性隔热瓦[1]作为其在迎风面的热防护系统，构型如图1所示。下一代低成本可重复使用运载器对热防护系统提出了质量轻、成本低、健康管理能力高、可维护性好等需求，粘接的刚性隔热瓦已不能满足这些需求。欧洲借鉴并评估了航天飞机等以往TPS方案设计的经验，提出一种采用C/SiC先进复合材料的盖板式TPS方案，构型如图2所示[2]。盖板式TPS一般安装在可重复使用运载器的迎风面以抵抗大热载，其在运输、飞行等环境中都会受到动载荷作用，对 C/SiC盖板式TPS进行模态参数预示是十分必要的。在 PRE-X项目[3]中，欧洲对C/SiC盖板式TPS的设计做了诸多研究工作，包括基于有限元模型对单块 C/SiC盖板式热防护结构装配体进行模态参数预示并开展了一系列结构动力学试验研究。

图1 航天飞机刚性隔热瓦[1]Fig.1 Rigid Insulation Ceramic of Space Shuttle

图2 盖板式热防护方案概念[2]Fig.2 Conceptual Demonstration of Shingle TPS

中国也开展了关于C/SiC盖板式TPS结构动力学方面的研究。文献[4]为分析C/SiC面板的热气弹响应，先对C/SiC面板进行了模态分析。郝秉磊、殷小玮等[5]建立了 C/SiC陶瓷复合材料螺栓连接有限元模型，并通过试验验证了模型的正确性。但是，针对 C/SiC盖板式热防护结构装配体的结构动力学研究还处在起步阶段，相关方面的文献资料有限。本文将对单块C/SiC盖板式热防护结构装配体的结构动力学建模方法开展研究，不仅可为其结构动态设计提供参考，还可为整个飞行器的模态分析、模态试验等相关工作提供支撑。

1 理论模型的建立

C/SiC盖板式TPS的固有振动特性需先建立合理的结构动力学模型，由图 2知单块盖板式热防护结构为夹层结构，建立的分析模型如图3所示，此结构模型是由两块平板和弹簧组成的二维系统。C/SiC盖板和机身蒙皮是两块弹性板，而隔热层简化为弹簧系统。因为隔热层相对较厚而模量相对较低，所以当 C/SiC盖板和机身蒙皮都有挠曲变形时，隔热层结构能被压缩。模型假设上下两块板沿长度方向的每一点都被弹簧连接。此假设是合理的，因为在实际情况下无论通过紧固件连接还是胶接，均使这3层结构的面接触在一起。

图3 单块盖板式热防护结构模型Fig.3 Structural Model of a Single Shingle TPS a，b—单块盖板式热防护结构的长和宽

不考虑外力和阻尼，利用经典的拉格朗日函数能量法推导此系统的运动方程。系统的总势能为机身蒙皮势能C/SiC盖板势能和隔热层势能的总和：

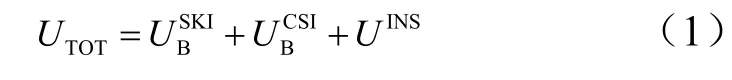
根据板的振动理论可知，假设板在振动时的挠曲变形是符合胡克定律的微小弹性变形，这种变形明显小于板厚。因此，这里只考虑了板的弯曲势能，即假设板在发生挠曲变形时，没有明显伸长。

系统的总动能 TTOT为机身蒙皮动能、C/SiC盖板动能和隔热层动能的总和：

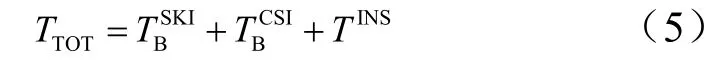
式中

将式（1）～（9）代入式（11）中得到无阻尼系统自由振动运动方程：

将式（12）写成矩阵形式有：

式中 M为质量矩阵；K为刚度矩阵；q为时间。

可以用戈辽金法、瑞利-瑞兹法或有限元法等数值方法求解方程的近似解。

2 有限元模型的建立

在忽略阻尼影响的情况下，有限元模型要求能够准确反映结构的质量分布特性和刚度分布特性。材料参数、单元类型和几何构型等均将影响结构的刚度分布特性，从而影响模态分析结果。此外，边界条件、连接件的预紧力等也将对结构的固有振动特性产生影响。以典型盖板式TPS的简化模型为例进行研究，构型如图4所示。

图4 典型盖板式TPS构型Fig.4 Typical Shingle TPS Structure

图4中模型主要由4个部分组成：C/SiC盖板、隔热层、机身蒙皮、连接件。具体尺寸及材料参数见表 1[6]，其中弹性模量均为室温下的参数，所用材料均为均质各向同性材料。

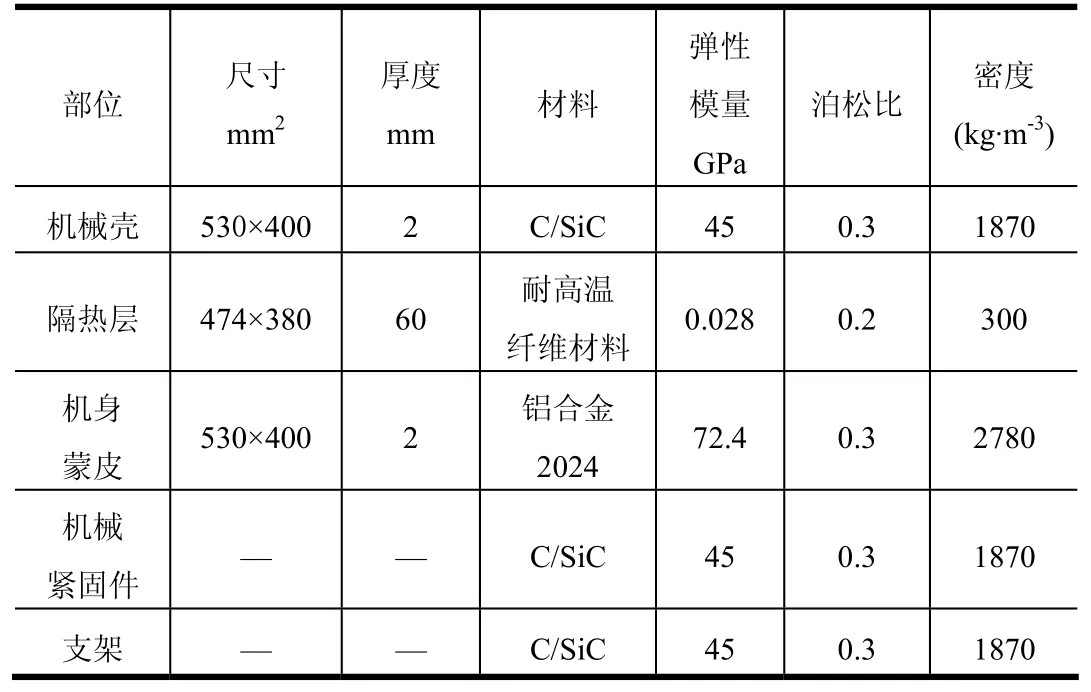
表1 尺寸及材料参数Tab.1 Dimensions and Material Physical Properties

2.1 单元类型

为建立合理的盖板式TPS有限元模型，下面将从赋予结构不同单元类型的角度开展分析。隔热层选用实体单元，机身蒙皮和盖板由于厚度非常薄可用实体单元也可用壳单元建模。分析模型如图5a所示，其中模型a中的单元全部为8节点六面体实体单元，单元总数为4800个（图6a）；在四边自由的边界条件下，利用Lanczos迭代法计算得到模态基频为263.68 Hz。模型b中盖板和机身蒙皮采用壳单元，隔热层选用实体单元，单元总数为4800个（见图6b）；边界条件为四边自由，经 Lanczos迭代法计算得到模态基频为254.26 Hz。

图5 模型示意Fig.5 Concepts of Model

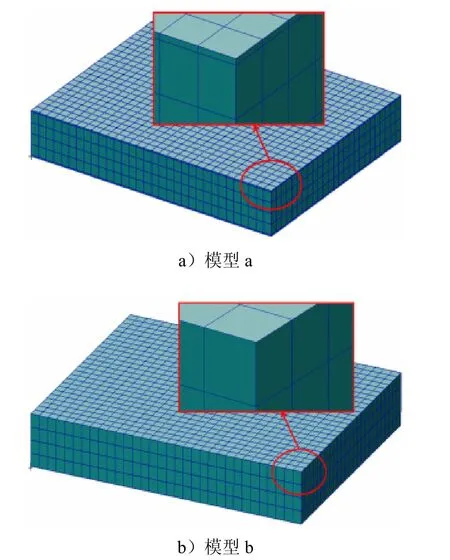
图6 模型的有限元模型Fig.6 Illustration of Finite Element Model

表2为模型质量统计结果，由表2可知，模型a和模型b的质量与实际质量相比存在误差，误差分别为 1%和 0.4%，这是由于结构被离散导致的。单元的一致质量矩阵为

式中 ρ为密度；N为单元位移插值函数矩阵；Ω表示体积；下角标e表示单元。

表2 模型质量统计Tab.2 Model Mass Details

而在计算模型a和模型b的模态基频时，单元质量矩阵为集中质量矩阵。集中质量矩阵是假定单元的质量集中在节点上，因而得到的质量矩阵是对角线矩阵，这将简化计算提高效率，并且对低阶频率的精度影响很小。

实体单元将单元一致质量矩阵eM转换为单元集中质量矩阵的一种常用方法如式（15）所示。

式中eV为单元的体积。

式中 下标 d为单元在几何空间的维数；W为单元的质量；dI为单位矩阵；eV为单元的体积。

壳单元将单元一致质量矩阵eM转换为单元集中质量矩阵的常用方法是忽略 M 中对应于转动自由

e度的元素。对于中与位移自由度相关的元素可采用式（15）进行处理。实际上，实体单元和壳单元集中质量矩阵的不同，本质上是由于节点自由度不同引起的，从而使得模型a和模型b的质量误差不同。本例中机身蒙皮和盖板采用壳单元质量分布特性更接近真实情况。

提取模型a和模型b中盖板和隔热层交界面相同位置角节点的刚度矩阵元素，位置在图5圆点处，节点编号为i。总体坐标下，由于模型a中全部为实体单元，每个节点有3个方向的自由度，而模型b由于有壳单元，其节点自由度为6。按节点划分结构的总刚度矩阵，提取的iiK如式（17）和式（18）所示。

式中 上标a和b为模型编号；下标i表示角节点编号。

因为节点位置为交界面的角点上，所以此节点只为交界面上下两个单元共用的节点。根据直接刚度法可知，的值是2个实体单元在角节点i处相应刚度元素的叠加；的值是1个实体单元和1个壳单元在角节点 i处相应刚度元素的叠加。观察矩阵可以看到和主对角线上的值基本在同一量级上，并且的刚度元素稍大。

2.2 装配建模方法

由图 4知此装配体为夹层结构，载荷主要通过上下板面接触及连接件传递。接触过程中2个物体在接触界面上的相互作用是复杂的力学现象，接触界面高度非线性。这种非线性来源于2个方面：a）接触界面的区域大小和相互位置以及接触状态事先未知，并且随时间变化，需在求解过程中确定；b）接触条件非线性，接触条件的内容包括：接触物体不可相互侵入；接触力的法向分量只能是压力；切向接触的摩擦条件。这些条件区别于一般约束条件，其特点是单边性的不等式约束，具有强烈的非线性[7]。

假设预紧力足够大使得连接件在振动过程中可以忽略非线性影响，按以往的工程经验这种连接属于紧密连接[8]，连接面两端位移可以认为是协调的，建模时可采用共节点方法或绑定接触模式进行装配建模。以模型b为例分别使用上述两种装配建模方法进行模态计算，结果如表3所示。共节点方法和绑定接触模式均是使装配体组件在接触面间不存在切向相对滑动或法向相对分离，但是在交界面上模拟力的传递方式不一样。

表3 不同装配建模方法计算结果Tab.3 Simulation Results of Modeling

共节点是通过直接刚度法，将下标相同的刚度元素叠加在一起，从而实现不同类型单元的结合。其物理意义是：整个结构抵抗某种变形的能力等于各单元抵抗该变形能力之和。

绑定接触模式则通过一定的接触算法实现力的传递，但计算时只需要迭代一次，属于线性接触类型，从而可在模态分析这种线性计算中使用。利用有限元分析软件ANSYS Workbench，在模型b的交界面生成接触单元CONTA 174和TARGE 170从而建立接触对，根据罚函数法进行接触计算。

罚函数法采用一个接触“弹簧”在两个面间建立关系，如图7所示，这个弹簧的刚度称为接触刚度[9]。在力F的作用下，弹簧被压缩Δ（侵入数值），且满足平衡方程

式中 k为接触刚度。

图7 罚函数法的接触弹簧Fig.7 The Contact Spring of Penalty Function Method

式中nK为法向接触刚度；nu为接触间隙大小。根据库伦法则，摩擦应力如下（zτ类同）：

式中sK为切向接触刚度；yu为y向接触滑动距离；μ为摩擦系数。

本算例中初始法向接触刚度和切向接触刚度分别设置为10 N/m2、1 N/m2。采用这种绑定接触模式的装配建模方法，计算出模型 b的模态基频结果为262.76 Hz。

在本算例中采用共节点和绑定接触方法对模型进行装配建模，由表 3可知采用这两种装配建模方法模态基频的计算结果相差不大。使用共节点方法进行装配时，要求相邻组件网格节点在交界面上一一对应，这将给各组件的网格划分带来限制，而使用绑定接触方法则不会带来这样的问题。但是采用绑定接触方法会产生接触单元，需额外进行接触计算，在求解全飞行器的动力学问题时将降低计算效率。

3 结 论

本文分别通过解析方法和有限元法建立了盖板式热防护结构的理论模型和有限元模型。建立理论模型的优点是物理量的意义简单直观，缺点是需进行大量简化与假设。虽然有限元法是高效且精确的工具，但是针对不同的结构需要重新建立不同的计算模型。对于文中算例，机身蒙皮和盖板采用壳单元模拟质量分布特性更接近真实情况；采用共节点和绑定接触方法对模型进行装配建模，模态基频的计算结果相差不大。文中对 C/SiC盖板式热防护结构动力学建模方法的研究，可为建立真实飞行器上的 C/SiC盖板式热防护结构动力学模型提供参考。