基于代理模型和线性近似的快速气动热边界求解方法

王 洋，袁军娅，王洪兴

（1. 北京航空航天大学，北京，100191；2. 航空工业第一飞机设计研究院，西安，710089；3. 北京卫星环境工程研究所，北京，100029）

0 引 言

高超声速飞行器一般是指飞行马赫数大于 5的飞行器，飞行器与大气剧烈摩擦，产生强烈的气动加热。同时与结构之间发生复杂的耦合作用。在流固耦合分析中，表面热流是流固边界传递的关键参数。高超声速气动热与来流条件（飞行高度、马赫数、攻角等）、表面温度和结构形状密切相关。目前，在高超声速流固耦合研究中，气动加热的计算方法主要分为工程计算和计算流体力学（Computational Fluid Dynamics，CFD）数值计算。工程算法基于边界层理论或者实验经验关系式，主要用于求解简单外形飞行器的气动热问题，对于复杂外形，由于其流场复杂，存在流动分离、激波-附面层干扰等现象，单纯的工程方法难以满足要求[1,2]。随着计算机和CFD数值计算方法的不断发展，已经能够针对复杂外形开展全尺寸三维流场仿真计算，但是效率仍旧较低，不能满足快速工程研制的需求。CFD降阶模型的研究成为解决这类高超声速气动热问题的一种有效途径，可以克服工程方法不够精确和CFD计算耗时的问题。

本文从两个方面着手，减少流固耦合分析中热边界的计算耗时。一方面应用本征正交分解（Proper Orthogonal Decomposition，POD）降阶代理模型，建立一种快速计算高超声速气动热的方法。另一方面引入基于换热系数的线性近似方法进行热边界传递，通过减少因壁温引起的流场计算迭代次数来缩短流固耦合计算时间。以三维翼面为例，验证了该方法有效性。

1 本征正交分解与代理模型

降阶就是利用一个简单的模型来代替CFD的来流条件和计算结果之间复杂的非线性关系，其中POD方法已经被很多研究人员采纳，并得到一定的成果。Burkardt等人[3]用该方法得到了N-S方程的降阶模型；Carlson和Roveda[4]将弱化形式的动量守恒方程投影到由速度相关的POD基函数形成的降阶空间，建立了一组低维的POD系数为状态变量的微分方程组来预测和控制翼面上的气动力，对 CFD和降阶模型（Reduced Order Model，ROM）的数据结果进行对比研究指出ROM利用少量的POD基模态能够准确地反映系统的动态特征。除此之外，POD方法还被应用在最优控制[5～7]、流体力学[8～10]、热传导[11,12]分析中，极大地缩短了计算时间，提高计算效率。

POD方法是一种将复杂系统分解为数个基本模态的方法，在基本模态中包含着原始系统的主要特征，利用少量的基本模态就可以表达复杂的原始系统的特征，得到原始系统的ROM。利用实验或者CFD数值计算得到一系列不同输入条件下的响应输出采用列向量的形式构成向量组，通过矩阵运算得到一组规范正交基，使得数据集合在这组基上的投影最大。通过对矩阵进行奇异值分解就可以得到正交基Φ以及特征值，由于矩阵S并非方阵，所以得到的特征值应该是方阵的特征值。特征值的大小表征了该特征值对应的特征向量，即POD基所包含的响应输出集合的特征的多少。通常通过广义“能”E来表征[13]前n个POD基所包含原系统特征的权重，广义能定义为

式中 λ为特征值；n为POD基的个数；k为系统样本点个数。

通常特征值从大到小衰减很快，这样广义能 E会趋近于1，前面几个POD基就能包含绝大部分的集合特征。通过对特征向量的个数进行截断，取前面部分基来表达整个系统，从而将全阶系统投影到低维空间。

代理模型的基本思想是通过数学方法，利用已有的输入和输出参数，构造出一个和原始计算结果相近的数学模型[14]。目前常用代理模型有多项式响应面模型、Kriging模型和径向基函数等，本文采用 Kriging模型。

式中 f(X)为回归模型，代表确定的函数； z(X)为一个均值为0，方差为σ2的随机过程，其协方差为

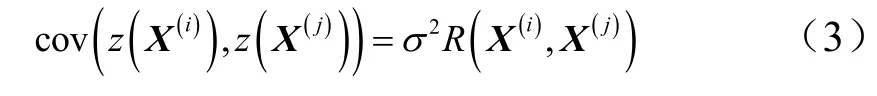
式中 R为两个输出参量 X(i)和 X(j)的相关函数，与两点在空间的位置相关，关系式为

其中，

式中 g为所有元素为1的向量。这样Kriging模型可以表示为

给定一个新的输入参数向量X，即可通过该模型预测输出参数。因此只需要将带约束的优化问题解决，得到θ，就可以构建出此模型来。一般通过遗传算法来求解最优的θ向量。

POD方法通过利用全阶模型计算结果建立一组最佳充分描述全阶系统动力学特性的正交基来描述系统的主要特性[16]。代理模型的目的是得到原系统样本点与截断后POD基投影系数的一一对应关系。本文以高超声速飞行器机翼气动热计算为例，建立POD-Kriging代理模型，过程包括：

a）选取马赫数、飞行高度和飞行攻角为设计变量，根据飞行轨道设计变量变化范围，确定设计变量空间，采用拉丁超立方试验设计方法在给定的变量范围内获得设计空间样本I=[Ma,α,H]。

b）采用数值计算方法得到各样本点对应响应输出，以表面热流为例，输出即为飞行器表面所有网格点给定壁温条件下的热流q，构建系统的特征矩阵

式中 n为样本点个数；m为网格点个数。

c）将系统矩阵Q进行奇异值分解，利用公式[15]：

对于给定样本空间范围内的任意计算状态，利用这个近似拟合关系得到POD基系数，从而得到q的近似响应值。

2 模型以及算例分析

2.1 模型和设计空间的选取

本文以战斗机 F-104机翼模型为例，分析基于POD-Kriging代理模型获得高超声速气动热的过程、精度和计算效率。该模型常被用来做高超声速分析，机翼相关参数如图1所示。

图1 机翼外形Fig.1 Shape of the Wing c—弦长

机翼外流场模型采用ICEM网格绘制软件划分，分为8个block，对机翼附近网格进行附面层加密，网格如图2所示，网格数为197.6万。

图2 机翼外流场网格Fig.2 Wing Outflow Field Grid

机翼的气动热设计变量和设计空间如表1所示。

表1 机翼气动热设计变量和设计空间Tab.1 Aerodynamic Heat Design Variables and Space of Wing

2.2 POD-Kriging代理模型的建立

在给定的设计空间内，经过拉丁超立方抽样，得到的100个样本点的初始来流条件，如表2所示。

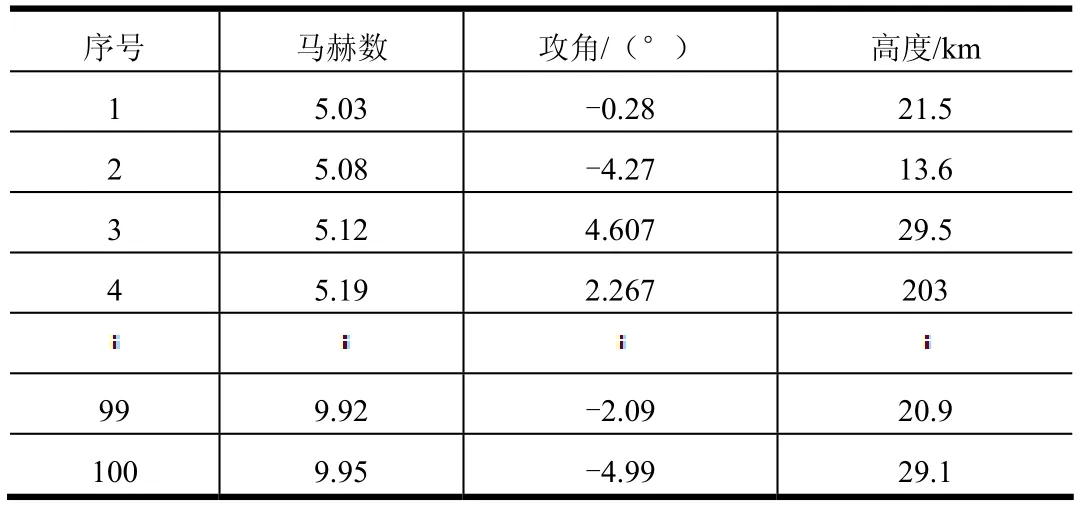
表2 样本点数据Tab.2 Sample Point Data

对于每一个样本点，本文采用CFD-Fastran软件计算翼面热流分布。CFD-Fastran常用于高超声速飞行器外流场计算，文献[17]通过数值计算与试验对比，得出结论CFD-FASTRAN软件的k-ε及B-L两种模型求解高超声速气动热问题均能达到较好的准确度，且 B-L模型计算速度快、使用方便。本文采用 B-L湍流模型，空间采用高阶AUSM格式，时间采用隐式迭代格式。以计算得到的不同来流条件下恒壁温的热流分布Q为基础，建立POD-Kringing代理模型。

2.3 代理模型计算结果分析

以热流Q为例，说明代理模型的计算精度。经过POD方法分解得到100个基模态的热流分布，图3为每一个基模态对应的特征值的对数曲线，特征值的大小表征了基模态对于热流分布的贡献，可以看出前10阶包含了大部分热流的特性。

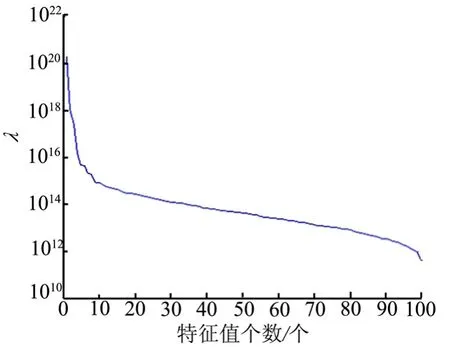
图3 基模态对应的特征值Fig.3 Eigenvalues of the Corresponding base Mode

2.3.1 典型工况算例分析

在给定的样本空间里随机取某一个测试点，进行CFD计算，然后与POD-Kriging代理模型的预测结果进行比较，在每个网格点进行相对误差计算，误差计算公式为

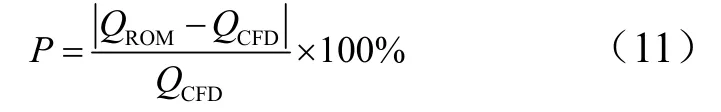
式中 ROM为用代理模型方法得到的热流预测值；CFD为用CFD-Fastran计算得到的热流值。

图 4为在流条件为飞行高度 H=20 km，攻角α=0°，马赫数Ma=7.5的情况下CFD计算的热流值与 POD-Kriging模型预测的热流值的相对误差分布。由图4可以看出，在机翼前缘处，二者的结果比较接近，在后缘部分，误差有所增加，误差最高的地方集中在前缘后部靠近翼根处，达到7%左右。结果表明，对于单个测试点，POD-Kriging代理模型的预测结果比较准确。

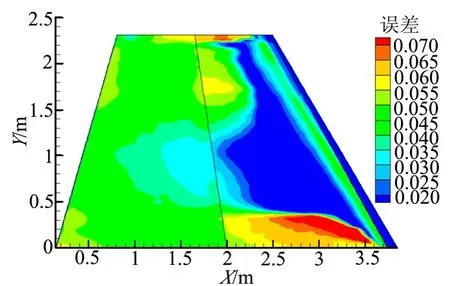
图4 马赫数为7.5来流翼面平均误差分布Fig.4 Average Error Distribution of the Wing Surface with the Maher Number of 7.5

2.3.2 测试样本点的相对平均误差

在输入参数的空间内随机选取10个测试样本点，测试样本点的输入参数如表 3所示。分别采用CFD-Fastran计算和代理模型计算热流分布，利用式（11）计算每个测试样本点的误差值Pi，10个样本点的相对平均误差为

表3 随机选取的10个样本点输入参数Tab.3 Input Parameters of Randomly Selected 10 Sample Points

用POD-Kriging方法得到的10个测试样本点的翼面热流平均相对误差云图，如图5所示。

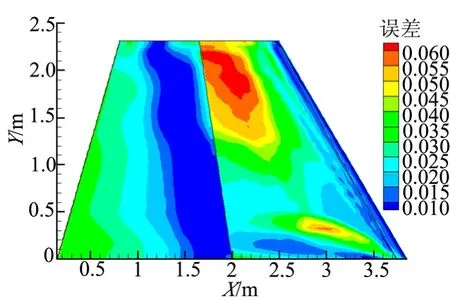
图5 10个样本点翼面热流密度平均误差分布Fig.5 Average Error Distribution of Heat Flow Density of Wing Surface at 10 Sample Points

从图5中可以看出，翼面误差基本小于6%，前缘处误差较小，误差较大的地方集中在上翼面凸起处和下翼面局部。

2.3.3 POD基模态个数影响

预测的准确程度与POD基模态的个数有关，图6显示的是基模态为15，20，25，30时，代理模型的热流预测值和CFD计算值的相对误差。

图6 不同基模态个数下平均误差分布的变化云图Fig.6 Variation of Mean Error Distribution under Different Fundamental Mode Numbers

由图 6可知，随着基模态个数的提高，平均误差逐渐变小，而且当基模态个数在20以后，平均误差的变化较小，误差最明显的地方集中在翼面凸起处，且最高误差在6%左右。

3 热边界线性化近似

3.1 热边界线性化近似方法

在一定样本基础上，通过建立 POD-Kriging代理模型，可以快速得到高超声速飞行器不同飞行条件下给定壁面温度的表面热流分布。而在一般的高超声速飞行器流固耦合研究中，通常会采用松耦合的方式，即将流场、固体结构场和温度场分开计算。以假定表面温度得到热流，再进行结构计算，不断迭代到误差在要求范围内。每一次CFD计算都要耗费大量的计算时间，给耦合仿真的工程应用带来困难。引入线性化近似的方法[18]可以改善CFD迭代耗时问题，即：传递热边界时，采用线性近似来计算新壁温条件下高超声速飞行器表面气动热，以代替CFD迭代计算热流，必要时再采用CFD或者代理模型迭代计算，某些情况下，这种近似在不进行CFD迭代的情况下也可以获得满足工程需要的计算结果。

热流计算表达式为

式中 h为换热系数；wT为壁面温度；awT为绝热壁面温度。

如果壁面温度对换热系数的影响较小，就可以以飞行器的换热系数和绝热壁温作为对象，建立POD-Kriging模型，那么热流就是壁面温度的线性函数。在耦合计算过程中，当表面温度变化时，可以通过换热系数和绝热表面温度直接得到变化后的表面热流，而不需要通过新的CFD计算得到表面热流。

建立绝热壁温的 POD-Kriging模型过程与建立热流的 POD-Kriging模型过程相同，只是样本点计算的响应输出是绝热壁温。建立换热系数的 POD-Kriging模型，需要同时计算定壁温表面热流和绝热温度来获得。

假设壁面温度与来流温度T∞相同时，表面热流为

忽略壁面温度对换热系数的影响，则换热系数可以通过下式计算：

对于每个样本点，需要计算壁温为来流温度的热流分布和绝热壁温分布，以此数据为基础，建立换热系数和绝热壁温的POD-Kriging模型。

3.2 换热系数误差分析

取来流条件为飞行高度 H=29.9 km，攻角α=0.9°，马赫数 Ma=9.08，采用CFD分别计算此条件下绝热壁面的温度分布awT和给定温度为300 K条件下的热流分布由式（15）求出换热系数1h。改变壁温为500 K，求出此时的热流同样求出换热系数对比热流和换热系数的变化。

图7为改变壁温前后，各网格点的热流变化。

图7 改变壁温引起的热流的变化Fig.7 Change of Heat Flux Caused by Wall Temperature

图8为换热系数在温度改变前后的变化。

图8 改变壁温引起换热系数的变化Fig.8 Change of Heat Transfer Coefficient Caused by Changing Wall Temperature

由图7、图8可以看出，与对热流的影响相比，温度变化对于换热系数的影响较小，变化率在6.5%以内。

温度改变后，由式（13）利用线性化方法求解新的热流，与CFD得到的热流进行比较，图9为二者计算热流结果的相对变化。

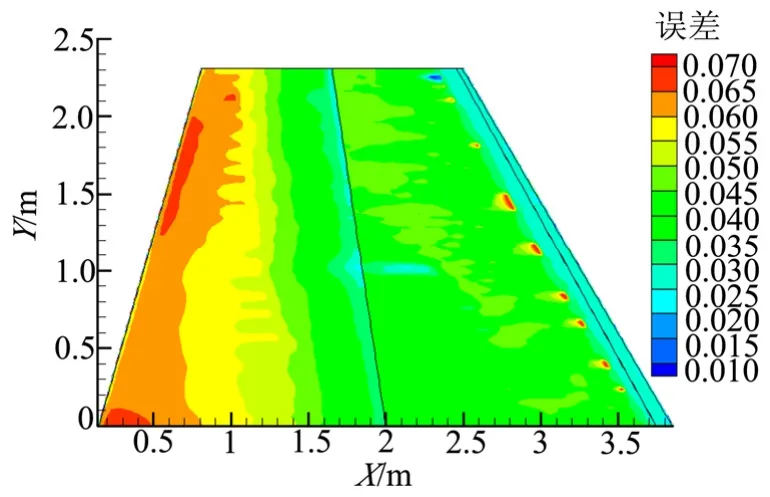
图9 线性化处理和CFD结果的相对变化Fig.9 Relative Change of Linearization and CFD Results

由图9可以看出，线性化处理得到的壁温变化后热流与CFD计算结果相对误差基本在7%以下。在计算过程中，CFD计算一次需要10 h以上，而采用线性化处理只需不到1 s，极大提高了计算效率。

3.3 代理模型结合线性化近似结果分析

取飞行高度 H=29.9 km，攻角α=0.9°，马赫数Ma=9.08作为来流条件，利用POD-Kriging代理模型快速计算该状态下冷壁热流和绝热壁的温度，再利用式（13）可以求出壁温改变为500 K后的表面热流，同时采用CFD-Fastran计算壁温改变为500 K后该状态的表面热流，图10显示的是二者的相对误差。从图10中可以看出，前缘误差较小，在2.5%以内，后缘误差较大，整个翼面的误差值在7%以内。和图9相比，误差较大的网格点有所增多，这是因为绝热壁温是经过POD代理模型的预测值，增加了误差。

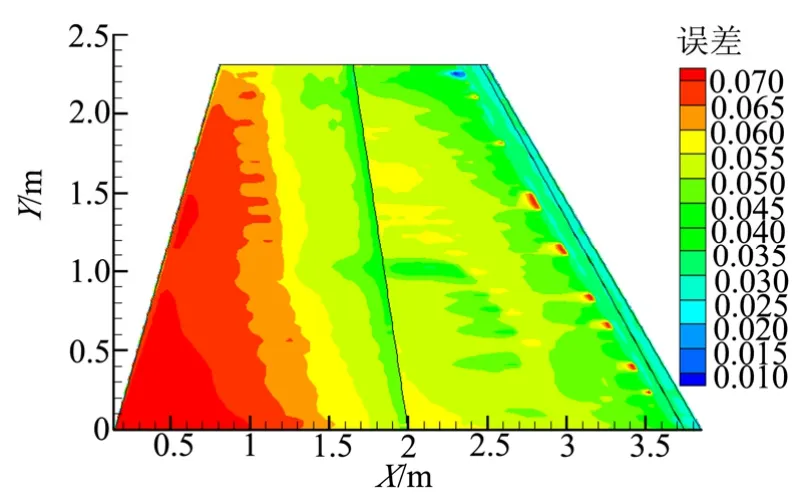
图10 POD-Kriging模型和CFD结果的相对误差Fig.10 Relative Error of the POD-Kriging Model and the CFD Result

4 结 论

本文以减少流固耦合过程中热边界的求解时间为目标，一方面基于 POD-Kriging代理模型建立快速计算不同状态的气动热参数分布的方法；另一方面提出基于换热系数的线性近似方法确定热边界，以三维机翼为例，分析了方法的可行性，得到以下结论：

a）对高超声速飞行器机翼气动热提出的POD-Kriging代理模型结合的方法，成功实现模型的降阶，代理模型的热流计算误差在7%之内；

b）在POD-Kriging建模过程中选取的基模态个数对代理模型预测结果会产生影响，结果表明增加基模态个数在一定程度上能够提高预测精度，当其达到20后，预测误差变化很微小；

c）引入换热系数线性近似的方法，能够节省耦合计算过程中因壁温变化引起的流场迭代步骤，在不降低热流计算精度的前提下，可以缩短计算时间。

本文建立的方法在满足一定计算精度的条件下，极大地提高计算效率，促进高超声速飞行器再入过程中的流固耦合分析或多物理场优化设计的工程应用。