学生“准代数思维”培养琐思

刘爱霞

“准代数思维”是介于“算术思维”和“代数思维”之间的桥梁和纽带。培养学生的“准代数思维”是数学教学的应有之义。在数学教学中，通过生活化孕育、数学化活动和反思性审视，可以启蒙学生的关系思维、引发学生的符号思考、丰厚学生的代数思想。

众所周知，小学阶段的数学学习主要是“算术”，而初中阶段的数学学习主要是“代数”。因此，许多教师对数学、数学教学的认识和实践都存在误区，比如认为小学低、中年级无须渗透代数思维，无须过早地涉及符号，等。在数学教学中，教师应该播种符号意识，启蒙学生的“准代数思维”。

一、生活化孕育，启蒙学生的关系思维

如果说，算术思维是一种程序性思维，那么准代数思维就是一种变量思维、关系思维。美国著名数学家卡彭特认为，“由算术思维到代数思维重要转换标志之一就是从等号的程序观念到等号的关系观念的转变。”生活中孕育着丰富的关系模型，比如跷跷板、天平等。教师要引领学生借助生活原型理解数量之间的关系、理解变量，让学生的生活、经验与代数学习相互匹配、无缝链接，进而能够建立准代数模型，发展学生准代数思维。

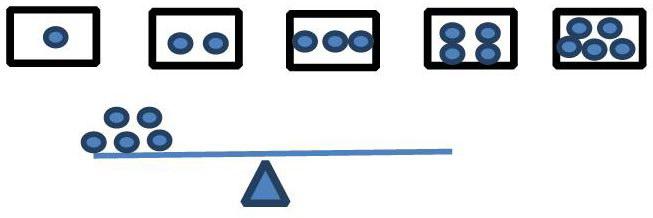
以苏教版小学数学教材为例，一直到五年级下册学习“简易方程”，才重拾起等号的关系性作用。其实，在小学低年级数学教学中，教师就可以有意识地结合学生的生活经验，帮助学生形象地建构等号的关系观念。如在小学一年级学习“整数的分与合”时，就可以借助学生熟悉的天平、跷跷板等（如图），帮助学生形象地建立数学模型。

学生根据玩耍跷跷板的生活经验，能够选择相应的点数填入跷跷板右侧的问号处。如5=5、5=1+4、5=2+3。不仅如此，在教学中，教师还可以启发学生：跷跷板两边的数可以交换吗？学生根据玩耍跷跷板平衡的生活经验，能够发现如果跷跷板保持平衡，跷跷板两边的数就可以交换。如此，整数的合成学习就自然地转变为整数的分解学习。这为学生在四年级学习整数加法乃至乘法的交换律奠定了坚实的基础。

如此，学生对算式本身有了一种整体性、结构性的把握。

二、數学化活动，引发学生的符号思考

英国著名数理逻辑学家罗素曾经这样说：“什么是数学？数学就是符号加逻辑。”的确，作为数学的准代数化，一个明显的标志就是学生数学学习的符号化。因此，在数学教学中，教师需要对学生进行积极的符号启蒙，通过符号孕育、符号播种、符号创造等，引发学生的符号思考。比如对于这样的文字题：“比一个数的4倍还少4是156，这个数是多少？”不少学生在学习中，总是受到文字题中的关键文字，比如“多”“少”等影响，而出现各式各样的错误，如（156+4）×4、（156+4）÷4、156-4÷4等等。显然，学生缺乏数学化活动，没有对文字题展开深度分析，更没有形成良好的符号意识和运用符号进行思维的能力。笔者在教学中，一方面引导学生画线段图，让学生借助线段图理解1份数、4份数等，然后理清它们之间的相等关系，列式解答。另一方面，引导学生进行符号分析，如将一个数看成小括号，这样，复杂的文字题就被浓缩、改装成简约的符号算式——“（）×4-4=156”，将一个数看成字母△，这样就形成了类似方程的符号模型——“△×4-4=156”，等等。著名的数学家莱布尼茨说：“符号的巧妙和符号的艺术，是人们绝妙的助手，因为它们使思考工作得到节约。在这里它以惊人的形式节省了思维。”与文字不同，数学符号具有简洁、形象、直观、概括等特性。数学教学中，通过渗透、播种、启蒙学生的符号意识，敏锐学生的符号感觉，激发学生的符号思考，让学生经历数学符号产生、建构、运用的全过程。通过符号化的数学活动，发展学生的“准代数式思维”。

三、反思性审视，积淀学生的代数思想

法国著名思想家笛卡尔曾经这样说：“任何问题都可以转化成数学问题，任何数学问题都可以转化成代数问题，任何代数问题都可以转化为方程问题。”教学中，教师要引领学生不断地进行数学反刍、数学反省、数学反思、数学批判，不断地积淀、丰富学生的代数思想。

比如在五年级数学学习中，学生遇到了一道探索规律的题目：用小棒摆正方形，摆1个正方形需要4根小棒；摆2个正方形需要7根小棒，摆3个正方形需要10根小棒，摆10个正方形需要几根小棒？摆100个正方形呢？100根小棒能够摆几个正方形呢？（如图）

在探索规律的过程中，学生不断地对小棒图进行审视、反思，形成了基于不同思维方式的多种算式。如有学生以1根小棒作为起始，一个正方形就是1+3，两个正方形就是1+2×3，三个正方形就是1+3×3……；有学生以一个正方形作为起始，这样一个正方形就是4，两个正方形就是4+3，三个正方形就是4+2×3……；有学生从正方形的个数上展开思考，一个正方形是4，两个正方形是2×4-1×2，三个正方形是3×4-2×2……；有学生以上下左右线段为参照，如一个正方形是2+2，两个正方形是2×2+3，三个正方形是2×3+4……。

在学生对小棒图进行多向审视（左右看、上下看、整体看等）中，形成了多样化的数学表达。如4+3×（n—1）、1+3n、2n+（n+1 ）、n+2（n+1）……在不断地符号化审视中，学生不断地建构，有效地积淀起学生的符号化能力、代数化思想。

这个过程是一个循序渐进、缓慢生长的过程。

培育学生的“准代数思维”是数学教学的应有之义。为此，教师要不断地捕捉学生问题思考、问题解决过程中的“代数的种子”，既向学生呈现“算术程序或步骤”，又向学生呈现“代数关系或结构”。让学生运用“代数的耳朵”和“代数的眼睛”初步思考问题、尝试解决问题。学生在学习抽象、概括、验证、建模以及预测等的过程中，逐步地形成“准代数素养”乃至“代数素养”。