分数阶连续线性系统基于观测器的H∞状态反馈控制器的设计

王振芳，罗 芳,马瑞青

(1.山西大同大学数学与计算机科学学院,山西大同037009;2.山西师范大学数学与计算机科学学院,山西临汾041004)

在控制系统的设计过程中，一般是设计各种满足一定性能指标的状态反馈控制器，然而在实际控制系统中，很多时候状态是不易测量的，从而使得状态反馈控制器难以实现其物理意。为了解决这一问题，我们将采用状态观测器来获得系统状态的估计值，设计出基于观测器的H∞状态反馈控制器.文章主要在文献[1]的基础上对分数阶连续线性系统的基于观测器的H∞状态反馈控制器进行研究。

1 系统描述

考虑如下分数阶连续线性系统

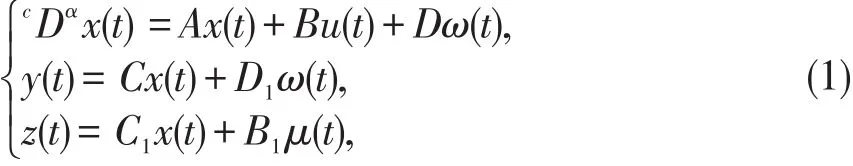
其中，1≤α＜2,x(t)∈Rn为系统状态变量，μ(t)∈Rm为控制输入变量，ω(t)∈Rp为外部干扰输入变量，y(t)∈Rq为测量输出变量，z(t)∈Rr为控制输出变。系统矩阵A,B,B1,C,C1,D,D1为适当维数的矩阵。

下面给出分数阶连续线性系统(1)有关的一些定义及一些引理。

引理1对于任何矩阵 Δ∈Rm×n,且 rank(Δ)=m,则存在Δ的奇异值分解

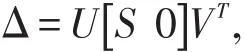
其中，S∈Rm×m是对角矩阵，U∈Rm×m,V∈Rn×n为正交矩。[2]

引理2给定矩阵 Δ∈Rm×n,且 rank(Δ)=m,假设X∈Rn×n是对称矩阵，则存在矩阵满足的充要条件是X可以写成

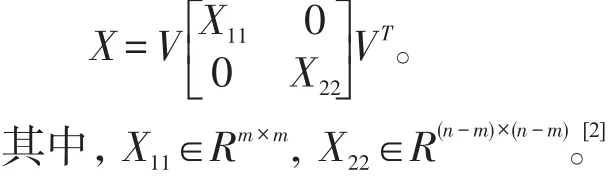
2 问题陈述

对分数阶连续线性系统(1)，采用如下基于观测器的控制器

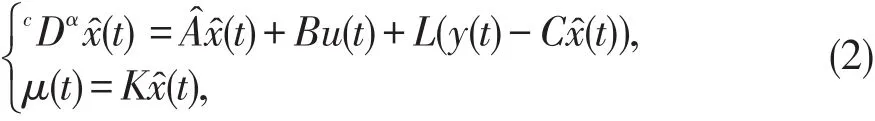
定义增广状态变量

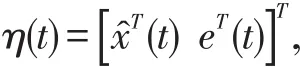
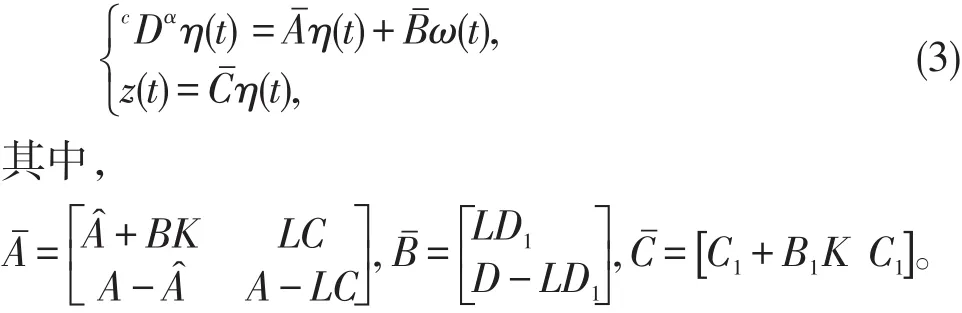
文中所研究的基于观测器的H∞状态反馈控制器设计问题可陈述如下：对于分数阶连续线性系统(1)设计形如(2)的控制器使得闭环系统(3)渐进稳定且满足H∞性能指标。

引理3给定扰动水平γ＞0，闭环系统(3)渐进稳定且满足H∞性能指标的充要条件为存在矩阵P＞0[3]，使得

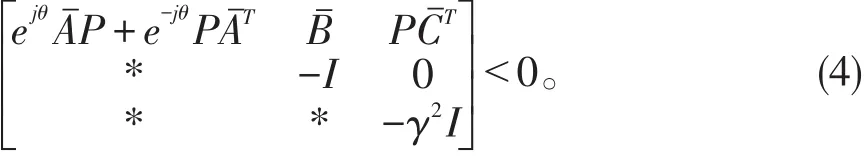
3 主要结果

首先给出闭环系统(3)渐进稳定且满足H∞性能指标的充分条件，其次通过使用矩阵奇异值分解的方法，以线性矩阵不等式形式给出了基于观测器的H∞状态反馈控制器存在的充分条件。

定理1给定扰动水平给定扰动水平γ＞0，闭环系统(3)渐进稳定且满足H∞性能指标的充分条件为存在矩阵P1＞0,矩阵P2＞0,矩阵K,L使得

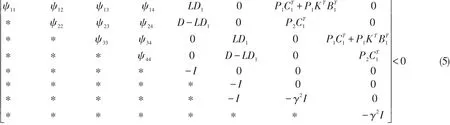
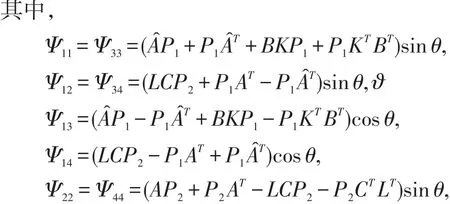
则不等式(5)可以写成不等式

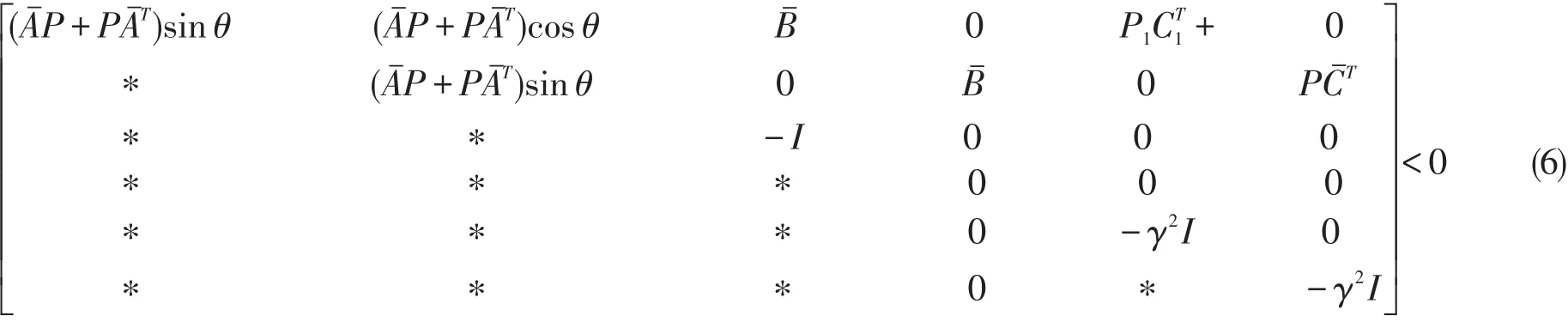
设矩阵(7)特征值为λ，即

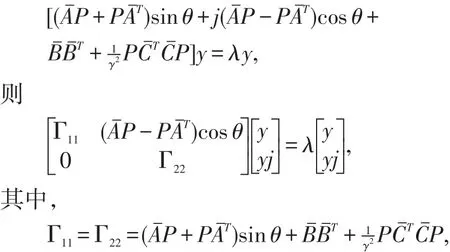
即矩阵(7)与矩阵

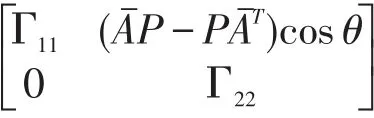
有相同的特征值。则不等式(4)等价于不等式

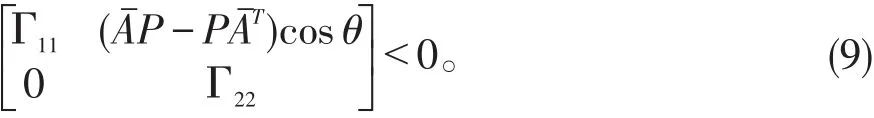
根据Schur补引理，不等式(9)等价于不等式(6)。证明完毕。

由于存在非线性项BKP1,LCP2,因此，矩阵不等式(5)不是线性矩阵不等式。下面应用引理1和引理2将它转化为线性矩阵不等式。

定理2对于分数阶连续线性系统(1)，假设输出矩阵C行满秩，则存在矩阵C的奇异值分解

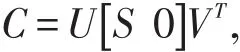
此时基于观测器的H∞状态反馈控制器存在的充分条件为存在矩阵 P1＞0,矩阵 P11＞0,矩阵P22＞0,矩阵 M,X1和 X2使得

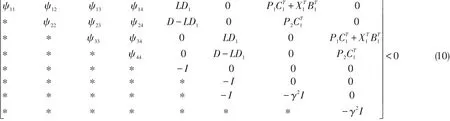
证明由于

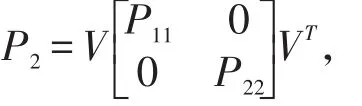
注:定理2给出了分数阶连续线性系统(1)的基于观测器的H∞控制器的线性矩阵不等式，

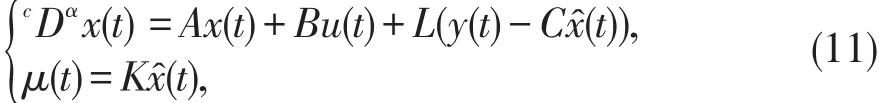
推论1对于分数阶连续线性系统(1)，假设输出矩阵C行满秩，存在矩阵C的奇异值分解

则基于观测器的H∞状态反馈控制器存在的充分条件为存在矩阵P1＞0,矩阵P11＞0,矩阵P22＞0,矩阵M,X1和X2使得

其中，

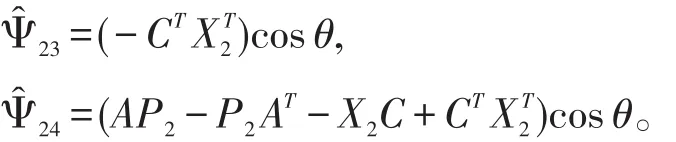
4 数值例子

例考虑如下分数阶连续线性系统

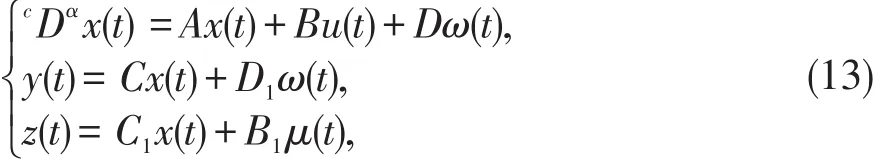
其中，α=1.7,

解求解线性矩阵不等式(10)，且令γ=0.145,可得