基于结构分解的动态图增量匹配算法*
许 嘉,张千桢,赵 翔,吕 品,李陶深,2
1.广西大学 计算机与电子信息学院,南宁 530004
2.广西高校并行分布计算技术重点实验室,南宁 530004
3.广西多媒体通信与网络技术重点实验室,南宁 530004
4.国防科技大学 信息系统与管理学院,长沙 410073
1 引言
随着信息科技与互联网的快速发展,数据规模不断增长,数据类型不断增多,不同领域关注的实体对象之间的关系变得更加复杂,如何分析和挖掘大数据中蕴含的复杂关系吸引了诸多研究学者。图(graph)作为一种广泛使用的数据结构,图中的每个节点代表现实世界中的实体对象,节点之间的边表示实体之间的关系,适合描述上述这种存在有内在复杂关系的数据。子图模式匹配返回数据图中所有和给定模式图相同或相似的子图,是分析和挖掘图数据的重要查询操作,具有众多实际应用。例如在社交网络(新浪微博、微信等)中,子图模式匹配通常用于挖掘目标客户团体[1];又如在生物分析领域中,子图模式匹配可用于对未知性质的蛋白质进行辅助分析[2]。
然而在现实世界中,描述实体对象图数据的结构和内容往往会随着时间的推移发生变化。例如社交网络中,2010年Facebook网站的用户从3.37亿人增加到5.85亿人,平均每分钟都会有47 553对好友之间建立或者解除关系;2011年,Google+在上线后的两周时间增长了1 000万的用户[3]。生物分析领域中,蛋白质与酶会发生复杂的交互与代谢关系,导致蛋白质的结构发生变化。这些数据表明,现实世界中的实体对象和它们之间的关系无时无刻都可能经历着变化。如果每一次变化都重新对如此大规模的数据图进行一次完整的图模式匹配必然耗费大量的时间和资源。由此可见,研究动态图的增量图模式匹配算法具有重要的意义,因为其能够利用前次匹配结果,快速得到数据图动态更新后变化的匹配结果。
本文设计与实现了面向动态数据图的增量图模式匹配算法,主要贡献如下:
(1)提出了一种基于图结构分解的动态图增量匹配算法框架,通过记录中间结果并构建匹配所需的索引,加速后续图模式匹配的执行效率。
(2)基于前次匹配结果和维护的索引信息,将数据图中增加的边事件进行分类,并为每类增加边事件设计相应的增量匹配算法,快速更新模式图和数据图间的模式匹配结果,有效减少重复计算。
(3)在真实数据上对本文提出的算法进行全面测试,验证了所提算法的有效性。结果表明本文提出的面向动态数据图的增量图模式匹配算法比目前最好的增量匹配算法在执行效率上平均提升了1~2倍。
2 相关工作
2.1 图模式匹配
子图模式匹配通常采用基于回溯的方法或基于探索的方法实现。基于回溯的方法首先根据节点的标签为模式图的每一个节点生成一个匹配候选集,然后根据一个匹配顺序来连接这些候选的匹配点,得到最终匹配结果。该方法中匹配顺序直接影响子图匹配效率[4-5]。基于探索的方法是从数据图的一个节点出发,根据模式图指定的节点之间的关系对数据图进行探索式匹配,即检测访问的数据图节点是否满足模式图的匹配要求[6-7]。
子图同构是NP完全问题,在子图匹配的过程中,当迭代匹配模式图中的每一个节点时,会产生很多无效的中间结果,影响匹配效率。针对这类问题,VF2[8]和QuickSI[4]技术利用模式图的连通性特征对候选集进行剪枝,提高静态图上的模式匹配效率。TurboISO[9]技术通过将模式图中具有相同标签和相同邻居的节点进行合并来减少无效候选对象的产生。除此之外,另一个关键问题是找到一个有效的图节点匹配顺序。QuickSI[4]技术采用稀有标签优先策略对模式图节点进行排序,首先处理在数据图中出现频次较低的节点。SPath[5]技术采用稀有路径优先策略对模式图节点进行排序,当模式图规模增大时这类方法的执行效率将随之降低。Bi等人提出在子图匹配的过程中,除了相似节点之外不相似节点也会导致冗余的笛卡尔积,并产生无效的中间结果[10]。Bi等人因而提出了一种查询分解的策略,将模式图分解为核心、森林和叶子三部分,并按照该顺序进行模式图匹配处理。由于核心部分的剪枝能力最强,其次是森林以及叶子部分。基于该顺序进行匹配可将笛卡尔积操作拖延到叶子节点进行,有效减少冗余笛卡尔积的产生,从而达到进一步约减查询候选集。
2.2 增量图模式匹配
对于数据图发生变化的情况,文献[11]提出了快速不精确图模式匹配算法及增量算法,将子图查询问题转化为向量空间关系检测,用近似的方法确定在一组图流中是否包含给定的模式图。当数据图增加或者删除边时,修改相关节点的向量,然后重新检查新的向量是否包含模式图的向量来确定匹配状态。然而,重新检查仍然意味着对完整的数据图进行匹配,影响匹配效率。文献[12]提出了一种增量图计算的匹配思想,根据数据图的变化和匹配的影响区域(等于模式图直径)确定潜在会产生匹配结果的图节点集并进行重新匹配,但是随着模式图规模的增大,影响区域范围也会相应增大,算法效率大幅度下降。研究发现,当模式图较大时,如果数据图每次更新都需要对整个模式图进行查找将浪费大量时间,因此可将模式图进行分解。文献[13]将模式图分解为一系列单边或者双边子图,并按照选择度的高低进行排序,优先匹配选择度高也即识别能力强的边,有利于减少中间结果。然而由于分解特征相对简单,当模式图较大时,仍会产生大量中间结果,影响算法效率。文献[14]提出了一种基于连接与基于探索相结合的匹配算法,将模式图按照单汇点有向无环图(single sink directed acyclic graph,SSD)进行分解,然后在每个子图中将节点信息的传递规则映射到数据图中,从而找到数据图更新后变化的匹配结果。这种方法主要适用于分布式环境,不能直接运用于单机环境。上述所有增量算法的设计思路基本一致:根据数据图的变化确定可能受影响的区域,对受影响的区域进行重新计算,得到数据图更新后变化的匹配结果。
上述面向单机环境的增量算法只能有效处理规模较小的模式图,当模式图增大时算法效率将显著降低。本文提出一种基于结构分解的精确子图匹配算法,利用增量计算的思想基于之前的匹配结果进一步约减数据图动态变化时的受影响区域,从而有效提升算法匹配规模较大的模式图的执行效率。
3 动态图匹配问题的形式化描述
本文研究的模式图和数据图是带有标签的无向图,每个节点只有一个标签,标签决定节点属性。
定义1(动态图)已知初始数据图G=(U,E,L),U是图节点集,E⊆U×U是边集,L是一个标签函数,U中每一个节点都有一个标签。引发数据图更新的操作可以用一个三元组<op,ui,uj>来表示,其中op={I,D}用来表示边的增加或者删除操作,I表示增加边,D则表示删除边,ui和uj表示数据图中的两个节点。数据图中增加一个新的节点可以用一系列跟该节点相关的增加边操作来表示。与此类似,删除一个节点可以用一系列跟该节点相关的删除边操作来表示。给定一个数据图G上的更新操作集合C={<op1,u1,u2>,<op2,u2,u3>,…,<opk,uk,uk+1>}(k≥ 1),G′则表示数据图G基于操作集合C更新后的数据图。
定义2(动态图模式匹配)已知模式图P(Vp,Ep,Lp),数据图G和数据图的更新操作集合C,动态图匹配问题是指模式图P与执行更新操作C后的数据子图Gsub-t=(Vsub-t,Esub-t,Lsub-t)之间存在一个双射函数f,满足:
其中f(v)表示数据图G中与模式图节点v满足双射关系的节点,即数据图中与节点v相匹配的节点。数据图中所有跟模式图匹配的节点及它们之间的边可构建出匹配的结果图Gr。
4 基于结构分解的增量匹配算法
增量算法是指在数据图发生变化后,利用现有的匹配结果以及数据图的变化来得到新增加的匹配结果,这样可以最大限度地减小重复计算。在增量匹配过程中,使用索引可以快速缩小搜索空间。建立的索引越多,增量匹配的搜索空间越少,找到新增加的匹配结果的时间也会越少,但是存储和维护索引的开销也越大。为了限制索引存储和维护开销,本文仅为模式图构建以下两类集合作为索引:
(1)match(·)集合:给定模式图中任一节点v,match(v)表示数据图中跟v匹配的节点集合,match(·)集合中所有的点都在匹配的结果图中。
(2)candt(·)集合:给定模式图中任一节点v,candt(v)表示数据图中除了match(v)之外,标签跟v相同的节点集合。
4.1 Inc_CFLS(incremental core-forest-leaf solution)算法基本框架
基于文献[10]提出的核心-森林-叶子(core-forestleaf,CFL)结构分解框架,本文将模式图分解为核心、森林和叶子三部分,如图1所示。
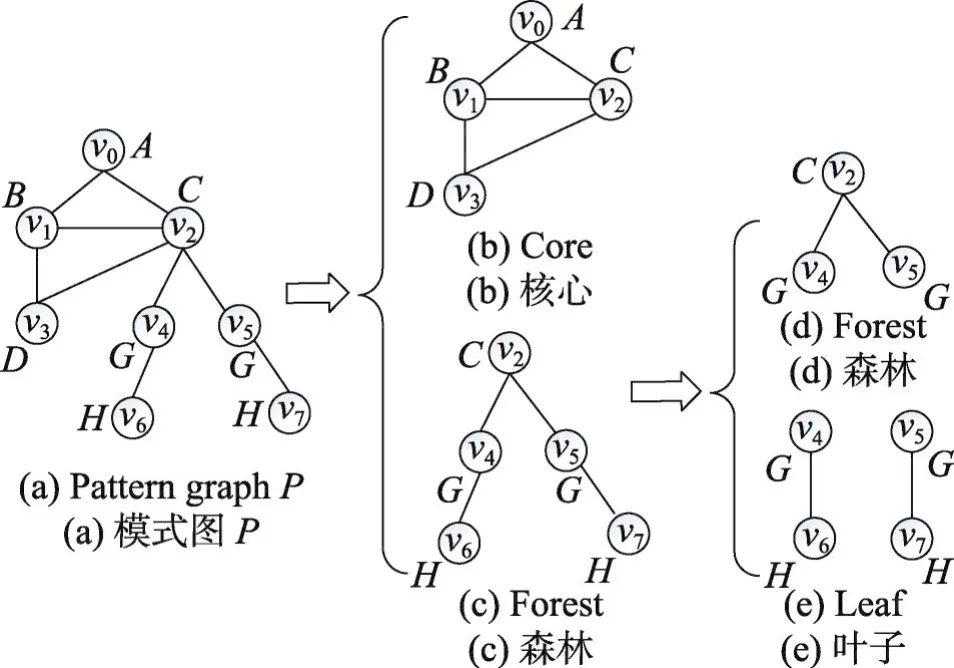
Fig.1 Core-Forest-Leaf decomposition图1 核心-森林-叶子分解
其中核心部分是指模式图中的密集子图,图中每个节点的度都大于1。核心结构具有较高的识别能力,在子图匹配的过程中,首先对核心结构进行匹配可以约减查找空间。其次,对每一部分按照基于路径的方法制定了一个查询匹配顺序,将模式图节点按照制定的顺序进行匹配可以进一步约减无效的中间结果。文献[10]采用的方法是面向静态图的模式匹配,本文在此基础上提出了面向动态图的增量匹配算法,称为Inc_CFLS。
本文所提出的增量图模式匹配算法的基本框架如图2所示。
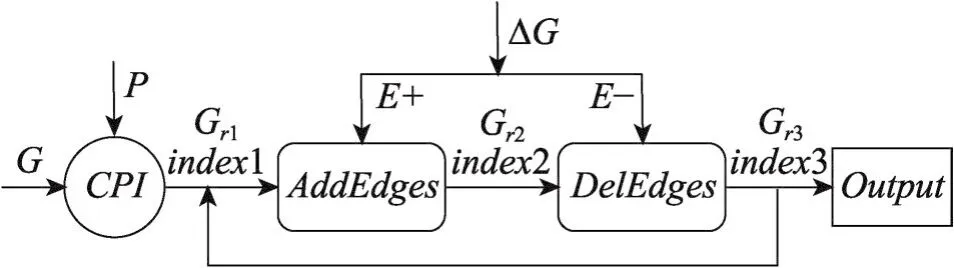
Fig.2 Basic framework of Inc_CFLS algorithm图2 Inc_CFLS算法的基本框架
首先使用文献[10]提出的CPI(compact pathbased)算法,用于第一次在整个数据图G上对模式图P进行匹配,一方面获得匹配的结果图Gr1,另一方面建立后续增量匹配所需要的索引index1。对数据图的更新,表示为ΔG,可以分为“增加边”(E+)和“删除边”(E-)两部分。首先对增加的边调用算法Add-Edges,获得匹配结果图Gr2以及更新后的索引index2;接着调用算法DelEdges,获得匹配结果图Gr3和更新后的索引index3。根据匹配结果图Gr3可得到数据图更新后所有与模式图相匹配的子图,并完成结果输出。index3可用于后续的增量匹配,即在下轮匹配中用上轮得到的index3替换本轮的index1即可。DelEdges算法是一个对结果图的精简过程,且目前的研究方法基本相似,因此本文重点考察对数据图“增加边”的操作,详细阐述面向数据图增加边的子算法AddEdges。
4.2 面向数据图增加边的子算法AddEdges
研究发现,当模式图为树型结构时(如图3(a)),可以利用树结构的特性来进一步缩小匹配的影响区域。为模式图中的每个节点v,产生match(v)和candt(v)这两个集合作为索引,例如match(v0)为u1,u2。并根据match(·)集合中的节点及它们之间的边构建出匹配的结果图Gr(如图3(b))。
影响区域是指数据图变化引起的结果图Gr中可能会发生变化的索引match(·)对应的模式图节点。根据文献[10]提出的CPI算法找到模式图中的根节点(root),并按照宽度优先搜索确认模式图中每一个节点所处的层次(level)。
对于每一条新增加的边(u,u′),首先需要判断模式图中是否存在一条边(v,v′)与其相匹配,默认level(v)<level(v′)。以图3中的模式图为例,若 (v2,v4)与其相匹配,则需要对(u,u′)进行分类讨论来确定影响区域。
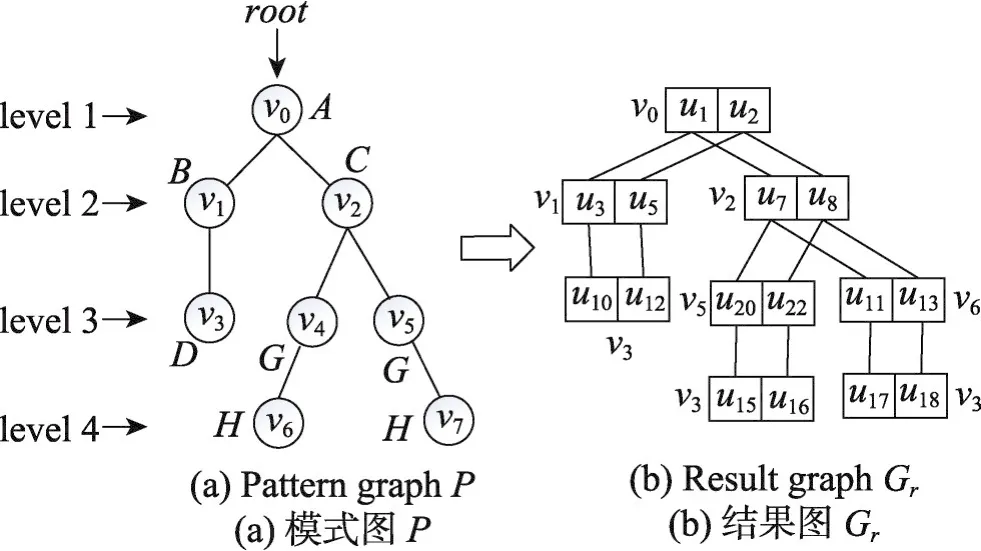
Fig.3 Corresponding result graph of pattern graph P图3 模式图P对应的结果图
(1)u∈match(v2),u′∈match(v4)(MM):此时只需将结果图Gr中的节点u,u′相连即可,不会引起索引的更新。
(2)u∈match(v2),u′∈candt(v4)(MC):此时的影响区域为模式图中以节点v4为祖先的所有节点(affected area of MC,AFF_MC),也就是v6。证明如下:如果非影响区域(v0,v1,v3,v5,v7)中对应的索引发生变化,且满足匹配条件的话,则在增加边(u,u′)之前,该部分产生的匹配结果就可以与剩余部分结合产生新的匹配结果。因此非影响区域索引变化产生的匹配结果在增加边(u,u′)之前就已经在结果图Gr中,增加边(u,u′)不会引起非影响区域索引发生变化。
(3)u∈candt(v2),u′∈match(v4)(CM):首先找到以节点v4为祖先的所有模式图节点(此例为v6),然后将这些节点以及节点v2、v4删除,剩余部分就是影响区域(affected area of CM,AFF_CM),证明同上。
(4)u∈candt(v2),u′∈candt(v4)(CC):此时的影响区域为模式图中除了v2、v4的所有节点。在子图匹配的过程中,若影响区域中节点v6的候选集节点u6满足u6∈match(v6),则可以将u6从v6候选集中删除,因为u6不会引起后续产生新的匹配结果,证明同(2)和(3)。
综上所述,当模式图为树型结构时,增加边(u,u′)可以迅速确认影响区域,减小查找空间。基于此,给出数据图增加边时的处理算法AddEdges的基本设计思路:
(1)对于任意给定的模式图P,首先找到其对应的生成树PT,如图4所示。其中模式图P中的边可以分为两部分:一部分是在生成树PT中的边,称为tree边;另一部分是不在生成树中的边,称为non-tree边。
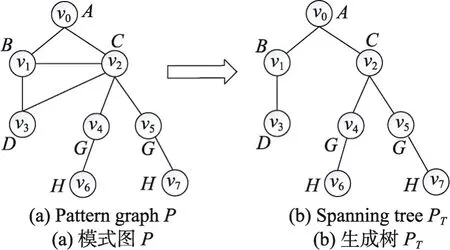
Fig.4 Corresponding spanning tree PTof pattern graph P图4 模式图P对应的生成树PT
(2)将PT作为模式图,在整个数据图G上进行图模式匹配,得到每个节点对应的索引match(·)和candt(·),以及匹配的结果图GT。
(3)当增加一条边(u,u′)时,判断模式图P中是否存在一条边(v,v′)与其相匹配,若存在,则需继续对(v,v′)的类型进行讨论。当 (v,v′)为tree边,可以直接根据(u,u′)的类型来确定匹配的影响区域。当(v,v′)为non-tree边时,由于在PT中不存在non-tree边,此时相当于在PT中增加了一条边。模式图增加边后只会导致匹配结果减少,因此只需判断v和v′对应的match(v)和match(v′)中是否有u、u′即可,如果没有则直接删除该候选对象。
(4)当增加完所有的边之后,利用non-tree边进行剪枝,将结果图GT中不满足non-tree边关系的部分删除,即可得到模式图P对应的结果图Gr。
在子图匹配方面采用基于相邻节点关系的匹配方式,由于PT是树结构,可以将PT分解为森林和叶子两部分,然后根据CPI算法得到每一部分的匹配顺序。当增加的边的类型为MC,此时只需对影响区域中的节点按匹配顺序进行匹配即可。在匹配过程中,若影响区域中节点v″的候选集节点u″满足u″∈match(v″),则可以将u″从v″的候选集中删除,因为u″不会引起后续产生新的匹配结果。当增加边的类型为CM时,首先从节点v开始,按照level递减的方向找到一条到根节点的路径进行匹配,然后从根节点开始,按照模式图节点的匹配顺序进行匹配即可,匹配方法与MC相同,若除了u″之外,v″的候选集为∅ 时,可以进一步确认影响区域为以v″为祖先的所有节点。当增加的边的类型为CC时,匹配方式与CM相同。
从匹配结果的完整性方面来看,算法将模式图删除non-tree边之后与数据图进行子图匹配得到的匹配结果是原模式图与数据图进行子图匹配得到的匹配结果的超集,其后利用non-tree边的性质将无效的结果从超集里删除,与在模式图中增加边类似[15],这样就保证了匹配结果的完整性。从匹配结果的正确性方面来看,算法采用的是精确的子图模式匹配算法,找到数据图中与模式图满足双射关系的子图,且在剪枝的过程中,仅仅移除无效的节点以及跟该节点相关的边,因此能够保证结果的正确性。
综上,数据图增加边时的处理算法AddEdges的伪代码如算法1所示。
算法1数据图增加边时的处理AddEdges
输入:模式图PT,结果图GT=(VT,ET),match(·),candt(·),插入的边的集合E+,节点匹配顺序order。
输出:新的匹配的结果图GT,更新后的索引match(·)和candt(·)。


算法1首先检查模式图P中是否有与(u,u′)相匹配的边,然后对模式图边的类型进行分类讨论,其中函数character_choice1()用来判断所增加的边是否属于tree边(第1行~第4行)。当对应的模式图的边的类型为tree边时,对(u,u′)的类型进行分类讨论,按照(u,u′)的类型来确定影响区域,相应的在影响区域中进行子图匹配(第5行~第22行)。当对应的模式图的边的类型为non-tree边时,分别判断v、v′所对应的match(v)和match(v′)中是否包含u和u′(第23行~第24行)。对结果图GT进行剪枝(第25行),同时GT可继续用于后续增加边时的匹配计算。
算法2结果图GT的剪枝算法CandVerify()
输入:结果图GT=(VT,ET),模式图P。
输出:匹配的结果图Gr。
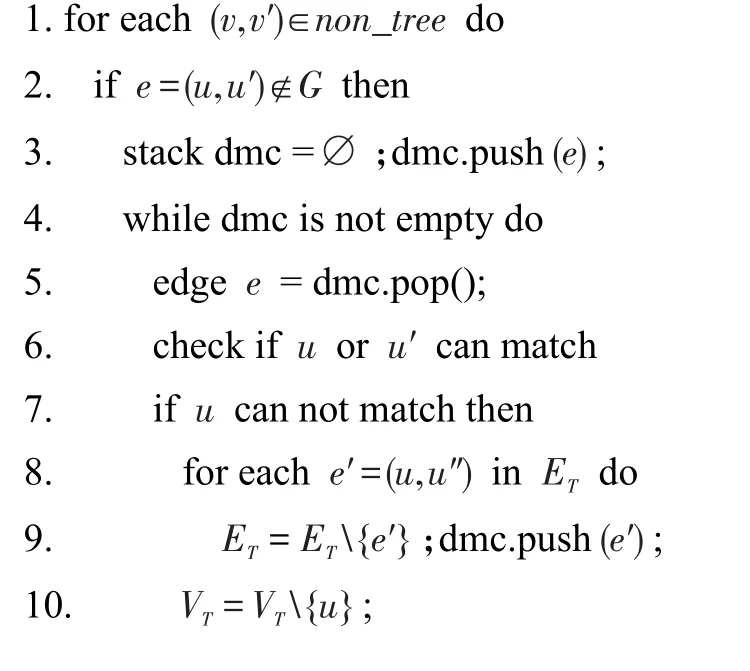
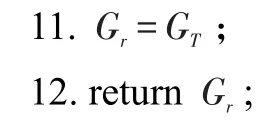
算法2首先检查non_tree边对应的(u,u′)是否满足连接关系,若不满足,将这条边加入到栈中(第1行~第3行)。其次,检查端点的邻节点对应的match(·)中是否有节点和端点满足连接关系,若没有则将GT中端点的邻边及端点删除,并将删除的边加入到栈中(第4行~第11行)。最后返回结果图Gr(第12行)。
以图5为例,图5(a)表示模式图P,图5(b)表示生成树PT,插入边集合包括{(u2,u3),(u8,u4),(u15,u14)}。图5(c)表示增加边(u2,u3)之后的结果图GT1,(u2,u3)为MM边,将边(u2,u3)直接加入到结果图中即可。图5(d)表示数据图增加一条边(u8,u4)后的结果图GT2,(u8,u4)为MC边。此时根据AddEdges算法确定匹配的影响区域为节点v9,需要判断节点v9对应的match(v9)和candt(v9)中是否有与u4相连的节点。由于candt(v10)中u6与u4相连,因此会产生新的匹配结果。然后分别将u4和u6加入到相应的match(v6)、match(v10)中,并将它们分别从candt(v6)和candt(v10)中删除。图5(e)表示数据图增加一条边(u15,u14)之后的结果图,(u15,u14)为CC边,首先从v2开始找到一条到根节点的路径v2、v0。其中v0的候选集为u2且u2∈match(v0),因此可以将u2从候选集中删除,此时v0的候选集为空集,因此可以进一步确认影响区域为v5、v8、v9,并按照v5、v9、v8的匹配顺序找到匹配结果后更新相应的索引。图5(f)表示经过CandVerify()算法剪枝后得到的模式图P的结果图Gr。由于u5与u15不相连,需要将GT3中的相应部分删除。
5 算法复杂度分析
Inc_CFLS算法主要分为三方面,当增加一条边时首先确认模式图的影响区域,之后在新增加边周围的影响区域范围内利用精确子图匹配算法得到匹配的结果图,最后对得到的结果图进行剪枝。
Inc_CFLS 算法使用match(·)和candt(·)作为索引,用来判断增加边的类型,以及判断数据图节点与相应的模式图节点是否匹配。索引match(·)和candt(·)的大小为O(V(P)×V(G))。其中,V(P)表示模式图节点数目,V(G)表示数据图节点数目。当数据图增加一条边后,用E(AFFP)表示模式图对应的影响区域中边的数目,E(AFFG)表示数据图中增加边周围影响区域范围内边的数目。因此,增加一条边需要O(E(AFFP)×E(AFFG))时间来更新结果图GT。当增加完所有的边之后需要利用non-tree边的性质对更新后的结果图GT进行剪枝,得到最终的结果图Gr。若用V(AFFGT)表示GT中的无效的节点,E(AFFGT)表示与GT中无效节点相连的边,则剪枝所花费的时间为O(V(AFFGT)×E(AFFGT))。
IncIsoMatch算法采用模式图的直径作为匹配的影响区域,因此,增加一条边需要消耗的时间为O(E(P)×E(AFFG)),其中E(P)大于E(AFFP)。而且在子图匹配的过程中,Inc_CFLS算法采用查询分解策略进行剪枝,能够推迟冗余笛卡尔积。由此可见,Inc_CFLS算法要优于IncIsoMatch算法。
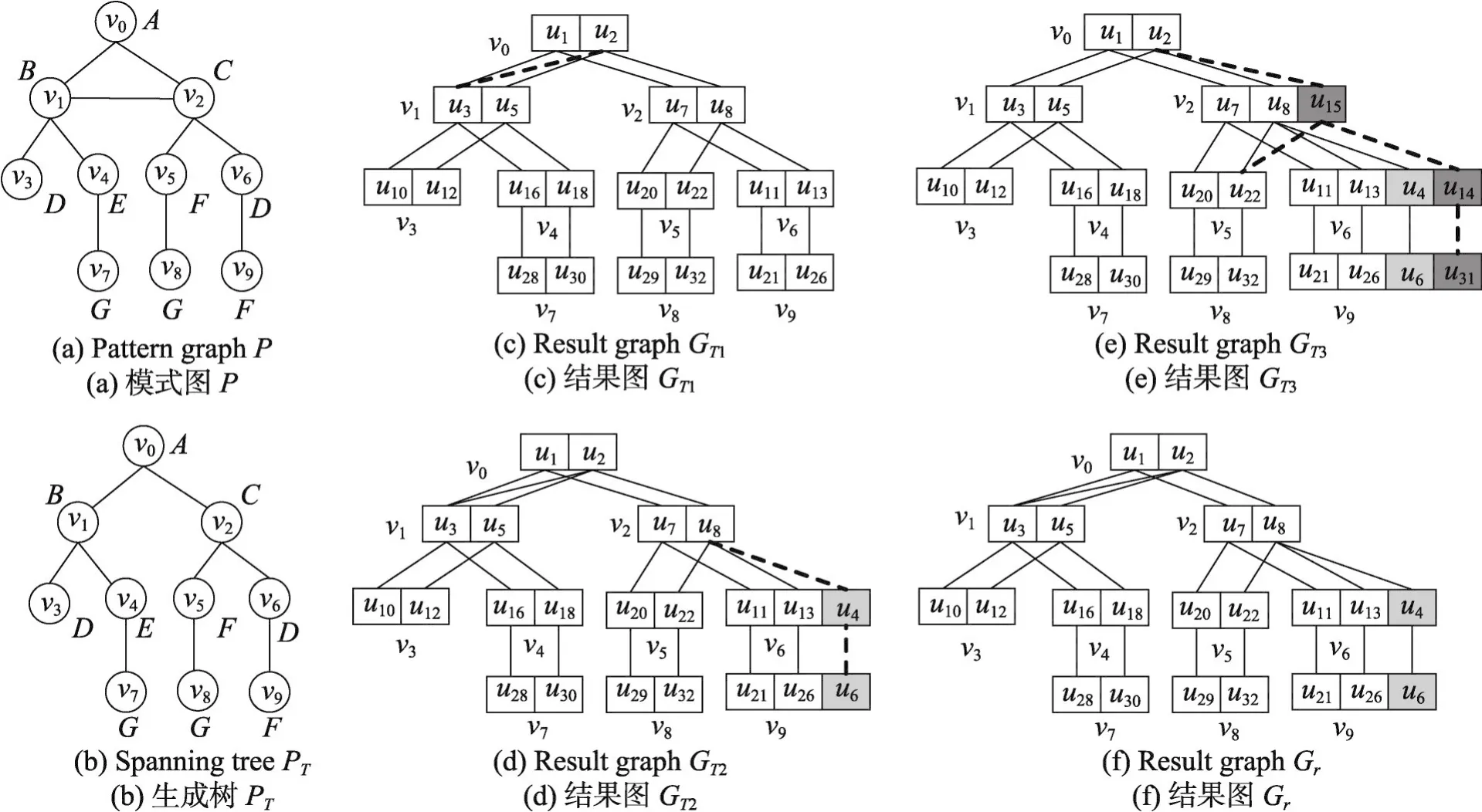
Fig.5 Pattern graph P and its corresponding result graphGr图5 模式图P以及相应的结果图Gr
6 实验与结果
下面对本文提出的Inc_CFLS算法的执行时间进行评估。对Inc_CFLS算法和基于快照的VF2算法[8]以及IncIsoMatch算法进行评估,其中IncIsoMatch算法采用模式图的直径作为匹配的影响区域,并在影响区域内用VF2算法进行子图匹配,比较和分析3种算法的执行时间。由于算法的执行时间和数据图规模、模式图规模以及增加边的数目有关,因此考察了数据图规模、模式图规模及增加边数目发生变化时对Inc_CFLS算法执行时间的影响。
实验使用一台PC设备,配有Linux 64位操作系统,32 GB内存,主频3.50 GHz,所有编程用C++语言实现。实验采用两个真实的蛋白质交互网络数据集HPRD和Human,其中HPRD数据集有37 081条边、9 460个节点。Human数据集有86 282条边、4 674个节点,且Human数据集的节点的平均度是HPRD的4.7倍。模式图采用从数据图中提取的连通子图。通过10次图模式匹配实验,取平均结果作为最终结果。
6.1 模式图规模对Inc_CFLS算法执行时间影响
从HPRD选择35 081条边作为初始数据图,1 000条边作为增加的边集加入到初始数据图中。从Human中选取和HPRD相同规模的边作为初始数据图,1 000条边作为增加的边集加入到数据图中。为了考察模式图规模对算法执行时间的影响,使用3种不同规模的模式图进行实验,分别包括25、50和100个节点。实验结果如图6所示:基于快照的VF2算法执行时间最长,是其他两种增量算法执行时间的10~100倍。当模式图规模相同时,Inc_CFLS算法比IncIsoMatch算法执行时间更短,且这种差距会随着模式图规模的增大而变显著。在Human数据集上IncIsoMatch算法的执行时间明显增加。上述两种实验现象的原因是IncIsoMatch算法把增加边周围模式图直径范围内的区域作为待匹配区域,当模式图规模变大或者数据图密度增加时,IncIsoMatch算法的效率会变差。而Inc_CFLS算法可以迅速地确认受影响区域,将大量无效的中间结果剪枝,因此效率更高。
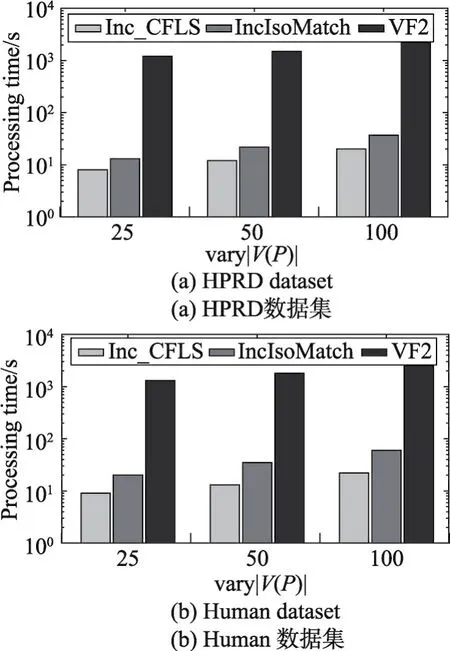
Fig.6 Execution time of different algorithms by varying sizes of pattern graphs图6 不同规模模式图的算法执行时间
6.2 数据图规模对Inc_CFLS算法执行时间影响
为了考察数据图规模对算法执行时间的影响,分别从HPRD选择13 624、24 793、35 081条边作为初始的数据图,1 000条边作为增加的边集加入到初始的数据图中。Human的选择方式与HPRD相同。选取50个节点作为模式图,实验结果如图7所示:Inc_CFLS算法的效率要明显优于另外两种算法,当数据图规模变大时,Inc_CFLS算法和IncIsoMatch算法的执行时间增加,因为数据图规模越大,匹配的候选集也就越多,匹配所花费的时间则会相应增加。对于Human数据集,Inc_CFLS算法的优势更加明显,原因是当数据图规模变大时,会导致数据图的密度也相应增加,IncIsoMatch算法的效率则会降低。
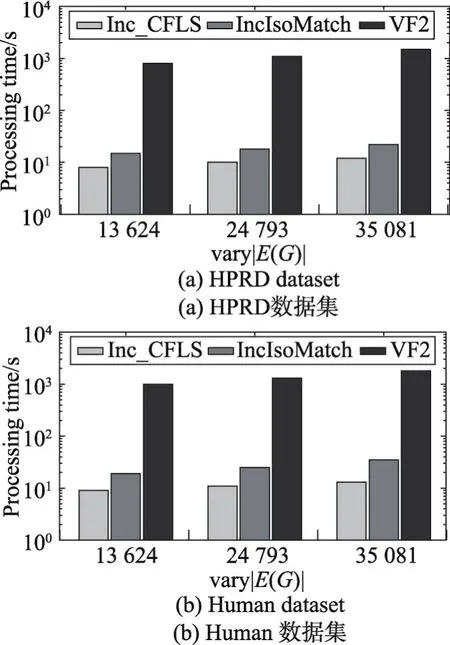
Fig.7 Execution time of different algorithms by varying sizes of data graphs图7 不同规模数据图的算法执行时间
6.3 增加边的数目对Inc_CFLS算法执行时间影响
为了考察增加边的数目对算法执行时间的影响,从HPRD选择35 081条边作为初始的数据图,分别选择500、1 000、1 500、2 000条边作为增加的边集加到初始数据图中。Human的选择方式与HPRD相同。选择50个节点作为模式图,当数据图增加边的数目较多时,使用VF2算法无法进行处理,因此本部分仅对Inc_CFLS算法以及IncIsoMatch算法进行评估。结果如图8所示:随着边的数目增加,算法的执行时间也会增加,且IncIsoMatch算法的执行时间是Inc_CFLS算法的1~2倍。这是因为每增加一条边,IncIsoMatch算法都会把增加边周围模式图直径范围内的区域作为匹配区域,而Inc_CFLS算法能把影响区域进一步缩小,所以随着边的数目增加,Inc_CFLS算法效率提升显著。

Fig.8 Execution time of algorithms by varying the number of inserted edges图8 改变增加边数目时的算法执行时间
7 结束语
本文提出了一种基于结构分解的增量图模式匹配算法Inc_CFLS。该算法不仅能够在模式图匹配的过程中更高效地计算出当前的匹配结果,而且利用增量计算的思想充分利用之前匹配的候选集来降低后续模式匹配中的重复计算。设计实现了面向增边的子算法AddEdges用于增量图模式匹配。选取真实数据集进行实验,结果表明Inc_CFLS算法比目前最好的增量匹配算法在执行效率上平均提升了1~2倍。同时随着数据图或模式图规模的增大,Inc_CFLS算法比目前最好的增量匹配算法在执行时间上的优势会越发显著,展示了处理大图数据的良好可扩展性。

