Pareto支配关系下两阶段进化高维多目标优化算法*

郭晓彤，李玲燕+，朱春阳

1.西安建筑科技大学 管理学院，西安 710055

2.南京航空航天大学 计算机科学与技术学院，南京 211106

1 引言

含有多个目标的最优化问题被称为多目标优化问题，多目标优化问题中当需要被优化的目标数在4个及其以上时被称为高维多目标优化问题，在现实世界中高维多目标优化问题广泛存在，例如工程设计问题、机场调度问题、护士排班问题、车辆控制优化、自来水供应规划等[1]。另外，一些单目标优化问题可以将多个约束转化为优化的目标，变成一个高维多目标无约束的优化问题。例如，文献[2]提出了一个汽车安全性优化设计的问题，具有一个优化目标和多个约束，文献[3]将其一些约束转化为需要优化的目标，将问题转化为具有9个目标的高维多目标优化问题。不同于传统的单目标优化问题和具有2～3个目标的多目标优化问题，这些优化问题的主要特点是需要优化的目标数非常多。

不失一般性，以最小化问题为例，一个具有n个决策变量，m个目标函数的多目标优化问题（multiobjective optimization problems，MOPs）可表述为：

其中，x∈Ω是决策向量；Ω是决策空间；F:Ω→Rm由m个实值目标函数组成，Rm是目标空间，可行目标集被定义为集合{F(x)|x∈Ω}。

使u,v∈Rm，对于任意的i∈{1,2,…,m}，满足ui≤vi，并且在至少一个目标上满足uj＜vj,j∈{1,2,…,m}，称u支配v。给定Rm中的一个集合S，S中的一个解如果被称为非支配解，那就表示在集合S中当没有其他解可以支配它。如果x*∈Ω，在相应的目标集上F(x*)是非支配的。那像x*这样的解组成的集合被称为Pareto最优解集（Pareto solution，PS），相应的F(x*)组成的集合称为Pareto前沿（Pareto front，PF）。

定义1（理想点Z*）

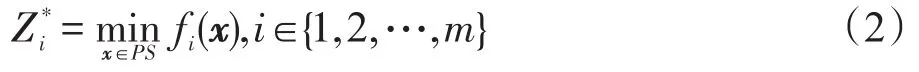
定义2（Pareto极值点B）

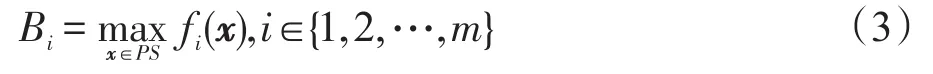
定义3（边界解PCS）对于一个具有m个目标的多目标优化问题，对于Pareto最优解集而言，如果一个解能够满足最小化k个目标(k＜m)，并且最大化其他目标，那么，这样的解被称为边界解。

演化算法作为一个经典的基于种群的启发式算法，能够在一次运行就得到一组解，具有解决多目标优化问题的先天优势。由于这一特性，最近二十年以来多目标演化算法（multi-objective optimization evolutionary algorithm，MOEA）取得了长足的发展[4]。然而，对于目标数量超过3个的高维多目标优化问题（many-objective optimization problems，MaOPs），多目标优化算法的性能往往会急剧下降，因此，高维多目标优化问题近些年受到了广泛关注[5]。

传统多目标优化算法在高维多目标优化问题中存在的困难可以从收敛性和多样性方面总结为以下两点：

（1）选择压力的丢失。选择压力是指种群向真实PF收敛的压力。由于在高维目标空间中，大部分的解互相之间都是非支配的，因此使用解之间的支配关系来选择解的策略将会面临选择压力丢失的困难。图1给出了随着目标数量的增多随机产生的解为非支配的比例，从图中可以看出在目标数量增加时，绝大部分的解都成为非支配的[1]。

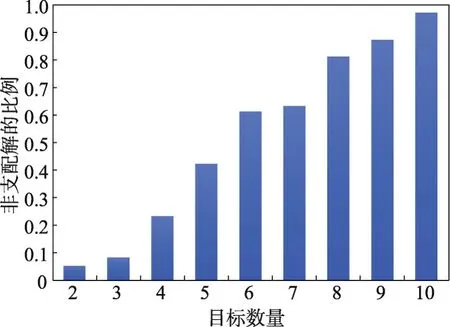
Fig.1 Schematic diagram of nondominant solution in initial solution under different number of objectives图1 不同目标数下初始解中的非支配解比例示意图

（2）多样性保持困难。一般来说，大多数多目标连续优化问题的PF是分段连续的[6-7]，因此不可能得到所有的Pareto最优解。实际的算法设计中通常得到一组均匀分布的具有代表性的解集，以此来模拟PF。当目标数量是2或者3时，问题的PF是一维的曲线或者2维的曲面，保持其多样性较为直观。随着目标空间维度增加，种群中有限个解之间分布较为稀疏，这使得在低维空间中常使用的多样性保持策略在高维多目标优化算法中失效[8-9]，例如在经典的多目标优化算法NSGA-II[10]中使用的拥挤度距离排序。

为了提高传统多目标演化算法在高维多目标优化问题中的性能，学者们提出了大量的改进方法[11-12]。这些方法大体可以分为3类。

第一类方法通过改进支配关系提高算法在高维多目标优化问题上的收敛性能。由于支配关系在高维上将失去选择压力，最直观的改进方法就是修改原有的支配关系以提高收敛性能。这类修改支配关系的方法包括ϵ-支配[13]、L-最优化[14]、混合支配[15]等。文献[16]提出了一种基于格子的高维多目标优化算法GrEA，利用格子支配来改善基于支配算法的收敛性能。

第二类方法是基于分解的方法。这类方法将一个复杂的多目标优化问题分解成为多个单目标优化问题，并分别解决这些单目标问题实现对多目标优化问题的求解[17-18]。这类算法首先生成一组在目标空间均匀分布的参考向量，每个向量对应着一个子问题且每个子问题维护着一个最优解。对每个子问题，通过聚合函数值选择最优解。由于聚合函数值比支配关系对解的选择压力要大，因此基于分解算法的收敛性能往往好于基于支配的算法。此外，此类算法的多样性可以通过其在目标空间均匀生成的一组参考向量得到保持。

第三类方法是基于指标的方法。这类方法通过一个指标值来评价一个解，而不是多个目标值。具有代表性的算法例如IBEA（indicator-based evolutionary algorithm）[19]、SMS-EMOA（SMS-evolutionary multiobjective optimization algorithms）[20]、HypE（hypervolumebased search algorithm）[21]等。

本文组织结构如下：第2章首先对多目标优化问题进行分析，并基于此提出本文算法的设计动机；第3章对基于Pareto支配关系的两阶段进化高维多目标优化算法进行了介绍；第4章对文中使用的基准测试问题集、评价算法性能指标以及相关实验参数的设置细节进行说明，并将改进后的算法与当前领域主流算法在标准测试问题集上进行算法比较实验，并对算法的各个功能模块的有效性进行实验论证；第5章总结全文。

2 多目标优化问题分析

多目标优化问题的复杂性体现在决策空间中不存在唯一的解能使所有的目标同时达到最优，求解多目标优化问题是要找到一组表示目标间权衡关系的Pareto最优解。因此，通常希望能够得到具有以下性质的一组解集。

（1）收敛性：所得到的解集在目标空间上能够尽可能地靠近PF。

（2）多样性：所得到的解集在目标空间上能够尽可能均匀地分布在整个PF上。

对于现存的多目标优化算法，虽然基于支配的算法能够在一定程度上改善基于支配的算法的收敛性能，但由于支配关系先天的劣势，对于目标数量较多的问题（如10个和10个以上目标的优化问题），这类算法的性能仍有待提高。对于基于支配的算法，由于参考向量是在整个目标空间生成，其假设高维多目标优化问题的PF是完整的流形（各个目标之间是完全冲突的）。然而，许多问题特别是实际工程问题的PF是不规则的。例如，DTLZ[22]测试集中的DTLZ5和DTLZ6问题的PF是退化的，其只有两个目标是完全冲突的，在高维上其PF仍然是一个一维的曲线。DTLZ7问题的前沿是不连续的，PF含有2m-1个不连续的部分（m是目标数量）。由于PF的不完整，很多参考向量将不能与PF相交，位于前沿外部的参考向量通常会引导演化算法搜索到位于PF边界上的点，这大大损害了算法的多样性，浪费了计算资源。虽然基于支配的多目标优化算法在一些问题上取得了极好的性能，例如MOEA/DD[23]和NSGA-III[24]在DTLZ1～DTLZ4上均取得了极好的性能，但是这种性能依赖于问题PF的形状，鲁棒性较差[25]。基于指标的算法往往需要耗费大量的时间来计算每个解的指标值，使得这类算法的时间复杂度较高[26]。

基于对现有算法的分析，提出了一种基于Pareto支配关系的两阶段高维多目标优化算法。第一阶段集中计算资源搜索边界解，并通过边界解确定极值点。此后，可以依据极值点将高维的目标空间缩小。在第二阶段可以根据极值点和支配关系共同选择精英解，并通过本文提出的动态最小距离选择多样性较好的解。

支配关系在高维上会丧失选择压力，通过搜索到极值点并缩小目标空间的方式来提高算法的收敛性能，同时发挥了基于支配的算法在多样性保持方面的灵活性。基于分解的多目标优化算法由于需要产生一组均匀分布的参考向量，难以较好地处理具有不规则PF的高维多目标优化问题。本文提出的算法在第二阶段使用了动态最小距离的方法保持解集的多样性，使得算法能够很好地处理PF不规则的高维多目标优化问题。

3 算法设计

3.1 算法总体框架

在本节将介绍提出的基于Pareto支配关系的两阶段进化高维多目标优化算法（MOEA/PT），其中MOEA表示多目标进化算法；P表示Pareto支配关系；T表示two phase。

MOEA/PT由两个子算法构成，在算法开始的第一阶段，通过极值点搜索技术搜索到优化问题的近似极值点，此后算法进入第二阶段，此阶段通过基于Pareto支配关系的进化算法输出一组精英解。值得注意的是，为了提高算法的鲁棒性，第一阶段通过自适应终止条件根据优化问题极值点搜索的难易而自适应终止。接下来的几节将对算法的各个模块进行详细介绍。

3.2 算法的第一阶段及其终止条件

在此阶段，通过极值点搜索算法搜索到优化问题的近似极值点，然后通过极值点缩小算法在高维多目标优化问题的搜索空间。值得注意的是Pareto极值点向量是由Pareto前沿上的各个目标的最大值所组成的，而且极值点只存在于目标空间。因此不能直接在决策空间中搜索，现有的几种极值点搜索算法[27-29]也是通过边界解来间接地搜索优化问题的极值点，本文采用近期研究工作[30]中第一阶段自适应极值点搜索技术来搜索优化问题的极值点。该方法的主要思想是在迭代过程中，通过最小化式（4）找到每个坐标轴上的边界解。

式中，ei代表第i个坐标轴的方向向量；vertdist(F(x),ei)表示F(x)到轴ei的垂直距离。在确定当前种群中的边界点之后，对这些边界点进行变异操作产生新解，并通过帕里托支配关系进行选择。迭代进行以上的操作，直到达到该阶段的终止条件。设所有的边界解所组成的集合为Pb，则可由该集合，根据式（5）近似当前解集P的极值点。

在搜索极值点的过程中，计算每第t代与之前t-200代的边界解最大变化率。由于需要给极值点搜索一定的搜索次数，因此设置检测变化的迭代次数为200，即极值点搜索最少将进行200代1）在搜索极值点的过程中，需要给极值点一定的搜索次数，计算最大变化率的频率过高可能会导致极值点还没有被搜索到就切换到了第二阶段。反之，如果最大变化率的频率过低，会导致算法有可能一直停留在第一阶段从而失去了切换机制的应有的作用。通过在不同的测试问题上的实验表明在整个演化过程中判断5至10次比较合适。在实验阶段，选取的是30万次的函数评估，结合不同目标数时的种群规模，基本上每个目标数的问题都需要迭代1 000多次，在这种情况下，将计算最大变化率的频率统一设定为200代，从而确保每个问题基本上都能进行5～10次的最大变化率判断。。如果由式（6）所得的最大变化率小于预定的阀值0.001，则说明极值点已经在200代之内变化极少，当前阶段继续进行极值点搜索将很难使种群得到更大的改善，因此应终止此阶段，进行下一步的搜索操作。

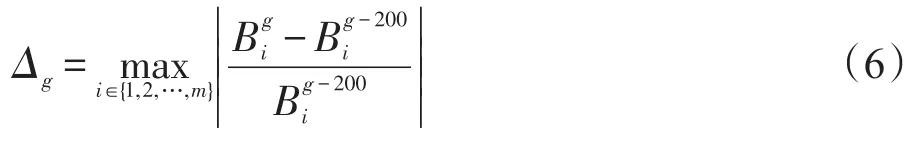
3.3 算法的第二阶段

此阶段中，输入为第一阶段极值点搜索所得的种群，输出是通过基于Pareto支配关系和动态最小距离法的演化算法所得到的一组精英解。关于该阶段的更多细节将在后续详细介绍。

从图2中不难发现，如果边界解确定得不够准确，空间划分选解策略将会出现偏差，如：在PF上的解x1、x近似出的极值点B1是正确的，而x2、x3近似出的极值点B2则由于过小，而导致空间划分出现严重的偏差，导致很多的非支配解也在外部空间被删去。基于此，为了提高算法的鲁棒性以及处理高维多目标优化问题的效率，本文只在混合种群中发现非支配解，如果非支配解的数量大于规定尺寸，基于近似极值点的空间划分选解策略将作为算法选解的一个补充机制，在非支配解中进一步通过空间划分完成选解。

Fig.2 Schematic diagram for nadir point B图2 极值点B的示意图

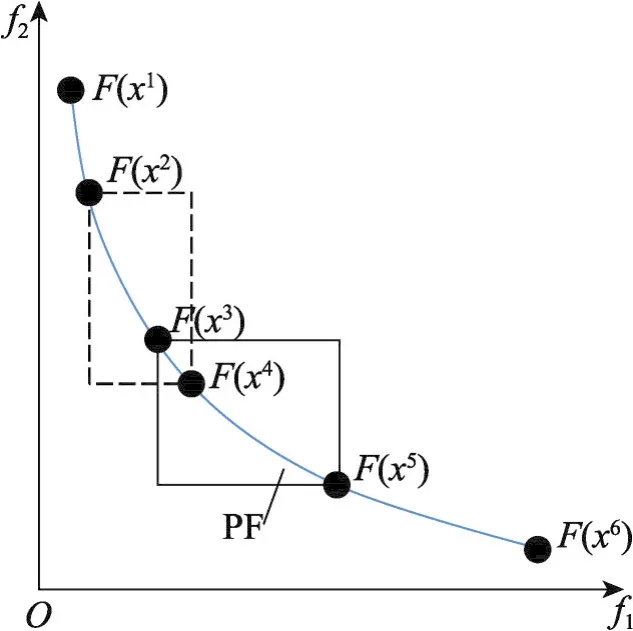
Fig.3 Illustration of diversity maintenance based on dynamic minimum distances图3 动态最小距离多样性保持机制示意图

设当前内部空间的非支配解集为S，其中S为当前内部空间中的非支配个体的数目，若S大于预先设置的种群上限N，需要通过一个准则在S个非支配个体中选择N个个体，并尽量保证保留下来的非支配个体分布的多样性。就多样性保持而言，在算法设计动机部分已经进行了讨论，一次计算的拥挤度距离策略不能很好地考虑每个解对于种群整体的多样性贡献，基于此，本文提出了基于动态最小距离的多样性保持机制，首先将m个边界解保存进精英解集中，然后从剩余的S-m个个体中选择N-m个精英个体。首先计算S-m个解中每个解到其他解的距离，将距离最小的一对解中的任意一解删除，然后重复以上步骤，直至S-N个劣解被删除。如图3所示，以从6个解中选择4个解为例，边界解x1和x6首先被保存下来，然后距离最近的一对x3和x4中的任意一个解被删除。更新每个解的最近解距离，此时，距离最近的一对解为x1和x2，由于x1已经被优先加入到种群中，因此x2将被删除。最终保留下来的解将会是x1、x3、x5和x6或者x1、x4、x5和x6。这与理想的选解方式十分相符。然而，当使用传统的拥挤度距离排序的方式选择解时，拥挤度最小的两个解为x3和x4，因此，x3和x4都将被删除，最终保留下来的解将会是x1、x2、x5和x6，种群的多样性较差。

应用动态最小距离的多样性保持策略，MOEA/PT的第二阶段的算法流程如下。

输入：

（1）第一阶段的极值点搜索算法所保留的种群P。

（2）近似的极值点B。

步骤1生成新解。

从输入种群P中随机选择两个解，然后对这两个解进行模拟二进制交叉（SBX）和多项式变异（polynomial mutation）操作生成新解y，重复以上步骤直至N个新解全部生成，并与父代解组成混合种群Q。

步骤2选择解。

（1）首先将混合种群Q中的非支配解集Q1和支配解集Q2进行分离。

（2）如果|Q1|≤N，Q1将全部保留进P，在Q2中距离理想点Z*欧几里德距离最近的N-|Q1|个解将会保留进P。

（3）如果|Q1|≥N，利用近似的极值点B对目标空间进行空间划分，即x,x∈Q1，如果 ∀i,i∈{1,2,…,m}，满足fi(x)≤Bi，这类解所组成的解集被标记为内部空间解集对于x,x∈Q1，如果 ∃i,i∈{1,2,…,m}，使得fi(x)＞Bi，那这类解所组成的解集被标记为外部空间解集

步骤3终止条件。

如果满足终止代数条件，则终止算法并输出P；否则，返回步骤1。

3.4 MOEA/PT的讨论

高维多目标优化算法中，由于维度灾难，目标空间的大小将随着目标数量呈指数增加。MOEA/PT在第一阶段集中计算资源搜索边界点，虽然在高维空间上Pareto支配的选择压力丧失，但是在边界点的局部空间内，Pareto支配关系仍然具有较强的选择压力，第一阶段使种群快速收敛到PF附近。边界点可以确定极值点，通过极值点可以确定内部目标空间和外部目标空间。内部空间的解被认为是精英解，需要优先选择；外部空间的解由于已经超过了极值点，说明其不在PF附近，将作为补充选择加入到种群中。极值点搜索和划分内部外部空间有效提高了基于支配关系多目标优化算法的收敛性能。

当内部空间的非支配解的数量大于最大种群数量N，则说明此时演化算法已经得到了足够多收敛性较好的解，在第二阶段使用动态最小距离来选择多样性较好的解，由于内部空间已经被初步确定，在使用动态最小距离选择解时，比使用预设参考向量保持解集多样性具有更大的灵活性，因此在具有不规则PF的高维多目标优化算法上将具有较好的性能。

在算法中，快速非支配排序需要O(mN2)的时间复杂度[10]，在动态最小距离法中，计算距离每个解最近的解的距离d需要O(mN2)的时间复杂度，为每个解更新d的值最坏需要O(mN)的时间复杂度，因此，MOEA/PT的最坏时间复杂度为O(mN2)。

4 实验分析

本章在前三节介绍实验所采用的基准测试问题、算法性能度量指标以及算法的参数设置，在后两节将通过两组算法对比实验分别验证算法各个功能模块的有效性以及算法的整体性能。

4.1 基准测试问题

在本文实验中采用目前演化计算领域流行的高维多目标测试问题集DTLZ[16]，该测试问题集是实际工程问题的高度抽象，包含实际工程高维多目标优化问题中多峰、偏倚、退化、不连续等各种特性，能够测试所设计算法的各种性能，且可以根据需求拓展不同的优化目标数，一直是高维多目标优化算法设计所使用的主流测试问题。本文实验中将目标数设置为4、5、6、8。对于决策变量数n，按照文献[14]中n=m+r-1的形式进行设置，其中m∈{4,5,6,8}，对于DTLZ1将r设置为5，对于DTLZ2～DTLZ6将r设置为10，对于DTLZ7将r设置为20。

4.2 性能指标

在本文实验中，实验结果的性能度量指标采用演化计算领域主流的反向迭代距离（inverted generational distance，IGD）[17]。IGD是指计算真实Pareto前沿上的点到求出的近似Pareto前沿的最小距离的平均值。式（7）中P*是真实Pareto前沿，P是算法近似的Pareto前沿，IGD定义为：

其中，dist(v,P)表示v到P中最近点的欧几里德距离。

通过式（7）可以看出，优化算法得到的近似Pareto前沿越接近真实Pareto前沿，并且在整个前沿上分布越均匀，那么计算出的IGD值就会越小。

4.3 比较算法和参数设置

算法对比实验采用领域主流的NSGA-II（a fast and elitist multiobjective genetic algorithm）[4]、GrEA（a grid-based evolutionary algorithm）[16]、NSGA-III（an evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach）[24]和 MOEA/DD（an evolutionary manyobjective optimization algorithm based on dominance and decomposition）[23]算法与本文提出的MOEA/PT算法进行对比。

NSGA-II首先通过非支配排序将待选择的种群分层，随后从第一层开始，依次将每一层所有的解加入到子代种群。当种群数量将要超过事先设定的最大种群数量N时，应用拥挤度距离排序将具有最大拥挤度距离的解加入到种群。该算法是典型的基于支配的多目标优化算法，具有良好的鲁棒性，但在处理高维问题上面临收敛压力丧失等缺点。

GrEA的第一步与NSGA-II相同，首先通过非支配排序将种群分层依次加入自带种群。在最后一层的处理上，GrEA引入了格子支配关系和基于格子的多样性保持策略，以此来提高算法的收敛性和多样性。

NSGA-III同样进行非支配排序。在最后一层的选择上，事先给定了一组参考点，通过将解与参考点绑定，在参考点的局部提高支配关系的效率，同时保持种群的多样性。

MOEA/DD首先利用设定的参考向量将目标空间分成一组子区域。在通过非支配关系确定待选择种群的优先级次序后，通过子区域中所有解的聚合函数值定义区域的拥挤程度和收敛程度。以此决定应该从种群中删除的解以最大化地保持精英种群。

对比算法参数均按照相应的参考文献进行设置。算法在处理不同优化目标数时的种群规模如表1所示。

Table 1 Group size for algorithms表1 对比算法的种群规模

由于不同算法对种群有不同的要求，为了公平对比，在不同的目标上设置不同的种群规模，并在相同的目标上尽可能地采用相近的种群规模，所有算法都将进行30万次函数评估，并独立运行30次。对于MOEA/PT，交叉分布指数和多项式变异分布指数均为20，最大变异概率为0.1（n为决策变量个数）。

本文采用Wilcoxon秩和检验对所得数据进行显著性测试。+和-分别表示在相应测试问题上MOEA/PT显著优于或劣于该算法，如无则表示该算法与MOEA/PT相比无显著性差异，粗体表示在相应测试问题上该算法IGD均值最小。

4.4 MOEA/PT算法各个功能模块的有效性验证

为了验证MOEA/PT算法中极值点搜索技术和基于动态最小距离的多样性保持机制这两个功能模块的有效性，设计了一组算法对比实验，将MOEA/PT算法与传统的快速非支配排序算法（NSGA-II）以及MOEA/PT算法的修改版本MOEA/PT-1算法在8个目标的DTLZ测试问题上进行了对比，其中MOEA/PT-1算法与MOEA/PT算法的唯一区别在于多样性保持策略上仍然采用了传统的拥挤度距离策略。对比结果如表2所示，不难发现MOEA/PT和MOEA/PT-1相对于NSGA-II都取得了较小的IGD值，这说明两种算法都取得了很好的收敛效果，这证明极值点搜索技术对于算法的收敛性是有效的。值得注意的是，相对于MOEA/PT-1算法而言，MOEA/PT算法在所有的测试问题上都取得了最优的IGD值，这说明基于动态最小距离的多样性保持机制能够有效地保持种群整体的多样性。

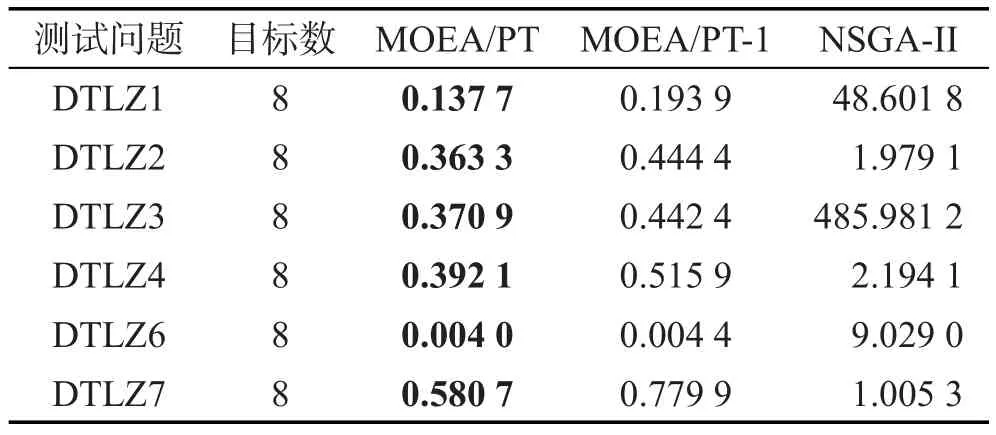
Table 2 Comparison results of algorithms in 8-objectives表2 8个目标的算法对比结果

4.5 MOEA/PT算法整体性能验证

为了验证MOEA/PT算法的整体性能，与3个当前主流的高维多目标优化算法进行比较，这些算法涵盖了基于非支配排序策略、基于格子支配的策略、基于非支配排序和分解混合的策略等。实验结果如表3所示。

通过实验发现MOEA/PT在10个测试问题上取得了最优的IGD值，MOEA/DD在8个测试问题上取得了最优的IGD值，NSGA-III在3个测试问题上取得了最优的IGD值。

MOEA/DD作为一种基于分解框架并引入支配关系的高维多目标优化算法，具有良好的收敛性能。又由于DTLZ1问题的PF是在第一象限的一个完整的超平面，DTLZ2～DTLZ4的PF都是位于第一象限的完整的超球面。MOEA/DD事先设定的一组参考向量位均匀地分布在第一象限的超平面上，与DTLZ1～DTLZ4的PF形状相吻合。因此，MOEA/DD在DTLZ1～DTLZ4上取得了较好的结果。虽然MOEA/PT可以通过极值点搜索和动态最小距离较好地保持种群的收敛性和多样性，但是在DTLZ1～DTLZ4问题上所得解的均匀性不及MOEA/DD。但是在PF形状不规则的问题上，因为MOEA/DD事先设定的参考向量不能够很好地吻合问题的PF，所以MOEA/PT得到了较好的结果。已经说明了DTLZ5、DTLZ6的PF是退化的，DTLZ7的PF是不连续的，MOEA/PT在不同目标数量的这类问题上均取得了最好的IGD值。另外对于DTLZ1～DTLZ4问题，虽然MOEA/PT没有都取得最好的结果，但是其指标值与最好的结果相差较小，这些结果都表明MOEA/PT在不同类型的问题上有更好的鲁棒性。

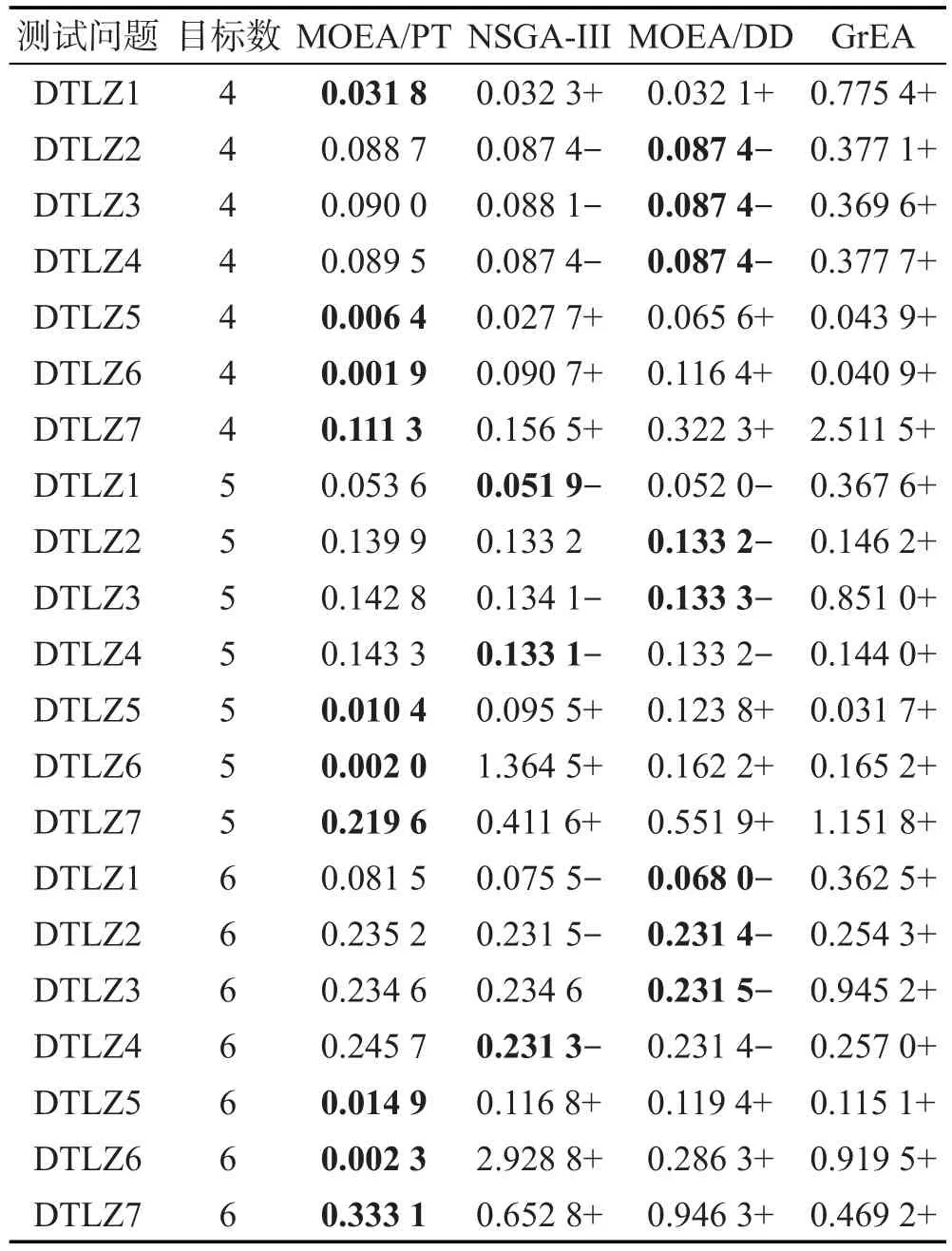
Table 3 Comparison results of algorithms表3 算法对比实验结果

5 结束语

针对现有算法难以较好地解决具有不规则PF的高维多目标优化问题，而实际工程问题中这类问题广泛存在，本文提出了一种基于Pareto支配关系的两阶段进化高维多目标优化算法MOEA/PT。通过第一阶段的极值点搜索技术缩小了目标搜索空间，提升了算法的收敛压力，在算法的第二阶段通过Pareto非支配关系以及动态最小距离的多样性度量策略获得一组在Pareto前沿上均匀分布的精英解。在实验部分，首先通过对比验证了算法各个模块的有效性。然后通过与其他最新高维多目标优化算法的对比，表明了MOEA/PT在PF形状不规则的问题上性能显著优于其他算法，而在PF形状规则的问题上也取得了较好的结果。因此MOEA/PT能够很好地解决PF形状不规则问题的同时具有较好的鲁棒性。在接下来的工作中，将考虑对MOEA/PT进行扩展以探究其在处理房地产领域实际的工程优化问题时的算法性能。