基于贝叶斯网络的桥式起重机故障诊断系统开发

陈志平 林选翔

(杭州电子科技大学 浙江 杭州 310018)

0 引 言

贝叶斯网络是故障诊断中常用推理模型之一。其网络节点由故障事件和各级故障源组成，当某故障事件发生且各层网络节点的先验概率已知，就可根据故障网络模型推测该已发故障的第一故障源。

目前，贝叶斯网络在故障诊断上的应用研究已经取得了诸多进展：郭日红等[1]引入评分函数和蚁群算法对基于贝叶斯的机械模型进行了优化；段荣行等[2]将贝叶斯网络应用于故障树中，降低故障树故障概率推理复杂度；张建功[3]在贝叶斯网络中加入了规则库，应用于起重机故障诊断。但上述研究仍存有不足，主要表现在：① 桥式起重机故障事件的贝叶斯网络模型无法兼顾节点完整性与运用便捷性；② 忽略了贝叶斯网络中根节点先验概率的赋值准确性；③ 仅仅局限在理论上，并不能应用到现实生活中。第一点关系到最终能否得到正确的诊断结果；第二点关系到故障诊断推理的准确度和效率；第三点关系到基于贝叶斯网络的诊断方法能够被广泛应用在工业领域中。

针对上述问题，本文将根据贝叶斯网络诊断算法，构建桥式起重机故障诊断模型，并运用数学手段提高先验概率准确度。最终在Visual Studio平台上开发基于贝叶斯网络的桥式起重机故障诊断系统。该系统能有效地检测第一故障点并给预防性维修提供参考，为基于贝叶斯网络的诊断系统更广泛使用在工业领域中奠定基础。

1 桥式起重机故障诊断模型

1.1 桥式起重机故障分解网络

根据桥式起重机结构特点，结合各零部件失效方式，在咨询相关专家的基础上，将桥式起重机故障按照独立层次主元法分解后构建网络，得到桥式起重机故障分解网络，如图1所示。

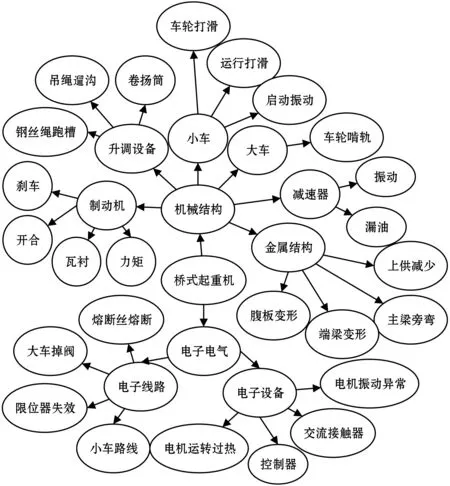
图1 桥式起重机故障分解网络

图1所示的桥式起重机故障分解网络外围节点由故障原因构成，各节点之间的耦合关系由有向线段表达，共涵盖了3个层次共62个节点。

1.2 改进贝叶斯网络诊断模型

利用故障事件解耦形成的贝叶斯网络诊断模型需要使用者熟知桥式起重机的结构划分，在实际应用中存在局限。为此，基于图1所示模型的基础上对贝叶斯网络诊断模型进行改进：在实际诊断案例中提取常见的故障表现作为网络节点加入，存在因果关系的节点间用有向线段连接，跃层或同层节点的因果关系用有向虚线段表示。贝叶斯网络局部诊断模型如图2所示。

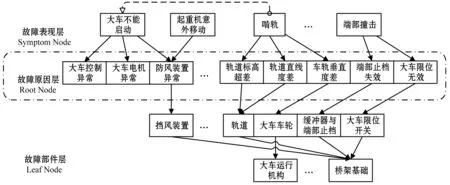
图2 基于贝叶斯网络的诊断模型局部图

故障表现层(Symptom Node)用于描述桥式起重机发生故障时的外部直观表现、故障节点与故障事件的依存关系。相当于将桥式起重机庞大的故障网络模型封装入“黑匣子”，通过故障表现节点与外部联系，并以故障表现节点对贝叶斯网络进行分域推理。

故障原因层是贝叶斯网络中的根节点(Root Node)，故障原因层一方面要与故障表现层建立联系，另一方面又通过与故障部件层关联实现故障诊断网络的整域相关。

故障部件层是贝叶斯网络中的叶节点(Leaf Node)，用来描述桥式起重机发生故障时直接影响到的起重机本体构件，即需要进行维护抢修的零部件。

2 基于贝叶斯网络故障诊断的先验概率评估研究

2.1 基于贝叶斯网络的故障诊断方法

当无法知晓某事物的本质时，可以通过与该事物相关故障事件发生的次数来判断该事物发生的故障概率，这就是贝叶斯公式。贝叶斯公式是概率论中的一种重要概率计算方法，设V1，V2，…，Vk是两两互斥的事件，且先验概率P(Vi)≥0，另有一事件U，它总是与V1，V2，…，Vk之一同时发生，且条件概率P(U|Vi)已知，其后验概率用贝叶斯公式表达如下：

(1)

式(1)提供了一种通过先验概率来计算后验概率的方法，可用于确定故障事件发生的概率。根据贝叶斯理论，不确定性推理就是使用联合概率推理。对于一个包含n个故障原因变量的联合分布P(B1,B2,…,Bn)，利用式(1)可得：

P(B1,B2,…,Bn)=P(B1)P(B2|B1)…

P(Bn|B1…Bn-1)

(2)

而对于任意Bi如果存在π(Bi)⊆{B1,B2,…,Bn}，使得给定π(Bi)，Bi与{B1,B2,…,Bn}中的其他变量条件独立，即P(Bi|B1,B2,…Bn)=∏P(Bi|π(Bi))，则有：

P(B1,B2,…,Bn)=∏P(Bi|π(Bi))

(3)

从式(3)中可以看出，π(Bi)的取值决定了变量Bi的分布。理论上只要确定贝叶斯网络结构中的各节点及其条件概率分布，网络中任何节点的概率都能通过迭代和贝叶斯理论计算得到。

2.2 故障网络模型的先验概率赋值

结合实际运用贝叶斯公式计算出各根节点的先验概率和条件概率，通过类似式(1)的计算可以得到后验概率统计。但在样本有限的情况下，用计算方式所得到的概率直接代替客观先验概率，会影响故障诊断的准确度[4-6]。引入专家意见是一种有效提高诊断准确度的方法。以引起故障部件的故障结点个数为标准，给故障部件划分等级。由于故障节点一般不会超过9个，可将等级划分为9级，其中1级表示最频繁。故障发生概率等级评分表如表1所示，专家根据等级制度对各个故障节点进行评分。

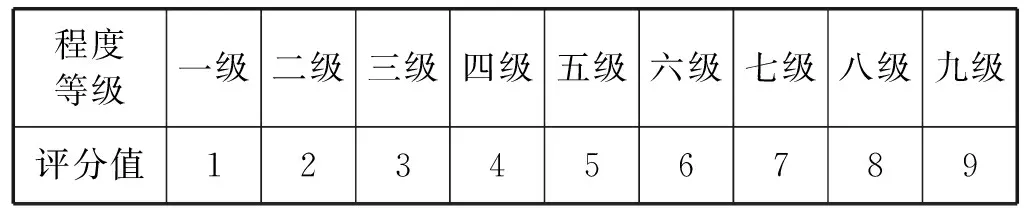
表1 故障发生概率等级对应评分表

每个专家的评价经验不同，所以对同一故障事件给出的评价值也不同，需对每个专家的评价进行综合分析。本文选用格罗布斯准则和肖维勒准则[7]联合评判专家意见，以提高专家评价的可靠性。联合评判法则如表2所示。

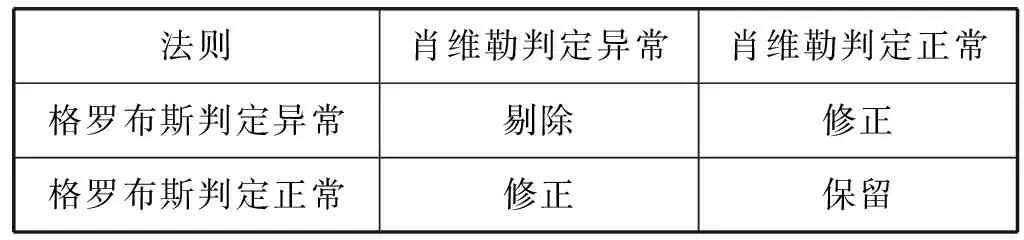
表2 联合评判法则

2.3 专家评价拟合

根据分批估计理论[8-10]，将处理后的专家评价分为两类再进行数据融合。

融合值计算公式如下：

(4)

式中：T(1)、T(2)为分类后每组数据的算术平均值，σ(1)、σ(2)为其所对应的标准差。

初始条件下，各专家可视为等精度评价，首先计算A类不确定度，UA=κρμ，κρ为包含因子，μ为算术平均值的标准偏差。

2.4 引入专家评价的先验概率量化

为了更好地综合专家评价和客观先验概率，需要对两种数据进行关联。以表3所示的桥式起重机制动器故障底事件客观先验概率赋值记录为例进行数据拟合。

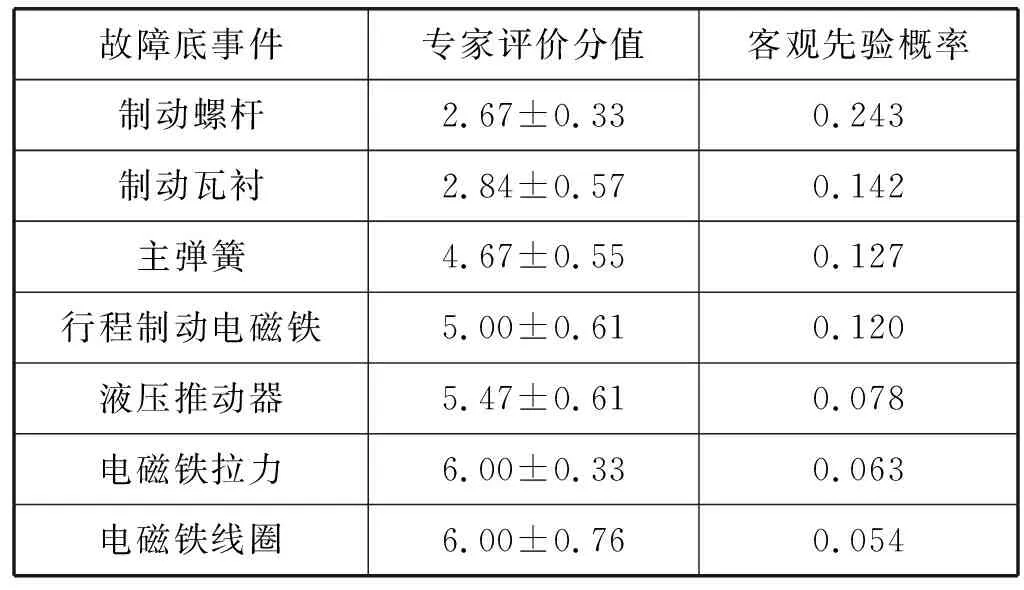
表3 制动器故障底事件先验概率赋值记录表

利用MATLAB中的cftool工具箱进行曲线拟合，对比多种拟合方程，选定幂函数拟合，最终结果如图3所示。

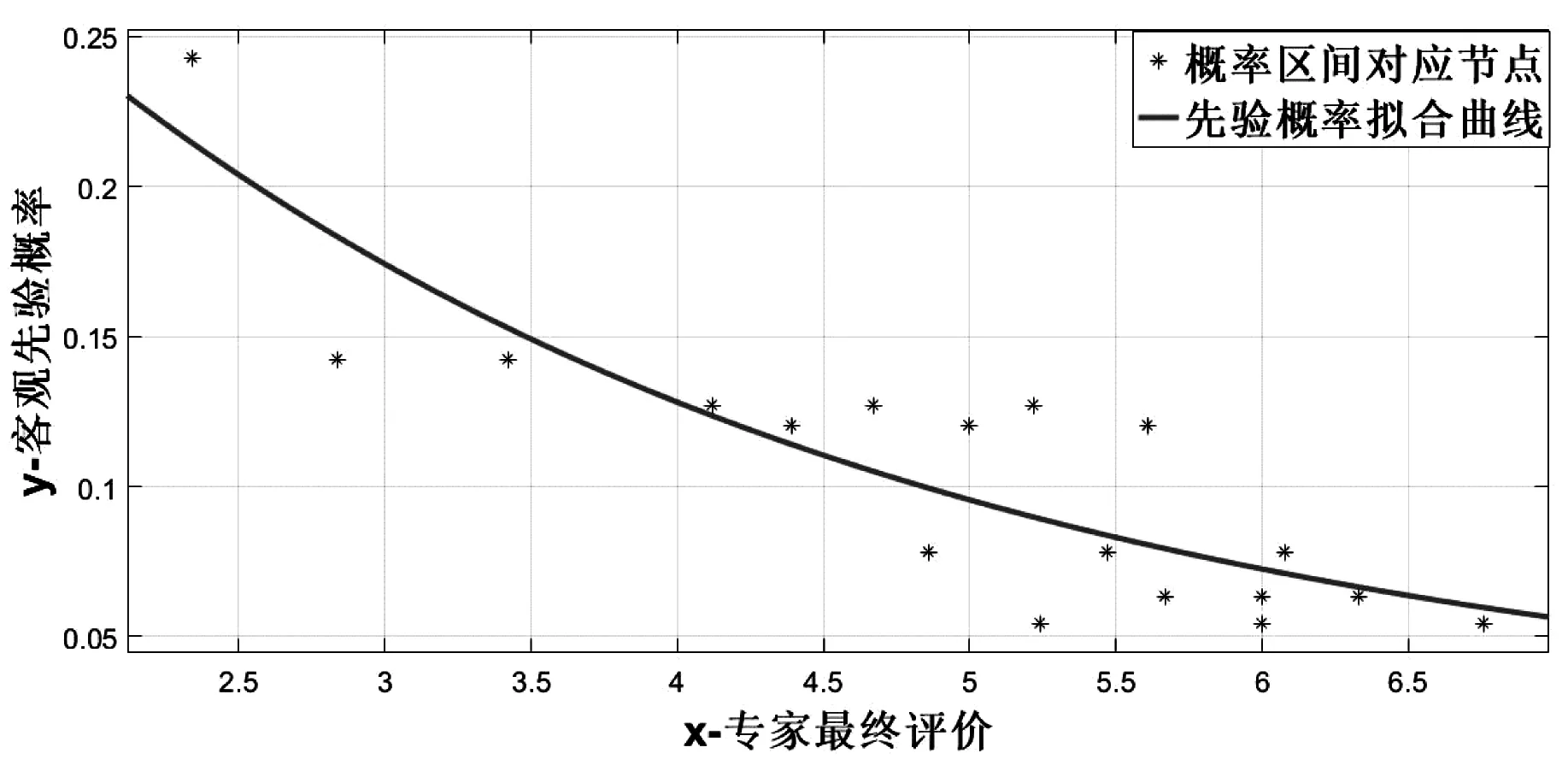
图3 先验概率拟合曲线图

利用拟合曲线，代入各故障底事件的综合评价值，即可得到客观先验概率，结果如表4所示。

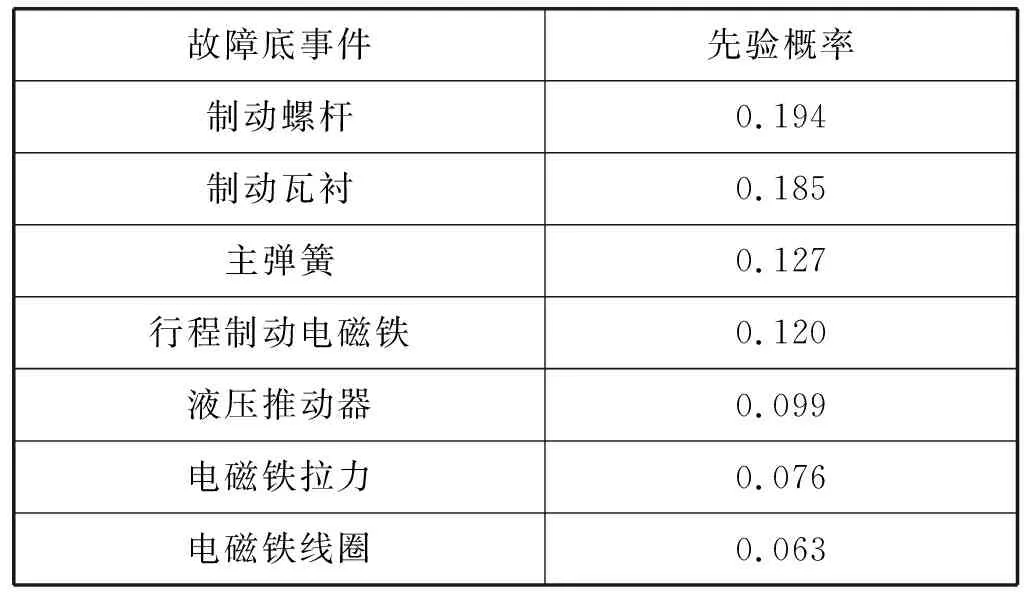
表4 先验概率综合量化概率结果表

由表4可见，最终拟合的先验概率在客观先验概率的基础上融合了专家评价后的结果呈现故障等级越高，概率变化量越小的特点，满足概率故障等级递减规则，也符合实际诊断中对于发生概率极低的一些故障原因较难判定优先级的情况。

3 故障诊断系统开发

基于C#语言和SQL-Server数据库开发了贝叶斯网络故障诊断系统[11-12]，系统分为数据管理模块与功能模块，如图4所示。其中：数据管理模块分别为设备信息、故障记录、数据操作、维护与工具；功能模块分为故障诊断、故障预测。

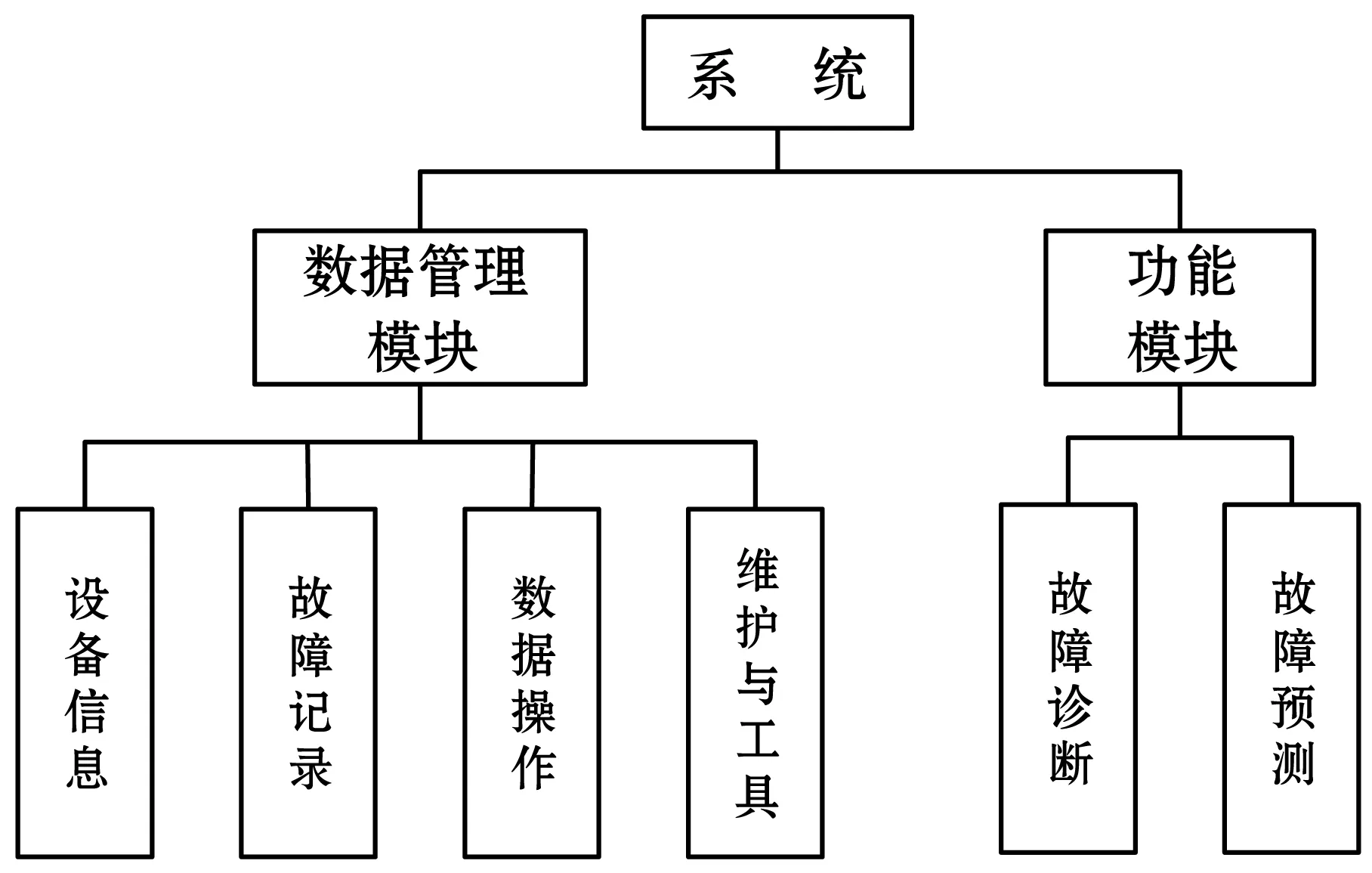
图4 系统功能框架

故障诊断软件封装了基于贝叶斯网络的诊断模型和引入专家评价的先验概率。本文主要讲解故障诊断和故障预测的流程。

如图5所示，在故障诊断过程中，只需输入故障表现(步骤①)，诊断模型便进行贝叶斯网络推理(步骤②)得到故障诊断结果。若诊断结果符合实际，则输出故障表现；若诊断结果不符合实际，则将此结果对应的节点先验概率重置，并更新各节点的条件概率后再次进行贝叶斯网络推理(步骤③)，直到定位第一故障原因。

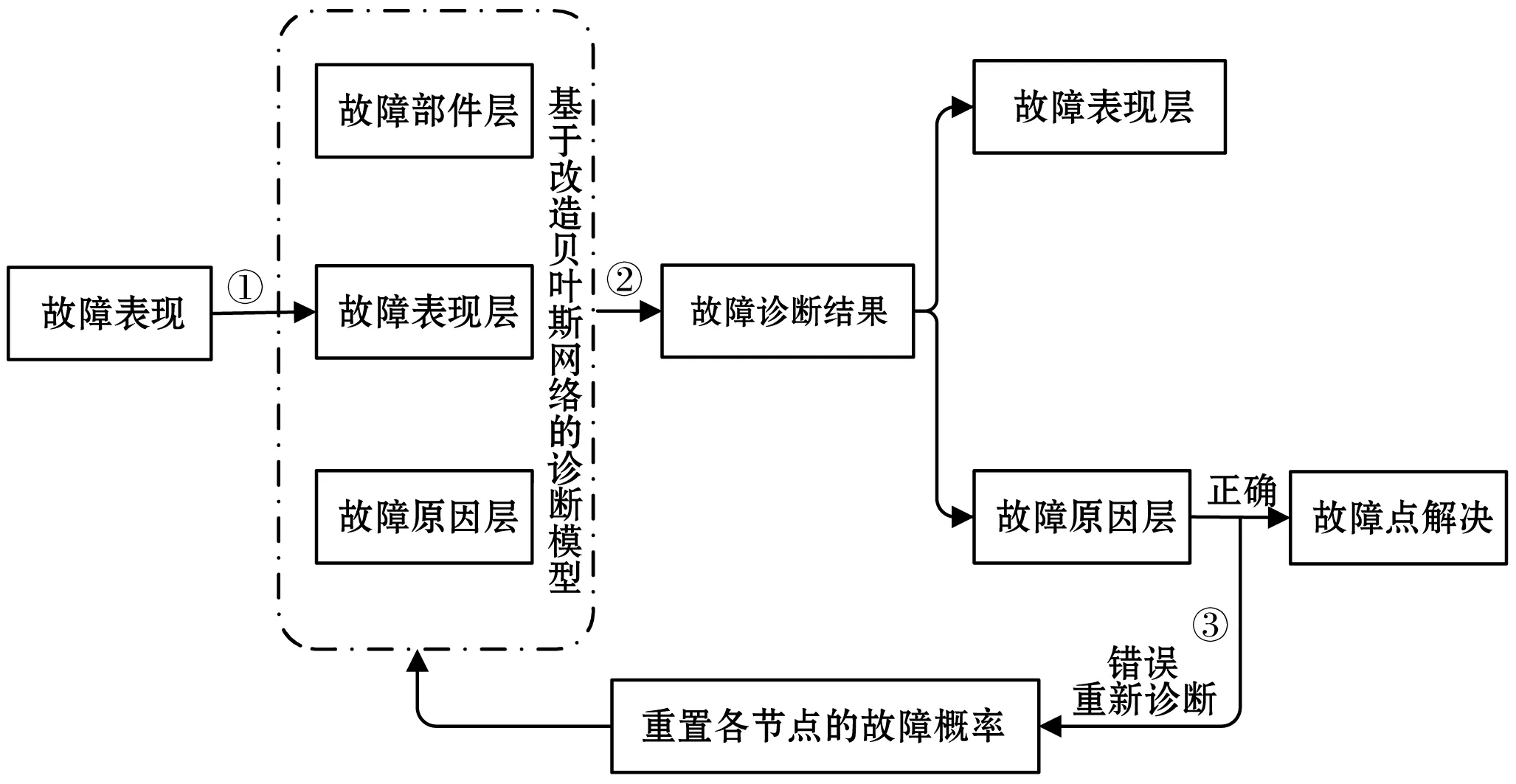
图5 故障诊断流程图

如图6所示，在故障预测过程中，通过PC端串口与桥式起重机实时监控系统的PLC模块通信，监控系统检测到的状态数据经证据输入区(步骤①)后输入贝叶斯网络模型，根据贝叶斯网络推理(步骤②)得到预测诊断结果。若预测结果符合实际，则输出预测的故障表现；若预测结果不符合实际，则增加检测节点个数(步骤③)，将数据重新输入证据输入区再次检测，直至做出最准确的故障预测。

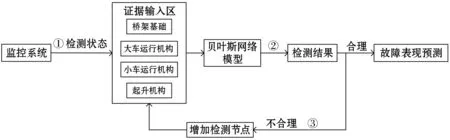
图6 故障预测流程图

4 应用实例分析

为了检验本文提出的基于贝叶斯网络的桥式起重机故障诊断模型诊断效果，选取某港口的通用桥式起重机作为诊断对象，故障描述如下：起重机由持证司机操作，司机打算试空车运行大车行走，大车运行5米左右后，随行人员发现单侧大车电机有冒烟现象，司机立即停止大车运行操作。

运用故障诊断软件的诊断结果记录如下：输入故障表现“大车不能运行或启动”→故障诊断：防风装置无法动作(排除)→继续诊断：大车运行电机异常→提示：啃轨→此时输入故障表现为“啃轨”→故障诊断：车轮垂直度偏差(排除)→继续诊断：轨道直线度不好(准确)。图7、图8为故障诊断界面图。

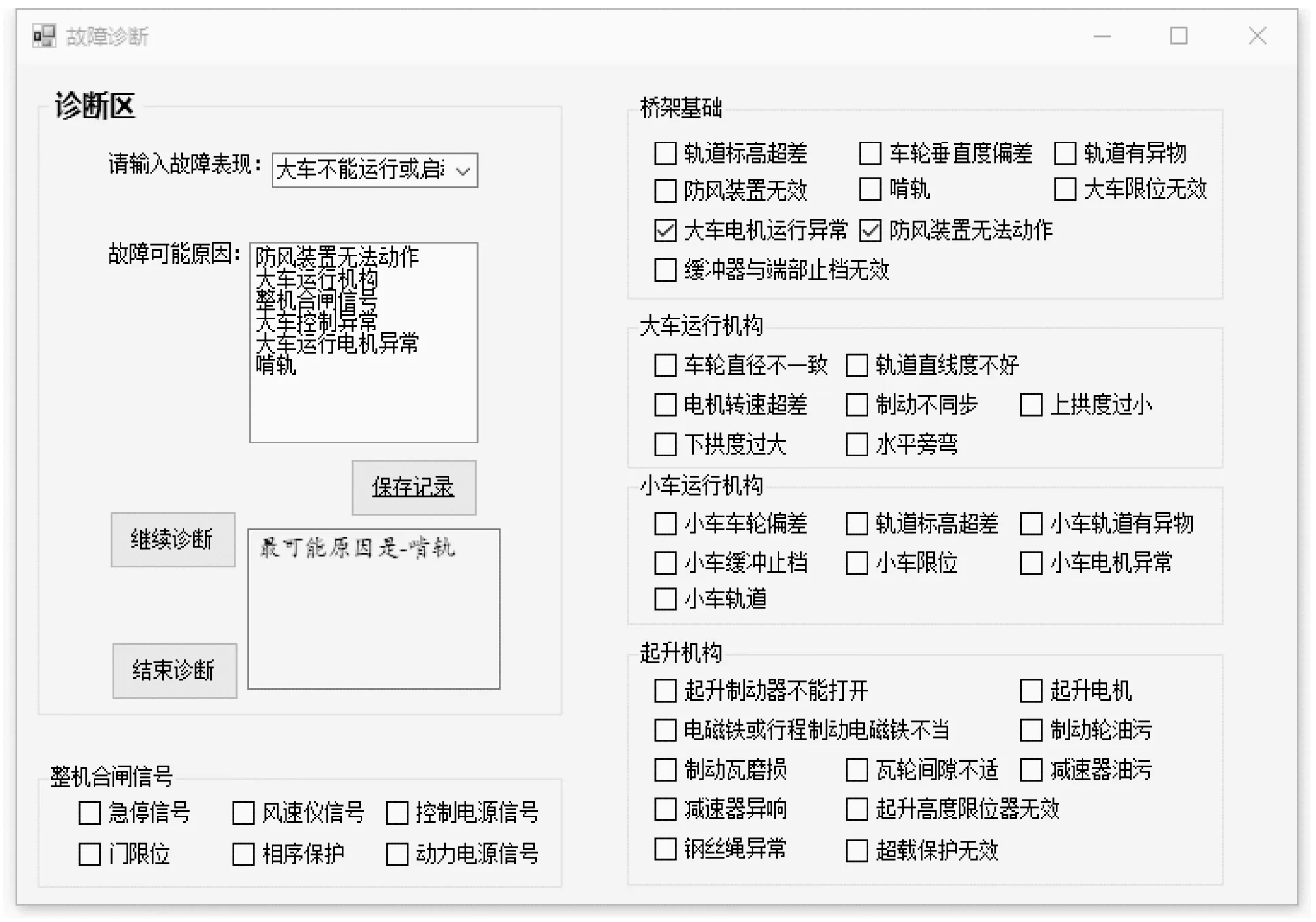
图7 故障诊断界面1

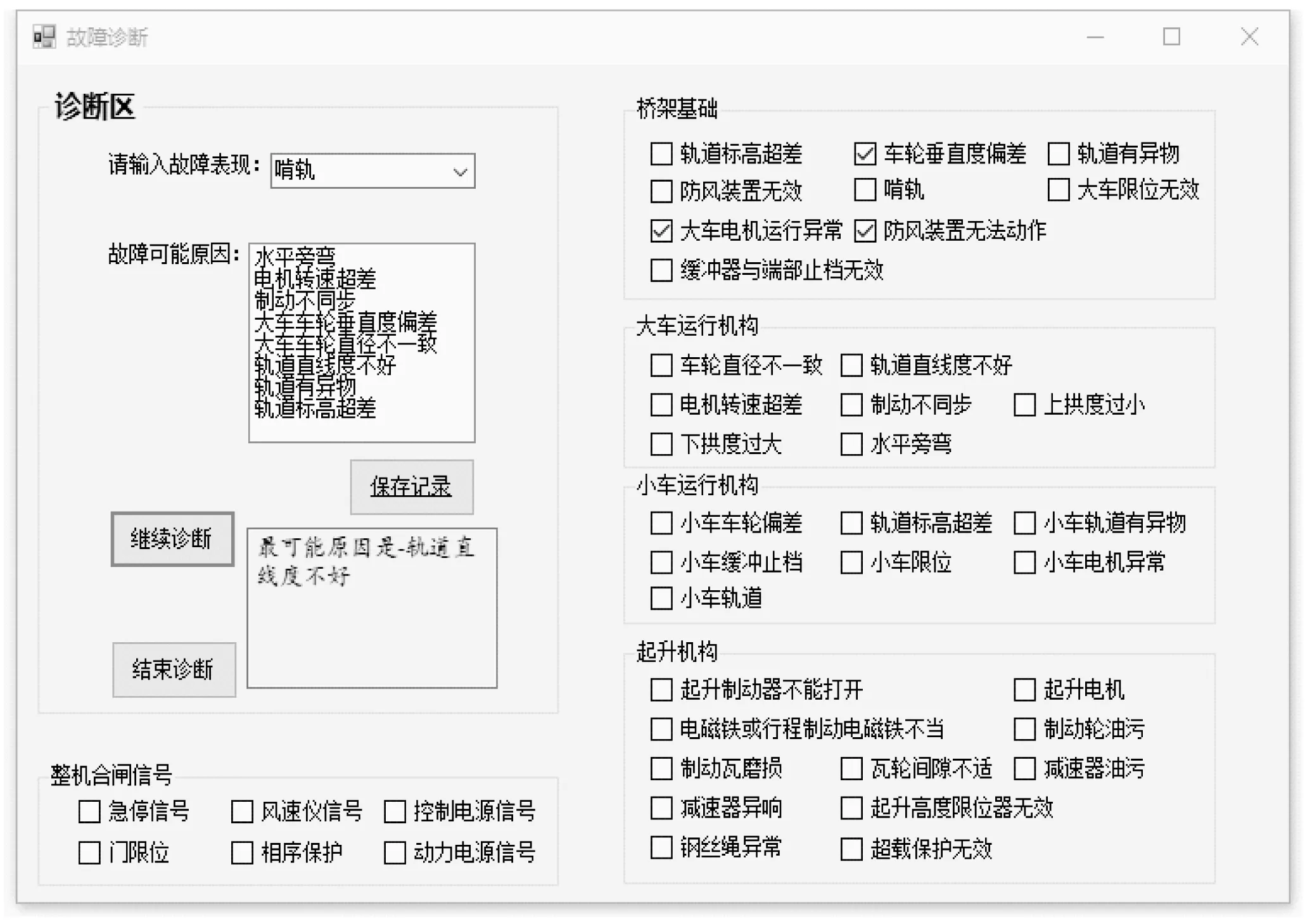
图8 故障诊断界面2

用故障诊断软件推理4次就可定位出故障原因，排查所得到的故障原因为“轨道直线度不好”，符合如图9所示的现场情况。截取“轨道直线度不好”的贝叶斯故障网络模型如图10所示，可知理论上定位故障原因需要排查13次。

图9 轨道直线度不好现场图

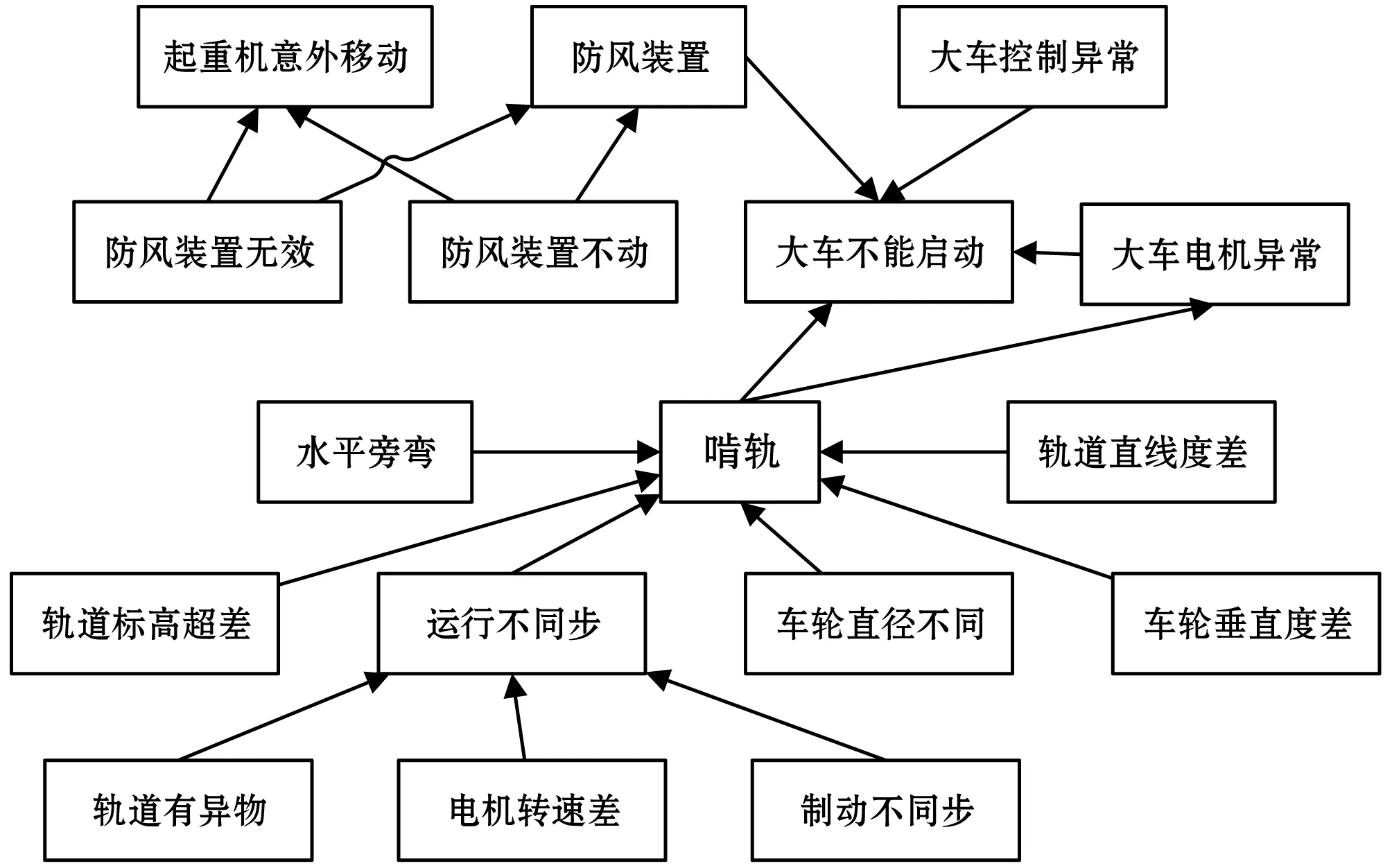
图10 “大车不能启动”的贝叶斯故障网络结构

对其他常见故障表现进行多次现场诊断，记录诊断过程，并与专家诊断过程进行比较，得到诊断效果对比如图11所示。其中X轴表示常见故障表现，Y轴表示定位故障点平均诊断次数。由图11可知，基于贝叶斯网络的故障诊断软件将专家诊断效率提升了37.6%。

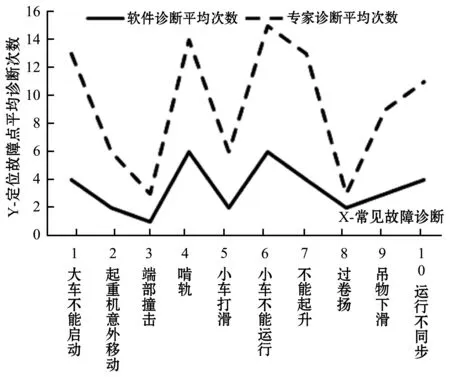
图11 诊断效果对比图

5 结 语

本文构建的贝叶斯网络故障诊断模型兼顾起重机结构模型的全面性与实际应用的便捷性，提出了关于先验概率定量评估的方法，并开发了基于贝叶斯网络的故障诊断系统。此系统验证了故障诊断模型的合理性以及先验概率赋值的准确性，提高了故障诊断和故障预测的效率，推动了贝叶斯理论在大型设备故障诊断领域的广泛应用。