负载对方波激磁位移传感器的影响分析

王科伟，夏 路，王 琳

（1.陆军航空兵驻西安地区军事代表室，陕西 西安 710056；2.中国航空工业集团公司西安飞行自动控制研究所，陕西 西安 710056）

0 引 言

随着多电全电飞机发展，作为飞行控制系统位置反馈的电磁差动变压器式位移传感器（LVDT和RVDT），在高精度测量舵机行程、杆头指令和电磁阀开度等飞行控制领域得到了广泛应用[1]。相比电位计等其他形式的传感器，电磁差动变压器式位移传感器具有结构简单、工艺要求低、无限分辨率、测量精度高、使用寿命长和输入输出隔离等优点[2]。目前，绝大多数的LVDT/RVDT都采用正弦波方式激磁[3]，能够实时、高准确性地将机械位移信号转化为电信号。采用正弦波激磁方式具有抗干扰性能好的优点。

1 问题描述

对于正弦波激磁方式的位移传感器，激磁信号的频率往往被设计得远离系统通频带。采用方波激磁方式位移传感器，一般也遵循同样的设计原则。

为得出正弦波激磁与方波激磁的异同点，本文利用一台飞控计算机采集传感器输出信号，构成闭合回路，并对比试验分析和研究外部负载对传感器输出特性的影响。激磁源为通过信号发生器分别产生的正弦波激磁信号和方波激磁信号。断开飞控计算机与传感器情况下，传感器输出开路，处于空载运行状态；连接飞控计算机和传感器情况下，飞控计算机采集端口相对于传感器为输出负载，传感器处于负载运行状态。

2 传感器原理分析

2.1 传感器基本原理

电磁差动变压器式位移传感器实际上应用的是交流变压器原理，是将非电量的位移变化变换成线圈的互感变化，本身是一种互感式变压器。当变压器的互感量随位移的变化而变化时，输出电压将相应发生变化。在一定的测量范围内，输出电压与位移的对应关系都是线性的。

一般情况下，变压器的负载端为电阻和电容负载；特殊情况下，包括电感负载。

电磁差动变压器式位移传感器由激磁绕组、输出绕组和可以自由移动的铁芯组成。铁芯一端与被测对象连接，当被测对象产生线位移（LVDT）或者角位移（RVDT）时，铁芯也随之运动，从而改变空间磁场分布。

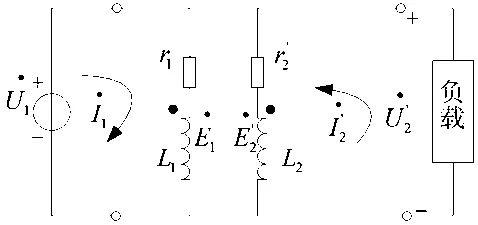
图1 变压器电原理图

当为原边提供交流激磁电压时，副边就会产生感应电动势。随着铁芯的位置不同，副边产生的感应电动势也不同。当铁芯偏离中心位置时，传感器副边有电压输出，且电压大小与位移量成正比。

2.2 负载运行建模分析

为定量计算外部负载对传感器输出特性的影响程度，本文建立传感器与负载交联形成的局部系统的模型，进行传感器的负载运行建模分析。

图2为电磁差动变压器式位移传感器输出端与飞控计算机交联接口的等效模型，ui为传感器空载运行状态下的输出电压，R为飞控计算机运放输入阻抗，C为运放滤波电容、连接电缆分布电容和印制板寄生电容的等效之和，L为传感器副边线圈电感，r为传感器副边电阻，uo为负载测量电压，f为激磁频率。

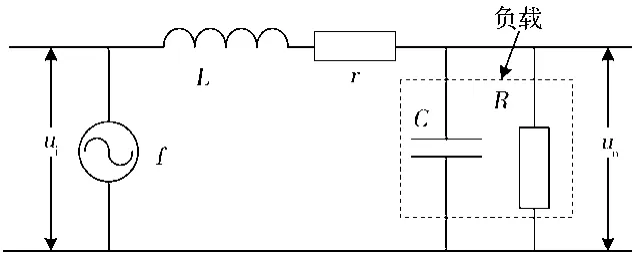
图2 传感器与计算机交联接口模型

由交联接口模型可以计算得到ui与uo关系：

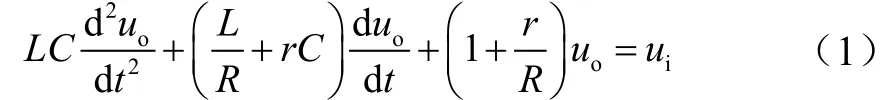
该模型是典型的二阶系统，计算传递函数为：

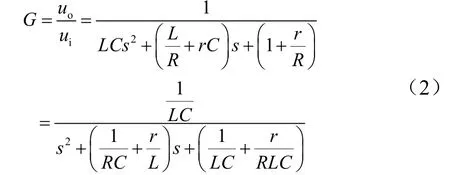
二阶系统的两个特征参数分别为系统的截止频率（带宽）ω和阻尼，于是可计算得到

当传感器参数设计一定即L与r一定时，负载的等效电容C和电阻R对系统的频率和阻尼会产生比较明显的影响，进而直接影响传感器输出信号的动态特性。

本文研究的传感器副边电阻r=40 Ω，副边线圈电感L=30 mH，激磁频率f=2 400 Hz。于是，可以依次计算ω、ξ与负载电阻R、负载电容C的关系。可以得出，系统的截止频率ω随负载电容C增大而减小，而系统的阻尼ξ随负载电容C、负载电阻R的增大而减小。

3 负载对传感器输出信号的影响分析

对于采用方波激磁方式和正弦波激磁方式的位移传感器而言，虽然系统传递函数相同，但是由于二阶系统的输入信号特性不同，所以输出信号也有较大区别。

半个周期内，采用方波激磁方式的传感器空载运行输出信号可以看作是系统的阶跃输入信号，即raquare(t)=1。那么，系统的输出信号为标准二阶系统欠阻尼状态下的阶跃响应信号，时域表达式为：

可知，系统在负载运行时，传感器输出信号受系统频率和阻尼同时影响：

（1）阻尼减小，振荡次数增多，超调增大，调整时间变长；

（2）截止频率减小，上升时间、峰值时间以及调整时间均变长。

本文研究的飞控计算机电阻负载R=1.2 MΩ。考虑分布电容和寄生电容的电容负载C约为100 pF，可以计算得到系统的截止频率ω为574.7 kHz，带宽足够。但是，阻尼ξ仅为0.008 9，无法满足阶跃响应的动态指标要求。所以，传感器输出信号会产生大超调，振荡次数增多，调整时间变长，理论分析结果与试验现象一致。

采用正弦波方式激磁时，传感器空载运行时的输出信号rsin(t)=rsin2 πft作为二阶系统的输入信号。输入信号在s域内的表达式为：

输出信号可以表示为：

进行拉氏反变换并略去小量进行简化处理，可以得到负载端二阶系统欠阻尼状态下的输出响应时域表达式为：

通过理论分析和仿真，得出传感器输出信号主要受系统频率影响：

（1）系统频率如果较低（ω/f＜10），输出信号受影响比较严重，波形失真；

（2）系统频率如果较高（ω/f＞50），输出信号基本不受影响，波形不失真。

在连接相同的飞控计算机负载情况下，系统频率ω=574.7 kHz约为激磁频率f=2 400 Hz的239倍，远大于50。所以，同样条件下，采用正弦波方式激磁时，传感器的输出信号基本不受外部负载影响，信号品质较好，分析结果与试验现象一致。

4 解决措施和试验验证

由以上理论分析可知，对于方波激磁位移传感器而言，传感器与负载交联接口电路形成的二阶系统特征参数对于输出信号的影响非常大。为改善传感器输出信号的品质，可以通过在电路中串联或并联分立元件的方法进行补偿校正，使系统具有期望的频率和阻尼特性，从而获得良好的传感器输出特性。

本文研究的传感器与负载匹配的特征参数中系统频率足够，但是阻尼太小，因此需要补偿阻尼。根据前述内容，可以通过两种方法来补偿系统阻尼：

（1）减小负载电阻R；

（2）减小负载电容C。

本文采用第一种方法，即通过在运放输入端引线之间并联补偿电阻Rc的方法减小负载电阻来补偿阻尼，如图3所示。

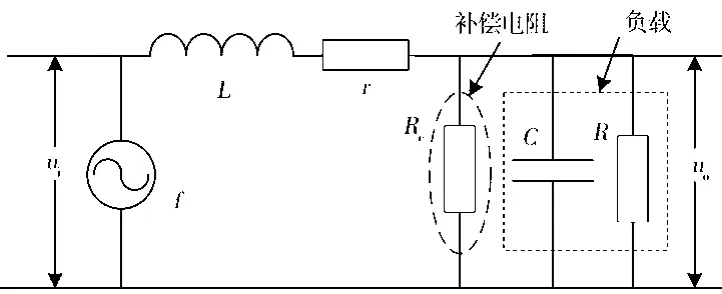
图3 并联补偿电阻后的等效模型

由自动控制基本原理可知，要使二阶系统具有较好的阶跃响应特性，系统的阻尼ξ应在0.7～0.9。根据阻尼计算公式，可以计算得到理想负载电阻值R～在9.5～12.3 kΩ。由于负载电阻R=1.2 MΩ，根据电阻并联公式R～=RRc/(R+Rc)反推，可以计算补偿电阻Rc的阻值区间为9.5～12.3 kΩ。

取补偿电阻Rc=10 kΩ进行试验验证，采用方波激磁方式，传感器固定输出轴，空载运行与负载运行状态下输出信号动态指标对比如表1所示。

表1 输出信号动态指标

试验结果表明，并联补偿电阻之后，系统阻尼增大，系统的动态特性改善明显，传感器输出信号的品质明显提升。

5 结 论

本文分析方波激磁位移传感器受负载影响的原理，比较方波激磁和正弦波激磁传感器输出信号受二阶系统特征参数影响的异同点，给出了通过减小负载电阻或负载电容来补偿阻尼而改善方波激磁传感器输出信号品质的方法。试验结果表明，该方法能够有效消除负载对方波激磁传感器输出信号的影响。