冰载荷和纵倾角对螺旋桨强度的影响

常欣，李鹏，王超，叶礼裕

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

0 引 言

船舶在冰区航行时，冰对船体、推进系统和舵等会产生极大的破坏作用。因螺旋桨裸露在船艉，故其强度问题也成为关注的焦点。相对于常规螺旋桨，冰区航行船舶的螺旋桨导边和叶梢处不可避免地会与冰块发生碰撞［1］，螺旋桨在倒转工况下其随边也会与冰块发生碰撞，可见螺旋桨桨叶的强度是冰区航行船舶一个不可忽视的问题。国内外关于螺旋桨强度的研究很多，钱卫东等［2］使用MSC.Patran软件实现了螺旋桨几何建模和网格划分的自动化，并分析了某冰区航行船舶螺旋桨的强度；Lee［3］依据国际船级社协会（IACS）URI3规范分析评估了水动力载荷和冰载荷下螺旋桨的强度；王建强等［4］针对中国船级社（CCS）规范和IACS URI3规范，对某型螺旋桨进行了CCS Ice Class B3和 IACS PC7冰载荷对比计算；Veitch［5］对冰桨接触下的力进行了研究；刘竹青等［6］利用面元法对螺旋桨强度进行了评估；胡志宽等［1］根据IACS URI3规范，利用ANSYS软件对冰桨碰撞的动力进行了分析，并对碰撞过程中接触力的变化及螺旋桨的动态响应进行了研究。上述研究都是针对某一固定冰级下某单一桨进行的基于规范的强度研究，并未针对IACS URI3规范不同冰级冰载荷下、不同纵倾角度对螺旋桨强度的影响进行相应的研究。

在极地航行、施工和科考的船舶，由于工作时间和区域不同，遭遇的冰的参数也可能不同，即所谓的不同的冰级［7］，从而导致螺旋桨的冰载荷不同，所以进行不同冰级，即不同冰载荷下螺旋桨的强度研究对船舶安全航行具有重要意义。另外，不同纵倾角度的螺旋桨势必会对船舶总体性能带来影响，这就需要针对螺旋桨纵倾角度变化对桨叶强度的影响进行研究。本文拟利用ANSYS软件并结合IACS规范对螺旋桨进行强度计算，分析不同冰级载荷、不同工况以及不同纵倾角对螺旋桨桨叶强度的影响规律。

1 强度计算

本文以公开的极地航行船舶常用螺旋桨R-Class桨为研究对象，材料为镍铝青铜，具体参数如表1所示。本文将依据IACS规范对其进行强度校核，IACS给出的载荷为预期的螺旋桨在寿命期内所能承受的单次出现的最大载荷，并将给出的载荷作为对应的螺旋桨总载荷。根据IACS规范，可计算螺旋桨5个工况对应的冰级下施加的冰载荷值。如表2所示，本文将规范中划分的螺旋桨桨叶5个不同区域当作5个不同工况进行计算，具体工况及施加载荷如图1所示［8-9］。图中，c为对应螺旋半径的剖面弦长。

表1 R-Class桨相关参数Table 1 The parameters of R-Class propeller

表2 不同工况施加的载荷Table 2 Ice loads of different conditions

Ff的计算如下：

式中：Ff为船舶寿命期内桨叶受到的最大向前弯曲载荷；Hice为推进系统设计的冰层厚度；

Fb的计算如下：

式中：Fb为船舶寿命期内桨叶受到的最大向后弯曲载荷；Sice为桨叶冰力的海冰强度指数；

上述计算中，设计冰厚Hice和冰强度指数Sice均为冰级系数，其值如表3所示。

表3 冰级系数Table 3 Index of coefficients for different PCs

1.1 模型建立

在Workbench中建立静力分析工程，利用ICEM模块并结合DM模块，建立4个不同纵倾角度R-Class桨的数值计算模型［10-11］，同时按照图1所示，对螺旋桨桨叶表面进行区域划分，模型划分结果如图2所示。不同纵倾角度R-Class桨5个工况对应的区域面积如表4所示。模型建立之后，在静力计算模块Static Structural中进行网格划分、载荷施加和结果计算。进行有限元分析时，采用结构化网格进行划分耗时又耗力且自动化程度低［12］，为提高计算效率，采用非结构化网格进行划分。

表4 4个纵倾角度螺旋桨对应工况下的面积Table 4 The area of five conditions at different trim angles

1.2 网格不确定度分析

本文的计算由于没有进行实验验证，故在计算过程中需要进行不确定度分析。在进行静力分析的过程中因影响计算结果的只有网格因素，而Workbench中的静力分析在进行有限元分析时具有很好的可信度，所以在进行不确定度分析时只进行网格的收敛性分析。进行网格的收敛性分析至少需要建立3套网格，且3套网格之间需要满足一定的细化率，而本文中采用的是非结构化网格，所以各网格之间的细化率只能近似相等。划分的网格（有限元分析采用的是体网格的划分方式）尺寸分别为0.022，0.03和0.04，3套网格（网格1，网格2，网格3）的网格总数分别为5 143 772，2 030 171和858 468，体网格的细化率分别为2.532和2.365，与文献［13］中提到的 2比较接近，网格如图3所示。

当主要采用的冰级为PC3时，对纵倾角度为0°时的计算工况进行网格收敛性分析。3套网格计算的5种工况下的最大应力值σmax和最大应变值εmax如表5所示。由表可知，网格大小的变化不仅会改变网格的数量，还会引起计算结果的改变，因此需要对由网格变化引起的计算结果的改变进行分析。

表5 3套网格计算的螺旋桨最大应力、应变值Table 5 The maximum stress and strain of propeller blade for three kinds of grid

对于工况1，在3套网格中，每2套网格尺寸变化相邻的网格螺旋桨应力、应变计算结果差值为：

其中，Δε(2-1)表示第2套网格和第1套网格计算结果的差值，同理，Δε(3-2)表示第3套网格和第2套网格计算结果的差值。因此，关于工况1最大应变的网格收敛值则为Rεmax1=Δε(2-1)/Δε(3-2)=0.67 。

同理，可知其他工况的最大应力、应变值的网格 收 敛 值［13］为 ：Rεmax1=0.67，Rεmax2=0.71，Rεmax3=0.85，Rεmax4=0.83，Rεmax5=0.66，Rσmax1=0.57，Rσmax2=0.53，Rσmax3=0.09，Rσmax4=0.82，Rσmax5=0.79。

由文献［13］可知网格的收敛情况有以下4种：

1）单调收敛 0＜RG＜1

2）振荡收敛RG＜0；|RG|＜1

3）单调发散RG＞1

4）振荡发散RG＜0；|RG|＞1

其中，RG代表网格收敛性分析中，针对某变量进行的由网格数量改变引起的差值的比值，在本文中指因网格数量变化造成的最大应力和最大应变变化的比值，即Rεmax和Rσmax。

计算的网格收敛值为 ：0 ＜Rεmax1,Rεmax2,Rεmax3,Rεmax4,Rεmax5＜ 1；0＜Rσmax1,Rσmax2,Rσmax3,Rσmax4,Rσmax5＜1。

3套网格计算的应力、应变云图如图4和图5（图5中，各分图的左图为叶面，右图为叶背）所示。从图中可以看出，3套网格计算的应变、应力云图中极值点的位置、应力和应变的变化趋势基本一致，3套网格的计算结果吻合较好。分析3套网格的计算结果可知：因网格尺寸不同引起的最大应力、应变的差值在1%以内，且应力、应变云图十分相似；从螺旋桨的应力、应变计算结果来看，5种工况下3套网格的收敛值皆在0和1之间，由此可知，3套网格的计算结果均属于单调收敛。综合以上分析，证明了本文计算方法的准确性。在综合考虑计算效率和计算准确度后，采用了网格2的计算结果并对计算结果进行分析。

2 计算结果分析

2.1 冰级对螺旋桨应力、应变的影响

不同冰级下对应5种工况的最大应力、应变值如表6所示，图6和图7为最大应力、应变值的折线图。从图表中可以看出，除工况1和工况2外，各工况下桨叶的最大应力、应变值随冰级的降低而降低；工况1和工况2下的应力、应变值没有明显的改变，在较低的冰级下还有略微增加的趋势；工况3下的应力、应变值虽然随着冰级的降低而降低，但当处于PC7冰级时，桨叶的最大应变值明显有一个反弹。

从PC1～PC7级，冰的存在形态由常年存在于极地水域的多年冰向夏季/秋季存在的薄冰变化，这决定了螺旋桨桨叶载荷的关键因素——设计冰厚Hice和冰强度指数Sice也是从大到小的变化。这导致由规范计算所得的冰载荷从PC1～PC7级是减小的，即5个工况下的冰载荷是不断减小的，所以有上述图表中桨叶应力、应变的变化趋势，亦即螺旋桨的应力、应变值是不断减小的。因此，船舶航行区域的冰级越低，螺旋桨受到的冰载荷越小，对螺旋桨的强度要求也越低。但工况1和工况2下的应力、应变并没有明显的变化，对应的2个工况下施加于桨叶上的冰载荷也就没有太大的变化。这是因为选取的R-Class桨的直径不大于相应冰级下规范对螺旋桨直径的限制，计算选用的冰载荷计算公式中各个参数没有明显的变化，所以计算所得冰载荷也没有明显的变化，由此导致桨叶的最大应力、应变值也没有明显的变化。

2.2 不同工况对螺旋桨应力、应变的影响

图8、图9所示分别为0°纵倾PC1冰级情形下不同工况下的桨叶应力、应变云图。表7示出了0°纵倾PC1冰级情形下不同工况下的桨叶最大应力、应变值。

表6 0°纵倾角时不同冰级下桨叶的最大应力、应变值Table 6 The maximum stress and strain of propeller blade for different PCs with 0 degree trim angle

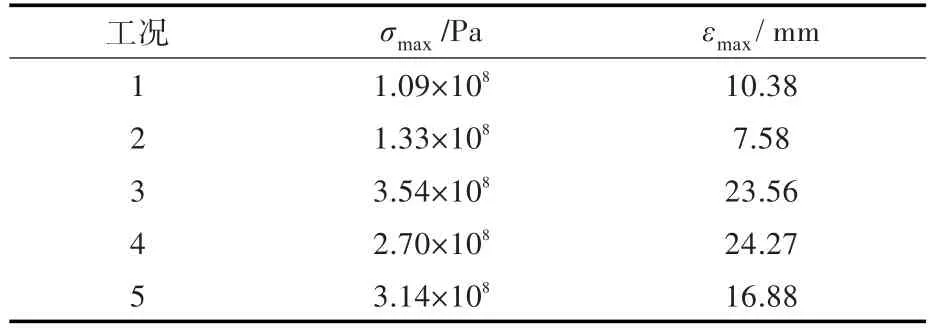
表7 0°纵倾角时不同工况下桨叶最大应力、应变值（PC1冰级）Table 7 The maximum stress and strain of propeller blade with 0 degree trim angle for different conditions（PC1）

从图8和图9（图9中，各分图的左图均为叶面，右图为叶背）中可以看出，工况1和工况4下的应力、应变云图类似，工况2和工况5下的应力、应变云图类似，但工况1与工况4、工况2与工况5施加载荷的大小、施加区域不同，从而导致应力应变方向和大小不同；工况3下的应力、应变云图与其他工况都不同。关于应变：工况1和工况4下的应变最大位置位于叶梢处，且应变以叶梢为圆心大致以环向分布，应变分布较为均匀；工况2和工况5下的应变最大位置位于叶梢附近偏向导边处，且应变的分布基本呈线状分布；工况3下的应变最大位置在叶梢偏向随边附近，桨叶上的应变分布也基本呈线状分布；在这3种情况下，桨叶根部附近的应变均较小（基本为0）。关于应力：工况1和工况4下的应力最大值位于桨叶中部接近叶梢处，且以此为中心呈环状向周围减小扩散，整个桨叶应力的最大值位于叶背；工况2和工况5下的应力最大值位于桨叶叶根处，也是以此为中心呈环状向周围减小扩散，整个桨叶应力的最大值位于叶背；工况3下的应力极值在叶面和叶背处的不同位置，最大值出现在叶面，且该最大值在5个工况中最大，整个叶面和叶背的应力值也未呈现规律性的变化。工况3可对应于倒车时桨叶与冰的相互作用，由于应力规律的复杂性，在该工况下对桨叶的损坏最大，故在冰区倒车时需十分慎重。

R-Class桨的桨叶从叶根到叶梢桨叶厚度逐渐减小；在桨叶不同半径处，桨叶的整体剖面形状呈月牙形翼型。在工况1和工况4下，冰载荷在桨叶的0.9R至叶梢处（如图1中工况1和工况4），施加在该区域的是均布压强，故可以明显看出中部施加的冰载荷应该占比较大，由此导致此处的应变值较大，而叶梢处桨叶因较薄，应变值更大，但由于桨叶从叶梢起是逐渐加厚的，在该区域施加的载荷对叶根处的应变影响变小，所以靠近叶根处的应变值最小，趋近于0。在工况2和工况5下，施加区域如图1（b）和图 1（e）所示，同理，由于施加的是均布压强，所以施加于桨叶中、下部的载荷较大，相对于叶梢，载荷施加的最大位置更靠近叶根处，所以应力的大值出现在叶根处。

2.3 纵倾角度对螺旋桨应力、应变的影响

表8所示为PC3冰级下不同纵倾角度桨叶对应工况的最大应力、应变值，图10和图11所示为表8的折线图表达。当R-Class桨的桨叶纵倾角度在-5°～5°度之间时，5个工况下桨叶最大应变、应力值的变化幅度并不大，但在纵倾角度为10°时，桨叶的最大应变、应力值有一个明显的跳跃增加。这种现象的产生与R-Class桨的三维形状有关，另外，这一规律也与桨叶纵倾角度增加时载荷投影于桨轴方向的力臂有关。由图12可以看出，在工况3下，桨叶的应力、应变规律并没有随纵倾角度的变化而变化，但是应力集中的区域在不断减小，且极值也在不断减小。

由图13和图14可以看出，工况2和工况5导致的应力、应变云图类似的规律并没有随着纵倾角度的变化而变化，工况3导致的最大应力、应变也未随纵倾角度变化。由此可知：5种工况导致的应力、应变的云图规律和趋势并没有改变，但从图10和图11中可以看出，各工况下导致的最大应力、应变值受纵倾角度的影响较大。

表8 不同纵倾角对应工况的桨叶最大应力、应变值（PC3冰级）Table 8 The maximum stress and strain of propeller blade with different trim angles for different conditons（PC3）

3 结 论

本文采用有限元分析方法，系统地计算和分析了冰级条件和螺旋桨桨叶纵倾角度变化等对螺旋桨应力、应变的影响，利用IACS规范强度校核法能较好地模拟极地航行船舶螺旋桨遭受的冰载荷，得出下述相关结论：

1）利用建立的方法对冰区桨R-Class桨进行了系统的计算分析，并对计算网格进行了收敛性分析，验证了本文强度计算方法的准确性。

2）除在工况1和工况2外，从PC1～PC7级，设计冰厚Hice和冰强度指数Sice不断减小，由规范计算所得的不同区域的冰载荷不断减小，相同工况下引起的桨叶的应力、应变值不断减小。

3）由于施加载荷区域的关系，工况1与工况4、工况2与工况5下桨叶的应力、应变云图类似，且并未因冰级和桨叶纵倾角度的变化而变化。

4）螺旋桨桨叶的纵倾角度从-5°～5°，桨叶的应力、应变值没有明显的变化，但是当纵倾角度为10°时，桨叶的应力、应变有一个明显的跳跃，当螺旋桨桨叶的纵倾角度较大时，螺旋桨会产生很大的应力应变，这对螺旋桨的强度十分不利。

本文就IACS规范中对冰区桨R-Class桨的强度校核问题进行了计算分析，得出并分析了不同冰级、不同加载区域和螺旋桨不同纵倾角度对螺旋桨桨叶应力、应变的影响问题，得出了对应的桨叶应力、应变变化规律。但是本文仅对R-class桨进行了强度计算，并在该基础上得出了不同冰级、不同工况和不同纵倾角度对螺旋桨应力、应变的影响，未来仍需对多种型号的冰区螺旋桨进行计算，以对产生该规律的机理进行深入研究。