位移法难点剖析

阙仁波

(厦门大学嘉庚学院土木系 福建漳州 363105)

0 引言

位移法是解超静定结构的一种方法，与力法相比，它在解高次超静定结构和易于程序化方面，比力法更具优势[1-4]，但它在概念上相对较难，而对于很多概念，如独立线位移、铰化法和位移牵连关系等，在很多教材[1-5]和文献[6-11]中的叙述都比较零散，缺乏富有逻辑的串联；或只给“其然”，缺乏对“所以然”的证明；或就题论题，缺乏对“万变不离其宗”之宗的阐释；或结论缺乏普适性，难以应对“常规”之外的题目；或有谬误[7-8]；诸如此类。在结构必须满足的平衡条件、荷载-位移关系和位移协调条件中，难点往往在位移协调条件的建立上。此外，很多难点又与转角位移方程导出时所基于的前提和假设相关。鉴于此，本文拟追根溯源，然后从源点出发，较系统全面地理清理顺位移法的内在逻辑关系，从而破解难点。

1 转角位移方程的导出和位移法的基本思想

位移法是在力法之后基于力法而发展起来的，它所用到的转角位移方程、固端弯矩和固端剪力公式最初都是通过力法推导出来的。对于图1中的3种单跨超静定结构，设AB杆为等截面(等EI)直杆，引起其内力的因素可能是荷载、温变和杆端位移等，现先用力法推导因杆端位移所引起的杆端弯矩和杆端剪力公式[3]。

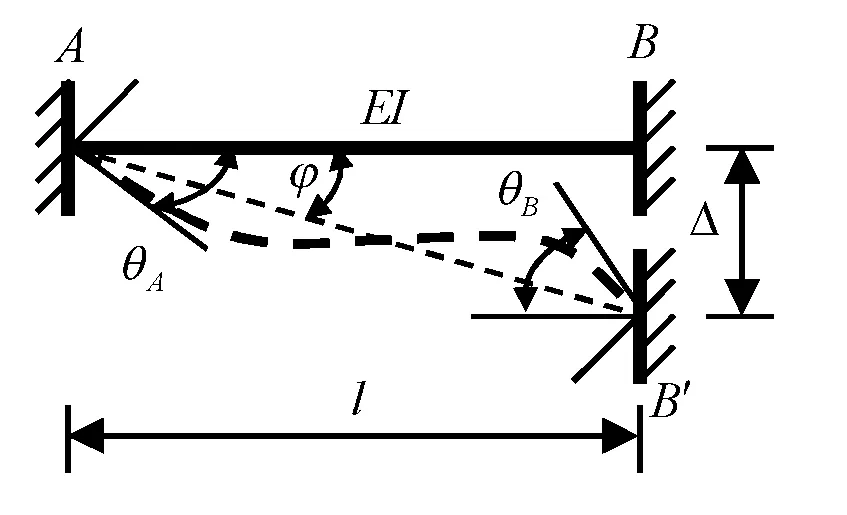
(a)

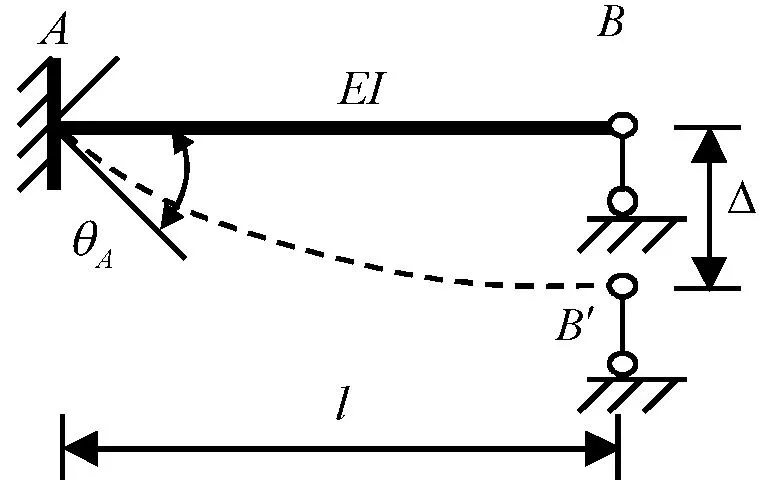
(b)

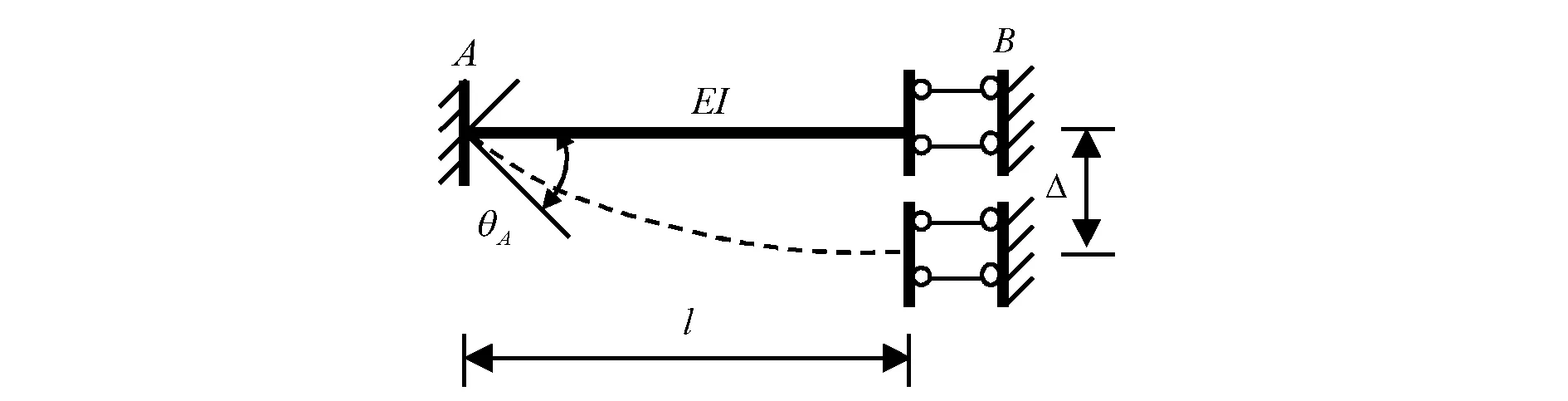
(c)图1 等截面单跨超静定梁

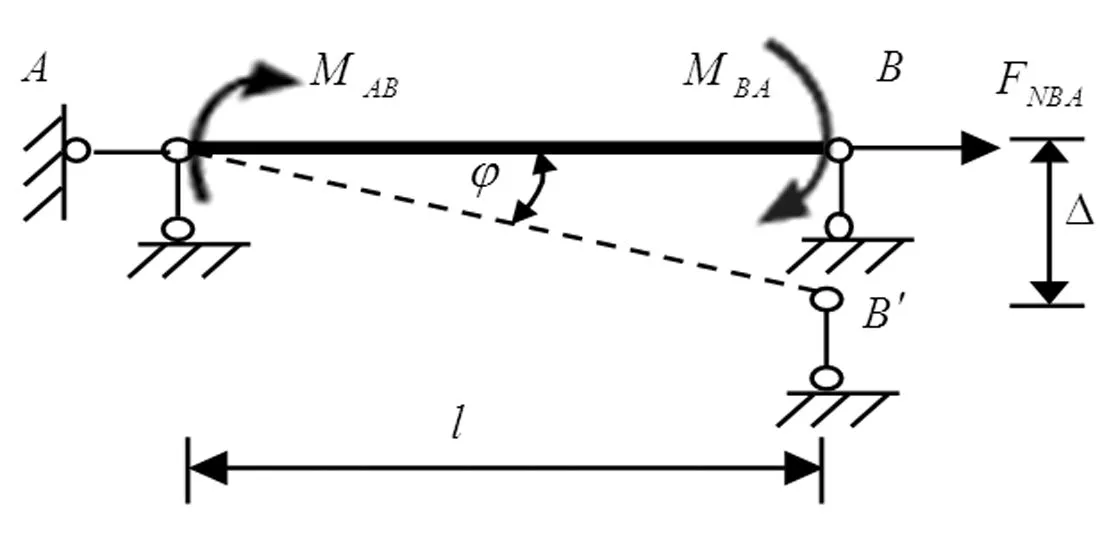
(a)

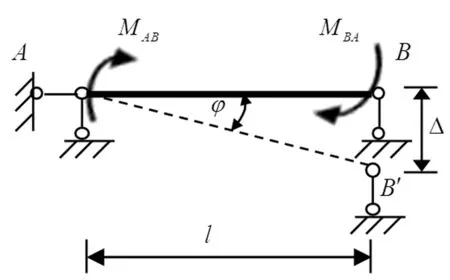
(b)图2 图1(a)的基本体系

图1(a)所示为三次超静定结构，按图2(a)解除多余约束。忽略轴向受压时的P-Δ效应和几何刚度，则FNBA对弯矩和剪力无影响，图2(a)可简化为图2(b)计算；忽略轴向变形，且设弯曲变形是微小的，则可近似取弦长等于原长，弦转角φ=Δ/l(具体原因请见3.1所述)；忽略剪切变形，由图乘法可得：

对于图1(b)，MBA=0(力边界条件)为已知，代入式(1)可得：

可见，θB不独立。

对于图1(c)，FQAB=FQBA=0(力边界条件、剪力静定)和θB=0(位移边界条件、滑动支座)为已知，由式(1)可得：

可见，Δ不独立。

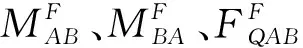
叠加可得总的杆端弯矩和杆端剪力：

式(4)即通过力法推导出来的、作为位移法基础的公式，它是考虑了位移协调条件的荷载-位移关系。位移法的基本体系法即通过附加约束，将原结构解构为一个个如图1所示的3种基本单跨超静定单元和可能存在的静定部分，静定部分只需考虑平衡条件即可确定内力，只对超静定部分应用位移法。通过式(4)求出各单元的杆端弯矩和杆端剪力，再通过重构，求出各个附加约束处的约束力并令其为零(即向原结构等价转化，原结构本无附加约束，故附加约束力应为零)，从而建立平衡方程，求解得基本未知量；进而杆端弯矩，将每一基本单跨解除限制转动的杆端约束，并代以相应的约束力矩(大小和方向与杆端弯矩相同)，即成静定结构，从概念上完成“解超静定”(实际中则可能采用叠加法)。

图2(b)中，未知量有MAB、MBA、FQAB、FQBA、θA、θB和Δ共7个，已建立了4个方程(式(1))，将MAB、MBA、FQAB和FQBA均表示为以θA、θB和Δ为自变量的因变量，一旦后者求出，前者即可求出，故θA、θB和Δ为独立变量，或基本未知量，此处，“基本”即“独立”。按此定义，根据式(2)和式(3)可知，图1(b)的θA和Δ、图1(c)的θA为基本未知量。

2 适用条件和解题要点

式(1)～(4)导出过程中所引入的前提和假设，以及所得出的一些结论，既决定了位移法的适用条件，也提示了位移法的解题要点，具体阐述如下。

2.1 非等截面直杆应在截面突变处分为不同的基本单元

图1中的3种基本单元，杆件均为等截面直杆，故若某直杆不是全长等截面，则截面突变处应按刚结点处理，分杆件为不同的基本单元，如图3所示。

(a) (b) 图3 非等截面直杆梁

2.2 忽略轴力影响对支座性质的影响

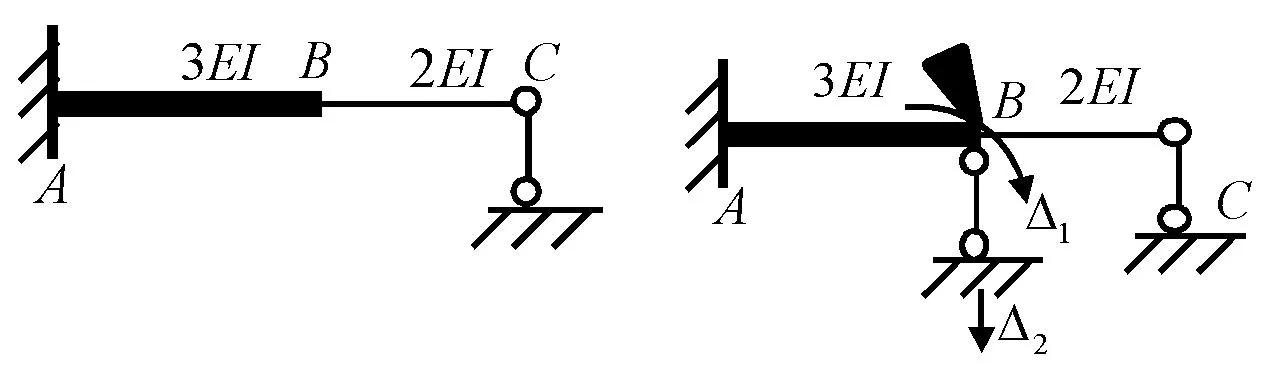
在式(1)～(4)的推导过程中，引入了忽略轴力影响的假定，故图2(a)可简化为图2(b)计算。由此，就求被解构的基本单元的弯矩和剪力而言，图4(a)与图4(b)等效。若已求出A端弯矩，解除A端限制转动的约束，并代以相应的约束力矩，则图4(a)和图4(b)均可按图5所示的简支梁计算，即图6(a)本为一次超静定结构，但若忽略轴力的影响，求弯矩和剪力时可按图6(b)计算，即图6(a)为弯矩和剪力静定、轴力静不定结构。在刚架中，一般先求弯矩，再由对杆端求矩平衡、求杆端剪力，进而由结点投影平衡求轴力，故某单元的轴力还取决于其它单元的剪力或轴力，不能认为图4(a)和图6(a)的轴力为零。

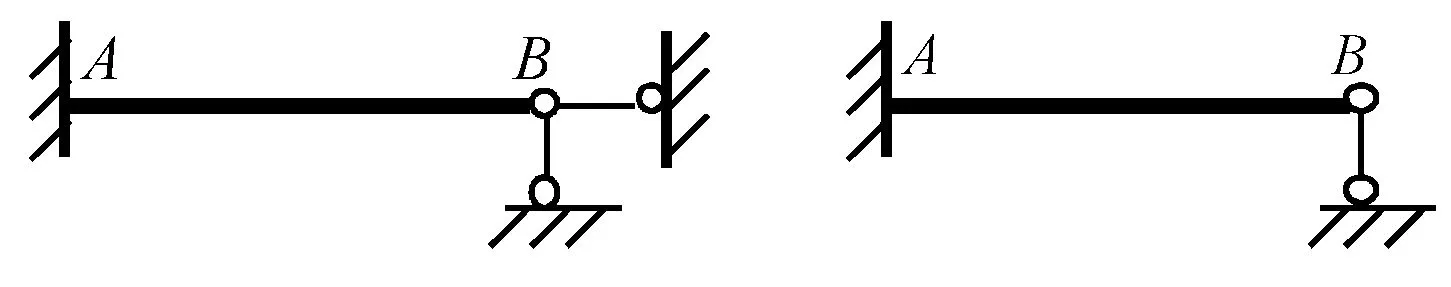
(a) (b) 图4 忽略轴力影响时的等效

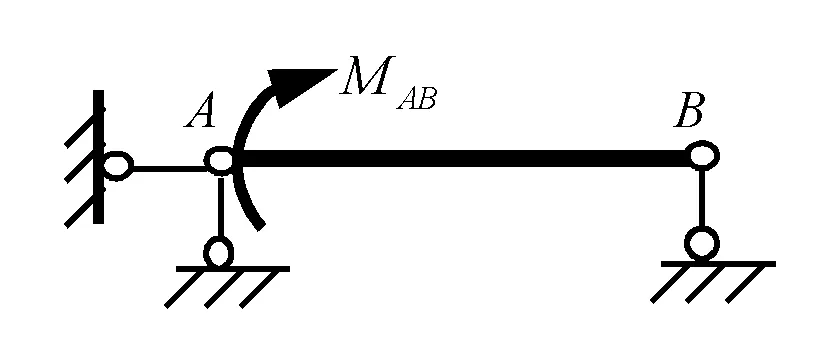
图5 图4的基本体系

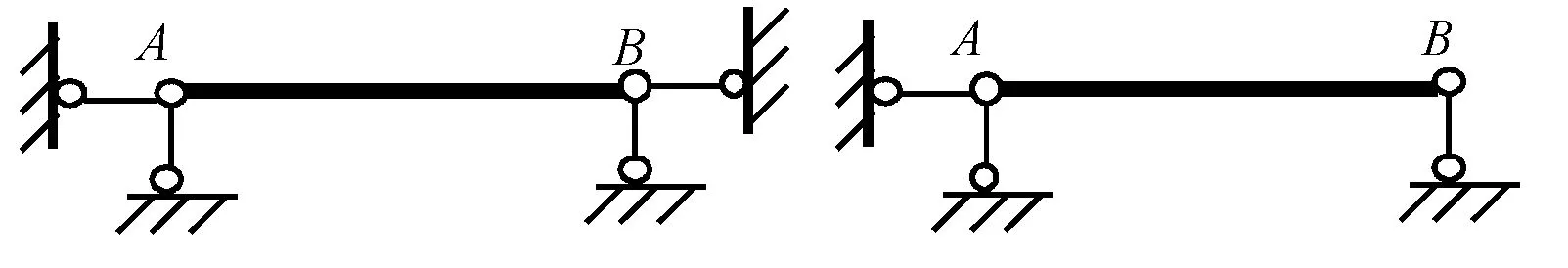
(a) (b) 图6 轴力静不定、弯矩和剪力静定

当忽略轴向变形且只受轴力时，图7(a)～ (c)均可等效为图7(d)，如此可简化分析计算。

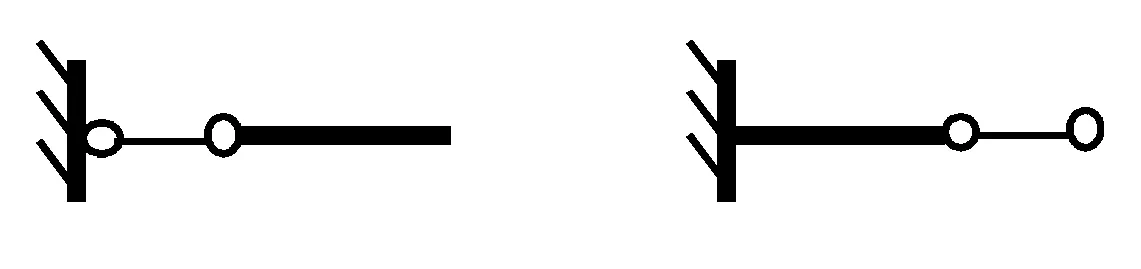
(a) (b)

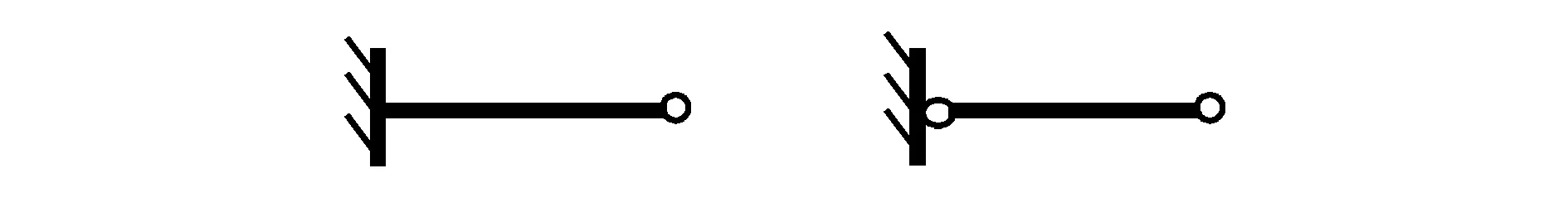
(c) (d) 图7 忽略轴向变形且只受轴力时的等效

2.3 只对超静定部分应用位移法

与力法拆除多余约束形成基本体系相比，位移法是对超静定部分附加约束形成基本体系。因静定部分只需考虑平衡条件即可求解，且支座位移在静定部分不产生内力，故若原结构中有静定部分，可先作如下预处理以简化计算：先根据平衡条件求解静定部分，然后将其去掉，代以其对超静定部分的作用力，只对超静定部分应用位移法(注：矩阵位移法中则同时考虑静定部分，约束住所有结点位移)。但请注意，不要去掉静不定部分。例如，按对图6的分析方法可分析得图8(a)中DF进而FG的弯矩和剪力静定、轴力静不定，而CB则全静定，故可按图8(b)所示按位移法计算，又按图7的分析，可进一步简化为图8(c)，由此得基本体系如图8(d)。

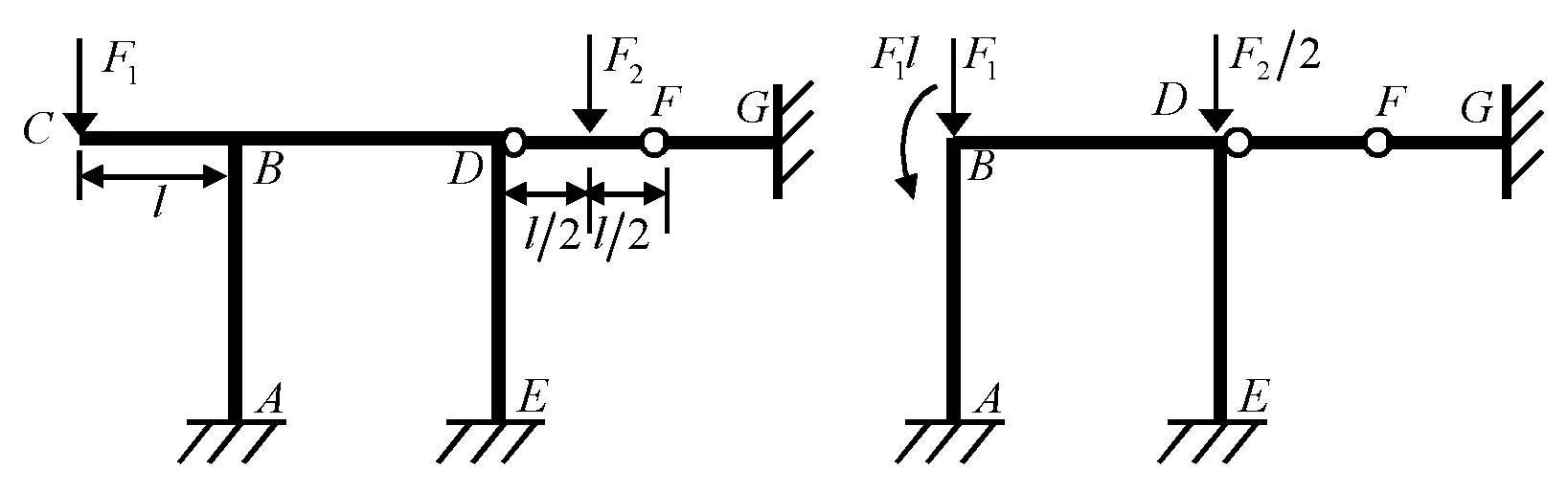
(a) (b)

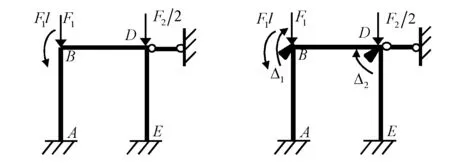
(c) (d) 图8 只对超静定部分应用位移法

3 忽略轴向变形(考虑温变时例外)条件下的位移协调条件分析

3.1 转动

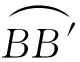
lB‴B=l(1-cosφ)=2lsin2(φ/2)

(5)

lB‴B′=lsinφ

(6)

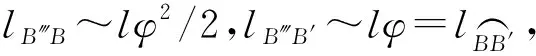
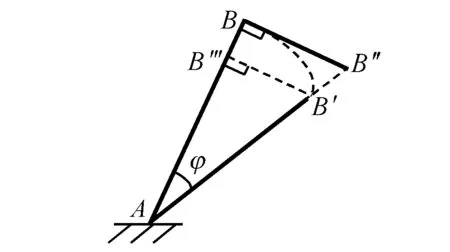
图9 转动时的位移协调条件

例如图10中，若ACBD， 则AC杆和BD杆的C点和D点分别沿垂直于AC和BD，且与原来在同一高度上的直线运动，ΔCA和ΔDB即AC杆和BD杆的侧移。由此可知，CD无侧移，若忽略CD杆的轴向变形，则ΔCA=ΔBD。

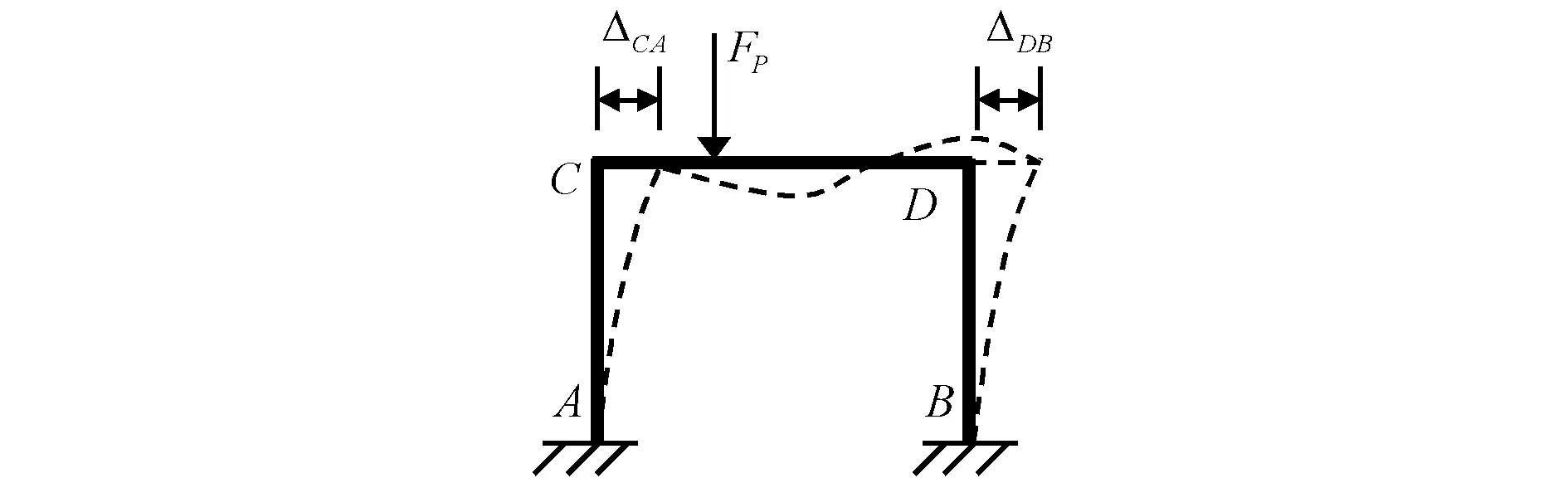
图10 转动时的位移协调条件举例

若一根杆件的两端分别绕与之相连的两根杆件的远端作圆周转动，根据前述可知，可近似以沿切线运动代替沿弧线运动，从而两根杆件(或杆件的延长线)的交点，必为瞬时不动点(否则，该点将有两个不同方向的位移，违反位移的唯一性)。如图11(a)中产生Δ3=1时BC杆的B端、C端和O点(虚交点)，以及图12中产生Δ4=1时BD杆的B端、D端和C点(实交点)。由此，一方面，可建立杆件两端位移之间的牵连关系，如φCB=ΔB/lOB=ΔC/lOC，如图11(a)所示；另一方面，当考虑与侧移相关的平衡时，若截断的各杆(或各杆的延长线)汇交于瞬时不动点，则可对该点求矩，将轴力排除在外，以简化计算，如图11(b)所示[3,4,6,11]。若采用投影平衡，则方程中将含轴力，还得通过结点平衡，先将轴力采用剪力表示出来；对于截断两根以上既不平行也不汇交杆件的情况，要么采用投影平衡，要么采用能量法[11]。

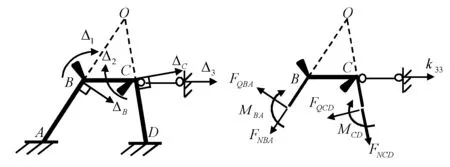
(a) (b)图11 瞬时不动点(虚交点)

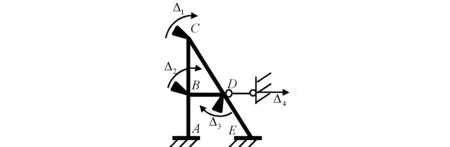
图12 瞬时不动点(实交点)

3.2 平动

图13中，若A、B分别平移到A′和B′，且AA′∥BB′，若忽略轴向变形，假设弦线A′B′与AB等长，则须ΔA=ΔB，AB∥A′B′，AB杆无侧移。

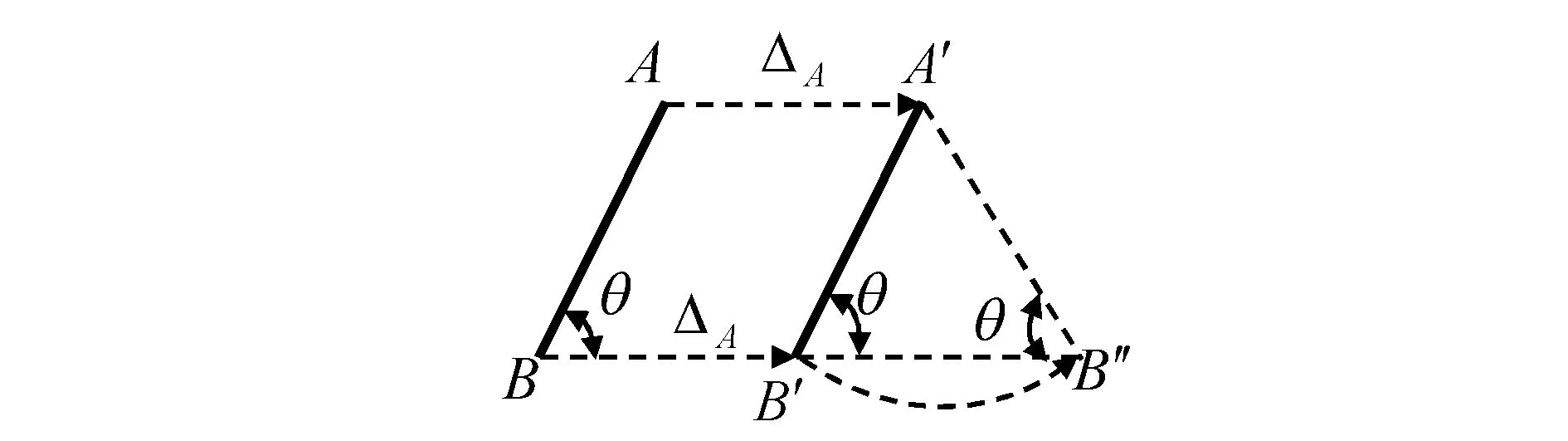
图13 平动时的位移协调条件

例如图14中，按3.1所述，A、B、C三点的位移分别垂直于三根相互平行的柱，故AA′∥BB′∥CC′， 若忽略AB和BC的轴向变形，则由上述结论可得：ΔA=ΔB，ΔB=ΔC，AB杆和BC杆无侧移。

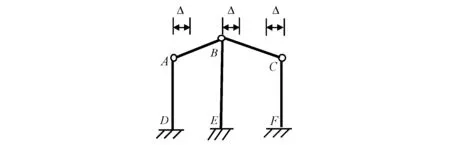
图14 平动时的位移协调条件举例

3.3 平面运动

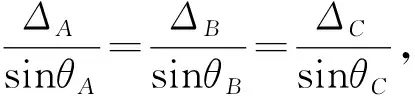
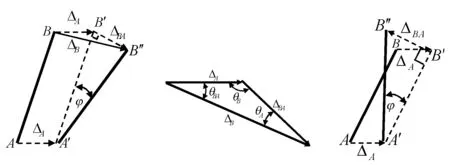
(a) (b) (c) 图15 平面运动时的位移协调条件

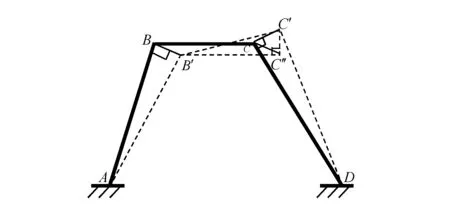
图16 平面运动时的位移协调条件举例1

例如，可采用图17(b)来分析图17(a)中Δ2=1时AB杆的侧移，lAA″=lBB′，A′A″⊥A″B′，由正弦定理从ΔAA′A″中可求得：lBB′=4/3， 侧移lA′A″=5/3。注意，尽管实际中A点不会沿AC竖向移动，但并不影响分析结果。

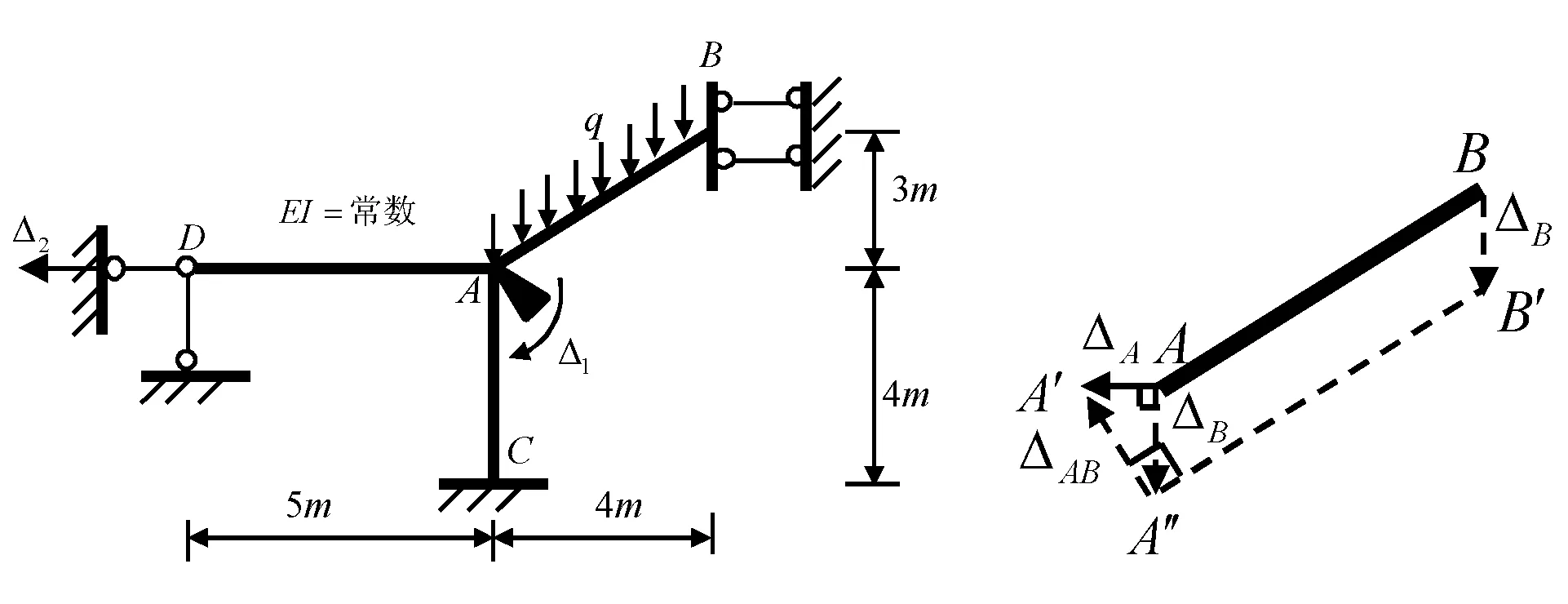
(a) (b)图17 平面运动时的位移协调条件举例2

对图15(a)和(c)，可采用类似图11或图12的方法，设A点和B点分别沿过A点和B点的两根杆件的切线移位，则过A点和B点分别作AA′和BB″的垂线，它们的交点O即为瞬时不动点。根据平面图形绕瞬时不动点转动的转角等于绕任意基点转动的转角的特点，则杆件绕基点A′转动的转角(即弦转角φ)等于绕O点转动的转角，由此可方便地确定弦转角φ[11]以及ΔA和ΔB。

图15中，当BB′与BB″在同一直线上，则必有：ΔBA=0，即AB杆无侧移，且ΔB=ΔA，退化为图13所示的平动。如图10中的CD杆、图14中的AB杆和BC杆。

4 抗弯刚度无穷大时的位移牵连和力矩分配

位移有刚体位移(杆件本身为刚体或杆件作整体同步平移)和变形两种形式，EI→∞的杆件本身不会发生弯曲变形而产生角位移(即变形所致的角位移为0)，若再加上忽略轴向变形的假定，以及同一刚结点处各杆的转角相等的条件，则它的刚体转动或刚体平移将会引起位移牵连，减少基本未知量。

例如，设图18(a)的BCD的EI→∞，则它只会绕C点作刚体转动，一方面，如3.1所述，忽略轴向变形，B点和D点将产生垂直于BD的竖向线位移，导致ΔBA=-lΔ1，因E点无竖向约束，故在D点的带动下，DE将作整体同步平移，不产生内力；另一方面，根据刚结点处各杆的转角相等，可得AB杆的θB=Δ1和DE杆的θD=Δ1。原本的4个基本未知量θB、ΔB、θC和θD减为一个：θC=Δ1。

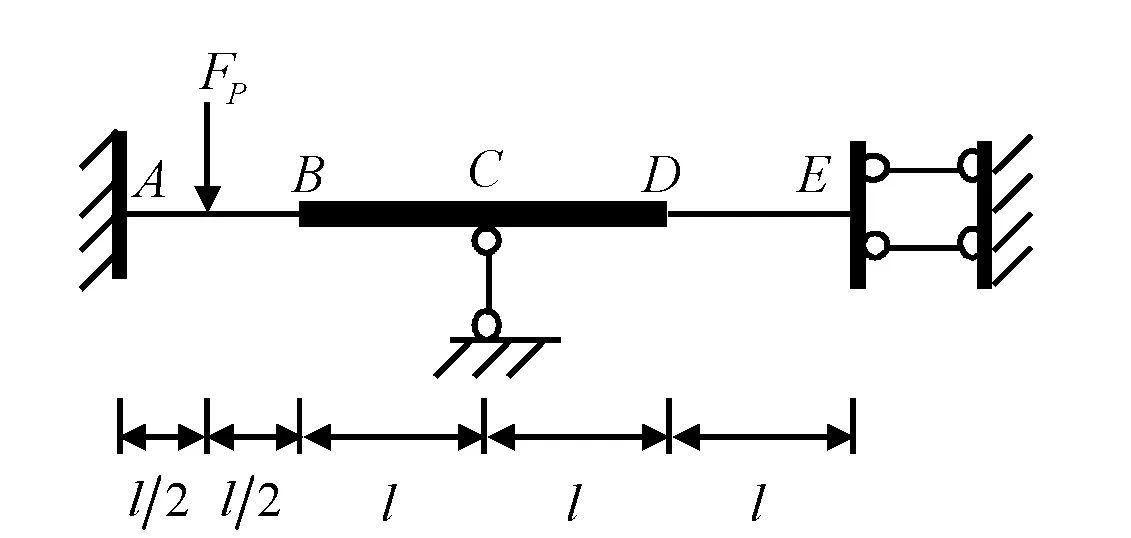
(a)

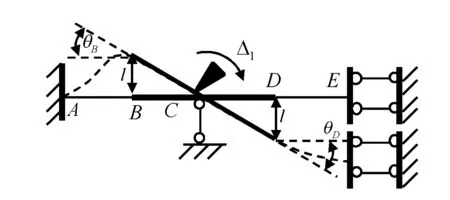
(b)图18 抗弯刚度无穷大时的位移牵连

当EI→∞的杆件的结点作用外力矩时，根据按转动刚度分配力矩的原则可知，该外力矩将全由该杆件承担，其它参与力矩分配的杆件分配所得的力矩为零。附加刚臂的EI→∞，当附加刚臂处作用有外力矩时，外力矩由附加刚臂单独承担，不会在结构内引起内力，由此可快速求出自由项。如图24中，外力矩F1l仅由B点的附加刚臂承受，其它杆件无弯矩，故自由项F1P=F1l，F2P=0。

5 一端固定、一端滑动，且杆轴线与滑动链杆斜交的单跨分析

图1(c)中，杆件轴线与滑动端的链杆平行，故沿杆件切向的剪力静定。若不平行(图19(a))，则剪力不静定(图19(b))，若将支座反力沿轴向、切向和转向分解(图19(c))，则从限制轴向线位移、切向线位移和转角3个自由度的角度来看，图19(a)与图1(a)一样可看作是两端固定的(图19(d))，但跨长沿杆轴长，θB=0，Δ可按式(10)计算。

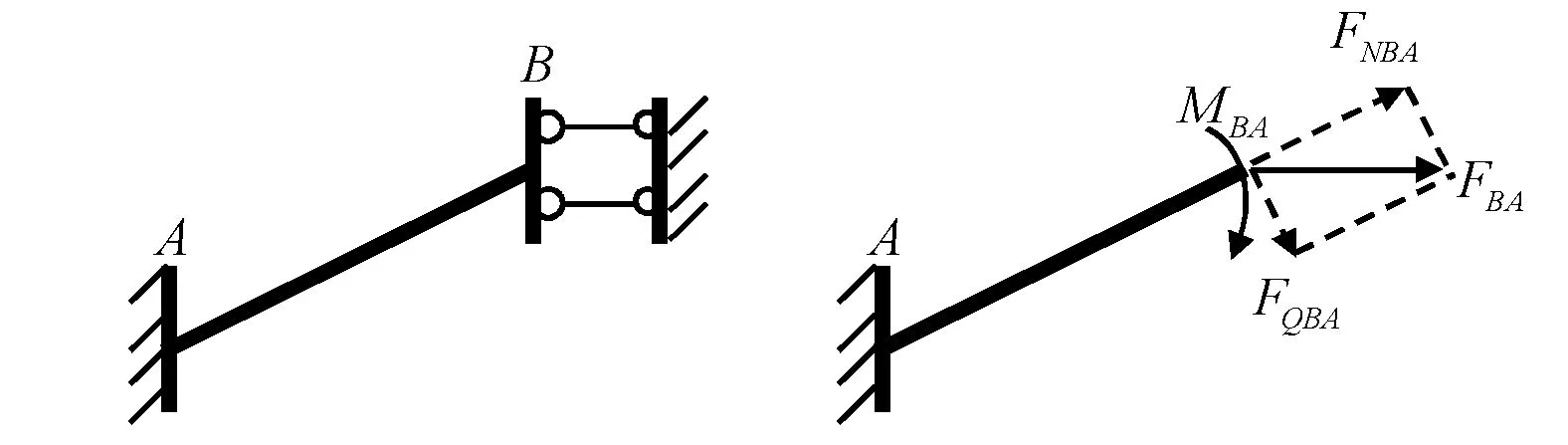
(a) (b)

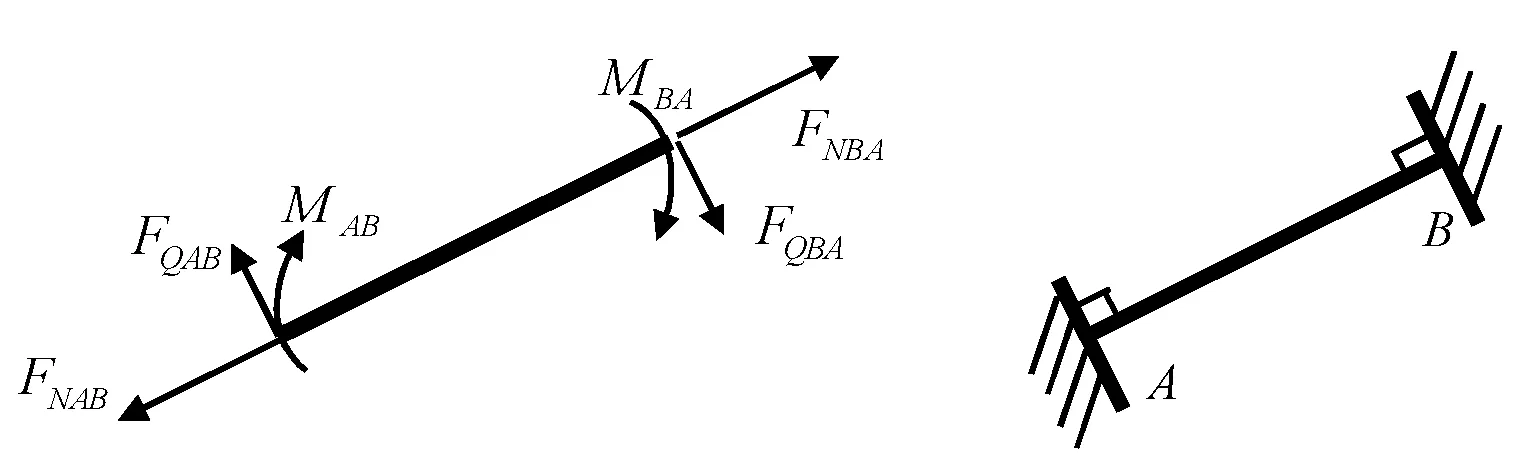
(c) (d) 图19 杆轴线与滑动链杆斜交的单跨

实际上，若从矩阵位移法的视角来看，图1和式(1)～式(4)的分析都属于单元分析，故对于图19(a)所示的单跨结构，可先通过坐标变换，将其转换到局部坐标下，再与图1(a)一样分析。

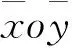
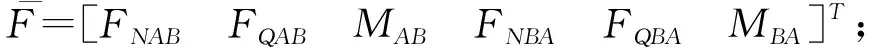
F=[FAxFAyMAFBxFByMB]T；

Δ=[uAxuAyθAuBxuByθB]；

图中所示各量的指向均规定为正向。

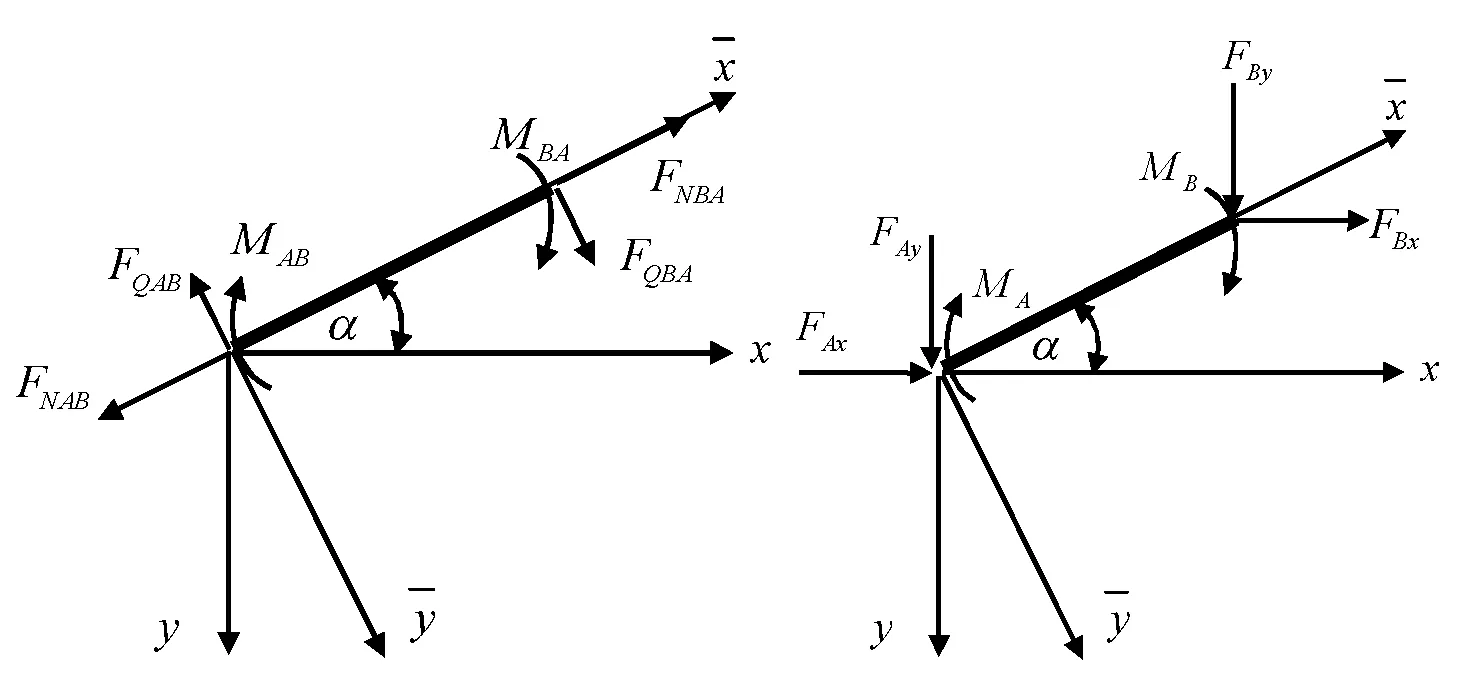
(a) (b)

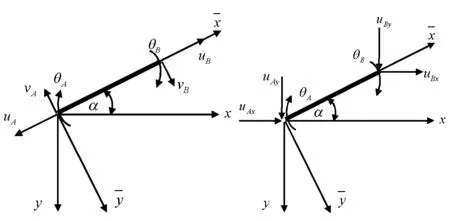
(c) (d) 图20 内力和位移的坐标转换

从图20(c)可见，若忽略轴向变形，则Δl=uB+uA=0，而侧移Δ=vB+vA，由式(8)可得：

-cosα(uAx-uBx)+sinα(uAy-uBy)=0

(9)

Δ=-sinα(uAx-uBx)-cosα(uAy-uBy)

(10)

当滑动向沿y向时，uBx=0，FBy=0，由式(9)可看出，uB=uBy不独立。

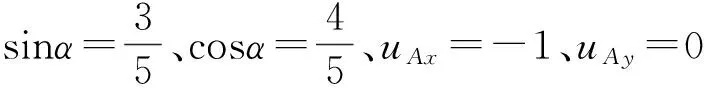
若AB上作用着不垂直于杆轴的荷载，如图21(a)中的Fx、Fy和M，则由坐标转换可得：

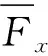
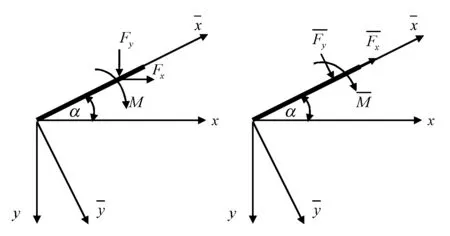
(a) (b)图21 荷载的坐标转换

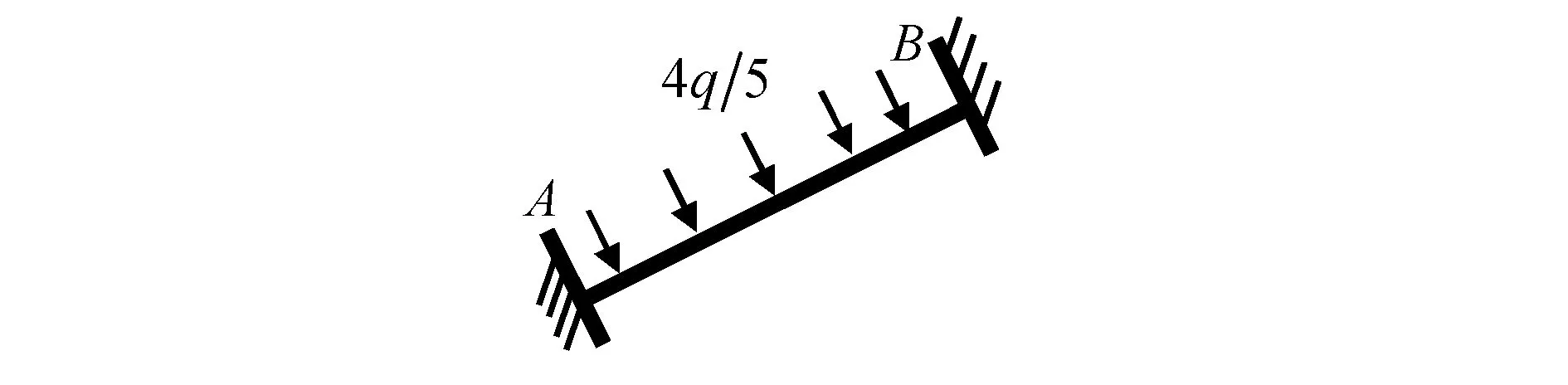
图22 荷载的坐标转换举例

实际上，式(7)～(11)对任意支座形式的斜杆均成立，而不仅限于图19(a)所示的情形。式(9)和(10)可作为求解任意忽略轴向变形的杆件(不仅限于斜杆和滑动支座)两端位移牵连关系的解析式。

综上所述，图19(a)的转角位移方程为：

其中，l′=l/cosα；i′=EI/l′；Δ由式(10)确定，也可按3.3所述的方法确定。

6 对只承受结点集中荷载的无侧移刚架的分析

若忽略轴向变形，对于无侧移(即无结点线位移)的刚架，当只承受结点集中荷载时，弯矩为零[3]，剪力也为零。

利用上述特点，一方面可简化结点荷载作用下自由项的计算，例如图23中，当只考虑结点D处30kN的集中力作用时，各杆均无弯矩和剪力，由D、E处的结点力矩平衡和DEF的水平投影平衡可得：F1P=F2P=0，F3P=-30kN ；另一方面，在作如2.3所述的简化过程中，若静定部分对超静定部分的作用力属于结点集中力，则当无侧移时，不引起弯矩和剪力，可去掉以简化计算，例如图8(d)可简化为图24计算。

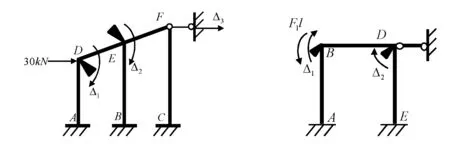
图23 只受结点集中荷载的无侧移刚架图24 图8(d)的简化

7 基本未知量的确定

位移法(手算)和矩阵位移法(电算)不同，后者追求统一性，将所有结点位移加以约束，从而使每一跨都成为两端固定梁，一次性求出所有未知结点位移；而前者则力求计算量少，只通过附加约束，约束住独立的结点位移，将原结构解构为一个个如图1所示的3种基本单跨超静定单元(图19(a)相当于图1(a))和可能存在的静定部分。取独立的结点位移作为自变量，而将其它未知结点位移、杆端弯矩和杆端剪力表示为它们的因变量，如式(1)～式(3)和式(12)所示，故在确定基本未知量时，一定要准确把握“基本”和“未知”两个概念，如图1(c)中，Δ不独立，故非“基本”，θB=0，故非“未知”。

从图1和式(1)中可看出，就某一超静定单跨而言，一个结点位移独立与否，取决于该结点处与之对应方向(轴向、切向和转向)的力(力边界条件)已知与否，若已知，则不独立，否则，独立；结点位移未知与否，取决于与之对应的位移边界条件是否未知。

对图25(a)～(b)所示结构，弯矩和剪力都静定，利用单位荷载法可得：

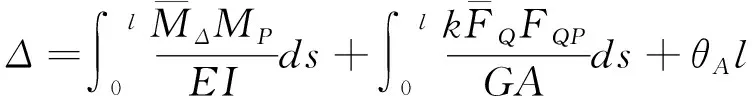
此外，从前述可知，位移牵连(如EA→∞或EI→∞的假设所致)也会减少结点位移的独立性。

(a) (b)图25 弯矩和剪力静定的结构

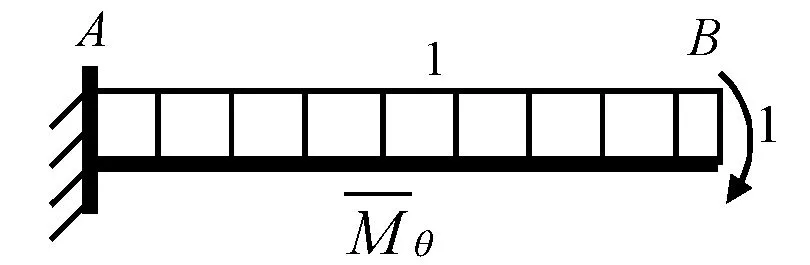
(a)

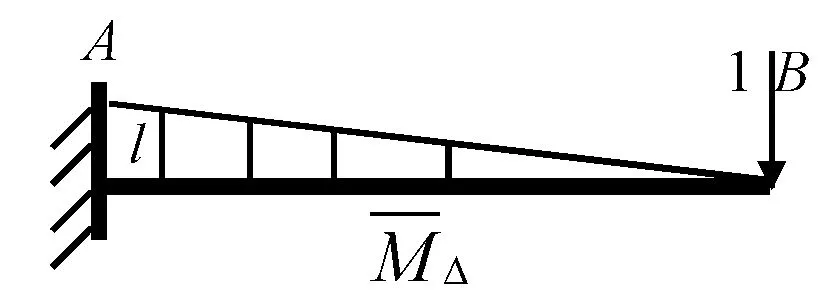
(b)

(c)图26 单位荷载作用下的弯矩图

由图1、图19和图25可见，只有刚结点处的角位移才独立；由图1(c)、图25(a)和图25(b)可见，剪力静定杆的侧移不独立。

外部刚结点(构件与基础或墙体的刚性联结点，即固定支座)处的角位移或为零，或已知，故只有内部刚结点(构件与构件的刚性联结点)处的角位移为独立角位移。此外，还要考虑可能存在的位移牵连对独立角位移的减少。

平面内，一个结点有两个自由度，即两个线位移，在忽略轴向变形的情况下，每根链杆可提供一个沿轴向的约束。故若将所有内部刚结点、外部刚结点、滑动联结和滑动支座处限制转动的约束都去掉，只剩下限制线位移的约束，然后来判断需要添加多少根链杆才能使得剩下的体系几何不变且无多余约束；并减去为限制剪力静定杆如图1(c)、图25(a)和图25(b)所示切向位移而添加的链杆，则沿剩下的链杆向的线位移即独立的结点线位移。利用该法，无需事先将静定部分除去。

为简化分析，可对原结构作一些预处理。因图1(c)的B端解除限制转动的约束后，将如图25(a)所示，又按图7所示的简化模式可知，只受轴力时， 杆连同与之相连的链杆可简化为一根链杆，故对于如图1(c)和图25(a)所示的情况，都可事先简化为如图27所示的情况，而对于如图25(b)所示的全静定部分则可直接去掉。

图27 图1(c)和图25(a)的简化

例如将图28(a)中限制转动的约束(点D、B、C、F处)除去，并添加链杆(点A、B、E处)使之几何不变且无多余约束，但点A、E处附加链杆向的线位移不独立，故只有B点处的线位移为独立结点线位移，此外，也可作如28(c)所示的预处理再分析。同理，图29(b)中点C、D处附加链杆向的线位移不独立，故无独立线位移。由图8的分析可知，F点相当于图25(a)的B端，故图30(b)中点F处附加链杆向的线位移不独立，故只有B点处的线位移为独立结点线位移。

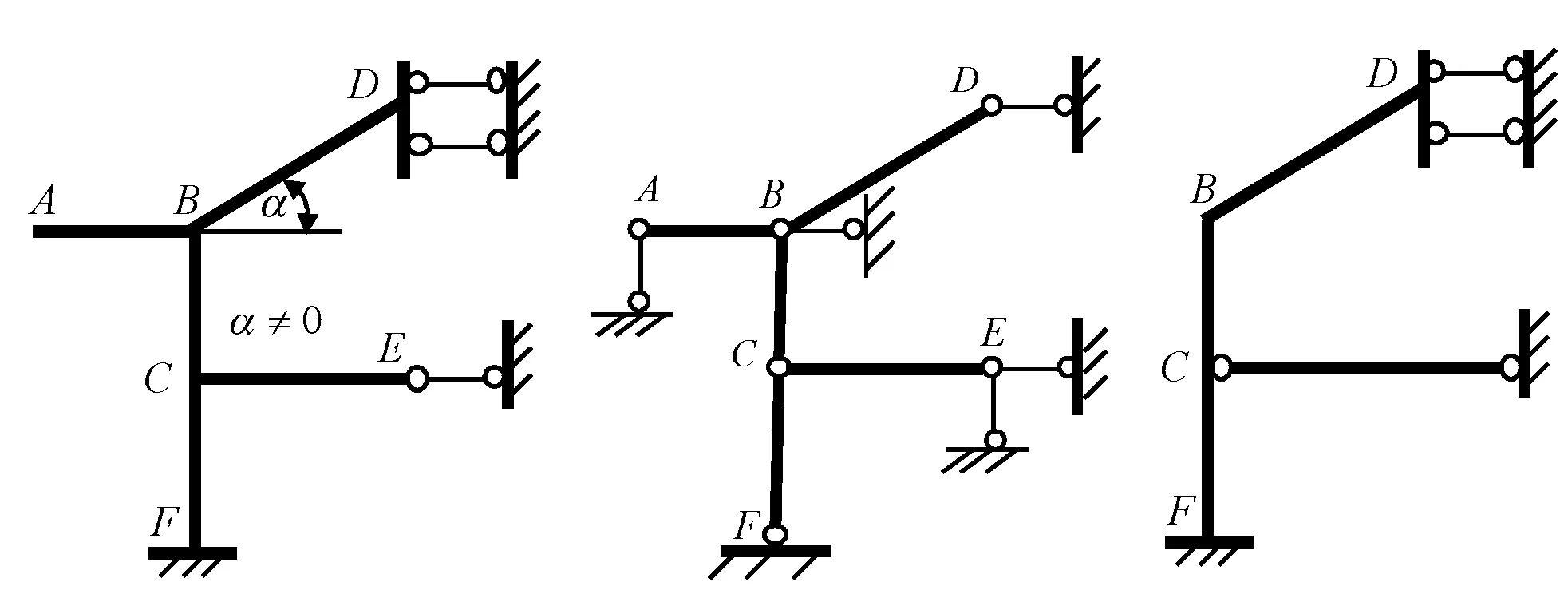
(a) (b) (c) 图28 独立结点线位移的确定举例1

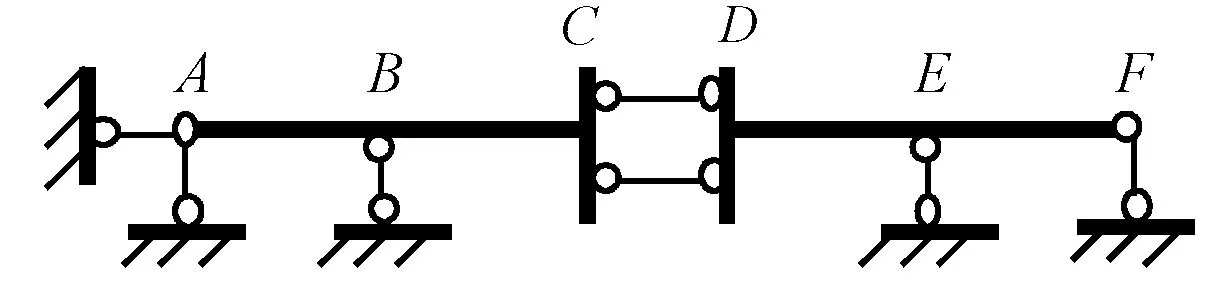
(a)

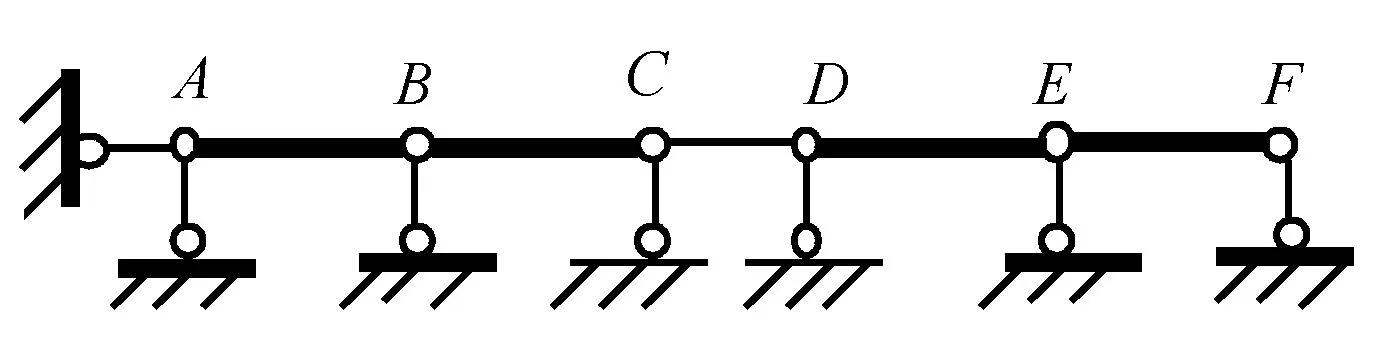
(b)图29 独立结点线位移的确定举例2

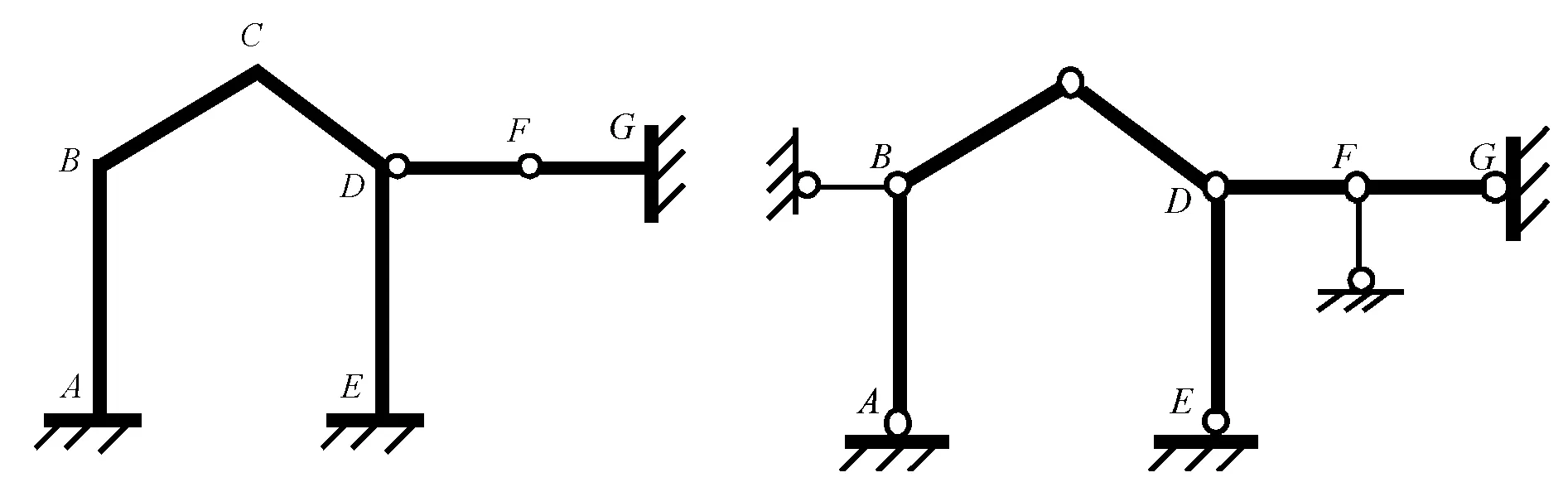
(a) (b)图30 独立结点线位移的确定举例3

8 结论

(1)转角位移方程导出时所基于的前提和假设决定了位移法中基本单元的划分、计算图的简化、基本未知量的选择、位移牵连关系等方面。

(2)位移协调条件和基本未知量的确定等问题，都与同一刚结点处转角相等、EA→∞假设、EI→∞假设等条件相关。

(3)一端固定、一端滑动，且杆件轴线与支承链杆不平行的单跨结构可按两端固定的基本单元处理，但两者之间存在坐标转换关系。

(4)任意忽略轴向变形的杆件两端的位移牵连关系，既可用运动学与几何学的方式求解，也可直接用解析式求解。

(5)将所有内部刚结点、外部刚结点、滑动联结和滑动支座处限制转动的约束都去掉，只剩下限制线位移的约束，然后来判断需要添加多少根链杆才能使得剩下的体系几何不变且无多余约束，并减去为限制剪力静定杆切向位移而添加的链杆，则沿剩下的链杆轴向的线位移即独立的结点线位移。