偶数阶行列积幻阵的构造方法
2018-08-10 07:33:44刘兴祥
重庆理工大学学报(自然科学) 2018年7期
郭 萍,刘兴祥
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
矩阵理论是代数学领域应用十分广泛的研究分支,文献[1-3]是矩阵领域十分重要的研究成果。幻阵具有奇特性质,许多数学家和数学爱好者对其进行了广泛深入的研究。到目前为止,已经发现了幻阵的一些性质和规律[4-8],解决了幻阵的一些问题[9-11],但有关幻阵的未解之谜仍然不少。和幻阵的构造成为矩阵理论领域的研究热点之一,却很少有人研究积幻阵的构造方法。本文通过研究行列和幻阵的构造方法,给出行列积幻阵的构造通法。
1 积幻阵的相关定义


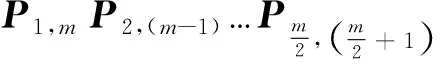
2 行列积幻阵的构造
矩阵C的构造方法如下:

定理1 行列积幻阵Am×n(m=4l,n=4k)的构造方法:
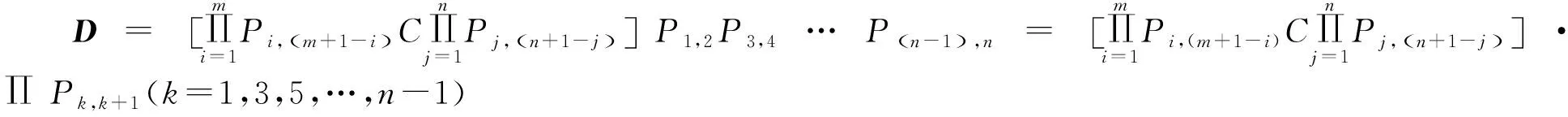
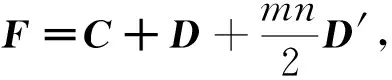
矩阵A= (aij)m×n,其中aij=qfij。

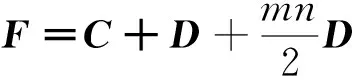

定理2 行列和始元幻阵Am×n(m=4l,n=2k)的构造方法:
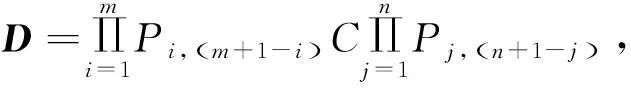


推论1 行列积幻阵Am×n(m=2l,n=4k)的构造方法:将m=4l,n=2k时构造出的行列积幻阵进行转置即可。
证明因为行列积幻阵Am×n的转置是行列积幻阵An×m,所以矩阵An×m仍然是行列积幻阵。
定理3 行列积幻阵Am×n(m=2l,n=2k)的构造方法:

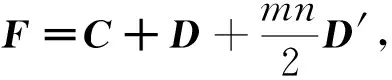

f1,m-1↔f2,m,f2,m-1↔f1,m,fm,n-1↔fm,n
得到矩阵G,,其中G= (gij)m×n。矩阵A= (aij)m×n,其中aij=qgij。

猜你喜欢
电工技术学报(2023年20期)2023-10-31 08:09:26
中等数学(2022年6期)2022-08-29 06:15:08
数学小灵通(1-2年级)(2021年12期)2021-12-30 06:28:00
数学小灵通(1-2年级)(2021年11期)2021-12-02 01:30:04
校园英语·上旬(2019年6期)2019-10-09 04:08:57
测控技术(2018年9期)2018-11-25 07:44:44
中学生数理化·七年级数学人教版(2017年6期)2017-11-09 02:45:57
咸阳师范学院学报(2016年6期)2017-01-15 14:18:38
厦门理工学院学报(2016年1期)2016-12-01 04:50:52
新疆大学学报(自然科学版)(中英文)(2014年3期)2014-11-02 07:52:38

