基于包容性检验的新疆兵团农机总动力组合预测

王丽伟，赵永满，杨续昌，付 威，曹卫彬，周 雪

(石河子大学 机械电气工程学院，新疆 石河子 832000)

0 引言

新疆生产建设兵团(以下简称“兵团”)农机总动力数值是衡量兵团农业机械化发展水平高低的重要指标之一，较高精度的预测值可为兵团相关部门制定农业机械化发展政策提供重要的参考依据[1]。自2005年以来，兵团在中央政策和资金扶持下[2]，大力推动实施农机购置补贴政策，在很大程度上调动了农民购买农业机械的积极性，使得农机总动力快速的增长。在2000-2012年的13年中，兵团农机总动力保持平稳较快的增长趋势，年平均增长率为4.43%，总动力数值增长了2.54倍；截止到2014年末，兵团农机总动力已达487.55万kW(资料来源：兵团统计年鉴2000-2014年)。兵团农机总动力的增长对加速发展兵团农业机械化，实现兵团农业现代化等有很大的指导作用。因此，对兵团农机总动力进行预测不仅可以为兵团农业机械生产部门提高科学准确的生产依据，而且能够为兵团经济决策提供参考依据，具有重要的现实意义。

在日常的生产和生活中，决策者通常使用不同的预测模型对同一事物进行预测，不同的预测模型因基于不同的信息集而会得到不同的预测结果，其预测精度也会不同[3-4]。由于农机总动力的增长受多种因素的影响，使得对其进行精确的预测具有很大的难度。尽管已有不少学者从不同的角度采用不同的方法对兵团农机总动力预测问题进行了一些研究[5-7]，但这些方法对数据样本预测的误差较大，不能取得令人满意的效果。吐尔逊·买买提[8]等人在充分挖掘原始数据信息的基础上，通过构建组合预测模型使预测精度得到了一定的提高。针对回归模型的多重共线性及灰色模型仅含有指数增长趋势的问题，刘银萍[9]等人建立了主成分回归和灰色回归两种预测模型，对预测结果进行对比表明：灰色回归模型的预测精度较高，能较准确地刻画兵团农机总动力的总体变化趋势。

在应用组合预测方法时，决策者通常是仅凭借经验或者数据特征列出可能合适的模型，并通过这些模型寻找一种最优的组合形式来进行预测。正是在这样的主观判断下，组合预测仍然存在一些需要解决的问题。文献[10]表明并不是所有的组合模型预测精度总是高于单项预测模型的精度，在实际的预测中只能表明：采用组合预测模型进行预测所带来的风险小于采用单项预测模型带来的风险。文献[11]表明：随着组合预测模型中单项预测模型数目的增多，预测精度反而在减小。这就说明，在构建组合预测模型前，有必要挑选出对提高组合预测模型精度有帮助的单项预测模型。文献[4]指出，最终构建的组合模型中的各单项模型之间存在的相关性会降低组合预测模型的精度。为解决此问题，文献[12]利用两两组合预测模型相互包容检验的方法，并将该方法应用到单项模型的选择中。但这种方法没有解决组合后模型中的各单项模型可能包含组合前不包含的单项模型的问题，使得组合后的模型仍然包含冗余信息[13]。文献[14]以预测性能相对较好的单项模型为基础模型，通过依次往模型中增加单项模型进行组合，并利用包容性检验对组合前后的模型进行评价，得到最优的组合模型。但在权重值的分配上，文献[14]采用的是等权重分配方法，此方法虽简单，但对于长期预测来说，不变权重组合预测在预测效果上难以达到令人满意的结果。针对文献[14]中采用不变权重法分配权重值的问题，文献[13]通过最优加权法根据预测模型精度的不同，分配不同的权重，提高了预测的精度。本文在文献[13-14]的研究基础之上，通过使用包容性检测原理来选择合适的单项预测模型，并利用基于误差均方根倒数法求解组合预测模型的权重值，构建组合预测模型，并使用构建的组合预测模型来预测兵团农机总动力，达到提高预测精度的目的。

1 组合预测理论

自JM Bates和CWJ Granger提出“组合预测”思想以来[15]，现已发展成为现代预测科学理论的重要组成部分。组合预测模型能充分利用多个单项预测模型所包含的信息，对多种预测效果进行总体性评价，预测效果比单项预测模型更精确。

设ft为农机总动力组合预测模型t年的预测值，yt为t年的真实值，fti为第i种单项预测模型t年的预测值，ki为第i种单项模型的权重值，i和t取值均为1至n，则组合预测模型具有如下结构

(1)

∑ki=1

确定组合模型中权系数的方法有很多，可以基于误差均方根、平均绝对百分误差等相关性指标。求解式(1)的关键是确定各单项预测模型的权重。为确定各权重，可以以误差平方和最小为目标构建以下模型，即

(2)

且满足下列条件

(3)

其中，Q表示误差平方和;et表示t时刻组合预测模型的误差。由式(3)可得

km=1-(k1+k2+…+km-1)≥0

(4)

2 包容性检验原理及流程

2.1 包容性检验原理

包容性检验用于检验并判断某种预测模型是否包含其他的预测模型[13]。通过对相关文献的学习，本文将采用依次向组合模型中增加单项模型的方法来进行包容性检验。如有m种单项预测模型，采用此方法可使得检验次数由传统的2m-m-1减少到m-1次，大大提高了检验效率。

设Q1、Q2为两种单项模型，它们对兵团农机总动力第t年的预测值分别为f1,t和f2,t，则有

yt=β1f1,t+β2f2,t+σt

(5)

其中，β1和β2为回归系数；σt为随机扰动。

在式(5)中两边同时减去f1,t，则有

yt-f1,t=β1f1,t+β2f2,t+σt-f1,t=
β2[(yt-f1,t)-(yt-f2,t)]+σt

(6)

令ei,t=yt-fi,t(i=1,2)，则式(6)就可以转化为

e1,t=β2(e1,t-e1,t)+σt

(7)

同理，通过在式(5)两边同时减去f2,t，化简可得

e2,t=β1(e2,t-e1,t)+σt

(8)

通过构建式(7)和式(8)就能分别检验β2或β1是否为零，利用检验结果来判断模型的包容性。文献[16]已经证明可通过使用t统计量来判断β1或β2是否为零，并给出了相应的计算过程。本文将通过利用t统计量来检验式(7)中β2=0的显著性。检验步骤如下：

1)提出假设。H0∶β2=0，H1∶β2≠0。

3)确定显著性水平α。查t分布表确定其临界值。

4)检验结果的判定。如果计算的t统计量的绝对值大于临界值，即|t|>tα/2(n-2)，则拒绝原假设，认为两单项模型不相互包容，可以进行组合将两模型组合并标记成新的基础模型；反之，若计算的t统计量的绝对值小于临界值，则接受原假设，认为两单项模型相互包容，则剔除加入包容检验的单项模型。

5)若所剩待检验单项模型的数量不为零，则重复步骤1)～4)，提出新的假设量并计算其统计量t值。若所剩待检验单项模型的数量为零，结束包容性检验，进行基于误差均方根倒数法的模型组合，计算兵团农机总动力的预测值。

2.2 包容性检验选择基本预测模型的流程

将包容性检验原理应用到选择单项模型的思想，最早可以追溯到文献[17]中。目前，对包容性检验的研究大都局限于两种单项预测模型组合时的情况，但在对多个模型进行包容性检验的过程中，未能考虑多个模型组合后可能包含组合前不包容的单个模型的情况。针对以上研究中存在的不足，本文将采用依次向基本模型中增加单项模型并构建组合模型，并利用包容性检验对组合前后的模型进行对比分析的方法，来选取组合模型中各单项预测模型。利用包容性检验原理选择单项预测模型的流程如图1所示。

图1 包容性检验选择单项预测模型的流程图

3 新疆兵团农机总动力的组合预测

农业机械化是兵团农业发展的基础，也是兵团农业经济发展的支撑。段亚莉[18]等人通过构建农业机械化发展水平评价指标体系，对全国农业机械化的发展状况进行评价，表明新疆兵团农机化发展水平综合排序仅次于黑龙江，位居全国第二。而农机总动力拥有量是衡量兵团农机化发展水平的重要指标之一，对其进行较高精度的预测具有重要的意义。本文将选取兵团1989-2014年农机总动力为数据源，分别建立指数平滑法f1、灰色预测模型f2、参数法预测模型f3、指数法预测模型f4等二次多项式法f5，三次多项式法f6，6种单项预测模型，原始数据及预测值如表1所示。

为了客观地评价各个单项预测模型的预测精度，本文将采用均方根误差(Root Mean Squared Error，RMSE)作为预测性能的评价指标，即

(9)

其中，i=1,2,3,…,6。在进行组合包容性检验时，组合预测模型的组合权系数都按照预测误差均方根倒数法确定，从所有单项预测方法中选出若干最优模型，并建立组合预测模型。表2给出了两两组合预测模型误差。

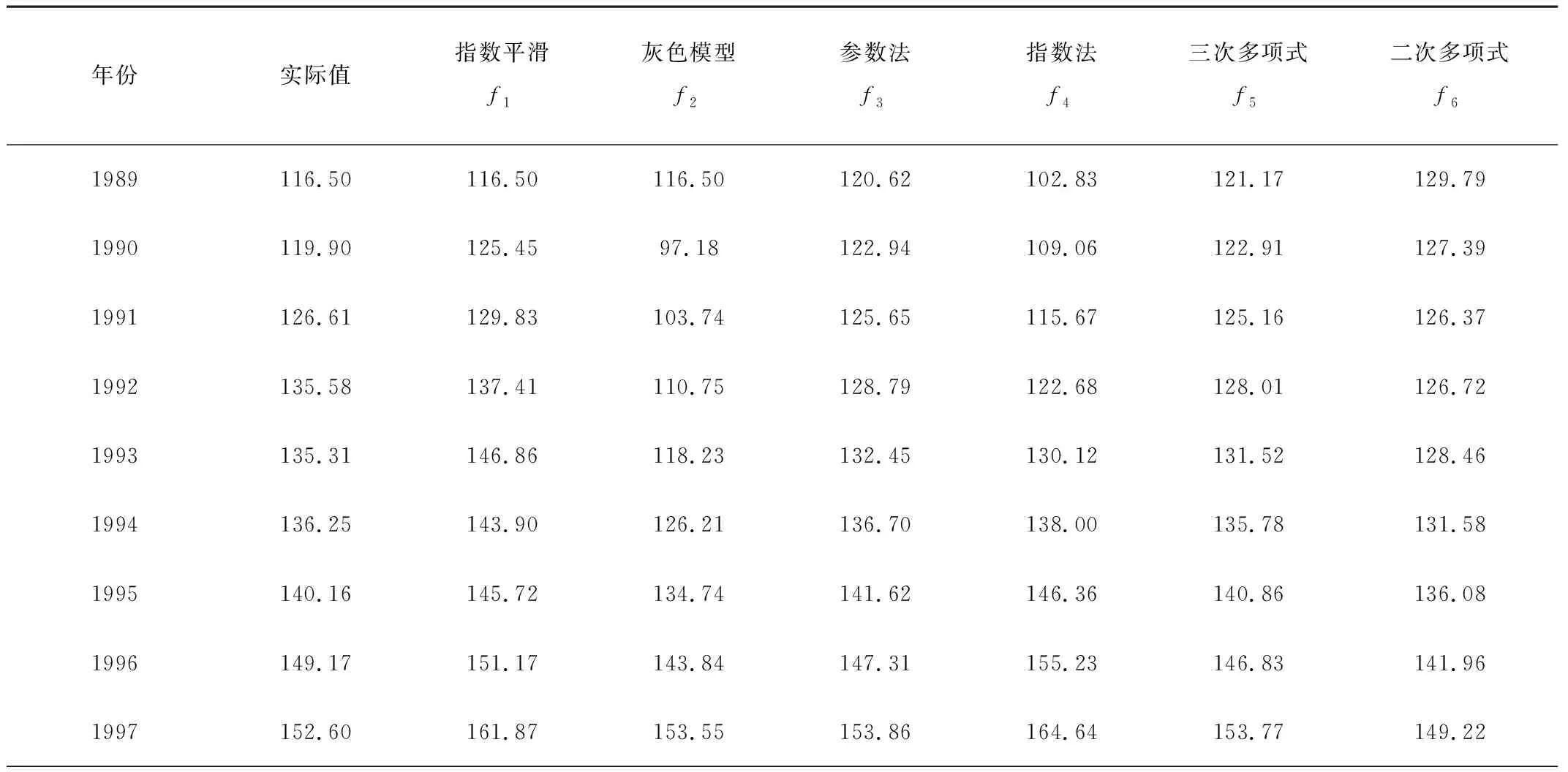
表1 新疆兵团农机总动力实际值及预测值

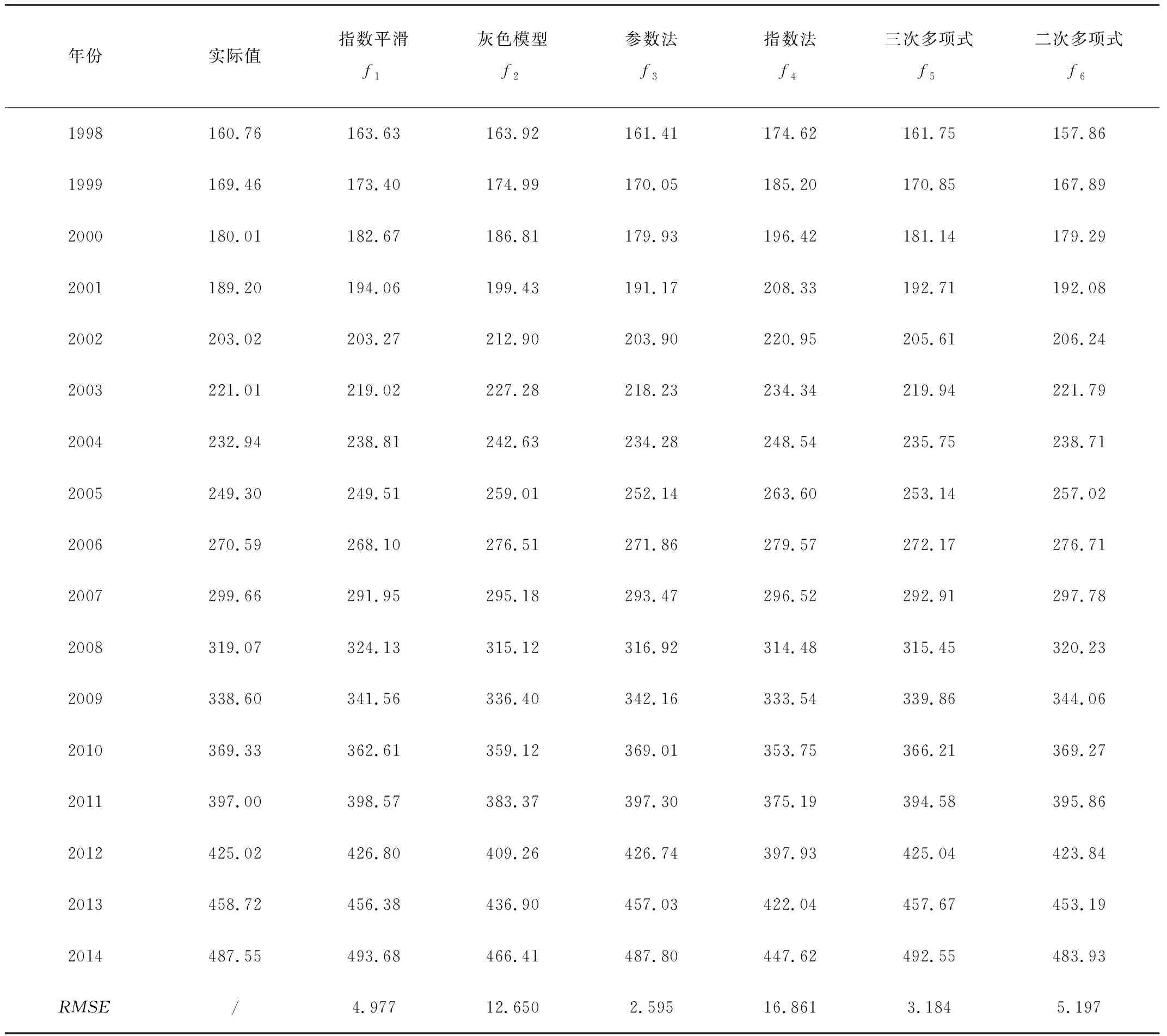
续表1 104kW

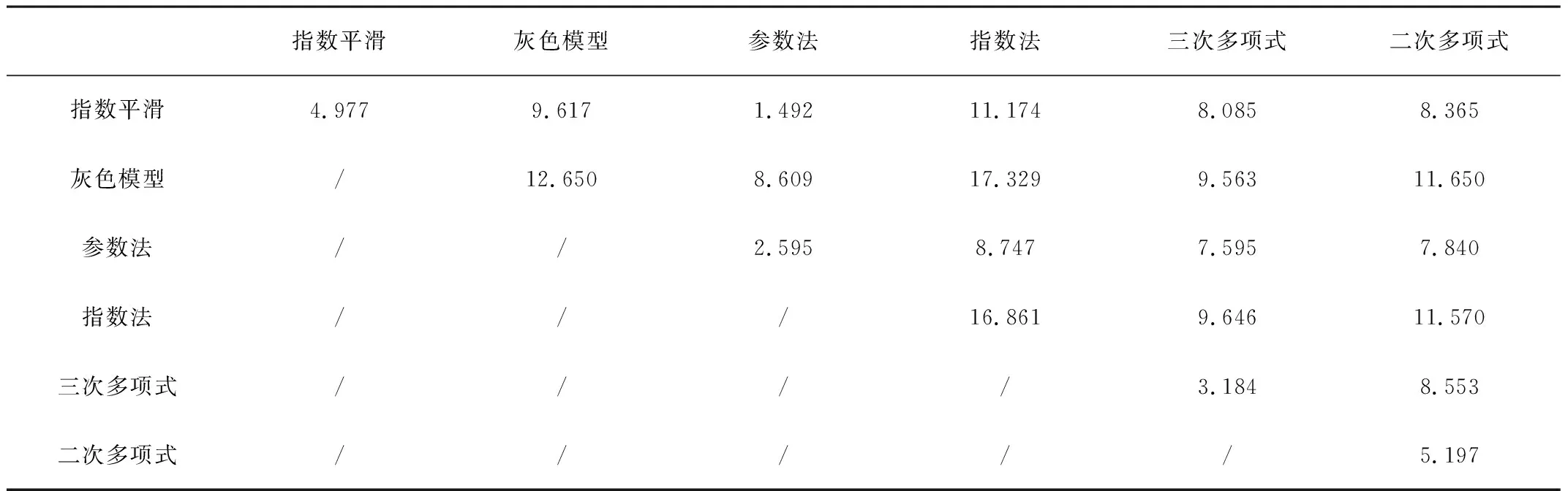
表2 各单项模型及两两组合预测模型均方根误差表

表2中对角线位置的数据表示采用单一预测模型时模型预测精度的RMSE，表格内其余的数据表示两两不同预测模型采用误差均方根倒数法组合后的组合模型的RMSE。从表2中可以看出：组合模型预测的精度至少高于组合模型中精度最差的单项模型预测的精度，但不少组合后的模型预测精度要比组合前单项模型预测中最好的精度要差。以上分析说明：有必要通过包容性检验来选择合适的单项模型，用以提高组合预测精度。根据图1提出的包容性检验选择单项预测模型的流程图对上例进行分析，步骤如下：

1)根据表1和表2对各单项模型预测精度进行由高到低的排序为：f3参数法 >f5三次多项式 >f1指数平滑 >f6二次多项式 >f2灰色模型 >f4指数法。首先选取预测模型精度最好的f3参数法为基本预测模型。

2)在显著性水平α=0.05的情况下，对f3模型和f5模型进行包容性检验。通过计算得t统计量为-0.507，查表得t0.025(24)=2.064，由于|t|=|-0.507|<2.064。接受原假设，认为模型f3包容模型f5，将模型f5剔除不再考虑组合；然后，将模型f3和模型f1进行包容性检验，得t统计量为2.879，由于|t|=|2.879|>2.064，则拒绝原假设，认为模型f3不能包容模型f1，将模型f3与f1进行基于误差均方根倒数法的组合预测，并将组合模型f31标记为新的基本预测模型。

3)在显著性水平α=0.05下，将组合模型f31与模型f6进行包容性检验，得t统计量为0.750。由于|t|=|0.750|<2.064，则接受原假设，认为模型f31包容模型f6，将模型f6剔除不再考虑组合；然后，将组合模型f31与模型f2进行包容性检验，得t统计量为0.278。由于|t|=|0.278|<2.064，则接受原假设，认为模型f31包容模型f2，将模型f2剔除不再考虑组合。最后，将组合模型f31与模型f4进行包容性检验，得t统计量为-0.098 4。由于|t|=|-0.098 4|<2.064，则接受原假设，将模型f4剔除不再考虑组合。此时，待检验包容的单项模型数量已经为空，结束包容性检验。

4)将组合模型f31作为最终预测模型，对2010-2014年兵团农机总动力数据进行预测和精度评价。同时，采用未经包容性检验直接将所有各单项模型进行等权重组合对兵团农机总动力进行预测及精度评价，预测及评价结果如表3所示。

表3 包容性检验的组合模型精度对比

由表3中可以看出：①通过包容性检验的组合模型预测精度为4.32，相比未通过包容性检验的组合模型的精度18.72，预测精度上提高了14.4，因此可以证实在构建组合预测模型时很有必要进行包容性检验，用以选择合适的单项预测模型。②本文选用的基于误差均方根倒数法的组合预测模型相比传统的基于等权重构建的组合预测模型，预测精度和预测效率上都有一定程度的提高。

4 结论

本文在组合预测研究的基础上，应用包容性检验原理对单项预测模型进行检验，通过检验结果选择合适的单项预测模型，并应用基于误差均方根倒数法分配权重，用以构建组合预测模型，与传统的组合预测方法相比预测精度有了很大的提高。运用本文构建的组合模型对兵团2015-2016年农机总动力进行预测，预测结果分别为520.17、546.09万kW，预测结果在一定程度上会为兵团经济决策提供参考依据。