地表均布超载作用下软土地区既有盾构隧道对地层相对挤压量的计算方法

黄大维，周顺华，冯青松，刘林芽，徐金辉，涂文博

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；2.同济大学 道路与交通工程教育部重点实验室，上海 201804)

对于软土地区的地铁盾构隧道，从所掌握的现场调研资料分析来看，在施工完成后，虽然可以满足相关规范的要求，但在现有分析计算理论所允许的地表超载(盾构隧道施工完成后进行地面堆土、堆放材料设备、或其他工程活动导致荷载均称之为地表超载)作用下，极易发生横向变形过大，导致管片接头的张开量明显超限，并由此引发隧道结构不同程度的破损与渗漏水，可见地表超载是盾构隧道设计过程中必须考虑的一项重要荷载。同时，在运营期，若受到频繁的工程影响，则不可避免地会出现地表超载，因此，地表超载对既有盾构隧道的影响不可忽视。

对于盾构隧道施工完成后的地表超载，《地铁设计规范》[1]建议换算为隧道施工前对应上覆土层的厚度或地表均布荷载予以考虑。文献[2]针对地面堆载导致上海饱和软土地层既有盾构隧道变形过大的问题，采用室内模拟试验和数值仿真的方法，分析了既有隧道埋深、地表超载量、超载位置等参数对盾构隧道变形的影响。文献[3]采用数值模拟方法研究了地表超载、侧土压力系数和土体抗力系数对隧道横向变形发展的影响，分析了隧道横向变形随地表超载的变化发展规律。但现有研究一般只定性地分析地表超载对既有盾构隧道变形的影响[4-6]，难以从机理上解释地表超载导致既有盾构隧道变形超限的机制。

本文根据1∶10室内模型试验测得的土层沉降及隧道变形，分析地表超载作用下既有盾构隧道与地层的相互作用，推导地表超载作用下既有盾构隧道与地层相对挤压量的计算公式，为下一步分析地表超载导致既有盾构隧道周围附加土压力的解析计算方法奠定基础。

1 现有理论存在的问题

在分析地表超载导致既有盾构隧道的附加土压力时，将地表均布超载换算为相应的上覆土层厚度[7-8]，或将地表局部超载按弹性理论计算出地表超载传递到隧道顶部的荷载[9-10]，如布辛尼斯克(Boussinesq)与威斯特卡德(Westerguard)等理论方法，均人为地将地表荷载视为作用于完全土质的地层。所谓完全土质的地层，是相对于存在盾构隧道的地层(如图1(a))而言的，即在对应的位置不存在盾构隧道的地层(如图1(b)所示)。为了便于叙述，将对应的位置命名为“虚拟隧道”，虚拟隧道与盾构隧道的外边界完全相同。图1中：D为盾构隧道的外直径；S1为盾构隧道上覆土层的厚度；S2为盾构隧道穿越土层的厚度，则S2=D；S3为盾构隧道下卧土层的厚度，其深度取到土压力基本不受盾构隧道影响的位置。

图1 两种不同的地层

在地表超载过程中，按照现有土柱理论的土压力计算方法，在均布地表超载q作用下，盾构隧道和虚拟隧道附加的竖向土压力均为q，水平土压力均为λq(其中λ为侧土压力系数)。然而，从平面应变角度来看，盾构隧道属于以弯曲变形为主的曲梁结构，在地表超载作用下盾构隧道结构变形与土层中土体变形特性不同，因此图1(a)中盾构隧道的位移与图1(b)中虚拟隧道的位移并不相同，两者位移的不同说明盾构隧道对周围土体形成了相对挤压。由此可见，现有土柱理论忽略了该相对挤压对盾构隧道周围土压力的影响，因而所得到的土压力与实际不符。

2 地表均布超载作用下盾构隧道与地层的相互作用分析

考虑到模型试验是为了探索地表超载作用下盾构隧道与周围土体的相互作用机理，在上部逐步填土过程中，将某一个土层厚度作为既有填土，再增加的填土层则可作为地表超载，其隧道变形及隧道顶部与底部位置的土体竖向沉降总体趋势都是相同的。该室内模型试验未采用盾构施工的方法将盾构隧道埋入地层中，而是采用上部土体一层一层地填筑。

2.1 试验模型及结果分析

地表超载室内模型试验是以上海通缝拼装的地铁盾构隧道为原型隧道，采用的几何相似比为1∶10，容重相似比为1∶1，其余各物理量的相似常数见文献[11]。模型试验分为1号和2号2个模型，关于模型盾构隧道、模型槽、模型土、试验方法以及相关误差等均见文献[11]和文献[12]。试验时，逐层增加上覆土厚度，分别对土体沉降和隧道变形进行测试，其中土体沉降通过土体中的沉降刻度板及模型槽壁上的钢尺之间的关系读出，其布设的位置如图2所示，隧道变形采用布设在中间管片环内的位移传感器量测，位移传感器每隔45°布设1个。

图2 土体沉降测点布置位置示意图(单位：cm)

图3与图4分别为图2所示的隧道顶部位置与隧道底部位置的土体沉降(沉降取负值；水平距离位于隧道中线的左侧取负值，位于右侧取正值)，其中D=0.62 m。从图3可以看出：1号和2号模型隧道顶部土体的沉降总体趋势接近，均为隧道正上方位置土体的沉降量较小，两侧的沉降量较大，且随着上部堆载的逐渐增加，隧道正上方土体与其两侧土体的沉降差也在逐渐增加；1号模型隧道上覆土体间的沉降差大于2号模型，这是因为隧道穿越土层的压缩模量较小。图4中1号和2号模型隧道底部土体的沉降总体趋势也接近，均为隧道正下方位置土体的沉降量大，而其两侧土体的沉降量小。

图3 不同上覆土层厚度时隧道顶部位置的土体沉降

图4 不同上覆土层厚度时隧道底部位置的土体沉降

隧道顶部位置与底部位置土体的沉降之差就是隧道穿越土层的竖向压缩量，计算当隧道顶部上覆土层厚度为2.75D时隧道穿越土层的竖向压缩量，结果如图5所示，其中与隧道中心间水平距离为0处的隧道穿越土层的竖向压缩量刚好等于隧道竖向收敛变形，如图6所示。由图5与图6可知：在隧道上覆土层厚度逐渐增加的过程中，隧道竖向变形要小于隧道两侧土层的竖向压缩量；隧道穿越土层的压缩模量较小，隧道竖向变形与隧道两侧土层的竖向压缩量之间相差越大，在相同的上部填土荷载作用下，隧道的水平变形和竖向变形也越大。

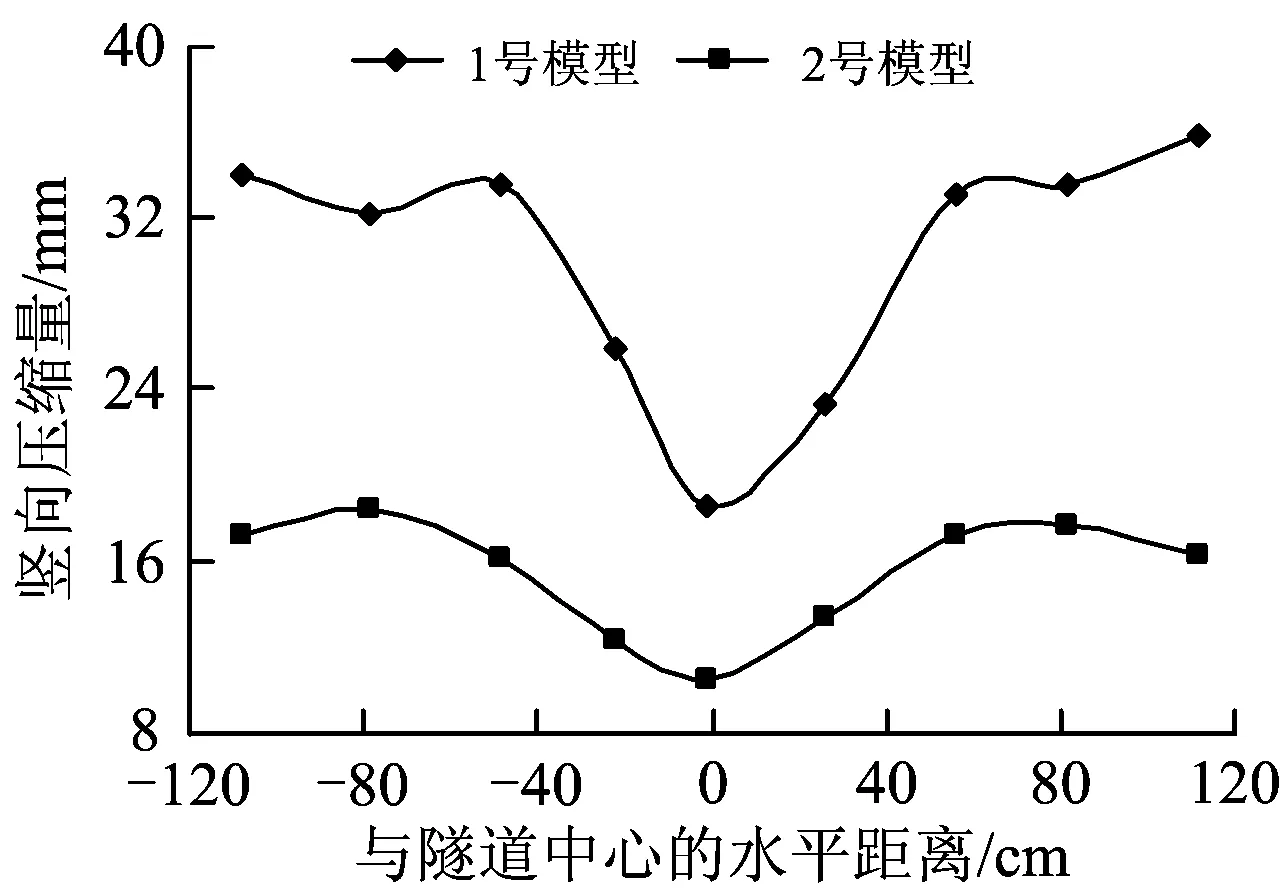
图5 隧道上覆土层厚度为2.75D时隧道穿越土层的竖向压缩量

图6 隧道收敛变形

2.2 盾构隧道与地层的相互作用分析

为了在分析地表均布超载作用导致盾构隧道周围的附加土压力时考虑盾构隧道对周围土体形成的相对挤压，根据模型试验得到的土体沉降和隧道变形规律，在此提出“两状态对比分析法”，其中两种状态的定义如下。

状态2：对完全土质的地层(图1(b))在地表施加均布超载q，如图7(b)所示。

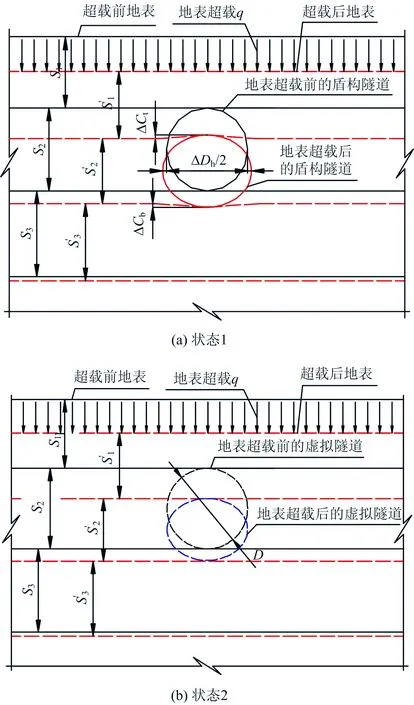
图7 两状态对比分析示意图

采用“两状态对比分析法”可以进行位移对比和土压力对比两方面的研究，但本文仅对“位移对比”进行研究。

位移对比：计算状态1中隧道的位移与状态2中虚拟隧道位移的差值，该位移差则可认为是盾构隧道对周围土体的相对挤压量。

土压力对比：计算状态1中隧道的附加土压力与状态2中虚拟隧道附加土压力的差值，该土压力差则可认为是盾构隧道对周围土体相对挤压导致的土压力。

3 地表均布超载作用下地层与既有盾构隧道的变形分析

以地表超载前隧道横断面的中心作为局部坐标原点建立平面坐标系，基于盾构隧道的变形特性，将图7中地表超载前后的盾构隧道和虚拟隧道均放在该平面坐标系中，如图8所示。由图8可知，地表超载过程中，盾构隧道不仅对侧部一定范围内的土体形成水平向相对挤压，同时对隧道上部与下部一定范围内的土体形成竖向相对挤压。

3.1 完全土质地层的土体压缩变形

图8 盾构隧道对周围土体的相对挤压分析示意图

设完全土质地层中虚拟隧道穿越土层土体的压缩模量为Es2，则在地表均布超载作用下，完全土质地层发生一维压缩变形，其压缩应变ε2及虚拟隧道穿越土层的压缩量ΔS2的计算公式分别为

(1)

(2)

虚拟隧道的变形与其周围地层保持“绝对变形协调”，即对周围土体不存在相对挤压。以虚拟隧道中心作为局部坐标的原点，在地表超载过程中，虚拟隧道整体向下发生移动，如图7(b)所示，但局部坐标原点也相应地向下发生移动。当将虚拟隧道用局部坐标表示时，则地表超载前后虚拟隧道的相对位置关系如图9所示。图中：R为隧道结构的外半径，R=D/2；α为虚拟隧道上任意点到圆中心的连线与Y的正半轴所成的角度，以顺时针方向为增加方向。

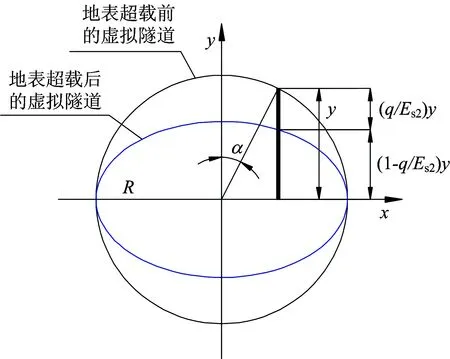
图9 地表超载前后的虚拟隧道

尽管地表超载前的盾构隧道存在一定的横椭圆变形，但相对隧道尺寸而言，该变形很小。为此，假设地表超载前盾构隧道为标准的圆形结构，也即地表超载前的虚拟隧道为标准的圆形结构，其y坐标的计算式为

(3)

隧道穿越土层因地表超载发生竖向压缩，虚拟隧道上半圆对应高度为y的土柱，其竖向压缩量Δy为

Δy=ε2y前

(4)

则地表超载后虚拟隧道y坐标的计算式为

y虚=y前-Δy

(5)

3.2 盾构隧道的变形

在地表超载作用下，盾构隧道表现为横椭圆变形。当从平面应变角度考虑时，盾构隧道可视为曲梁结构，由此对隧道侧部土体形成水平挤压而产生水平地层抗力。

为了更直观地看出地表超载作用下盾构隧道的变形，将模型试验中的盾构隧道的尺寸减小10倍，即外径为62 mm，再将隧道结构的变形按实测结果绘制到图中，此时隧道结构的变形将被相对地放大了10倍。图10为1号模型试验在竖向收敛变形ΔDv分别为5.7与13.1 mm、水平收敛变形ΔDh分别为5.0与11.5 mm时测得隧道结构变形。在图中以“a=R+ΔDh/2”作为椭圆的长半轴、以“b=R-ΔDv/2”作为椭圆的短半轴绘制出相应的标准椭圆。

从图10可以看出，模型试验过程，隧道变形实测结果与标准椭圆非常接近。为了方便对隧道变形过程进行表述，在此假设盾构隧道变形后为标准椭圆形状，即可用标准椭圆的方程表达变形后的盾构隧道。此外，由结构力学理论可知，结构因轴力及剪力导致的变形要远小于因弯矩导致的变形，因此，盾构隧道在变形过程中，任意椭圆状态下的周长与变形前盾构隧道的周长保持相等。

变形后盾构隧道y坐标及其周长L的计算式分别为

(6)

L=2πR=2πb+4(a-b)

(7)

根据a=R+ΔDh/2与b=R-ΔDv/2，并结合式(7)，可以得到ΔDh与ΔDv的关系式为

(8)

图10 隧道变形与标准椭圆的比较

4 既有盾构隧道对地层相对挤压量的计算

首先假设存在如下过程(实际中并不存在以下过程)：在地表超载作用下，盾构隧道先变为变形后的虚拟隧道(此时均布地表超载q导致的隧道附加竖向土压力为q，附加土压力增量为λq)；然后再将变形后的虚拟隧道变为变形后的盾构隧道。

4.1 水平相对挤压量的计算

盾构隧道被压扁的过程中，因水平直径增大，隧道对其侧部土体产生了明显的水平相对挤压，由此将导致水平地层抗力，如图11所示。为了下一步定量地计算地表超载作用下的水平地层抗力，在此根据变形前的盾构隧道与变形后的盾构隧道之间的几何关系(如图11所示)，计算出隧道发生横椭圆变形过程中对侧部土体的水平相对挤压量Δh。

基于隧道结构及其变形的对称性，在此只分析图11中正半轴部分的水平相对挤压，根据式(3)和式(6)可得到盾构隧道变形前与变形后在x正半轴上的水平坐标计算式分别为

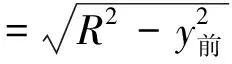
(9)

(10)

隧道对其侧部土体的水平相对挤压量Δh为

Δh=x后-x前

y前∈[-n,n]；y后∈[-n,n]

(11)

图11 水平相对挤压示意图

图11中交点A与坐标原点o的连线与y轴正方向所成角度β的计算式为

(12)

则图11中水平地层抗力范围θ的计算式为

θ=π-2β

(13)

根据式(8)及式(11)得到外径为D=6.2 m的盾构隧道在竖向收敛变形分别为ΔDv=20，100，200和300 mm状态下其水平相对挤压量如图12所示。

图12 隧道对侧部土体的水平相对挤压量

从图12可以看出：水平相对挤压量可近似为三角形，因此，以往水平抗力近似地取为三角形是可行的；此时水平地层抗力范围θ约与72°，而传统的水平地层抗力范围θ均人为地取为90°是缺乏相关理论依据的。

4.2 竖向相对挤压量的计算

在图8中，变形后的虚拟隧道变为变形后的盾构隧道过程中，不仅对隧道侧部土体产生了水平相对挤压，同时对隧道周围土体还产生了竖向相对挤压。除了图11所示的水平相对挤压，其他挤压则认为是竖向相对挤压，如图13所示，因隧道对周围土体的竖向相对挤压量完全对称，在此只分析图13中y轴正半轴部分的竖向相对挤压。根据变形前的盾构隧道、变形后的虚拟隧道及变形后的盾构隧道之间的几何关系，如图13所示，可以得到地表超载后隧道对周围土体的竖向相对挤压量表达式如下。

图13 竖向相对挤压示意图

(1)当x∈[-m,m]时，根据式(5)和式(6)得到竖向相对挤压量的计算式为

(14)

(2)当x∈[-R,-m]及x∈[m,R]时，根据式(3)和式(5)得到竖向相对挤压量的计算式为

(15)

图14 隧道对周围土体的竖向相对挤压量

由以上分析可知，相对挤压量与隧道结构变形有关，也即与隧道结构刚度有关；此外，相对挤压量还与隧道穿越土层的压缩量有关，也即与隧道穿越土层的压缩模量有关。

5 结 论

(1)传统方法计算地表均布超载导致既有盾构隧道的附加竖向土压力等于地表均布超载，忽略了地表超载过程中盾构隧道对地层的相对挤压作用，因而所得到的盾构隧道周围的附加土压力与实际不符。

(2)利用“两状态对比法”分析了地表超载作用下既有盾构隧道对地层的相对挤压作用，并结合模型试验测得土层沉降与隧道变形结果进行分析，推导得到了盾构隧道对周围土体相对挤压量的计算公式，为下一步分析地表超载作用下既有盾构隧道附加土压力解析计算奠定了基础。

(3)地表超载作用下，盾构隧道对其侧部土体的水平相对挤压量与隧道变形有关，水平相对挤压量可近似简化为三角形，相对挤压的作用范围(也即水平地层抗力的作用范围)约为72°。

(4)地表超载作用下，当隧道穿越土层的竖向压缩量大于隧道的竖向收敛变形时，隧道对地层产生竖向相对挤压。竖向相对挤压量与隧道变形及穿越土层的压缩模量有关。