三视图确定的几何体唯一吗?

广东省深圳市光明新区高级中学(518106) 姜 玮

一、一道错题的分析

在刚刚出炉的2018年普通高等学校招生全国统一考试大纲(理科数学)的第II部分中,对立体几何部分有下列要求:能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型[1].文科数学也有同样的要求.可见由三视图确定几何体是立体几何部分的重点考查内容之一.

而在人教A版必修2教科书上1.2.2《空间几何体的三视图》一节的课后练习2则是这样一道题“观察下列几何体的三视图,想象并说出它们的几何结构特征,然后画出它们的示意图”[2].由于此题中三视图对应的空间几何体都是唯一的,且课本中对于三视图对应的空间几何体是否唯一也没有给出一般性的结论,因此学生很容易根据经验认为三视图可以确定唯一的空间几何体.

然而,三视图真的能唯一确定空间几何体吗?

在河南省洛阳市2016—2017学年高中三年级期中考试有这样一道数学题:一个几何体的三视图都是边长为1的正方形,如图1,则该几何体的体积是()

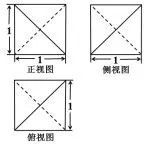
图1

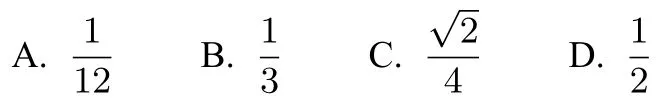
解法一该三视图对应的几何体是如图2所示三棱锥A1−BC1D.三棱锥A1−BC1D可以看成正方体截去四个角,即截去三棱锥A−A1BD,C−C1BD,B1−A1BC1,D1−A1DC1后剩下的多面体.这四个三棱锥都是同底等高的.因此这也是该题参考答案给出的正确选项B的由来.

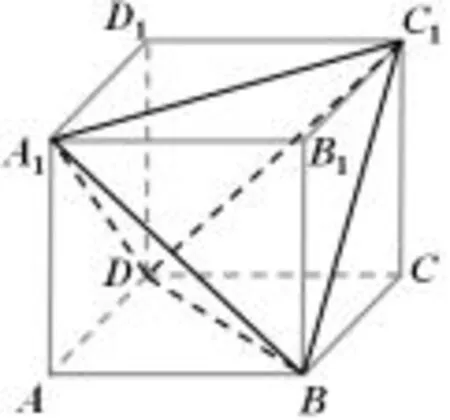
图2

图3

解法二然而通过观察我们发现,如图3所示多面体A1B1C1BD——即正方体截去三棱锥A−A1BD,C−C1BD,D1−A1DC1后剩下的多面体,其三视图也与图1一模一样.则此时那么这道题的选项D也是正确的.

所以我们不难发现,这道题如果作为一道单选题实际上是一道错题,该题的错误正是在于题目所给的三视图对应的空间几何体并不唯一.除了正方体截去四个角后剩下的三棱锥A1−BC1D三视图符合图1,该正方体截去上述四个角中的任意三个后形成的多面体的三视图也符合图1.这样的截法有四种,也就意味着至少有五种几何体可以对应图1中的三视图.

如果命题人意识到上述问题,就会知道要使本题中三视图所对应的空间几何体唯一,则必须加上更细致的要求.比如将题目中的“几何体”改为“三棱锥”,方可保证该题作为单选题的正确性.

二、一个实例的深化

有些同学可能会怀疑,是否因为本题过于特殊,才导致了几何体不唯一呢?下面我们以常见的正方体组合体为例,来进一步说明三视图所对应的几何体不一定是唯一的.

如图4所示,该几何体由8个棱长为1正方体组合而成,这个组合体的三视图如图5所示.

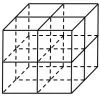
图4

图5

但是该组合体去掉任意一个小正方体后(如图6),三视图还是与图5相同,还可以按照图7去掉两个小正方体,三视图也仍然不变.甚至我们可以发现,最少仅需4个正方体(如图8),就可以保证其三视图与图5相同!

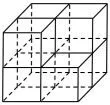
图6

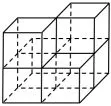
图7

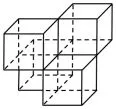
图8

由此可见,三视图对应的几何体确实是不唯一的.

因此,作为教师在出题时一定要考虑题目的严谨性与科学性.本例图5中三视图对应的组合体不仅不唯一,而且有很多不同情况.如果考察原几何体的体积或表面积势必会有多种不同的答案,因此可以改为通过排列组合的方法考察学生对该三视图对应的组合体的多样性的认识.

例1 某空间几何体由若干个棱长为1正方体组合而成,其三视图如图5所示,试问这样的几何体有多少个?

解答要组成该几何体最少只需要4个小立方体,最多需要8个,因此可以按小立方体的个数进行分类.

4个小立方体时,上下两层每层一个,且同层两个不在同一排或一列.上层两个方块一旦确定位置,下层两个方块的位置也会对应确定,因此有2种排列方法.

5个小立方体时,可以看成4个能确定该三视图的小立方体加上任意1个小立方体.除去已确定的四个小立方体,还有4个空位,而4个小立方体一共有两种排列方式能满足该三视图,因此共有种排列方式.

6个小立方体时,可以看成8个立方体减去2个小立方体,但是减去的两个小立方体不能在大正方体的同一条棱上,因此共有种排列方法.

7个小立方体时,可以看成8个立方体减去任意1个小立方体,因此共有种排列方法.

8个小立方体时,只有如图4唯一一种排列方法.

因此共有2+8+16+8+1=35种排列方法使若干个棱长为1的小立方体组成的几何体三视图如图5所示.