2018年美国数学竞赛(AMC12A)的试题与详细解答
广东省华南师范大学数学科学学院(510631) 李湖南
1.A large urn contains 100 balls,of which 36%are red and the rest are blue.How many of the blue balls must be removed so that the percentage of red balls in the urn will be 72%?(No red balls are to be removed.)
(A)28 (B)32 (C)36 (D)50 (E)64
译文 一个大缸里有100个球,其中36%是红球,其余的是蓝球.问要拿走多少个蓝球才能使大缸里红球的比例是72%(不拿走红球)?
解红球有100×36%=36个,拿走蓝球数为100−36÷72%=50个,故(D)正确.
2.While exploring a cave,Carl comes across a collection of 5-pound rocks worth$14 each,4-pound rocks worth$11 each,and 1-pound rocks worth$2 each.There are at least 20 of each size.He can carry at most 18 pounds.What is the maximum value,in dollars,of the rocks he can carry out of the cave?
(A)48 (B)49 (C)50 (D)51 (E)52
译文 一个岩洞爆破过后,卡尔发现一大堆岩石,每块5磅的岩石价值14美元,每块4磅的岩石价值11美元,每块1磅的岩石价值2美元.每种型号的岩石都至少有20块.卡尔至多能带走18磅岩石.问他能带走最多价值多少美元的岩石离开岩洞?
解很明显,为了价值最大,卡尔要带走尽可能多的4磅或5磅的岩石.实际上,他带走2块4磅的和2块5磅的岩石,价值最大,为2×14+2×11=50美元,故(C)正确.
3.How many ways can a student schedule 3 mathematics courses—algebra,geometry,and number theory—in a 6-period dayifnotwomathematicscoursescanbetakeninconsecutiveperiods?(What courses the student takes during the other 3 periods is of no concern here.)
(A)3 (B)6 (C)12 (D)18 (E)24
译文 如果一个学生一天上6节课,任意两节数学课不相连,问一个学生有多少种方法安排他的3节数学课—代数、几何和数论?(其它3节课是什么课与此无关)
解要使得任意两节数学课不相连,只能将3节数学课安排在第 1、3、5 节,或第 1、3、6 节,或第 1、4、6 节,或第 2、4、6节,共4种可能,而每一种可能,都有3!=6种方法,因此共有24种方法,故(E)正确.
4.Alice,Bob and Charlie were on a hike and were wondering how far away the nearest town was.When Alice said,“We are at least 6 miles away,”Bob replied,“We are at most 5 miles away.”Charlie then remarked,“Actually the nearest town is at most 4 miles away.”It turned out that none of the three statements was true.Letdbe the distance in miles to the nearest town.Which of the following intervals is the set of all possible values ofd?
(A)(0,4) (B)(4,5) (C)(4,6) (D)(5,6) (E)(5,∞)
译文 艾莉丝、鲍勃和查理在徒步旅行,他们想知道他们离最近的镇有多远.艾莉丝说:“我们至少有6英里远.”鲍勃说:“我们至多有5英里远.”查理说:“实际上最近的镇至多还有4英里远.”事实证明三个人说的都不对.设是他们到最近的镇的距离,下列哪个区间是d可能的取值?
解艾莉丝说的不对说明d不到6英里,鲍勃和查理说的也不对说明d超过5英里,即d应该在5英里到6英里之间,故(D)正确.
5.What is the sum of all possible values ofkfor which the polynomialsx2−3x+2andx2−5x+khavearootincommon?
(A)3 (B)4 (C)5 (D)6 (E)10
译文 多项式x2−3x+2和x2−5x+k有一个公共根,则k的所有可能取值的和是多少?
解多项式x2−3x+2的根为1和2,代入x2−5x+k得k=4或k=6,故(E)正确.
6.For positive integersmandnsuch thatm+10<n+1,both the mean and the median of the set{m,m+4,m+10,n+1,n+2,2n}are equal ton.What ism+n?
(A)20 (B)21 (C)22 (D)23 (E)24
译文 已知m和n是正整数,且m+10<n+1,集合{m,m+4,m+10,n+1,n+2,2n}的平均数和中位数均等于n,问m+n是多少?
解中位数为平均数为解得于是m+n=21,故(B)正确.
7.For how many(not necessarily positive)integer values ofnis the value of 4000an integer?
(A)3 (B)4 (C)6 (D)8 (E)9
译文 有多少个整数n(不必是正的)可以使得的值是一个整数?
解当n≥0时,是整数,则n=0,1,2,3;当n<0时,是整数,则n=−1,−2,−3,−4,−5.因此n共有 9个取值,故(E)正确.
8.All of the triangles in the diagram below are similar to isosceles triangleABC,in whichAB=AC.Eachofthe7smallesttriangleshasarea 1,and△ABChas area 40. What is the area of trapezoidDBCE?

图1
(A)16 (B)18 (C)20 (D)22 (E)24
译文 如图1,所有的三角形都相似于等腰三角形ABC,其中AB=AC,7个小三角形的面积均为1,三角形ABC的面积为40,则梯形DBCE的面积是多少?
解分别延长小三角形的腰线,可得图2.易得所有小三角形均全等,面积均为1,因此三角形ADE的面积为1+3+5+7=16,梯形DBCE的面积=40−16=24,故(E)正确.
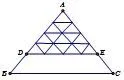
图2
9.Whichofthefollowingdescribesthelargestsubsetofvalues ofywithin the closed interval[0,π]for which sin(x+y)≤sinx+sinyfor everyxbetween 0 andπ,inclusive?

译文 下列哪个区间是y值在闭区间[0,π]上的最大子集,使得式子sin(x+y)≤sinx+siny对所有的0≤x≤π成立?
解当0≤x,y≤π时,sinx≥0,siny≥0,于是有sin(x+y)=sinxcosy+cosxsiny≤sinx+siny,区间内的一切y值均满足,故(E)正确.
10.How many ordered pairs of real numbers(x,y)satisfy the following system of equations
(A)1 (B)2 (C)3 (D)4 (E)8
译文 有多少对有序实数对(x,y)满足以下方程组
解先去绝对值符号,||x|−|y||可得四种结果:x−y,x+y,−x−y,−x+y,代入后分别与x+3y=3联立方程组,解得三组解:经检验,它们均为原方程组的解,故(C)正确.
11.A paper triangle with sides of lengths 3,4 and 5 inches,as shown,is folded so that point A falls on point B.What is the length in inches of the crease?

译文 一张三角形纸的三边长分别为3,4,5英寸,如图3,现将纸折叠使得点A落到点B上,问折痕的长度是多少英寸?
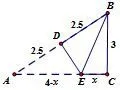
图3
解如图3,设折痕为DE,则AD=DB=2.5,令EC=x,则AE=BE=4−x,由勾股定理可得:(4−x)2=x2+32,解得故(D)正确.
12.LetSbe a set of 6 integers taken from{1,2,…,12}with the property that ifaandbare elements ofSwitha<b,thenbis not a multiple ofa.What is the least possible value of an element ofS?
(A)2 (B)3 (C)4 (D)5 (E)7
译文 设S是一个从{1,2,…,12}中取出的6个元素的集合,具有以下性质:若a和b均是S中的元素,且a<b,则b不是a的倍数.问S中元素的最小可能取值是多少?
解这个性质说明:集合S中的元素不存在倍数关系.显然,S中最小元素不能是1;若S中最小元素为2,则S={2,3,5,7,9,11},元素3和9不符合性质,矛盾!若S中最小元素为3,则S⊆{3,4,5,7,8,10,11},元素4和8、5和10均不符,矛盾!因此,S中可能的最小元素是4,此时S={4,5,6,7,9,11}或S={4,6,7,9,10,11}均满足要求,故(C)正确.
13.How many nonnegative integers can be written in the forma7·37+a6·36+a5·35+a4·34+a3·33+a2·32+a1·31+a0·30,whereai∈{−1,0,1}for 0≤i≤ 7?
(A)512 (B)729 (C)1094 (D)3281 (E)59,048
译文 有多少个非负整数可以写成如下形式:a7·37+a6·36+a5·35+a4·34+a3·33+a2·32+a1·31+a0·30,其中ai∈{−1,0,1},0≤i≤7?
解由于 3n>3n−1+3n−2+···+31+30,n是正整数,所以当以上3的多项式中首项系数an,0≤n≤7取 1的时候,其它的系数ai,i=0,1,···,n−1可以任意取,显然首项系数不能取−1,因此所有可能的组合有37+36+35+34+33+32+31+30+1=3281种,故(D)正确.
14.The solutions to the equation log3x4=log2x8,wherexis a positive real number other thancan be written aswherepandqare relatively prime positive integers.What isp+q?
(A)5 (B)13 (C)17 (D)31 (E)35
译文 设x是不等于的正实数,方程log3x4=log2x8的解可以写成其中p和q是互素的正整数,问p+q是多少?
解由换底公式可得化简成解得故(D)正确.
15.A scanning code consists of a 7×7 grid of squares,with some of its squares colored black and the rest colored white.There must be at least one square of each color in this grid of 49 squares.A scanning code is called symmetric if its look does not change when the entire square is rotated by a multiple of 90°counterclockwisearounditscenter,norwhenitisreflectedacross a line joining opposite corners or a line joining midpoints of opposite sides.What is the total number of possible symmetric scanning codes?
(A)510 (B)1022 (C)8190 (D)8192 (E)65,534
译文 一个扫描码包含一个7×7正方形方格,其中一些方格是黑色的,而其余的是白色.在这49个方格中,每种颜色必须至少有一格.如果一个扫描码围绕着它的中心做90°的整数倍的逆时针旋转还是一样的,或者沿着对角线或对边中点连线的翻转也不变,则称这个扫描码是对称的.问对称的扫描码共有多少个?
解由于对称的扫描码绕着中心90°旋转是一样的,从而只需要考虑左上角的4×4正方形方格即可;又由于该4×4的正方形方格关于对角线对称,所以只需考虑图4中标有a,b,c,d,e,f,g,h,i,j的10个方格即可,每个方格的颜色有黑色和白色2种选择,故有210=1024种,再减去全黑和全白的2种,共有1022种,故(B)正确.
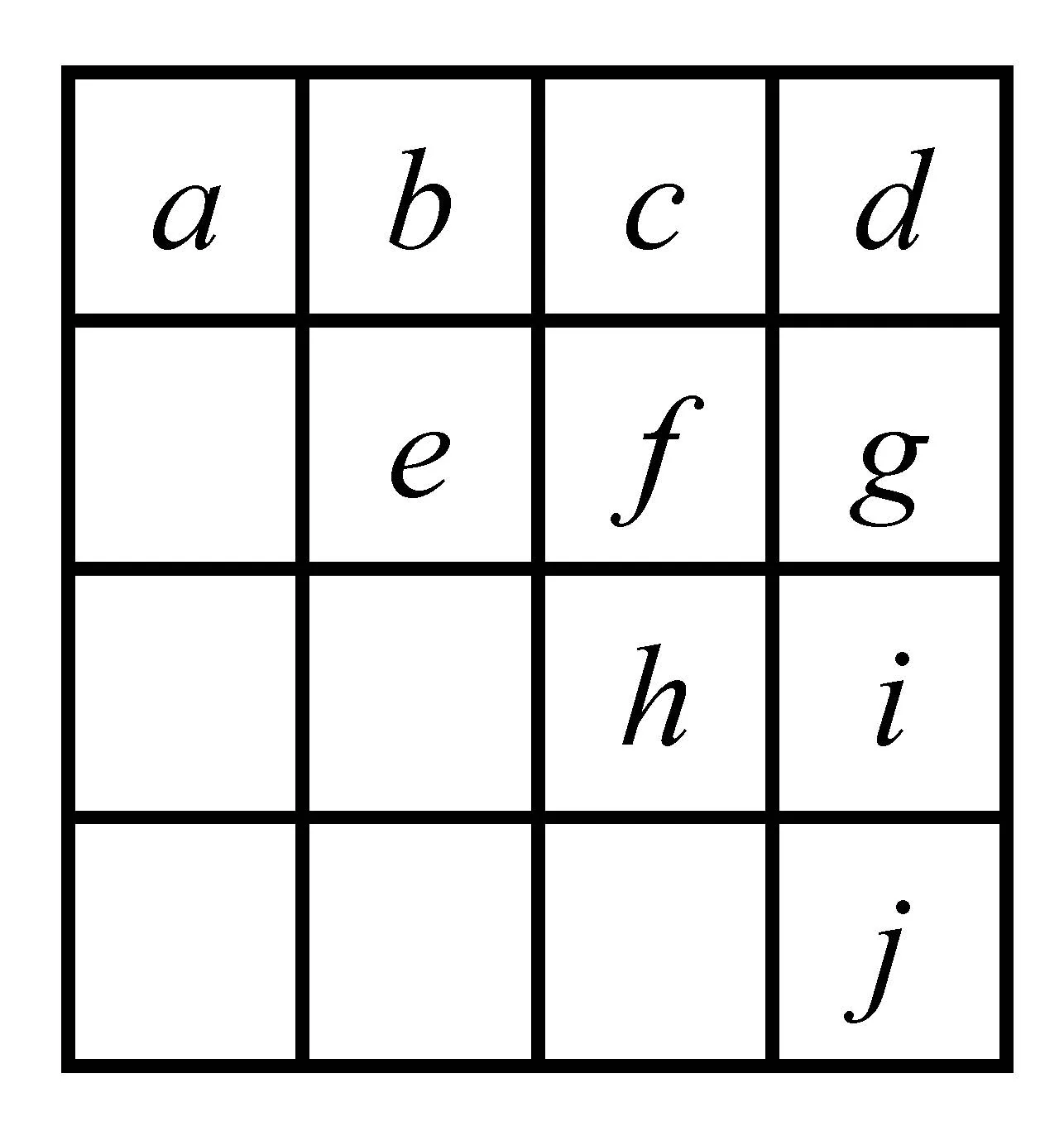
图4
16.Which of the following describes the set of values ofafor which the curvesx2+y2=a2andy=x2−ain the realxy-plane intersect at exactly 3 points?

译文a取何值时,曲线x2+y2=a2与y=x2−a在实平面上恰好有3个交点?
解代入可得x2+(x2−a)2=a2,化简得x2(x2−2a+1)=0,要使得该方程有3个不同的解,则x2−2a+1=0必须有2个解,即有x2=2a−1>0,于是故(E)正确.

图5
17. Farmer Pythagoras has a field in the shape of a right triangle.The right triangle’s legs have lengths of 3 and 4 units.In the corner where those sides meet at a right angle,he leaves a small unplanted squareSso that from the air it looks like the right angle symbol.The rest of the field is planted.The shortest distance fromSto the hypotenuse is 2 units.What fraction of the field is planted?

译文 农夫毕达哥拉斯有一块直角三角形的地,直角边长分别为3个单位和4个单位.在构成直角的那个角落里,他留了一小块未种植的正方形地S,从空中看上去就像一个直角符号.其余的地均进行了种植.S到斜边的最短距离是2个单位.问种植的地占多少比例?

图6
解如图6,分别延长ED、FD交AC于点L、K,作LH⊥BC于H,设正方形边长为x个单位,则由于△KDL~=△ABC,可以设KD=3k,DL=4k,于是解得因为解得则S占地比例为因此所求的占地比例为故(D)正确.
18.TriangleABCwithAB=50 andAC=10 has area 120.LetDbe the midpoint ofAB,and letEbe the midpoint ofAC.The angle bisector of∠BACintersectsDEandBCatFandG,respectively.What is the area of quadrilateralFDBG?
(A)60 (B)65 (C)70 (D)75 (E)80
译文 三角形ABC的面积为120,AB=50,AC=10,D是AB的中点,E是AC的中点,∠BAC的平分线分别交DE和BC于F和G.求四边形FDBG的面积是多少?

图7
解如图7示,DE是△ABC的中位线,根据角平分线定理,从而可得而于是SFDBG=100−25=75,故(D)正确.
19.LetAbe the set of positive integers that have no prime factors other than 2,3,or 5.The infinite sumof the reciprocals of the elements ofAcan be expressed aswheremandnare relatively prime positive integers.What ism+n?
(A)16 (B)17 (C)19 (D)23 (E)36
译文 设A是不含除2,3或5外的素因子的正整数集合,A中元素的倒数之和可以表示成其中m和n是互素的正整数,问m+n是多少?
解由题目条件,可得
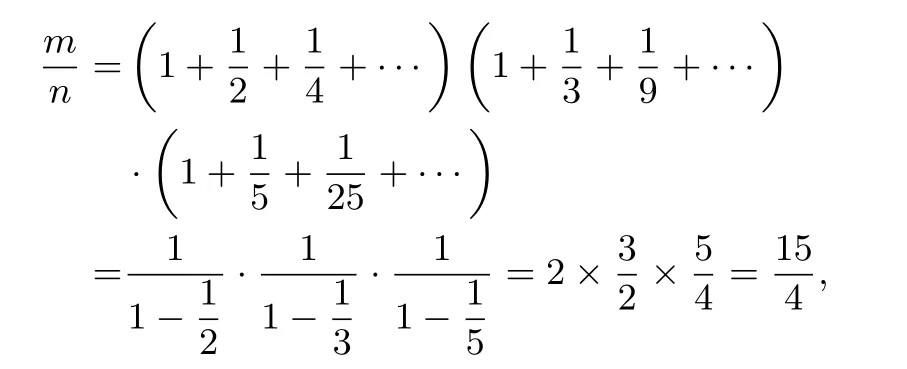
m+n=19,故(C)正确.
20.TriangleABCis an isosceles right triangle withAB=AC=3.Let M be the midpoint of hypotenuseBC.Points I and E lie on sidesACandAB,respectively,so thatAI>AEandAIMEis a cyclic quadrilateral.Given that triangleEMIhas area 2,the length CI can be written aswherea,bandcare positive integers andbis not divisible by the square of any prime.What is the value ofa+b+c?
(A)9 (B)10 (C)11 (D)12 (E)13
译文 三角形ABC是一个等腰直角三角形,AB=AC=3.M是斜边BC上的中点.点I和E分别在边AC和AB上,使得AI>AE,且AIME是一个圆内接四边形.设三角形EMI的面积为2,CI的长度可以写成其中a,b,c是正整数,且b不含素因子的平方,问a+b+c是多少?

图8
解如图8所示,连结AM,由四点共圆,可得∠EMI=90°,∠EIM=∠EAM=45°,从而△EMI也是等腰直角三角形,得MI=2,而根据余弦定理,MI2=MC2+CI2−2MC·CIcos∠C,代入 后得解得于是a+b+c=12,故(D)正确.
21.Which is the following polynomials has the greatest real root?
(A)x19+2018x11+1 (B)x17+2018x11+1
(C)x19+2018x13+1 (D)x17+2018x13+1
(E)2019x+2018
译文 下列哪个多项式的实根最大?
解容易分析这些多项式均是单调递增的.对于多项式f(x)=x2m+1+2018x2n+1+1,m,n为自然数,当x≤−1时,有f(x)<0;当x≥0时,有f(x)>0,故f(x)的根一定在区间(−1,0)内.当x∈(−1,0)时,有x11<x13<x17<x19,这表明在前四个选项中,x17+2018x11+1的值最小,x19+2018x13+1的值最大.因此,x17+2018x11+1的根最大.另外,2019x+2018的根为而可知x17+2018x11+1的根大于x0,故(B)正确.
22.The solutions to the equationsandform the vertices of a parallelogram in the complex plane.The area of this parallelogram can be written in the formwherep,q,randsare positive integers and neitherqnorsis divisible by the square of any prime number.What isp+q+r+s?
(A)20 (B)21 (C)22 (D)23 (E)24
解解方程得解方程得z=则平行四边形的顶点坐标分别为O为两条对角线交点,可得OA= 4,OB= 2,由余弦定理,进而于是故(A)正确.

图9
23. In△PAT,∠P=36°,∠A=56°,andPA=10.PointsUandGlie on sidesTPandTA,respectively,so thatPU=AG=1.LetMandNbe the midpoints of segmentsPAandUG,respectively.What is the degree measure of the acute angle formed by linesMNandPA?

图10
(A)76 (B)77 (C)78 (D)79 (E)80
译文 在△PAT中,∠P=36°,∠A=56°,PA=10.点U和G分别在边TP和TA上,使得PU=AG=1.设M和N分别是PA和UG的中点.问直线MN和PA所夹的锐角是多少度?
解如图所示,以P为原点,PA为x轴建立直角坐标系,则有点坐标M(5,0),U(cos36°,sin36°),G(10−cos56°,sin56°),从而
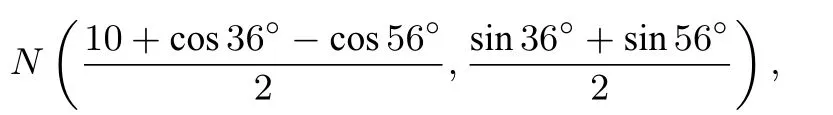
所求的锐角为∠NMA,于是

因此∠NMA=80°,故(E)正确.
24.Alice,Bob and Carol play a game in which each of them chooses a real number between 0 and 1.The winner of the game is the one whose number is between the numbers chosen by the other two players.Alice announces that she will choose her number uniformly at random from all the numbers between 0 and 1,and Bob announces that he will choose his number uniformly at random from all the numbers betweenArmed with this information,what number should Carol choose to maximize her chance of winning?

译文 艾莉丝、鲍勃和卡罗尔在玩一种游戏,每个人在0和1之间选一个实数,谁的数在其他两人之间谁就赢了.艾莉丝宣布她会在0和1之间随机选一个数,鲍勃宣布他会在之间随机选一个数.有了这些信息,卡罗尔应该选什么数才能使他赢的机会最大?
解设艾莉丝选的数为x,x∈[0,1],鲍勃选的数为y,卡罗尔选的数为z,z∈[0,1],于是P(x<z)=z,P(z<x)=1−z,卡罗尔赢的两种情况为:(1)当x<z<y时:概率为当y<z<x时:概率为因此卡罗尔赢的概率为时,概率最大为故(B)正确.
25.For a positive integernand nonzero digitsa,bandc,letAnbe then-digit integer each of whose digits is equal toa;letBnbe then-digit integer each of whose digits is equal tob;and letCnbe the 2n-digit(notn-digit)integer each of whose digits is equal toc.What is the greatest possible value ofa+b+cfor whichthereareatleasttwovaluesofnsuchthatCn−Bn=A2n?
(A)12 (B)14 (C)16 (D)18 (E)20
译文 已知n是正整数,a,b,c是非零数字,设An是数字均为a的n位数,Bn是数字均为b的n位数,Cn是数字均为c的2n位数(不是n位).求a+b+c可能取到的最大值,使得至少存在两个n值能让等式Cn−Bn=A2n成立?

即c·(10n+1)=b+a2·进一步可得
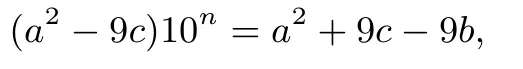
由于至少存在两个n值使该式成立,所以解得.因此a+b+c的最大值等于18,故(D)正确.

