关于一道高考题的思考

陈飞龙

（合肥市第七中学，安徽 合肥）

首先我们来看看原题和给出的参考答案：

25.（20分）如图，两水平面（虚线）之间的距离为H，其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和-q（q＞0）的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域，并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下；M在电场中做直线运动，刚离开电场时的动能为N刚离开电场时动能的1.5倍。不计空气阻力，重力加速度大小为g。求

（1）M与N在电场中沿水平方向的位移之比；

（2）A点距电场上边界的高度；

（3）该电场的电场强度大小。

看到这一题参考答案的解法（此处略去），很多学生感到思维连贯性不强，也就是感到物理过程理解不透彻，即是说看着答案我能把每步骤看懂，但是自己去解题的过程中可能不知道要这么入手，笔者在求解本题的过程中使用的方法与参考答案有些区别，现供读者参考。

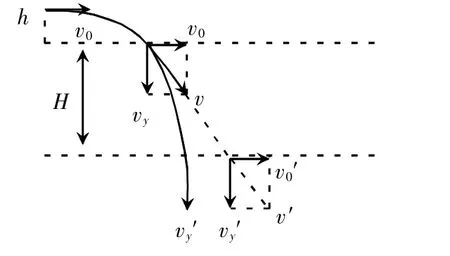
方法一：

（1）进入电场后，M、N水平方向做匀加速，竖直方向也做匀加速直线运动，水平和竖直具有等时性：

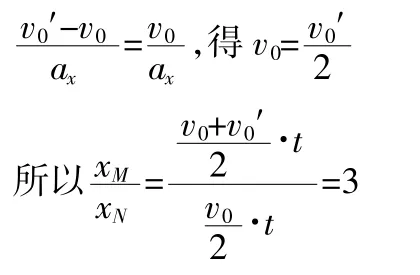
（2）由上问知 v0′=2v0，vy′=2vy，v′=2v

利用竖直方向匀加速得：

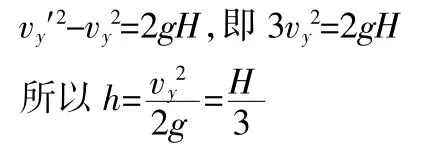
这种方法的优点在于先指出M刚进入电场和刚离开电场之间速度的2倍比例关系，由此来进行计算和分析较直观和方便。

方法二：

对于本题的求解，我们也可使用动量定理：

（1）对M、N的水平方向分别应用动量定理得

-Eq·Δt=0-mv0

Eq·Δt=mv0′-mv0

于是得：v0=v0′-v0，即 v0′=2v0

由此知 vy′=2vy，v′=2v

（2）对M的水平和竖直方向分别应用动量定理得：（Δt为在电场中的时间）

Eq·Δt=m（v0′-v0）

mg·Δt=m（vy′-vy）

两式相比可得：

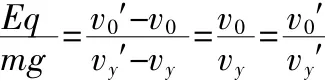
（3）由 Eq·Δt=m（vy′-vy），vy′=2vy，得 vy=g·Δt，于是知道平抛运动的时间与在电场中的时间相同。

再由竖直方向自由落体的规律知：

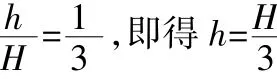
本题的几种求解方法各有不同之处，参考答案上侧重于直接使用运动学公式和动能定理，直来直去，需要对题目有较深的理解和运算能力，笔者给出的两种解法主要把握住水平和竖直两方向的分别分析，强调两方向的运动等时性，并注意M出电场和入电场时合速度和各分速度的比值关系，从而可适当降低运算量以利于学生理解。