Hilbert 空间等价类的万有右稳定性
卫 倩, 夏红川
(信阳师范学院 数学与统计学院,河南 信阳 464000)
0 引言
有关Banach空间中等距和ε-等距性质的研究已有80多年历史.1932年,波兰数学家MAZUR和ULAM[1]首先研究了满等距映射,并给出一个优美的结果:若f:X→Y是满等距且f(0)=0,则f是线性的.这说明Banach空间的度量结构完全决定了空间的线性结构.MAZUR和ULAM对满等距问题的证明使得数学家们开始关注ε-等距性质的研究.1945年,HYERS和ULAM[2]研究了满ε-等距,并提出问题:设X和Y是Banach空间,对于任意的标准满ε-等距f:X→Y,是否存在γ>0及线性等距U:X→Y,使得f-U在X上有一致上界γε.经过数学家们半个世纪的努力,OMLADI和EMRL[3]在1995年给出了Hyers-Ulam问题具有最优估计值的肯定回答.1968年,FIGIEl[4]研究了非满等距,并证明了对于任一标准等距f:X→Y,存在模为1的线性左逆算子.关于Hyers-Ulam问题和著名的Figiel定理,QIAN[5]于1995年首次提出下面的问题:是否对于每一对Banach空间(X,Y),均存在α>0和γ>0,使得任意的标准ε-等距f:X→Y是(α,γ)稳定的?
对于非满ε-等距稳定性的研究是困难和复杂的.当Banach空间X和Y是Lp空间时,QIAN[5]、EMRL和VISL[6]给出了上述问题的肯定回答.但在一般情形下,QIAN[5]的反例表明此结论不成立.2013年,CHENG等[7]给出了Banach空间中非满ε-等距的弱稳定性描述.随后,他们[8]又给出了弱稳定性公式中的最优估计值.
Banach空间上ε-等距的稳定性得到了学者们的进一步研究[9-13],下列问题在文献[9,10]中曾被提出:
问题1 是否存在一类Banach空间X满足任意给定X∈X和任意Banach空间Y,(X,Y)是稳定的?其中X中的任一Banach空间X称为万有左稳定的.
问题2 是否存在一类Banach空间Y满足任意给定Y∈Y和任意Banach空间X,(X,Y)是稳定的?其中Y中的任一Banach空间Y称为万有右稳定的.
近年来,CHENG等[9,10]系统地研究了Banach空间的万有左稳定性和万有右稳定性,证明了:每一个λ单空间是万有左稳定的;线性同构于l的一个无限维子空间的Banach空间X是万有左稳定的当且仅当X同构于l;可分Banach空间X满足对于任意可分Banach空间Y,(X,Y)是稳定的当且仅当X同构于c0;Banach空间X是万有左稳定的当且仅当X是势单空间;若Banach空间Y是万有右稳定的,则Y同构于Hilbert空间.
本文将进一步研究同构于Hilbert空间的Banach空间Y是万有右稳定时所具有的性质.结果表明:当Banach空间Y同构于一Hilbert空间时,Y是万有右稳定的当且仅当对任一可分Banach空间X,(X,Y)是稳定的.
1 Hilbert空间等价类的万有右稳定性
定义1[5]设X和Y是Banach空间,ε≥0,f:X→Y是标准的ε-等距.称f是(α,γ)稳定的,如果存在α>0和γ>0,以及有界线性算子

且‖T‖≤α,使得
‖Tf(x)-x‖≤γε,∀x∈X.
在不引起混淆的情况下,也简单地说f是稳定的.
定义2[5]称一对Banach空间(X,Y)是稳定的,如果对于任意标准的ε-等距f:X→Y,存在α>0和γ>0,使得f是稳定的.
定义3[10]称Banach空间X(Y)是万有左(右)稳定的,如果任给Banach空间Y(X),(X,Y)是稳定的.
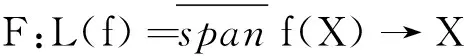
引理2[8]设X和Y是Banach空间,映射f:X→Y是标准的ε-等距,则对于任意的x*∈X*,存在φ∈Y*且
‖φ‖=‖x*‖=r,
使得
|〈φ,f(x)〉-〈x*,x〉|≤2rε,∀x∈X.
(1)
引理3 设X和Y是Banach空间,Y同构于一Hilbert空间,映射f:X→Y是标准的ε-等距.任意给定N上的自由超滤子U,则由
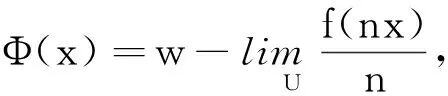
(2)
定义的映射Φ:X→Y满足:
(1)Φ(0)=0,
(2)‖Φ(x)-Φ(y)‖=‖x-y‖,对任意的x,y∈X,Y赋予弱拓扑.
证明因为Banach空间Y同构于一Hilbert空间,所以Y是自反的.任意给定x∈X,

(1)Φ(0)=0显然成立.
(2)一方面,对任意的x,y∈X,有
‖Φ(x)-Φ(y)‖=
(3)
另一方面,任取x,y∈X,由Hahn-Banach定理知,存在x*∈SX*,使得
〈x*,x-y〉=‖x-y‖.
由引理2知,存在φ∈SY*,使得
|〈φ,f(x)〉-〈x*,x〉|≤2ε,
则
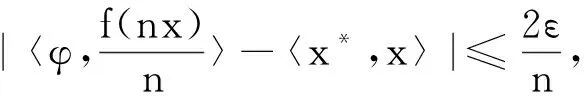
且
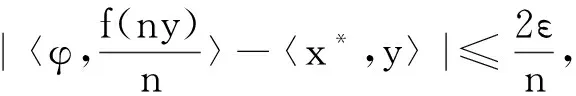
因此
‖x-y‖=〈x*,x-y〉=
〈φ,Φ(x)-Φ(y)〉≤
‖Φ(x)-Φ(y)‖.
(4)
由式(3)和式(4)即得
‖Φ(x)-Φ(y)‖=‖x-y‖,∀x,y∈X.
证毕.
引理3说明了映射Φ:X→Y是标准等距.下面考虑Hilbert空间等价类的闭子空间的可补性以及可分子空间的稳定性.
引理4 若Banach空间Y同构于一Hilbert空间H,则Y的任一闭子空间是一致可补的.
证明记
β=dist(Y,H)=
inf{‖T-1‖‖T‖:T:Y→H是线性同构},
则存在线性同构T:Y→H,使得
任取闭子空间M⊂Y,则
T1=T|M:M→T(M)
是线性同构.因为闭子空间T(M)在H中是1-可补的,所以存在有界线性投影P1:H→T(M)且‖P1‖=1.
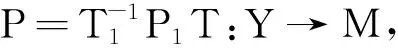
另一方面
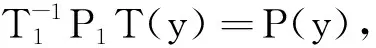
因此P:Y→M是线性投影且
‖P‖≤β+1.
由闭子空间M的任意性知,Banach空间Y是一致可补的,即Y的任一闭子空间是β+1可补的.证毕.
引理5 设X和Y是Banach空间,f:X→Y是标准的ε-等距.若对于任一可分子空间Xα⊂X,f|Xα是稳定的,则对于任意可分子空间,f是一致稳定的,即存在M>0,对于任意的可分子空间Xα⊂X,存在有界线性算子
Tα:L(f|Xα)→Xα,
使得对于任意的x∈Xα,
‖Tαf(x)-x‖ 证明任取可分子空间Xα⊂X.记Mα=inf{γα:存在有界线性算子 Tα:L(f|Xα)→Xα 及γα>0,使得对任意的x∈Xα都有 ‖Tαf(x)-x‖<γαε}. 因为f|Xα是稳定的,所以存在α0>0,γ0>0和有界线性算子Tα:L(f|Xα)→Xα且‖Tα‖≤α0,使得 ‖Tαf(x)-x‖≤γ0ε,∀x∈Xα. 因此Mα非空,且Mα<.令 则M<.否则,对任意n∈N,存在Mn,使得Mn>n.令 X 显然X是可分的,因此存在α1>0,γ1>0和有界线性算子 T:L(f|X)→X,‖T‖≤α1, 使得 ‖Tf(x)-x‖≤γ1ε,∀x∈X. 特别地, ‖Tf(x)-x‖≤γ1ε,∀x∈Xn,∀n∈N. 因此对于任意的n∈N,Mn≤γ1,取n=[γ1]+1,则Mn>n>γ1.矛盾. 于是,对于任意可分子空间Xα⊂X,存在有界线性算子Tα:L(f|Xα)→Xα,使得 ‖Tαf(x)-x‖ 即对于任意可分子空间,f是一致稳定的.证毕. CHENG等利用不变平均值方法研究了非满ε-等距的性质.有关半群中不变平均值的定义和相关结果,参照文献[14]. 定义4[14]设G是一个半群,称l(G)上的线性泛函μ是G上的左不变平均值,如果μ满足 (1)μ(1)=1, (2)μ(f)≥0,对任意的f∈l(G)且f≥0, (3)μ(fg)=μ(f),对任意的f∈l(G)和g∈G.其中fg是f对g的左变换,即fg(h)=f(gh),对任意的h∈G. 同样地,可以定义G上的右不变平均值.称μ是G上的不变平均值,如果μ既是左不变平均值又是右不变平均值. 引理6[14]每个Abel半群都有一个不变平均值. 现设X和Y是Banach空间,f:X→Y是标准的ε-等距.注意到X关于向量的加法是一个Abel半群,由引理6,存在l(X)上的不变平均值μ.因为f是标准的ε-等距,所以 gx(z)=f(x+z)-f(z),∀z∈X. 定义了一个有界映射gx:X→Y,因此, 〈φ,gx〉∈l(X),∀φ∈Y*. 记μz(·)是l(X)上的不变平均值,对x∈X定义映射R:Y*→RX为 〈Rφ,x〉=μz(〈φ,gx〉),∀φ∈Y*. 记N=kerR.CHENG和ZHOU利用不变平均值的方法得到了下面的结论. 引理7[15]设X和Y是Banach空间,映射f:X→Y是标准的ε-等距(ε≥0),则存在 N(=kerR)⊂Y*, 使得U:X*→Y*/N和V:Y*/N→X*是线性满等距且VU=IX*. 下面利用以上结论,给出Hilbert空间等价类是万有右稳定时所具有的性质. 定理1 设Banach空间Y同构于一Hilbert空间,则Y是万有右稳定的当且仅当对于任意可分的Banach空间X,(X,Y)是稳定的. 证明必要性显然成立,下面证明充分性.任意给定Banach空间X,设f:X→Y是标准ε-等距.由引理3知,由式(1)定义的Φ:X→Y是标准等距.根据引理1,存在有界线性算子 且‖F‖=1,使得F°Φ=IX. ‖TαPαf(x)-x‖≤γαδ,∀x∈Xα, 所以 TαPαΦ(x)=x,∀x∈Xα, 进而 TαPα|L(Φ|Xα)=F|L(Φ|Xα). 令T=F°P:Y→X.显然T是有界线性算子.对于任意的x∈Xα,有 ‖Tf(x)-x‖=‖FPf(x)-x‖= ‖TαPαPf(x)-x‖= ‖TαPαf(x)-x‖≤γαδ. 于是对任意的x∈X,存在可分子空间Xα⊂X,使得x∈Xα,且满足 ‖Tf(x)-x‖≤γαδ. 根据引理5,对于任意可分Banach空间,f是一致稳定的.所以存在M>0,使得 ‖Tf(x)-x‖≤Mδ. 因此,任意给定Banach空间X,(X,Y)是稳定的,即Banach空间Y是万有右稳定的.证毕. 通过构造标准等距,验证Hilbert空间等价类的闭子空间的一致可补性和可分子空间的一致稳定性,利用已有结果,证明了同构于Hilbert空间的Banach空间Y的万有右稳定性是由可分Banach空间X决定的.因此,接下来考虑Hilbert空间等价类的万有右稳定性时,只需考虑当Banach空间X可分时,(X,Y)的稳定性.这对进一步研究Hilbert空间等价类是否是万有右稳定的有着重要作用.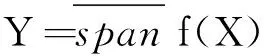
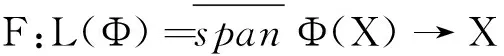
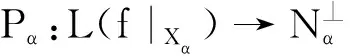
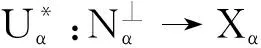

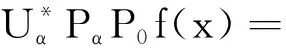
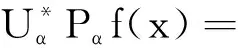
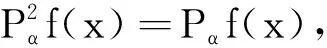
2 结语

